
CONTROLLING INVESTMENT PROPORTION IN CYCLIC
CHANGING ENVIRONMENTS
J.-Emeterio Navarro-Barrientos
Department of Computer Science, Humboldt-Universit¨at zu Berlin, Unter den Linden 6 10099, Berlin, Germany
Keywords:
Genetic algorithms, investment strategies, pattern recognition.
Abstract:
In this paper, we present an investment strategy to control investment proportions for environments with cyclic
changing returns on investment. For this, we consider an investment model where the agent decides at every
time step the proportion of wealth to invest in a risky asset, keeping the rest of the budget in a risk-free
asset. Every investment is evaluated in the market modeled by stylized returns on investment (RoI). For
comparison reasons, we present two reference strategies which represent agents with zero-knowledge and
complete-knowledge of the dynamics of the RoI, and we consider an investment strategy based on technical
analysis. To account for the performance of the strategies, we perform some computer experiments to calculate
the average budget that can be obtained over a certain number of time steps. To assure for fair comparisons,
we first tune the parameters of each strategy. Afterwards, we compare their performance for RoIs with fixed
periodicity (stationary scenario) and for RoIs with changing periodicities (non-stationary scenario).
1 INTRODUCTION
Finding a proper method to control investment pro-
portion is a problem that has been addressed by many
researchers (Kelly, 1956; Kahneman and Tversky,
1979). Many of the proposed methods are based on
machine learning (ML). For example, in (Magdon-
Ismail et al., 2001) the authors use neural networks
to find patterns in financial time series and in (Geibel
and Wysotzki, 2005), the authors propose a risk-
sensitive reinforcement learning algorithm to find
a policy for controlling under constraints. Other
techniques from ML that are also frequently used
are those based on evolutionary computation, like
genetic programming (GP) and genetic algorithms
(GA). For a general introduction to these techniques
for portfolio management and bankruptcy prediction
see (Dawid, 1999). Some researchers have shown that
investment strategies based on GP techniques may be
profitable; however, they usually find strategies which
can’t be easily funded (Schulenburg and Ross, 2001).
Controlling strategies that are based on a standard GA
may be also difficult to explain, however, we believe
that they are easier to understand than those using GP.
Genetic algorithms (GA) are stochastic search al-
gorithms based on evolution that explore progres-
sively from a large number of possible solutions find-
ing after some generations the best solution for the
problem. Inspired by natural selection, these powerful
techniques are based on some defined evolution oper-
ators, like selection, crossover and mutation (Holland,
1975). Moreover, some researches have extended
the use of GA for solving stochastic dynamic opti-
mization problems online (Grefenstette, 1992), where
most of the algorithms for changing environments are
tested in problems like the knapsack problem (Yang,
2005). However, to our knowledge, no-one has ap-
plied GAs specifically to the problem of controlling
the proportion of investment in environments with
cyclic changing returns on investment.
This paper is organized as follows: Sec. 2 de-
scribes the investment model and Sec. 3 presents
a novel approach to control investment proportions
based on a GA for environments with cyclic chang-
ing time series. In Sec. 4 we present the dynamics
for the risky asset and we compare the performance
of the adaptive strategy with other strategies for sta-
tionary and non-stationary environments.
2 INVESTMENT MODEL
We consider an investment model (Navarro and
Schweitzer, 2003) where an agent is characterized by
207
Navarro-Barrientos J. (2008).
CONTROLLING INVESTMENT PROPORTION IN CYCLIC CHANGING ENVIRONMENTS.
In Proceedings of the Fifth Inter national Conference on Informatics in Control, Automation and Robotics - ICSO, pages 207-213
DOI: 10.5220/0001496802070213
Copyright
c
SciTePress

two individual variables: (i) its budget x(t), and (ii) its
investment proportion q(t). The budget, x(t), changes
in the course of time t by means of the following dy-
namic:
x(t + 1) = x(t)
h
1+ r(t)q(t)
i
(1)
This means that the agent at time t invests a por-
tion q(t)x(t) of its total budget. And this investment
yields a gain or loss on the market, expressed by r(t),
the return on investment, RoI. Some authors assume
that returns are obtained by means of continuous dou-
ble auction mechanisms (LeBaron, 2001), however,
in this paper we consider that the returns are not be-
ing influenced by agent’s actions, this approach plays
a role in more physics-inspired investment models,
(Richmond, 2001; Navarro-Barrientos et al., 2008).
Since q(t) always represents a portion of the total bud-
get x(t), and it is bound to q(t) ∈ [0,1]. For complete-
ness, we assume that the minimal and maximal in-
vestment proportions are described by q
min
and q
max
,
respectively.
Thus, in this paper we present an adaptive strat-
egy to control proportions of investment, expressed
by a method to find the most proper q(t). We assume
a simple dynamic for the returns allowing us to focus
in the feedback of these market returns on the invest-
ment strategy (and not on the feedback of the strate-
gies on the market). Moreover, we assume that the
agent invests independently in the market, i.e. there is
no direct interaction with other agents.
3 ADAPTIVE INVESTMENT
STRATEGY
In this section, we present an adaptive investment
strategy based on a GA for controlling proportions
of investment in cyclic changing environments. For
simplicity, we call this strategy Genetic Algorithm for
Changing Environments (GACE), and we show on the
following the specifications for the GA.
3.1 Encoding Scheme
We consider a population of chromosomes j =
1,...,C, where each chromosome j has an array of
genes, g
jk
, where k = 0,...,G
j
− 1, and G
j
is the
length of the chromosome j. The length of a chro-
mosome is assumed to be in the range G
j
∈ (1, G
max
),
where G
max
is a parameter that specifies the maximal
allowed number of genes in a chromosome. The val-
ues of the genes could be binary, but for program-
ming reasons we use real values (Michalewic¸z, 1999).
Moreover, each chromosome j represents a set of pos-
sible strategies of an agent, where each g
jk
is an in-
vestment proportion.
3.2 Fitness Evaluation
Each chromosome j is evaluated after a given num-
ber of time steps by a fitness function f
j
(τ) defined as
follows:
f
j
(τ) =
G
j
−1
∑
k=0
r(t)g
jk
; k ≡ t mod G
j
, (2)
where τ is a further time scale in terms of genera-
tions. When a generation is completed, the chromo-
somes’ population is replaced by a new population of
better fitting chromosomes with the same population
size C. Since the fitness of a chromosome tends to be
maximized, negative r(t) should lead to small values
of g
jk
, and positive r(t) should lead to larger values
of g
jk
. Because of this, we consider the product of
r(t)g
jk
as a performance measure, which is in accor-
dance with our investment model, Eq. (1). Notewor-
thy, in this approach the GA tries to find the chromo-
somes leading to larger profits. A different approach
would be to implement a GA to find the chromosomes
that minimize the loss, in which case, we would have
a different fitness function. Note that we treat directly
returns on investment and not price movements, be-
cause our goal is to evaluate the fitness of the strate-
gies for the RoI and not the accuracy of the prediction
of the next RoI.
3.3 Selection of a New Population
If we assume that chromosomes have fixed length,
G
j
= G
max
, then the most proper number of time steps
that have to elapse in order to evaluate all chromo-
somes’ genes is t
eval
= G
max
. However, this previous
assumption corresponds to the ideal case where the
agent knows the periodicity of the returns and sets the
length of all chromosomes to this value. In this paper,
we assume that the agent doesn’t know neither the
periodicity nor the dynamics of the RoI. Thus, we
assume that the chromosomes have different length.
Different approaches may be proposed to know after
how many time steps a new generation of chromo-
somes should be obtained, however, we find that the
best approach was to choose the number of time steps
for evaluation accordingly to the length of the best
chromosome in the population.
3.3.1 Elitist and Tournament Selection
After calculating the fitness of each chromosome ac-
cording to Eq. (2), we first find the best chromosomes
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
208
from the current population by applying elitist selec-
tion, which copies directly the best s percentage to the
new population. Afterwards, a tournament selection
of size two is done by randomly choosing two pairs
of chromosomes from the current population and then
selecting from each pair the one with the higher fit-
ness. These two chromosomes are not simply trans-
ferred to the new population, but undergo a transfor-
mation based on the genetic operators’ crossover and
mutation.
3.3.2 Crossover and Mutation Operators
The limitations of conventional crossover in GA with
variable length has already been addressed by some
authors, where neural networks or hierarchical tree-
structures are used to determine which genes should
be exchanged between the chromosomes (Harvey,
1992). For simplicity, we propose a modification
of the standard GA crossover operator that better
suits our demands. Thus, we propose the use of
a crossover operator called Proportional Exchange
Crossover (PEC) operator, which randomly selects
the range of genetic information to be exchanged be-
tween two chromosomes and contracts(extends) the
genetic information from the largest(shortest) to the
shortest(largest) chromosome, respectively. Algo-
rithm 1 shows the PEC algorithm for all pair of
parent-chromosomes being selected via tournament
selection. Note that a chromosome j is saved in an
array with indexes in the range [0,..,G
j
− 1]. The
shortest and largest parent-chromosomes are denoted
by pa
s
with size G
s
and pa
l
with size G
l
, resp., and
R ∈ N is the size proportion between these two parent-
chromosomes. The cross-points for the shortest and
largest parent-chromosomes are denoted by cp
s
∈ N
and cp
l
∈ N, respectively. The breeding between the
two parent-chromosomes results in a short and a large
children-chromosomes denoted by ch
s
and ch
l
, re-
spectively.
Note, that different functions could be consid-
ered for the transformation of the genetic material be-
tween chromosomes with different length. For sim-
plicity, we consider in our implementation of the Al-
gorithm 1 in line 9 the function extend(pa,m,R) =
pa[m], which simple copies the genes from the short
parent-chromosome to the large child-chromosome;
and in line 13 the function contract(pa,m,R) =
1/R
∑
m+R
i=m
pa[i], which performs an average over the
genetic material.
Now, to make sure that a population with chromo-
somes of diverse lengths is present, we introduce a
mutation operator for the length of the chromosome.
For this, with probability p
l
a new length is drawn
randomly and the genetic information of the chro-
Algorithm 1: Proportional Exchange Crossover
(PEC) operator.
foreach pair of parent-chromosomes do1
create ch
s
and ch
l
with sizes G
s
and G
l
2
find the cross-points:3
cp
s
∼ U(0,G
s
− 1); cp
l
=
G
l
cp
s
G
s
determine size proportion: R = cp
l
/cp
s
4
with p = 0.5 choose side for crossover5
if crossover on the left side then6
extend genes from pa
s
to ch
l
:7
for m = 0 to cp
s
− 1 do
for n = 0 to R− 1 do8
ch
l
[m· R+ n] ←9
extend(pa
s
,m,R)
end10
end11
contract genes from pa
l
to ch
s
:12
foreach m = 0 to cp
s
− 1 do
ch
s
[m] ← contract(pa
l
,m,R)13
end14
else15
extend as in 9 but for m = cp
s
to G
s
− 116
contract as in 13 but for m = cp
s
to17
G
s
− 1
end18
copy remaining genes in pa
s
and pa
l
into19
same positions in ch
s
and ch
l
, respectively.
end20
mosome is proportionally scaled to the new length,
leading to a new enlarged or stretched chromosome.
The algorithm used for the mutation of the length of
the chromosome is based on the same principle as
the PEC operator. After the crossover and length-
mutation operators are applied, the typical gene-
mutation operator is applied. This means that with a
given mutation probability p
m
∈ U(0,1), a gene is to
be mutated by replacing its value by a random number
from a uniform distribution U(q
min
,q
max
).
3.3.3 Strategy Selection and Initialization
For every new generation, the agent takes the set of
strategies g
jk
from the chromosome j with the largest
fitness in the previous generation.
q(t) = g
lk
with l = arg max
j=1,..,C
f
j
; k ≡ t mod G
l
(3)
For the initialization, each g
jk
is assigned a ran-
dom value drawn from a Uniform distribution: g
jk
∼
U(q
min
,q
max
). And for the length of the chromo-
somes, each G
j
is initialized randomly from a Uni-
form distribution of integers: G
j
∼ (1,G
max
), where
G
max
is the maximal allowed chromosome length.
CONTROLLING INVESTMENT PROPORTION IN CYCLIC CHANGING ENVIRONMENTS
209
4 EXPERIMENTAL RESULTS
In this section, we present the environment for the
agent and we analyze the performance of the adaptive
strategy presented above.
4.1 Artificial Returns
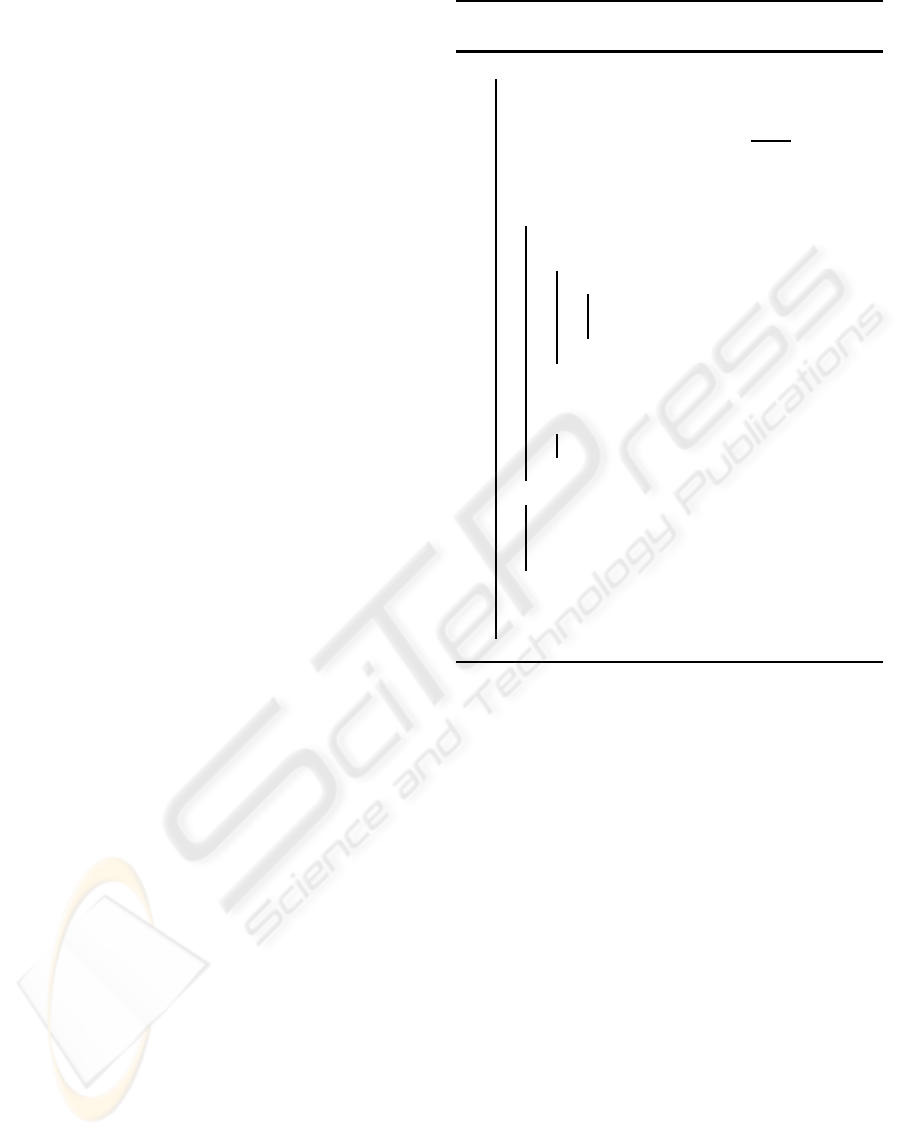
We consider artificially generated returns which are
driven by the following dynamics:
r(t) = (1− σ)sin
2π
T
t
+ σξ, (4)
where the amplitude of the returns depends on the am-
plitude noise level σ ∈ (0,1), and ξ corresponds to a
random number drawn from a Uniform distribution,
ξ ∈ U(−1,1). The periodicity of the returns is drawn
randomly T ∼ U(1, T
max
) and would be present for
a number of t
′
∼ U(1,t
max
) time steps. Thus, σ ac-
counts for the fluctuations in the market dynamics on
the amplitude of the RoI; T
max
accounts for the largest
possible periodicity and t
max
accounts for the max-
imal number of time steps a periodicity can elapse.
Fig. 1 shows an example of the RoI.
0 200 400 600 800 1000
t
-1
-0.5
0
0.5
1
r(t)
Figure 1: Periodic RoI, r(t), Eq. (4) for noise level σ = 0.1,
T
max
= 100 and t
max
= 1000.
4.2 Reference Strategies
For comparison purposes, we present in this section
different strategies which are used as a reference to
account for the performance of the adaptive strategy.
Note that we could have considered other type of
strategies which may lead to a more complete study.
However,our main goal is to show the performance of
GACE comparing it against the performance of other
strategies for the same investment scenario.
4.2.1 Strategies with Zero/Complete Knowledge
For comparison reasons, we present in this sec-
tion two strategies representing two simple behav-
iors for an agent: the first one, called Constant-
Investment-Proportion(CP), represents the agent with
zero knowledge and zero-intelligence; the second
one, called Square-Wave (SW), represents the agent
with complete knowledge of the environment.
Constant Investment Proportion (CP). The sim-
plest strategy for an agent would be to take a constant
investment proportion for every time step:
q(t) = q
min
= const. (5)
Square Wave Strategy (SW). An agent using this
strategy invests q
max
during the positive cycle of the
periodic return and invests q
min
otherwise:
q(t) =
(
q
max
t mod T < T/2
q
min
otherwise.
(6)
Notice that this reference strategy assumes that the
agent knows in advance the periodicity, T, and the
dynamics of the returns.
4.2.2 Strategy based on Technical Analysis
We include in our study a strategy based on techni-
cal analysis methods, which are frequently used by
traders to forecast returns. For simplicity, we chose
the Moving Least Squares (MLS) technique and con-
sidered an agent with a memory size M to store previ-
ous received returns. This strategy fits a linear trend-
line to the previous M returns, to estimate the next re-
turn, ˆr(t). Noteworthy, once the next return has been
estimated, the agent still needs to perform the cor-
responding adjustment of the investment proportion.
For this, we consider that the agent has a risk-neutral
behavior as follows:
q(t) =
q
min
ˆr(t) ≤ q
min
ˆr(t) q
min
< ˆr(t) < q
max
q
max
ˆr(t) ≥ q
max
(7)
4.3 Results for RoI with Fixed
Periodicity
To elucidate the performance of the adaptive strat-
egy proposed in this paper and the reference strategies
previously presented, we start with a simple scenario
where returns have a fixed periodicity.
First, we assume that the parameters of a strat-
egy lead to an optimal performance, if it leads to
the maximum total budget that can be reached with
this strategy during a complete period of the returns.
When evaluating the strategies, we have to consider
that their performance is also influenced by stochas-
tic effects. In the case of the strategy GACE we also
have to account for the different possible strategies
that may evolve. This means that we have to aver-
age the simulation over a large number of trials, N,
where each trial simulates an agent acting indepen-
dently with the same set of parameter values. For con-
venience, we reinitialize the budget after each cycle of
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
210
the RoI. This is done, because if the strategy performs
well, the budget of the agent may reach very high val-
ues, which would lead to numerical overflows.
4.3.1 GACE Parameter Tuning
The configuration of most meta-heuristic algorithms
requires both complex experimental designs and high
computational efforts. Thus, for finding the best pa-
rameters for the GA, a software called +CARPS (Mul-
tiagent System for Configuring Algorithms in Real
Problem Solving) (Monett, 2004) was used. It con-
sists of autonomous, distributed, cooperative agents
that search for solutions to a configuration problem,
thereby fine-tuning the meta-heuristic’s parameters.
The GA was configured for periodic returns with
T = 100 and different level of noise: σ = 0.1,
and σ = 0.5. Four GA parameters were optimized:
the population size C, the crossover probability p
c
,
the mutation probability p
m
, and the elitism size
s. Their intervals of definition were set as follows:
C ∈ {50, 100,200,500, 1000}, p
c
∈ [0.0, 1.0], p
m
∈
[0.0,1.0], and s ∈ [0.0,0.5]. We show in Table 1 the
best obtained configuration for the GA in the periodic
returns previously mentioned. For clarity, we con-
sidered in these experiments chromosomes with fixed
length, i.e. G
j
= T, and no probability of length mu-
tation, i.e p
l
= 0.
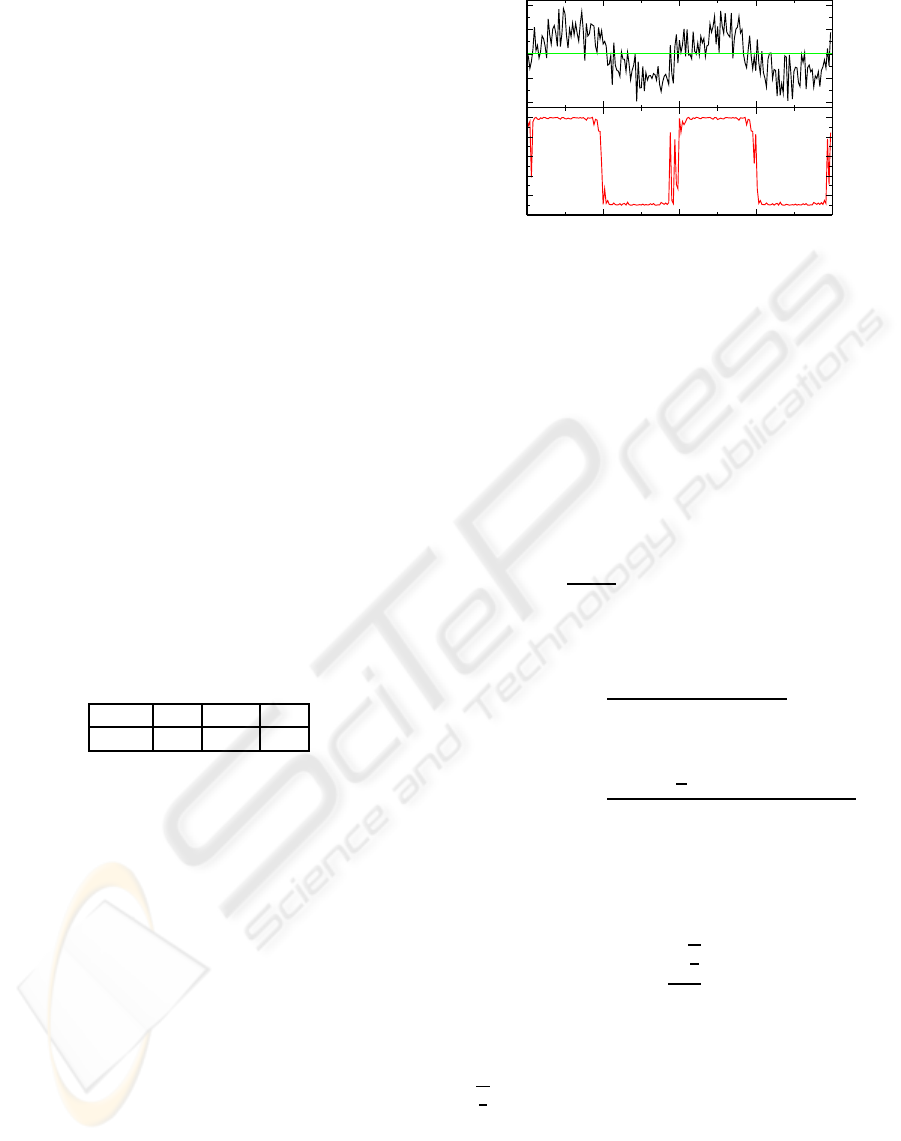
Table 1: GACE’s best pars. for RoI with fixed T.
C p
c
p
m
s
1000 0.7 0.01 0.3
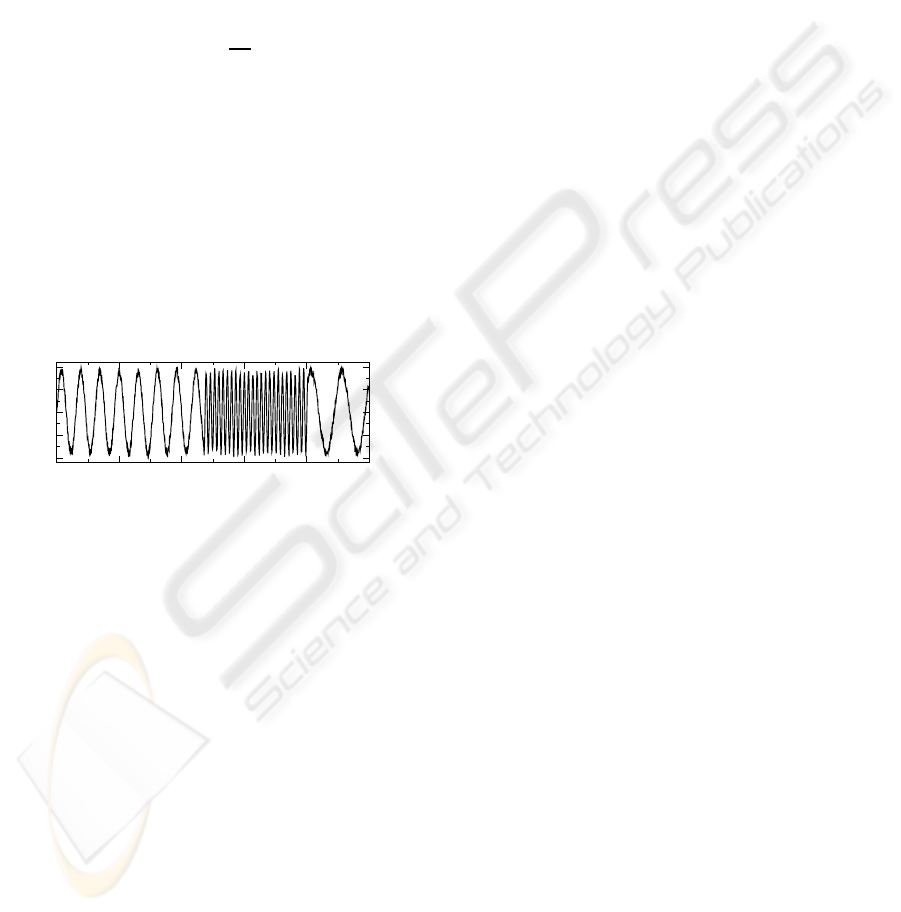
Now, to better illustrate the set of investment
strategies that are being obtained using GACE, we
show in Fig. 2 the RoI and the investment proportions
obtained after a number of time steps. For the reader
with background in signal processing techniques, Fig.
2 may sound familiar as it resembles to those figures
obtained when using matched filters for signal recov-
ery (Turing, 1960).
4.3.2 Performance Comparison
In order to assure fair comparison between the strate-
gies, we need to find the most proper parameter val-
ues for the strategies. Note that for both strategies CP,
Eq. (5) and SW, Eq. (6), we don’t need to tune any
parameters. However, for the strategy MLS, Eq. (7),
we assume that the agent knows the periodicity T of
the returns. This means that the agent needs to de-
termine the most proper memory size, M, based on
the known periodicity of the returns. For this, we per-
formed some computer experiments using MLS with
-1
-0.5
0
0.5
1
r(t)
0
0.2
0.4
0.6
0.8
1
q(t)
99800
99850
99900
99950
100000
t
Figure 2: (Top)Return r(t) and (bottom) investment con-
trol strategy q(t) using GACE after t = 10
5
time steps, for
returns with T = 100 and σ = 0.5.
different memory sizes for returns with different fixed
periodicities, T, and no noise, finding that the most
proper memory size, M, and the periodicity, T, are
proportionally related by M/T ≈ 0.37. Now, if we as-
sume returns with no noise, we can find analytically
the memory size M
⋆
that maximizes the profits. For
this, it can be shown that for periodic returns as in
Eq. (4) with σ = 0, the strategy MLS, Eq. (7), esti-
mates the next return ˆr(t + 1) as follows:
ˆr(t + 1) =
M + 1
M
[sin(ωt) − sin(ωt − ωM)], (8)
where ω = 2π/T. Now, by calculating the average
profits hrqi for the positive cycle of the returns:
hrqi =
T (M+ 1− cos(ωM))
4M
. (9)
And obtaining the derivative of hrqi w.r.t M:
∂
M
hr(t)q(t)i =
−T sin
ω
2
M
2
+ πM sin(ωM)
2M
2
.
(10)
It can be shown that by solving ∂
M
hr(t)q(t)i = 0 and
using Taylor expansion to the sixth order for the sinu-
soidal functions, the memory size M
⋆
that maximizes
the profits corresponds to:
M
⋆
=
q
3
2
π
T. (11)
Consequently, the proportion M/T ≈ 0.37 found
by means of computer simulations approximates
pretty well the proportion found analytically M/T =
q
3
2
/π = 0.389.
Now, we compare the performance of the adap-
tive investment strategy GACE, presented in Sec. 3,
with respect to the reference strategies presented in
Sec. 4.2. For clarity, we assume for the moment that
the strategy GACE uses fixed chromosome length, i.e.
G
j
= G
max
. For all strategies we consider q
min
= 0.1
CONTROLLING INVESTMENT PROPORTION IN CYCLIC CHANGING ENVIRONMENTS
211
and q
max
= 1.0 in our experiments. These parame-
ter values describe the behavior of the strategies CP,
Eq. (5), and SW, Eq. (6). For the strategy MLS,
Eq. (7), we use Eq. (11) to determine the optimal
memory size and for the strategy GACE we use the
parameters in Table 1.
In our experiments we assume that the agent in-
vests in returns with periodicity T = 100 for different
noise levels. We consider here that the length of the
chromosomes is fixed to G
j
= 100 and a new genera-
tion of chromosomes is being obtained after a number
of time steps t
eval
= 100. For the computer experi-
ments, we let the agent to use one of the strategies
to invest during a number of t = 10
5
time steps. In
order to account for the randomness of the scenario,
we perform the experiment for a number of N = 100
trials, gathering the average budget obtained for each
strategy at every 100 time steps.
Fig. 3 shows in a log-log plot the average budget,
hxi, for all strategies in the course of GACE’s gen-
erations, τ. Except for the GACE strategy, all other
strategies have a constant budget in average over each
generation. This occurs because the average of the
budget and the time steps to evaluate the population
of chromosomes were taken at every 100 time steps,
which corresponds to the periodicity of the returns
T = 100. Noteworthy, after 4 and 300 generations
GACE over-performs the strategies CP and MLS and
after 400 generations it performs almost as well as the
strategy SW.
1 10 100 1000
τ
10
0
10
2
10
4
10
6
10
8
10
10
〈
x
〉
SW
MLS
CP, q=0.1
GACE
Figure 3: Average budget, hxi, for different investment
strategies in the course of generations τ, for returns with
periodicity T = 100 and noise σ = 0.1.
4.4 Results for RoI with Changing
Periodicity
In the previous section, we showed results for a sta-
tionary environment, now in this section we tackle a
non-stationary environment.
4.4.1 GA Parameter Tuning
We used again the program +CARPS to find the best
parameters for GACE now for returns with chang-
ing periodicity. The GA was configured for returns
with a maximal periodicity of T
max
= 100 and maxi-
mal elapsing time steps t
max
= 10
4
for different level
of noise: σ = 0.1, and σ = 0.5. In this process, we
used the same intervals of definition as in Sec. 4.3.1,
with the inclusion of the interval: p
l
∈ [0.0,1.0]. The
resulting best parameter values are shown in Table 2.
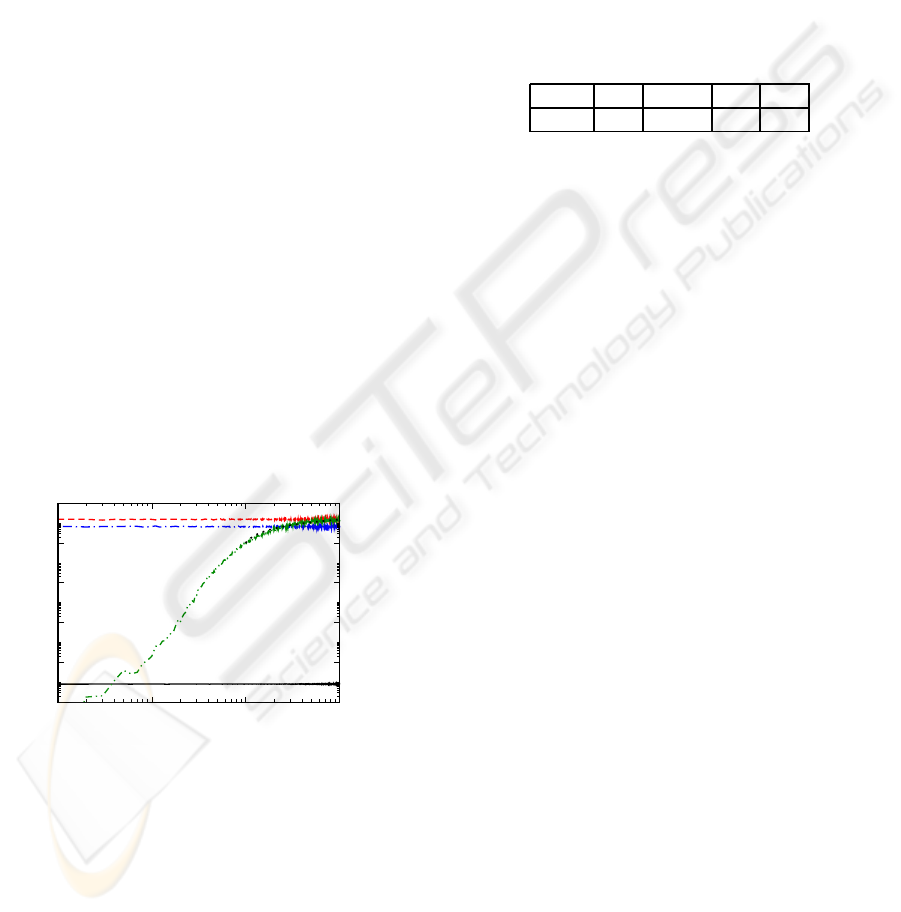
Table 2: GACE’s best pars. for RoI with changing T.
C p
c
p
m
s p
l
1000 0.5 0.001 0.3 0.5
4.4.2 Performance Comparison
In this section we investigate the performance of the
adaptive strategy with respect to the reference strate-
gies in a non-stationary scenario. For this, we per-
formed some computer experiments for returns with
changing periodicity. As we did in the previous sec-
tions, we assumed for all strategies the parameter val-
ues q
min
= 0.1 and q
max
= 1.0 and for the strategy
MLS we used Eq. (11) to calculate the memory size,
M. For the strategy GACE, we used the parameter
values listed in Table 2 and the length of a chromo-
some in the range G
j
∈ (1,G
max
), with G
max
= 200.
We show in Fig. 4 (top) the evolution of budget for
different investment strategies, and (bottom) the cor-
responding periodicity of the returns, Eq.(4), both in
the course of time. Thus, the best strategy is the strat-
egy SW, following the strategy MLS; however, note
that both strategies have total and partial knowledge
about the dynamics of the returns, respectively. This
previous knowledge gives some advantage to these
strategies over the strategy GACE, which only needs
the specification of G
max
. We note that the strategy
GACE evolves quite fast, yielding a set of investment
strategies with a clear tendency to lead more gains
than losses.
5 CONCLUSIONS
In this paper, we presented a simple investment model
and some investment strategies to control the propor-
tion of investment in cyclic changing environments.
The novelty of this paper is in the adaptive investment
strategy here proposed, called Genetic Algorithm for
Changing Environments (GACE), which is a new ap-
proach based on evolution for the correct mapping of
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
212

10
0
10
2
10
4
10
6
10
8
x
CP
SW
MLS
GACE
0 20000 40000 60000 80000 100000
t
0
20
40
60
80
100
T
Figure 4: (Top) Budget for different strategies and (bottom)
Periodicity of the returns, both in the course of time for RoI
with parameters T
max
= 100, t
max
= 10
4
and σ = 0.1.
investment proportionsto patterns that may be present
in the returns. We analyzed the performance of GACE
for different scenarios, and compared its performance
in the course of time against other strategies used here
as a reference. We showed that even though the strat-
egy GACE has no knowledge of the dynamics of the
returns, after a given number of time steps it may
lead to large gains, performing as well as other strate-
gies with some knowledge. This particularly is shown
for long-lasting periodicities, where an ever increas-
ing growth of budget was observed. Further work
includes the analysis of the performance of the strat-
egy GACE for real returns, and to compare the perfor-
mance of GACE against other approaches from Ma-
chine Learning.
ACKNOWLEDGEMENTS
We thank to Dr. Dagmar Monett for providing us the
program +CARPS. We also thank Frank Schweitzer
and H.-D. Burkhard for helpful advice.
REFERENCES
Dawid, H. (1999). Adaptive learning by genetic algorithms:
Analytical results and applications to economic mod-
els. Springer, Berlin.
Geibel, P. and Wysotzki, F. (2005). Risk-sensitive reinforce-
ment learning applied to control under constraints. J.
of Artif. Intell. Res., 24:81–108.
Grefenstette, J. J. (1992). Genetic algorithms for changing
environments. In Manner, R. and Manderick, B., ed-
itors, Parallel Problem Solving from Nature 2., pages
137–144. Elsevier, Amsterdam.
Harvey, I. (1992). The sage cross: The mechanics of recom-
bination for species with variable-length genotypes.
In Parallel Problem Solving from Nature, volume 2,
pages 269–278. Elsevier, Amsterdam.
Holland, J. H. (1975). Adaptation in Natural and Artificial
Systems. The University of Michigan Press.
Kahneman, D. and Tversky, A. (1979). Prospect theory of
decisions under risk. Econometrica, 47:263–291.
Kelly, J. L. (1956). A new interpretation of information rate.
AT&T Tech. J., 35:917–926.
LeBaron, B. (2001). Empirical regularities from interact-
ing long and short horizon investors in an agent-based
stock market. IEEE Transactions on Evolutionary
Computation, 5:442–455.
Magdon-Ismail, M., Nicholson, A., and Abu-Mostafa, Y.
(2001). Learning in the presence of noise. In Haykin,
S. and Kosko, B., editors, Intelligent Signal Process-
ing, pages 120–127. IEEE Press.
Michalewic¸z, Z. (1999). Genetic Algorithms + Data Struc-
tures = Evolution Programs. Springer, Berlin.
Monett, D. (2004). +CARPS: Configuration of Metaheuris-
tics Based on Cooperative Agents. In Blum, C., Roli,
A., and Sampels, M., editors, Proc. of the 1
st
Int.
Workshop on Hybrid Metaheuristics, at the 16
th
Eu-
ropean Conference on Artificial Intelligence, (ECAI
’04), pages 115–125, Valencia, Spain. IOS Press.
Navarro, J. E. and Schweitzer, F. (2003). The investors
game: A model for coalition formation. In Czaja, L.,
editor, Proc. of the Workshop on Concurrency, Speci-
fication & Programming, CS&P ’03, volume 2, pages
369–381, Czarna, Poland. Warsaw University Press.
Navarro-Barrientos, J. E., Cantero-Alvarez, R., Rodrigues,
J. F. M., and Schweitzer, F. (2008). Investments in ran-
dom environments. Physica A, 387(8-9):2035–2046.
Richmond, P. (2001). Power law distributions and dynamic
behaviour of stock markets. The European Physical
Journal B, 20(4):523–526.
Schulenburg, S. and Ross, P. (2001). Strength and money:
An LCS approach to increasing returns. In Lecture
Notes in Computer Science, volume 1996, pages 114–
137. Springer.
Turing, G. (1960). An introduction to matched filters. IEEE
T. Inform. Theory., 6(3):311–329.
Yang, S. (2005). Experimental study on population-based
incremental learning algorithms for dynamics opti-
mization problems. Soft Computing, 9(11):815–834.
CONTROLLING INVESTMENT PROPORTION IN CYCLIC CHANGING ENVIRONMENTS
213
