OPTIMISING

A FLYING ROBOT

Controller Optimisation using a Genetic Algorithm on a Real-World Robot

Benjamin N. Passow

Institute of Creative Technologies, De Montfort University, The Gateway, LE1 9BH Leicester, U.K.

Mario Gongora

Centre for Computational Intelligence, De Montfort University, The Gateway, LE1 9BH Leicester, U.K.

Keywords:

Genetic algorithm, robot, helicopter, PID, control.

Abstract:

This work presents the optimisation of the heading controller of a small ﬂying robot. A genetic algorithm

(GA) has been used to tune the proportional, integral, and derivative (PID) parameters of the helicopter’s

controller. Instead of evaluating each individual’s ﬁtness in an artiﬁcial simulation, the actual ﬂying robot has

been used. The performance of a hand-tuned PID controller is compared to the GA-tuned controller. Tests on

the helicopter conﬁrm that the GA’s solutions result in a better controller performance. Further more, results

suggest that evaluating the GA’s individuals on the real ﬂying robot increases the controller’s robustness.

1 INTRODUCTION

Flying Robots capable of vertical take off and land-

ing (VTOL) including miniature ﬂying robots (MFR),

have gained a strong research interest within the last

decade (Bouabdallah et al., 2007). The manoeuvra-

bility of these robots presents new and exciting possi-

bilities for research, industry, military, and search and

rescue services.

Helicopters are very versatile in their manoeuvra-

bility and have a number of advantages over other

robotic platforms. However, one of the biggest disad-

vantages is the fact that they are nonlinear and highly

unstable systems, very sensitive to external distur-

bances (Bagnell and Schneider, 2001), and are there-

fore difﬁcult to control. A simple manoeuvre like

hovering requires constant control feedback from the

pilot, similar to what a human needs to do when stand-

ing and balancing on a ball. Because of the char-

acteristics mentioned above, a controller for an au-

tonomous helicopter must be fast in computing the

control response. Active control is traditionally im-

plemented using a combination of proportional, inte-

gral, and derivative (PID) control methods (Skogestad

and Postlethwaite, 1996). Such a conventional con-

troller is fast and works well for many control appli-

cations and therefore has been chosen for this work.

Classical PID control techniques have been used be-

fore to stabilise an autonomous helicopter (Puntunan

and Parnichkun, 2002; Sanchez et al., 2005). The dif-

ﬁculty in applying this method is the right choice of

control parameters, and in our case the limited pay-

load of the helicopter for the necessary processing

hardware.

Genetic algorithms (GA) have been used be-

fore for identiﬁcation and optimisation of PID con-

trol parameters (Perhinschi, 1997). A simulator

of the corresponding system is very often used in

order to evaluate the individual’s ﬁtness within a

GA (De Moura Oliveira, 2005). This artiﬁcial model

requires extensive knowledge about the system being

controlled, or the system needs to be identiﬁed to cre-

ate the model. Rather than optimising the controller

using a simulation of the system we have explored

the possibility of using the robot itself for the opti-

misation and evaluation of the controller. By doing

so, the model identiﬁcation becomes implicit and the

system becomes more accurate, more realistic, thus

overcoming the limitation of simulated optimisations

where the quality of the solution is restricted by the

quality of the simulator.

151

N. Passow B. and Gongora M. (2008).

OPTIMISING A FLYING ROBOT - Controller Optimisation using a Genetic Algorithm on a Real-World Robot.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 151-156

DOI: 10.5220/0001496901510156

 SciTePress

2 BACKGROUND

The growth of interest and investigations in UAVs

includes vehicles capable of vertical take off

and landing (VTOL) and miniature ﬂying robots

(MFR) (Bouabdallah et al., 2007). Such vehicles

are very versatile in their manoeuvrability and thus

present an advantageous robotics platform for re-

search in new areas.

Ludington et al. use the GTMax helicopter plat-

form for complex navigational tasks, pattern recog-

nition and test runs involving searching for a certain

pattern on a building and then identifying windows

and doors (Ludington et al., 2006). The achieve-

ment of this work shows what can be done using a

large autonomous helicopter platform. For a small

and light weight indoor helicopter the restrictions de-

mand other approaches.

In general, helicopters have 3 rotational degrees

of freedom (DOF), called pitch, roll and yaw, as well

as 3 translational DOF called up/down, left/right and

forwards/backwards. These outputs are controlled by

four inputs, the amount of lift with the speed and/or

collective pitch of the rotor, the heading with the anti-

torque system or the differential of two rotors, and

the pitch and roll rotational angles which are in turn

controlled by adjusting the rotor blades’ plane angles.

For more information the reader is referred to Coyle,

1996.

The helicopter used in this work is a Twister Bell

47 small indoor helicopter model. It is a coaxial rotor

helicopter with twin counter rotating rotors with ﬁxed

collective pitch and 340 mm. span, driven by two high

performance direct current motors and two servos to

control rotor blades’ plane angles. The weight of the

helicopter in its original state is approximately 210

grams and it can lift up to 120 grams.

A helicopter’s engine causes a torque effect on the

Figure 1: Experimental setup: helicopter strapped to turn

table, ready for the GA tuning.

helicopter. The two engines and rotors of this dual

coaxial rotor helicopter turn in opposite directions,

creating opposite torque effects that cancel each other

out. If one rotor’s speed is reduced whilst the other’s

speed is increased by an identical amount, the heading

will change whilst the amount of lift is maintained.

Helicopter controllers have been successfully im-

plemented using a variety of methods, including clas-

sical PID control (Puntunan and Parnichkun, 2002).

Puntunan and Parnichkun introduce a heading direc-

tion and ﬂoating height PD-controller for a single ro-

tor helicopter. This conﬁrms that classical control

techniques can be used to control helicopter inputs.

The design and evaluation of the controller is of-

ten done on a mathematical model and simulation.

Shim et al. present a study of three control design

methodologies for an autonomous helicopter (Shim

et al., 1998). The controllers are designed and eval-

uated on an artiﬁcial model based on aerodynamics

models.

Sanchez et al. (Sanchez et al., 2005) introduce

an unmanned helicopter control system combining

a Mamdani type fuzzy logic controller (Mamdani,

1974) with PID controllers. The design and evalu-

ation is done using a complex mathematical model.

The system is only tested via simulation for hovering

and slow velocities, but showed good performance.

Perhinschi (Perhinschi, 1997) used GAs to iden-

tify the gain parameters of linear differential equa-

tions which are used to stabilise and control a heli-

copters longitudinal channel. The GAs used a lin-

earised model of a helicopter and the controller per-

formance is not tested in simulation nor on a real he-

licopter.

3 CONTROL ARCHITECTURE

The model helicopter has four actuators to enable the

control of all six DOF. There are two motors which

independently control the speed of each rotor, giving

combined control over altitude and yaw. Two servos

control the lower rotor blades’ plane angles for pitch

and roll control. For autonomy, all of these actuators

need to be controlled by a microprocessor. As only

the heading controller is tuned in this work, only that

part of the system is described in detail.

A digital compass is used to determine the heli-

copter’s heading. The sensor is attached to the tail

of the helicopter to increase the distance to the mo-

tors and thus reduce the interference they have on the

sensor. The sensor is connected to a microchip PIC

microcontroller. The microcontroller handles all on-

board computation, sensor inputs, motor outputs, and

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

152

serial communication used to transfer information to

and from the host computer on which the GA is run-

ning.

The control application running on the microcon-

troller reads all sensors, calculates all four PID control

responses, one for each control input, and then sends

the overall control responses to the actuators. In this

system there are 13 control cycles executed each sec-

ond.

The PID controller is implemented straightfor-

wardly by ﬁrst multiplying the proportional part with

the proportional gain (PGain). Then the integral part

is calculated, multiplying the integral gain (IGain)

with the previous error which is limited by an positive

and negative limit (IMax and IMin). The derivative

part is computed multiplying the change of error with

the derivative gain (DGain). Finally all three results

are added up to get the ﬁnal control response.

There are a number of existing techniques for tun-

ing PID controllers (De Moura Oliveira, 2005). Even

when tuning a PID controller by hand, a variety of

strategies can be applied. The method used in this

work is hand tuning and has been adapted from Smith,

1979. Using this method, the parameters shown in ta-

ble 1 (Value) were identiﬁed.

Table 1: Hand tuned parameters and GA’s parameter range.

Parameter Short Value Range

Proportional gain PGain 0.30 0 - 2.00

Integral gain IGain 0.02 0 - 1.00

Integral state maximum IMax 100 0 - 400

Integral state minimum IMin -100 0 - -400

Derivative gain DGain 0.70 0 - 4.00

4 EXPERIMENTAL SETUP FOR

THE GENETIC ALGORITHM

Genetic algorithms are widely used for search and

optimisation purposes (Holland, 1975; Haupt and

Haupt, 2004). GAs are very useful for optimising

controllers (Fleming and Purshouse, 2002): this ro-

bust and ﬂexible method can handle ill-behaved prob-

lem domains as well as noise and can be used for

multi-objective optimisation.

Rather than using a simulator with the GA, we

optimise the controller on the real ﬂying robot. The

system setup is shown in ﬁgure 1. It shows the dual

rotor helicopter attached to a ball bearing supported

turn table, restricted to turn up to 90

and -90

de-

grees from its middle position at 0

. The fan is used

for cooling down the helicopter’s motors and the em-

bedded system in between tests of individuals. Each

test takes about 20 seconds with an additional 20 sec-

onds to cool the system down. The fan is switched

off while individuals are evaluated. Each individual

is tested by automatically perturbing the helicopter to

each side and analysing the controller’s reaction. This

setup in combination with the GA running on a host

computer, enables the automatic implementation and

evaluation of individuals and thus the execution of the

GA on the real robot without any human intervention.

The GA running on the host computer is conﬁgured

as follows:

Solution Encoding. Based on the hand tuned con-

trollers parameters (table 1), parameter ranges have

been chosen and are shown in table 1. The chromo-

some consists of 5 integer values within that range.

The gain parameters are encoded in steps of one hun-

dredth, and the two integral state limits are encoded

in 16 steps of 25.

Initial Population. The initial population is created

in a random manner, choosing each chromosome ran-

domly within the limits previously deﬁned in table 1.

The population size of 20 is chosen small enough to

have a fast evaluation of each generation while pro-

viding enough individuals to maintain variety.

Evaluation Function. The evaluation function needs

to evaluate each individual on the real helicopter. The

phenotype of an individual is the real helicopter con-

troller where the controller’s parameters are based on

the individual’s chromosome. The evaluation func-

tion is shown in equation 1.

e =

189

∑

t=1

− s)

(1)

where e is the measure of error, t is time, 189 is the

last control cycle of the evaluation, h

is the heading

at time interval t, and s is the setpoint. The ﬁtness

of an individual is inversely proportional to the mea-

sure of error. Squaring the error on each time interval

increases selective pressure on large errors and helps

ﬁnd better solutions more quickly.

The GA program runs on the host computer. To

evaluate an individual, its chromosome is sent to the

helicopter’s embedded system using a direct serial

connection. The helicopter uses the received chromo-

some as the new control parameters, starts the motors

and the controller reacts on the heading error based

on these new parameters. While the controller and

its evaluation are active, the heading sensor data is

sent back to the host computer. In order to test the

controller’s performance on a given error, the heli-

copter is initially and automatically perturbed by 90

to the set point, by driving the two rotors with dif-

ferent power levels. The helicopter turns but cannot

go beyond 90

as the experimental setup physically

OPTIMISING A FLYING ROBOT - Controller Optimisation using a Genetic Algorithm on a Real-World Robot

153

Table 2: Min, mean, max, and standard dev. of measure of

error of 12 tests of hand tuned and best GA individuals.

Min Mean Max StD

Hand tuned 95080 114351 134705 13556

GA tuned 45584 75850 88306 11233

blocks it. At this point the controller starts acting and

is being evaluated. After 92 control cycles the eval-

uation and controller are paused and the helicopter is

perturbed -90

, into the opposite direction. Finally the

controller and its evaluation are started again.

Selection. The selection is based on the ﬁtness com-

bined with random probability, similar to the roulette

wheel strategy, but without the possibility of choos-

ing an individual more than once. With this method

in place, every individual could be chosen for the next

generation although ﬁtter individuals are more likely

to be selected.

Genetic Operators. The individuals selected for the

next generation are copied or changed using crossover

or mutation operators. The best individual is always

copied to the next generation. This process is also

known as elitism. Altogether 20% of the old popu-

lation are copied based on the probabilistic selection.

These individuals are not changed at all.

Crossover is applied by taking the average of an

individual’s chromosome and the chromosome of the

individual next in the probabilistic selection list. 40%

of the next generation are the offspring of the previous

generation’s individuals.

The mutation operator is the source for new va-

riety. It uses a probabilistic approach whereby the

chance of a small mutation taking place is higher than

that of big mutation taking place. This method has

been applied to 40% of the individuals and on each of

its loci.

Termination Criteria. The GA is terminated after

the 30th generation. In order to investigate the GA’s

behaviour no minimum ﬁtness has been deﬁned on

which the GA would terminate.

5 RESULTS AND ANALYSIS

The GA on the real helicopter platform has been run

without the need for manual interaction with the sys-

tem. Three complete runs have been conducted and

the results are shown and discussed now.

With a population size of 20, running for 30 gen-

erations, the GA evaluates 600 individuals from a

search space of over 2 billion. Each individual re-

quires about 20 seconds for evaluation and 20 seconds

Table 3: Solutions of 3 best individuals of 3 independent

GA runs plus measure of error.

PGain IGain IMin IMax DGain Error

0.89 0.98 200 0 2.68 45237

0.83 0.43 75 0 3.13 59385

0.86 0.56 75 0 2.97 59886

0.93 0.34 75 0 3.67 52080

1.08 0.15 0 0 3.95 55174

1.05 0.49 25 0 3.73 56036

0.96 0.69 275 0 3.20 48092

0.93 0.00 0 0 3.15 51827

1.12 0.81 325 0 3.07 53210

0 5 10 15 20 25 30

0.4

0.6

0.8

1.2

1.4

1.6

x 10

Generations

Measure of error

Figure 2: Best individual’s measure of error of each gener-

ation in 3 independent GA runs.

for the helicopter to cool down, thus the overall time

for one GA to ﬁnish is about 6 hours 40 minutes.

Elitism is the method of always copying the best

individual to the next generation. In simulations this

often means a positive or at least zero increase in ﬁt-

ness. Every generation’s best individual’s measure of

error from 3 GA runs is shown in ﬁgure 2. Although

elitism is used in this work, the ﬁtness of the best indi-

viduals of every generation ﬂuctuates and sometimes

even gets worse rather than showing a monotonic in-

crease. The cause for this is the deviation when re-

evaluating an individual. Retesting two individuals

12 times showed a standard deviation of 11233 and

13556 for the measure of error (table 2). This shows a

critical and important difference between using simu-

lated models with an unnatural consistency compared

to working with the real system.

Usually, when there is a suitable solution found

within a simulated system, such as in generation 11

in ﬁgure 2, it is not worth continuing the GA. Using

the real world system, continuing the GA helps en-

sure the consistency of the ﬁnal solutions. Noise and

uncertainties in the system make the GA not converge

to one speciﬁc solution but to a more robust solution.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

154

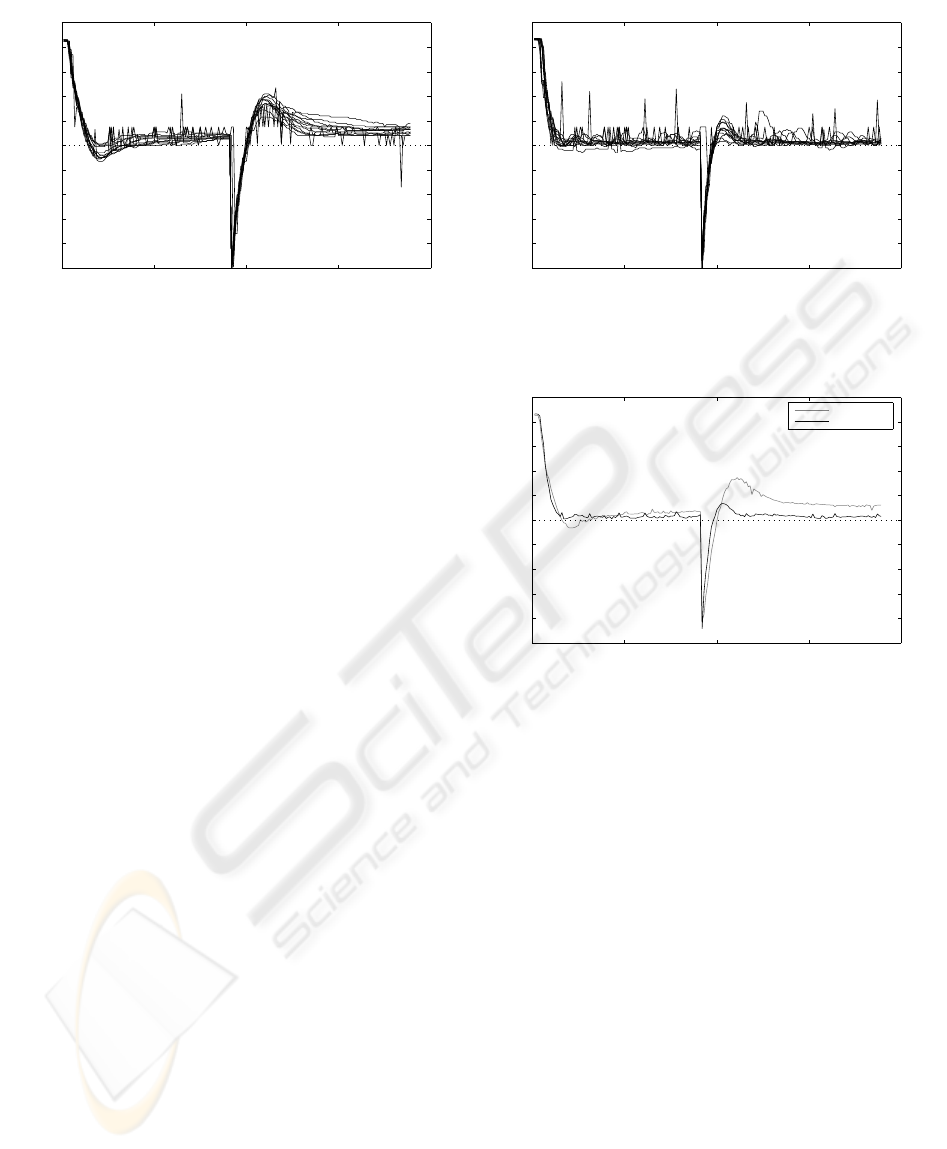
0 50 100 150 200

−100

−80

−60

−40

−20

100

Time [control cycles]

Error [degrees]

Figure 3: Hand tuned PID controller response to heading

perturbed by 90

at t=0 and -90

at t=92. Composite of 12

individual tests.

Table 3 lists the three best solutions of the three in-

dependent GA runs together with their measure of er-

ror. The proportional gain value is similar in all three

GA runs, converging to a good value region. The

small difference between the values indicates that this

parameter has a high impact on the controller’s perfor-

mance. The derivative gain parameter did converge to

a smaller region of values too, but not as restricted as

the proportional gain. On the other hand, the integral

gain together with the integral state minimum value

seem not to be as important for the ﬁtness as they are

not forced into a speciﬁc region of values by the selec-

tive pressure. In contrast, it is quite obvious that the

integral state maximum was forced to be zero. These

results show that the system is not symmetrical. They

show that the helicopter controller needs more gain in

one direction than in the other. This could be caused

by a variance in the motors’ efﬁciency factors, heli-

copter asymmetry, or other causes.

Out of 3 GA runs we chose the one with the least

ﬁt ﬁnal individual. From this GA we used the ﬁttest

individual of the last generation to compare it to the

hand tuned controller. The individual has a PGain

of 0.92, IGain of 0.12, IMin of 250, IMax of 0, and

DGain of 3.64. Figure 3 depicts the response graph

of the hand tuned PID controller perturbed by 90

t = 0 and -90

at t = 92 as a composite of 12 indi-

vidual tests. Figure 4 shows the response graph of the

GA tuned PID controller. Figure 5 presents the plot of

the mean of these 12 tests, for both the GA and hand

tuned controllers.

These graphs conﬁrm that the GA tuned controller

performs better than the hand tuned controller. After

the ﬁrst and positive perturbation, in general the hand

tuned controller does overshoot the setpoint slightly

whereas the GA tuned controller does not. Further-

more, the GA tuned controller reaches the set point

quicker and maintains it more accurately. For the

0 50 100 150 200

−100

−80

−60

−40

−20

100

Time [control cycles]

Error [degrees]

Figure 4: GA tuned PID controller response to heading per-

turbed by 90

at t=0 and -90

at t=92. Composite of 12

individual tests.

0 50 100 150 200

−100

−80

−60

−40

−20

100

Time [control cycles]

Error [degrees]

Hand tuned

GA tuned

Figure 5: GA (black) and hand tuned (gray) PID controllers

response to heading perturbed by 90

at t=0 and -90

t=92. Mean of 12 individual tests for each controller.

second and negative perturbation, in general the GA

tuned controller has less overshoot, approaches the set

point quicker, and maintains it more accurately.

The measure of error from all 12 tests with

the hand tuned and GA tuned controllers has been

recorded and the results are presented in table 2. Over

all 12 tests, based on the measure of error, the hand

tuned controller performed in average 50% worse

than the GA tuned controller.

It is quite normal in a real world system that run-

ning the same experiment again, evaluating the same

individual again, results in a slightly different out-

come. The standard deviation for the 12 hand tuned

and the 12 GA tuned controller evaluations is 13556

and 11233 respectively (table 2). This variation of

results is caused by noise everywhere within the sys-

tem. Due to the natural uncertainties of real systems,

the GA cannot converge to an absolute optimal solu-

tion; rather we have observed that it converges to a

robust approximate optimum that can cope with un-

certainties and noise.

OPTIMISING A FLYING ROBOT - Controller Optimisation using a Genetic Algorithm on a Real-World Robot

155

6 CONCLUSIONS

In this work we introduced a controller optimisation

methodology based on genetic algorithms running on

a real ﬂying robot. A GA has been used to tune the

parameters of a PID controller using the real robot

rather than a simulator to evaluate the individuals.

When the evaluation of GA individuals is done in

a simulator, the performance of the ﬁnal solution that

the GA can ﬁnd, can only be as good as the accu-

racy of the model used for the simulation permits. We

proposed and presented a GA which evaluated the in-

dividuals on a real robot, which made implicit the for-

mal model identiﬁcation.

Furthermore, we presented the results of three GA

runs indicating that its behaviour differs to the be-

haviour often seen on simulated systems. No mono-

tonic increase in ﬁtness is exhibited by the algo-

rithm, although elitism was used. Additionally, re-

evaluating the same GA tuned individual 12 times

manifested a deviation, owing to the real system not

being as artiﬁcially consistent as a simulator, and thus

the GA converging to a more robust controller rather

than to a particular optimal solution.

In order to conﬁrm the GA’s ability to optimise

a controller on the complex real ﬂying robot, the best

control parameters the GA found have been compared

with previously hand tuned control parameters. The

performance of 12 individual tests with each con-

troller was compared, and conﬁrmed that the real ex-

ecution GA found better and more robust solutions.

7 FUTURE WORK

In future work we will use the information from the

GA to identify the robot’s characteristics, which may

be useful to create a very accurate model of it. Based

on the individuals’ parameters and using the sensor

data from the robot we aim to identify the system for-

mally.

With the formal model it may be possible to im-

plement a simulator for the helicopter. At that point a

comparison of two GAs can be conducted, one using

a simulation and the other using the real robot for the

evaluation of individuals.

ACKNOWLEDGEMENTS

We would like to thank Prof. Andrew Hugill, Director

of the Institute of Creative Technologies, De Montfort

University, for his support of this research project.

REFERENCES

Bagnell, J. and Schneider, J. (2001). Autonomous he-

licopter control using reinforcement learning policy

search methods. volume 2.

Bouabdallah, S., Becker, M., and Siegwart, R. (2007).

Autonomous miniature ﬂying robots: coming soon!-

research, development, and results. Robotics & Au-

tomation Magazine, IEEE, 14(3):88–98.

Coyle, S. (1996). The art and science of ﬂying helicopters.

Arnold, Hodder Headline Group.

De Moura Oliveira, P. (2005). Modern heuristics review for

pid control systems optimization: A teaching experi-

ment. In Proceedings of the 5th International Confer-

ence on Control and Automation, pages 828–833.

Fleming, P. and Purshouse, R. (2002). Evolutionary algo-

rithms in control systems engineering: a survey. Con-

trol Engineering Practice, 10(11):1223–1241.

Haupt, R. and Haupt, S. (2004). Practical Genetic Algo-

rithms. Wiley-Interscience.

Holland, J. H. (1975). Adaptation in Natural and Artiﬁcial

Systems: An Introductory Analysis with Applications

to Biology, Control and Artiﬁcial Intelligence. Uni-

versity of Michigan Press.

Ludington, B., Johnson, E., and Vachtsevanos, G. (2006).

Augmenting uav autonomy. Robotics & Automation

Magazine, IEEE, 13(3):63–71.

Mamdani, E. H. (1974). Application of fuzzy algorithms for

simple dynamic plant. IEE Proceedings on Control

Theory and Applications, 121:1585 – 1588.

Perhinschi, M. (1997). A modiﬁed genetic algorithm for

the design of autonomous helicopter control system.

In Proceedings of the AIAA Guidance, Navigation and

Control Conference, pages 1111–1120.

Puntunan, S. and Parnichkun, M. (2002). Control of head-

ing direction and ﬂoating height of a ﬂying robot.

In Industrial Technology, 2002. IEEE ICIT’02. 2002

IEEE International Conference on, volume 2, pages

690–693, Bangkok, Thailand.

Sanchez, E., Becerra, H., and Velez, C. (2005). Combin-

ing fuzzy and pid control for an unmanned helicopter.

In Annual Meeting of the North American Fuzzy In-

formation Processing Society, pages 235–240, Unidad

Guadalajara, Mexico.

Shim, H., Koo, T., Hoffmann, F., and Sastry, S. (1998).

A comprehensive study of control design for an au-

tonomous helicopter. In Decision and Control, 1998.

Proceedings of the 37th IEEE Conference on, vol-

ume 4, pages 3653–3658, Tampa, Florida, USA.

Skogestad, S. and Postlethwaite, I. (1996). Multivariable

Feedback Control: Analysis and Design. Wiley.

Smith, C. (1979). Fundamentals of Control Theory, vol-

ume 86. Chemical Engineering.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

156