OBDD COMPRESSION OF NUMERICAL CONTROLLERS

Giuseppe Della Penna, Nadia Lauri, Daniele Magazzeni

Computer Science Department,University of L’Aquila, L’Aquila, Italy

Benedetto Intrigila

Department of Mathematics, University of Roma ”Tor Vergata”, Roma, Italy

Keywords:

Numerical Controllers, Compression Techniques, Ordered Binary Decision Diagrams.

Abstract:

In the last years, the use of control systems has become very common, especially in the embedded systems

contained in a growing number of everyday products. Therefore, the problem of the automatic synthesis of

control systems is extremely important. However, most of the current techniques for the automatic generation

of controllers, such as cell-to-cell mapping, dynamic programming, set oriented approach or model checking,

typically generate numerical controllers that cannot be embedded in limited hardware devices due to their

size.

A possible solution to this problem is to compress the controller. However, most of the common lossless

compression algorithms, such as LZ77, would decrease the controller performances due to their decompression

overhead.

In this paper we propose a new, completely automatic OBDD-based compression technique that is capable of

reducing the size of any numerical controller up to a space savings of 90% without any noticeable decrease in

the controller performances.

1 INTRODUCTION

Control systems (or, shortly, controllers) are small

hardware/software components that control the be-

havior of larger systems, the plants. A controller con-

tinuously looks at the plant state variables and possi-

bly adjusts some of its control variables to keep the

system in the setpoint, which usually represents its

correct behavior.

In the last years, the use of controllers has become

very common in robotics, critical systems and, in gen-

eral, in the embedded systems contained in a growing

number of everyday products. Therefore, the prob-

lem of the automatic synthesis of control systems is

extremely important.

To this aim, several techniques have been devel-

oped, based on a more or less systematic exploration

of the plant state space. One can mention, among oth-

ers, cell-to-cell mapping techniques (Leu and Kim,

1998), dynamic programming (Kreisselmeier and

Birkholzer, 1994) and set oriented approach (Gr¨une

and Junge, 2005). Recently, model checking tech-

niques have also been applied (Della Penna et al.,

2006; Della Penna et al., 2007b) in the ﬁeld of au-

tomatic controller generation.

The controllers generated using all these tech-

niques are typically numerical controllers, i.e. tables

indexed by the plant states, whose entries are com-

mands for the plant. These commands are used to

set the control variables in order to reach the setpoint

from the correspondingstates. Namely, when the con-

troller reads a state from the plant, it looks up the ac-

tion described in the associated table entry and sends

it to the plant.

However, a main problem of this kind of con-

trollers is the size of the table, which for complex sys-

tems may contain millions of entries, since it should

be embedded in the control system hardware that is

usually very limited.

A possible solution to these problems is to derive,

from the huge numerical information contained in the

table, a small fuzzy control system. This solution is

natural since fuzzy rules are very ﬂexible and can

be adapted to cope with any kind of system. More-

Della Penna G., Lauri N., Magazzeni D. and Intrigila B. (2008).

OBDD COMPRESSION OF NUMERICAL CONTROLLERS.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 43-50

DOI: 10.5220/0001497900430050

 SciTePress

over, there are a number of well-established tech-

niques to guide the choice of fuzzy rules by statisti-

cal considerations, such as in Kosko space clustering

method (Kosko, 1992), by abstracting them from a

neural network (Sekine et al., 1995), by clustering the

trajectories obtained from the cell mapping dynam-

ics (Leu and Kim, 1998) and ﬁnally by using genetic

algorithms (Della Penna et al., 2007a).

However, two considerations are to be made with

respect to this approach. First, the detection of the

fuzzy rules requires (at least) a tuning phase which

is not completely automatic but involves some human

intervention. Second, the fuzzy rules appear not to

be suitable when a very high degree of precision is

needed. This is the case, e.g., of the truck and trailer

parking problem when obstacles are to be avoided in

the parking lot (Della Penna et al., 2006). In this case,

when the truck is near to an obstacle, only a very pre-

cise manoeuvre can park it, without hitting the obsta-

cle. So, to achieve the required precision, an exceed-

ing number of fuzzy rules would be necessary.

Therefore, it seems reasonable to pursue another

possible approach, that is to directly compress the

control table. By this we mean data compression

in the usual sense of reduction of the number of bits

needed to represent the controller table in the com-

puter RAM memory (Cover and Thomas, 2006; Nel-

son and Gailly, 1995).

Observe, however, that in this case the compres-

sion algorithm should be constrained as follows:

1. the logical content of the table, that is the rela-

tion between the states and the correspondingcon-

trol actions, must be preserved without any loss of

information (i.e., we need some kind of lossless

compression algorithm);

2. the access time to the table must be comparable

with the one obtained with a direct representation

of the table in the computer memory (i.e., the de-

compression overhead must be minimal).

Consider as an example the straightforward idea

of directly compressing the table by mean of (some

variant of) the well known Lempel-Zivalgorithm (Ziv

and Lempel, 1977). Since this is a lossless compres-

sion, the ﬁrst requirement above is fulﬁlled, but not

the second one, since the access time to the table

would be linear in the uncompressed size of the table

itself (Nelson and Gailly, 1995).

Since all the common compression algorithms

have similar problemswhen applied to controllers, we

decided to develop a new ad-hoc compression algo-

rithm based on the well known Ordered Binary Deci-

sion Diagrams (OBDDs) (Bryant, 1986).

Decision diagrams as well as decision trees are of

wide use in data manipulation as well as in data min-

ing (Hand et al., 2001). Indeed, our choice of OB-

DDs was motivated by their capability of compress-

ing large state spaces, that is at the hearth of symbolic

model checking and of its great achievements (Burch

et al., 1992; Clarke et al., 1999). Our hypothesis has

been that this capability is transferrable to the com-

pression of the controller table which is, in a sense,

an augmented state space representation.

Our experimental results show that this is indeed

the case. For very large tables we obtain a quite good

compression ratio (around 10:1). Moreover, not only

the access time is good, but it is often even better than

the one obtained by a direct representation of the ta-

ble in memory. This phenomenon is due to the fact

that, unless we accept a very sparse table, with huge

waste of space, we need to represent the controller

using some kind of open addressing table accessed

through a hash function, with a consequent worsen-

ing of the access time (Cormen et al., 2001).

A ﬁnal but very important point to be stressed is

that the implemented compression algorithm, which

transforms the controller table in an OBDD, operates

in a completely automatic way. The only parameter

the user should set is the BDD variable reordering

method (see Section 4), which can effect the com-

pression ratio. After that, the compression operates in

a “zip”-like fashion. However, the best setting of the

above parameter can also be discovered by the algo-

rithm by trying all the possible reorderings, thus mak-

ing the compression process completely automatic.

Finally, a further automatic step can also be applied

to transform the OBDD into C-code that can be in-

corporated in any C-program.

The paper is organized as follows: in Section 2

we give a description of OBDDs and in Section 3

we show how we use them to encode numerical con-

trollers. In Section 4 we present our experimental re-

sults and Section 5 concludes the paper.

2 ORDERED BINARY DECISION

DIAGRAMS

A Binary Decision Diagram (BDD) is a data structure

used to represent a boolean function (Bryant, 1986).

Indeed, any boolean function f can be represented

as a binary tree having two kind of leaf values: F

(boolean false) or T (boolean true). Each node of

the tree (decision node) is labeled by a variable of the

formula f. The two edges outgoing a decision node

represent an assignment of the corresponding variable

to false or true, respectively. Therefore, a path from

the BDD root to one of its leaves represents a (pos-

sibly partial) variable assignment for f , and the cor-

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

responding leaf value is the value of f for the given

assignment.

An advantage of BDDs is that many logical op-

erations, like conjunction, disjunction, negation or

abstraction can be implemented by polynomial-time

graph manipulation algorithms. Indeed, BDDs are ex-

tensively used in the software tools, e.g., to synthesize

circuits or to perform formal veriﬁcations.

If variables appear in the same order on all paths

(or, in other words, if all the nodes on the same tree

level refer to the same variable) the BDD is called

ordered (OBDD).

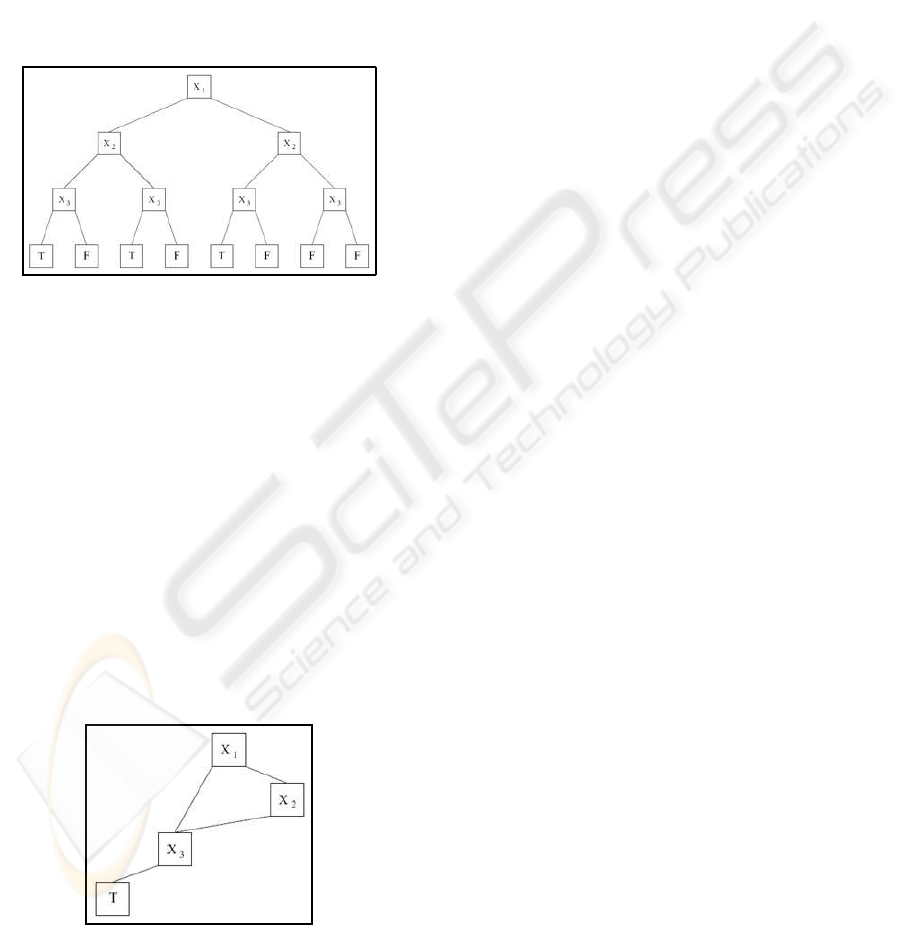
Figure 1: Representation of the boolean function

f(x

, x

) = ¯x

· ¯x

+ ¯x

· x

· ¯x

+ x

· ¯x

As an example, Figure 1 shows the OBDD for the

boolean function f(x

, x

) = ¯x

· ¯x

+ ¯x

· x

¯x

+ x

· ¯x

Usually, OBDDs are also reduced (ROBBD) by

merging isomorphic subgraphs and eliminating nodes

having two isomorphic children. In this way, any

boolean formula f can be represented by an unique

and very compact rooted, acyclic and directed graph.

The size of a reduced BDD is determined both by

the function being represented and by the chosen or-

dering of the variables. Thus, a correct variable order-

ing is of crucial importance to gain the best “reduction

factor”. The problem of ﬁnding the best variable or-

dering is NP-hard, but there exist efﬁcient heuristics

to tackle the problem.

Figure 2: The OBDD in Figure 1 after removal of duplicate

nodes and redundant tests.

Figure 2 shows the reduced version of the OBDD

in Figure 1. Note that all the paths leading to F have

been actually removed from the graph, since they are

simply the complement of those leading to T.

A useful way to see BDDs, that will be used in

this paper, is that they encode the compressed repre-

sentation of a relation. However, unlike other com-

pression techniques, the actual operations on BDDs

are performed directly on that compressed represen-

tation, i.e. without decompression. Details on this

issue are given in Section 3.

3 BOOLEAN ENCODING OF

NUMERICAL CONTROLLERS

OBDDs can be used to create some kind of com-

pressed representation of any data that can be en-

coded as a logical expression. In this Section, we

describe how a numerical controller can be seen as

a boolean formula, and give details on the actual

OBDD-based compression algorithm that has been

implemented. Moreover, we give some informa-

tion on how the OBDD-compressed controller can

be efﬁciently queried and transformed in a hardware-

embeddable form.

3.1 Boolean Encoding of the Controller

Table

As already said, an OBDD can be actually seen

as a compact representation of a relation. On the

other hand, a controller table containing a set of

(state,action) pairs represents a relation R = {(s, a)|a

is the action associated to s in the controller table} be-

tween states and actions. Since BDDs encode formu-

las, it may be useful to represent R through its charac-

teristic function C

deﬁned as follows:

(s, a) =



T if (s, a) ∈ R

F otherwise

Now, to write a deﬁnition of C

as a boolean for-

mula, we ﬁrst have to represent its arguments, i.e.,

states and actions, in terms of logic variables. To this

aim, we expand them to their binary memory repre-

sentation.

Let suppose that states are n-bit values and actions

are m-bit values. We write s[i] and a[i] to denote the

ith bit of state s and action a,respectively.

Let x

, i = 1. . . n and y

, j = 1. . . m be n + m

boolean variables. A state s is then be represented

by the formula

OBDD COMPRESSION OF NUMERICAL CONTROLLERS

, . . . , x

) =

i=1...n

where l



if s[i] = 1

¯x

if s[i] = 0

Each f

is a boolean formula in n variables that is

true if and only if its variables are assigned with the

bits of s (denoting, as usual, the boolean true with 1

and the boolean false with 0). In the same way, an

action a corresponds to the formula

, . . . , y

) =

i=1...m

where l



if a[i] = 1

¯y

if a[i] = 0

Therefore, the controller characteristic function

can be encoded by the boolean formula

, . . . , x

, y

, . . . , y

) =

(s,a)∈R

( f

∧ f

)

is a boolean formula in n+ m variables that is

true if and only if the variable assignment corresponds

to the encoding of a (s,a) pair for which R(s, a) holds.

For example, assume that the controller table con-

tains the following2-bit states s = 00, s

′

= 01, s

′′

= 10,

with the following associated 1-bit actions u = 0, u

′

0, u

′′

= 1. Then the formula for the characteristic rela-

tion would be f

= ¯x

· ¯x

· ¯y

+ ¯x

· x

· ¯y

+ x

· ¯x

· y

3.2 Algorithm for the Logic Encoding of

Numerical Controllers

BDD BDD_encoding(controller_table CTRL) {

read number

of entries in CTRL;

read number

of bits in each state of CTRL;

read number

of bits in each action of CTRL;

foreach j = 1. .. n

create boolean variable

;

foreach j = 1. .. m

create boolean variable

;

BDD

;

foreach i = 1.. . N

{

BDD E,

;

foreach j = 1. .. n //encode state bits

(bit(CTRL[i].state,j) == 1)

∧ x

;

else f

∧ ¯x

;

foreach j = 1. .. m //encode action bits

(bit(CTRL[i].action,j) == 1)

∧ y

;

else f

∧ ¯y

;

E =

∧ f

;

∨

//disjunction of entries

}

return f

;}

Figure 3: Algorithm for the logic encoding of numerical

controllers.

The encoding algorithm, whose pseudocode is

shown in Figure 3, implements the technique de-

scribed in the previous Section.

After reading the number of bits in the controller

states and actions, the

BDD encoding

procedure cre-

ates the corresponding set of boolean variables x

and

, respectively.

Then, for each entry of the controller table, a new

BDD E is created as the appropriate conjunction of

the state and action variables. In particular, the code

checks every bit in the state and adds to the BDD f

a conjunction with the corresponding variable, in its

positive or negated form, based on the value of the bit.

The process is then repeated for the action bits in the

BDD f

, and ﬁnally E is obtained as f

∧ f

The BDD E is then added to the ﬁnal BDD f

using a disjunction. When all the controller entries

have been processed,

BDD encoding

returns f

As we can see, the algorithm is actually very sim-

ple, since all the BDD manipulation is done by the

external BDD package. In particular, our implemen-

tation uses the CUDD (CUDD Web Page, 2007) BDD

manipulation package. Such package provides a large

set of operations on BDDs and many variable dy-

namic reordering methods, which are crucial to gain

the highest possible compression factor (Section 2).

Note that, to ensure the correctness of our ap-

proach, we also developed a parallel-query algorithm

that tests for correctness and completeness the BDD-

encoded controller f

with respect to the original

numerical controller CTRL. This procedure simply

compares the results obtained by querying the un-

compressed and the compressed controller with all the

states in the controller table.

3.3 Querying the Encoded Controller

Once we have compressed the controller table in a

BDD f

, we must show how this information can be

accessed by the controller itself to perform its task.

There are several ways to do this.

A ﬁrst method relies on the fact that the generated

BDD actually encodes a function from states to ac-

tions. In other words, given a state, there is only one

action associated to such state in the controller table.

At the BDD level, this means that if we restrict the

BDD by assigning to the variables x

. . . x

the bits of

a particular state s, then the resulting BDD has only

one satisfying assignment, i.e., the one assigning to

. . . y

the bits of the corresponding action a.

Thus the action associated to a state can be found

by applying two operations (restriction and then de-

duction of satisfying assignments) on the BDD of f

However, since controllers must work in the quickest

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

and simplest possible way, we may consider an alter-

native query method that requires less runtime over-

head.

From the BDD of f

, we extract m different BDDs

. . . f

, one for each bit of the action, in the follow-

ing way.

, . .. , x

) =

∃(y

. . .y

i−1

, y

i+1

, . .. y

)

, . .. , x

, y

. . .y

i−1

, 1, y

i+1

, . .. y

)

In particular, in each f

we existentially abstract

all the action bit variables y

, j = 1. . . m except for

, which is assigned to the constant 1. The resulting

formula f

has n free variables x

. . . x

, which corre-

spond to the state bits.

If we assign x

. . . x

to the binary representation

of a state s, then f

is true if and only if there ex-

ists an action associated to s whose ith bit is 1. Since

the action associated to s, if it exists, is unique, f

actually returns the ith bit of the action associated to

s (assuming, as usual, that the logical true and false

correspond to the values 1 and 0, respectively).

Having these functions at hand, we can rebuild the

binary representation of the action a associated to the

state s by simply applying each f

to the encoding

of s, without any further runtime BDD manipulation.

The execution overhead is minimal in this case, since

the “computation” of the BDD value for a particular

variable assignment requires only a visit of the asso-

ciated graph.

3.4 BDD into C Code Translation

Embedding and querying the BDD-compressed nu-

merical controller within a small hardware or soft-

ware device is also an issue that can be addressed in

various ways.

Obviously, we cannot require CUDD or another

BDD-manipulation package to be present in the con-

troller. However, a BDD (or the set of BDDs obtained

using the technique described in Section 3.3) can be

simply translated in a C code fragment composed by

nested if-then-else statements.

The translation process is very straightforward

and requires only a visit of the OBDD graph. Let n

be a node of the OBDD associated with the logic vari-

able V(n), and let T(n) and E(n) be the two children

of n for V(n) = true and V(n) = false, respectively.

Then, we can deﬁne the C-translation of n as follows:

CT(n) =

(V(n))

THEN

CT(T(n))

ELSE

CT(E(n))

This translation is linear in terms of the required

space, and the resulting representation can be easily

embedded in a (small) hardware device resulting in

good time performances.

4 EXPERIMENTAL RESULTS

To setup our experiments, we ﬁrst have to ﬁx some

BDD encoding parameters, namely the variable or-

dering in the boolean formulas and the dynamic re-

ordering method used by the BDD package.

Indeed, the BDD structure and therefore the com-

pression ratio can be inﬂuenced by the original or-

dering of the variables in the boolean formulas pre-

sented to the BDD package. In particular, we recall

that the variables in our BDDs are the state bit vari-

ables, namely x

, i = 1. . . n, and the action bit vari-

ables, y

, i = 1. . . m. Thus, we may consider the vari-

able orderings arising from all the possible combina-

tions of the following conditions:

• the state bit variables and the action bit variables

can be ordered with different endianness, that is

from the most signiﬁcant bit to the least or vice-

versa;

• the state bit variables can be placed before the ac-

tion bit variables, after them or interleaved.

Namely, we can write the function f

of Section

3 with any of the ten variable orderings O1. . . O10

shown in Table 1. Note that in O9 and O10 we assume

n > m.

Table 1: Possible initial variable orderings.

O1 x

···x

···y

O2 x

···x

···y

O3 x

···x

···y

O4 x

···x

···y

O5 y

···y

···x

O6 y

···y

···x

O7 y

···y

···x

O8 y

···y

···x

O9 x

···x

m+1

···x

O10 x

, y

n−1

m−1

···x

m−n

m−n−1

···x

Moreover, variables can be dynamically reordered

by the BDD package during the construction of the

ﬁnal BDD. In our experiments, we used the fourteen

dynamic reordering methods R1. . . R14 offered by the

CUDD package and shown in Table 2.

In the following experiments we tried all the pos-

sible combinations between initial variable orderings

and dynamic reordering methods, choosing each time

the one that produces the better compression ratio.

All the experiments were performed on a 2.66GHz

Pentium 4 with 1GB RAM.

OBDD COMPRESSION OF NUMERICAL CONTROLLERS

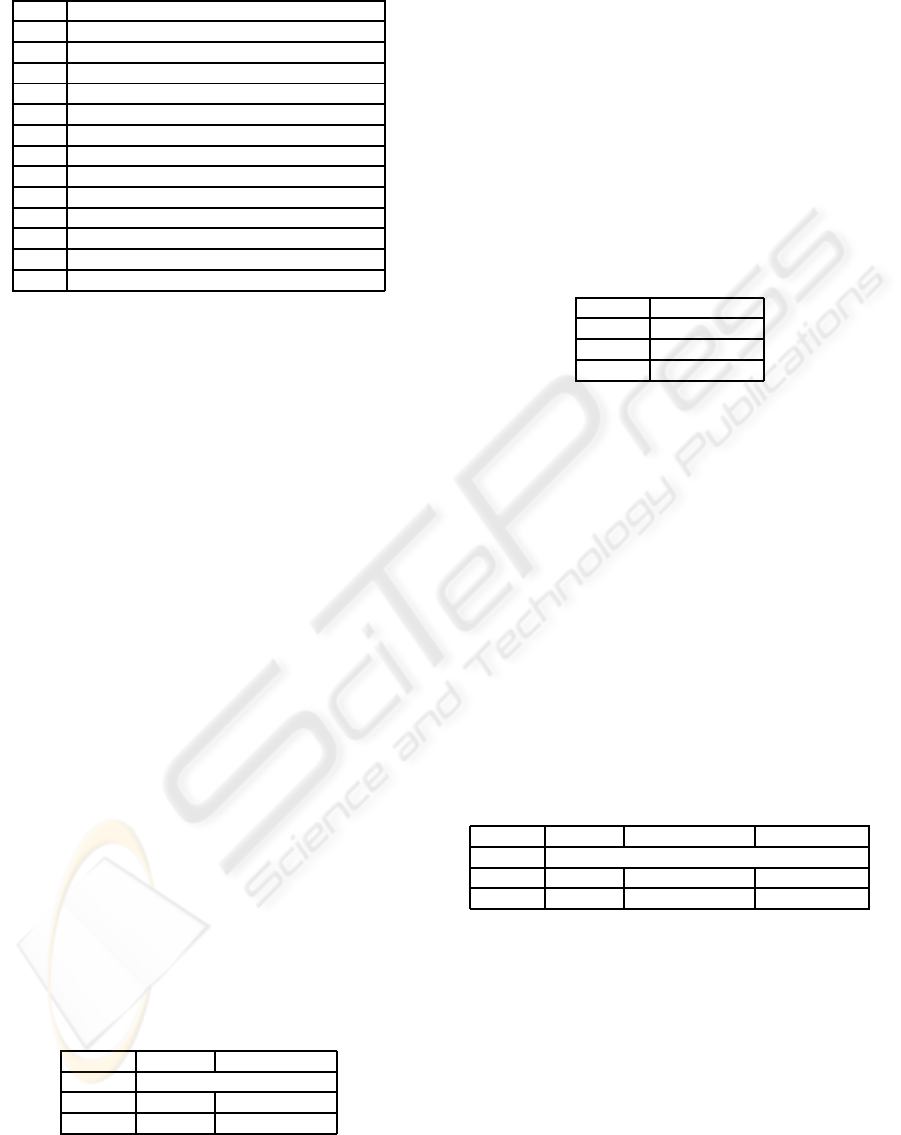
Table 2: CUDD variable reordering methods.

R1 Random reordering

R2 Random pivot reordering

R3 Sift

R4 Converging sifting

R5 Symmetric sifting

R6 Converging symmetric sifting

R7 Group sifting

R8 Converging group sifting

R9 Window permutation (size 2)

R10 Window permutation (size 3)

R11 Window permutation (size 4)

R12 Converging window permutation (size 2)

R13 Converging window permutation (size 3)

R14 Converging window permutation (size 4)

4.1 Inverted Pendulum Controller

The ﬁrst case study is the numerical controller for

the inverted pendulum problem (Kreisselmeier and

Birkholzer, 1994), where the controller has to bring

the pendulum to equilibrium by applying a torque in

the shaft.

The optimal numerical controller was generated

using the dynamic programming method described

in (Kreisselmeier and Birkholzer, 1994). Table 3

shows the details of such controller. In the table, row

Entries indicates the number of controller entries (i.e.,

controlled states) and row Size-column Normal indi-

cates the controller table size in Kilobytes. Moreover,

to compare the effectiveness of the BDD compression

with respect to the common compression techniques,

we also show the size of the controller table com-

pressed by the LZ77-based (Ziv and Lempel, 1977)

algorithm of gzip (GZip Web Page, 2007) (row Size-

column LZ, where the relative size of the compressed

ﬁle is also shown as a percentage) and the average

controller access time in milliseconds for both the un-

compressed and the compressed representations (row

Time-column normal and row Time-column LZ, re-

spectively). Note that, as we expect, access times for

the LZ-compressed controller are very high since, in

the worst case, the controller must be completely de-

compressed to ﬁnd the required table entry.

Table 3: Numerical controller for the inverted pendulum.

Normal LZ

Entries 311618

Size 3043 1295 (42.6%)

Time 8 ms 657 ms

When BDD compression is applied to the con-

troller, we obtain BDDs whose size (in number of

graph nodes) is shown in Table 4 for each combina-

tion of variable initial ordering (O1. . . O10) and dy-

namic reordering (R1. . . R14).

Here, the smallest BDD (indicated by the bold

number in Table 4) has 61584 nodes. The actual

size in Kilobytes and the average access time for the

BDD-compressed controller are shown in Table 5. As

we can see, BDD compression reduces the controller

26.5% more than LZ, and has also better access times

than the LZ-compressed version, since it does not re-

quire any decompression to read the table entries.

Table 5: BDD-compressed numerical controller for the in-

verted pendulum.

BDD

Entries 311618

Size 489 (16.1%)

Time 1 ms

4.2 Truck and Trailer Obstacles

Avoiding Controller

In the second case study, we consider the controller

for the truck and trailer obstacles avoiding problem.

Namely, the controller has to back a truck with a

trailer up to a speciﬁed parking place starting from

any initial position in the parking lot. Moreover, the

parking lot contains some obstacles, which have to

be avoided by the truck while maneuvering to reach

the parking place. Corrective maneuvers are not al-

lowed, that is the truck cannot move forward to back-

track from an erroneous move.

Table 6: Results for the truck and trailer obstacles avoiding

controller.

Normal LZ BDD

Entries 3256855

Size 71650 22644 (31.6%) 7038 (9.8%)

Time 89 ms 3173 ms 108 ms

The numerical controller was generated with the

CGMurϕ tool (CGMurphi Web Page, 2006; Della

Penna et al., 2007b). Results are in Table 6. As we

can see, the controller has a very big size. However,

the best BDD compression scheme (O5,R5) is able to

reduce the size of the controller up to a 90.2% space

savings, that is 21.8% more than using LZ77 com-

pression. Moreover, the BDD compression continues

to win also with respect to the access times.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

Table 4: Number of nodes in the BDD for the inverted pendulum controller with respect to different variable orderings.

O1 O2 O3 O4 O5 O6 O7 O8 O9 O10

R1 92490 108474 65382 64012 156872 83808 149943 86957 92013 145877

R2 142012 145654 66711 78029 130315 79575 144583 89528 148037 142432

R3 65842 61588 65842 61584 138377 75360 145181 143181 65854 127241

R4 65842 71314 70691 61584 130355 71313 75427 135580 65842 65843

R5 65842 65848 70774 70770 144310 70773 144422 70776 65865 142677

R6 65842 65860 70777 70770 135575 70773 135573 70773 65860 130348

R7 66759 66555 92830 61798 144268 61586 136870 61594 69198 65865

R8 65842 61594 75420 61584 145172 61586 135575 61586 65868 65863

R9 92295 92279 65441 61873 163149 121083 255309 121307 101164 178482

R10 76724 77231 61584 61588 134758 122539 143860 78044 79227 142072

R11 72724 72781 61584 61584 134023 122157 134254 106597 77295 134723

R12 81329 98992 61630 61641 134162 128731 138481 79723 86284 136761

R13 77034 65868 61584 61584 134023 123547 134275 111460 66122 134257

R14 65842 65868 61584 61584 134275 77960 134275 116568 68455 134079

4.3 Inverted Pendulum on a Cart

Controller

The last case study is the numerical controller for

the inverted pendulum on a cart problem (Junge and

Osinga, 2004). The system consists of a planar in-

verted pendulum on a cart that moves under an ap-

plied horizontal force, constituting the control. The

position of the pendulum is measured relative to the

position of the cart as the offset angle from the verti-

cal upright position. The controller goal is to set such

angle to zero.

Table 7: Results for the inverted pendulum on a cart con-

troller.

Normal LZ BDD

Entries 151394

Size 1478 90 (6.1%) 215 (14.6%)

Time 3 ms 206 ms 1 ms

The numerical controller was generated with the

CGMurϕ tool. Results are in Table 7. The number

of controller entries is very small with respect to the

previous two case studies. We see that on a small con-

troller the BDD compression has a lower compression

ratio than LZ, but always better access times (1ms vs.

206ms), since it does not require any decompression

to read the table entries.

5 CONCLUSIONS

In this paper, we presented an OBDD based compres-

sion algorithm for numerical controllers. The com-

pression algorithm is completely automatic and can

be applied to the (state,action) tables generated by any

numerical controller generation technique.

Our experiments show that this new algorithm has

a very high compression ratio (up to 10:1), that is of-

ten more than the ratio obtained on the same data by

the most common lossless compression techniques,

such as LZ77. Indeed, OBDD compression is not ac-

tually lossless, but rather “relation-invariant”. That is,

the OBDD compression leaves intact the behavior of

the state-action relation stored in the table. However,

by working on the logic encoding of the relation, the

OBDD is capable of optimizing the representation of

the relation, so reducing its size.

Moreover, accessing the entries of an OBDD-

compressed numerical controller does not require any

data decompression (as it would happen, e.g., with

LZ77), so the controller performances are very good.

Also in this case, the optimized representation gener-

ated by the OBDD sometimes allows to achieve ac-

cess times that are even better that those of an hash

function used on the uncompressed table.

Therefore, the BDD compression is a technique

that can be actually exploited to reduce the size of

numerical controllers, generating a compact structure

that is easy to store and query. This would allow, e.g.,

to use high precision controllers even in limited de-

vices.

Indeed, we are currently studying and implement-

ing algorithms that create embeddable and executable

forms of the OBDD-compressed controllers. The

OBDD-to-C methodology sketched in section 3.4 is

only the ﬁrst step, as we intend to design a transla-

tion process to directly create an optimized VHDL

(Pedroni, 2004) circuit description from the OBDD.

In this way, we would have a completely automatic

methodology to generate, from any numerical con-

troller, a small executable deﬁnition ready to be em-

OBDD COMPRESSION OF NUMERICAL CONTROLLERS

bedded in the hardware.

Finally, a last point we want to investigate is the

relationship between the compression obtained with

the use of the OBDDs and the reduction of fuzzy con-

trol systems by means of a hierarchical approach (see

e.g. (Stufﬂebeam and Prasad, 1999)). Indeed, there is

an evident correspondence between, on one hand, the

search of the best ordering of variables needed for the

OBDD compression and, on the other, the hierarchi-

cal decompositioninto subsystems of a fuzzy system.

REFERENCES

Bryant, R. (1986). Graph-based algorithms for boolean

function manipulation. IEEE Trans. on Computers,

C-35(8):677–691.

Burch, J. R., Clarke, E. M., McMillan, K. L., Dill, D. L.,

and Hwang, L. J. (1992). Symbolic model checking:

states and beyond. Inf. Comput., 98(2):142–170.

CGMurphi Web Page (2006).

http://www.di.univaq.it/magazzeni/cgmurphi.php.

Clarke, E. M., Grumberg, O., and Peled, D. A. (1999).

Model Checking. The MIT Press.

Cormen, T., Leiserson, C., Rivest, R., and Stein, C. (2001).

Introduction to Algorithms. MIT Press.

Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-

mation Theory. Wiley.

CUDD Web Page (2007). http://vlsi.colorado.edu/ fabio/.

Della Penna, G., Fallucchi, F., Intrigila, B., and Magazzeni,

D. (2007a). A genetic approach to the automatic gen-

eration of fuzzy control systems from numerical con-

trollers. In AI*IA, volume 4733 of LNAI, pages 230–

241. Springer-Verlag.

Della Penna, G., Intrigila, B., Magazzeni, D., Melatti,

I., Tofani, A., and Tronci, E. (2006). Au-

tomatic generation of optimal controllers through

model checking techniques. In Proceedings of 3rd

International Conference on Informatics in Con-

trol, Automation and Robotics (ICINCO2006), to

be published in Informatics in Control, Automa-

tion and Robotics III, draft available at the url

http://www.di.univaq.it/magazzeni/cgmurphi.php.

Della Penna, G., Magazzeni, D., Tofani, A., Intrigila, B.,

Melatti, I., and Tronci, E. (2007b). Automatic syn-

thesis of robust numerical controllers. In ICAS ’07,

page 4. IEEE Computer Society.

Gr¨une, L. and Junge, O. (2005). A set oriented approach to

optimal feedback stabilization. Systems Control Lett.,

54(2):169–180.

GZip Web Page (2007). http://www.gzip.org/.

Hand, D. J., Mannila, H., and Smyth, P. (2001). Principles

of Data Mining. MIT Press.

Junge, O. and Osinga, H. (2004). A set oriented approach to

global optimal control. ESAIM Control Optim. Calc.

Var., 10(2):259–270 (electronic), 2004.

Kosko, B. (1992). Neural Networks and Fuzzy Systems.

Prentice Hall.

Kreisselmeier, G. and Birkholzer, T. (1994). Numerical

nonlinear regulator design. IEEE Transactions on Au-

tomatic Control, 39(1):33–46.

Leu, M. C. and Kim, T.-Q. (1998). Cell mapping based

fuzzy control of car parking. In ICRA, pages 2494–

2499.

Nelson, M. and Gailly, J. (1995). The Data Compression

Book. MT Books.

Pedroni, V. (2004). Circuit Design with VHDL. MIT Press.

Sekine, S., Imasaki, N., and Tsunekazu, E. (1995). Appli-

cation of fuzzy neural network control to automatic

train operation and tuning of its control rules. In Proc.

IEEE Int. Conf. on Fuzzy Systems 1993, pages 1741–

1746, Yokohama.

Stufﬂebeam, J. and Prasad, N. (1999). Hierarchical fuzzy

control. In Proceedings of IEEE International Fuzzy

Systems Conference, pages 498–503.

Ziv, J. and Lempel, A. (1977). A universal algorithm for

sequential data compression. IEEE Transactions on

Information Theory, 23(3):337–343.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics