
PATH PLANNING FOR MULTIPLE FEATURES BASED
LOCALIZATION
Francis Celeste, Frederic Dambreville
Dept. EORD FAS Team, DGA, 16 bis av. Prieur de la cte d’Or, 94114 Arcueil, France
Jean-Pierre Le Cadre
IRISA/CNRS, Campus de Beaulieu, 35042 Rennes, France
Keywords:
Path planning, Cram`er Rao Bound, map-based localization, dynamic programming.
Abstract:
In surveillance or exploration mission in a known environment, the localization of the dedicated sensor is of
main importance. In this paper, we discuss the path planning problem for the localization algorithm which
correlates range and bearing measurements and a map composed of several features. The sensor motion
is designed from an information measure derived from the Fisher Information Matrix. It is shown that a
closed form expression of the cost can be obtained. The optimal features location can be neatly geometrically
interpreted. An integral cost which includes the sensor perception limitation is then formulated. It is used in a
dynamic programming framework to tackle the path optimization problem.
1 INTRODUCTION
The path planning problem for map-based localiza-
tion consists in designing the best trajectory for a mo-
bile in a known environment, which guarantees the
highest performance of positioning during its execu-
tion. Data collected from sensors are “matched” to
a prior map to estimate the state (e.g., position and
heading). Depending on the sensor dynamic and the
observation models, different localization algorithms
can be used. When the system is linear or near linear
with Gaussian noises, Kalman-based approaches are
relevant (Thrun et al., 2005; S. Thrun and Dellaert,
2000). In this paper, we introduce a framework to
compute “optimal” path for a moving vehicle which
collects range and bearing data from 2D features. One
of the main challenges is to choose an appropriate
measure to be optimized. In random estimation, the
Fisher Information Matrix (FIM) can be used. We
considered a D-optimal design (Paris and Le Cadre,
2002). The first interesting result of this work is the
derivation of a closed form expression for the FIM
determinant. It is shown that it depends on groups of
two or three features. Then, a geometric analysis of
the optimal features placement can be done. By ex-
ploiting this measure, we introduce an integral cost
functional for a path space, which is composed of el-
ementary moves with constant velocity and constant
heading. Moreover, the sensor field of view limita-
tions are included to the cost computation. At last, we
formulate the problem as finding an optimal path on a
graph by means of dynamic programming. The paper
ends with one illustrative example.
2 PROBLEM FORMULATION
We consider a moving sensor evolving according to
the dynamic model
˙x
t
= v
t
cosϕ
t
,
˙y
t
= v
t
sinϕ
t
,
˙
ϕ
t
= ω
t
. (1)
where its state X
t
∆
= [x
t
,y
t
,ϕ
t
] is composed of its
2-D position and its orientation. A feature map of
its environment is available for localization purpose.
In equation 2, we assume that the known control
u
t
∆
= [v
t
,ω
t
] ∈ U ⊂ R
2
. During its displacement, the
mobile gets sensor measurements from detected fea-
tures which are in the embedded map. Let us denote
f
t
∆
= { f
1
,..., f
m
t
} the set of m
t
features visible and
used in the localization process at time t. Each fea-
ture is defined by its 2D position in a global frame
214
Celeste F., Dambreville F. and Le Cadre J. (2008).
PATH PLANNING FOR MULTIPLE FEATURES BASED LOCALIZATION.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 214-219
DOI: 10.5220/0001498102140219
Copyright
c
SciTePress

R
g
∆
= (O,
−→
u ,
−→
v ):
f
i
↔
x
i
,y
i
∈ D ⊂ R
2
. (2)
and the “sensor-feature” vector δp
i
(t)
∆
=
x
i
− x
t
, y
i
− y
t
∗
. The measurements vector is
the stacked vector Z
t
=
z
t
1
,...,z
t
m
t
where z
t
i
is the
range and bearing measurement for feature f
i
. So,
the observation model stands as follows :
Z
t
= H
t
(X
t
,f
t
) + W
t
. (3)
where the 2×i
th
and 2×i+ 1
th
elements of H
t
(X
t
,f
t
)
are the components of the two dimensional vector
h(X
t
, f
i
) given by
z
t
i
= h(X
t
, f
i
) + w
i
t
. (4)
h(X
t
, f
i
)
∆
=
(
p
(x
t
− x
i
)
2
+ (y
t
− y
i
)
2
atan
2
(
y
i
−y
t
x
i
−x
t
) − ϕ
t
(5)
The noise vector w
i
t
is modelled by an i.i.d. Gaus-
sian process with zero mean and covariance matrix
Σ
i
t
. Moreover, we suppose that Σ
i
t
= Σ,∀i and
Σ =
σ
2
r
0
0 σ
2
ϕ
. (6)
We also consider that w
j
t
and w
l
t
are independent for
l 6= j. So in light of (2), the likelihood function is
given by
p(Z
t
|X
t
) ∝ exp
−
1
2
m
t
∑
l=1
kz
l
− h(X
t
, f
l
)k
2
Σ
!
. (7)
If
ˆ
X
t
is one estimate based on the measurement Z
t
(e.g., the maximum likelihood estimate), the covari-
ance error e
X
t
= X
t
−
ˆ
X
t
is lower bounded by the
Cramer Rao Bound (CRB) (Van Trees, 1968).
Cov(e
X
t
) ≻ F
−1
(t). (8)
The calculation of the FIM F(t) is given in our case
by,
F =
m
t
∑
i=1
∂h(X
t
, f
i
)
∂X
t
∗
Σ
−1
∂h(X
t
, f
i
)
∂X
t
. (9)
The elementary gradient vector can be derived
straightforwardly
∂h(X
t
, f
i
)
∂X
t
=
c
i
s
i
0
−
s
i
ρ
i
c
i
ρ
i
−1
. (10)
where α
i
(t)
∆
= ∠
−→
u δp
i
(t), ρ
i
∆
= ||δp
i
(t)||, c
i
∆
= cosα
i
and s
i
∆
= sinα
i
. Let us also introduce the following
notations :
• ~c
∆
= [c
1
···c
m
t
]
∗
,~s
∆
= [s
1
···s
m
t
]
∗
,
• ~c
ρ
∆
= [
c
1
ρ
1
···
c
m
t
ρ
m
t
]
∗
,~s
ρ
∆
= [
s
1
ρ
1
···
s
m
t
ρ
m
t
]
∗
.
• 1
m
t
∆
= [1···1]
∗
, 0
m
t
∆
= [0···0]
∗
Without loss of generality, we set σ
d
= σ
ϕ
= 1 then
we can rewrite
1
F(t) = G(t)G(t)
∗
. (11)
with
G(t) =
G
1
(t)
z}|{
G
2
(t)
z}|{
~c
t
~s
ρ
t
~s
t
−~c
ρ
t
0
m
t
1
m
t
.
(12)
G(t) is a 3 × 2m
t
matrix with columns G
i
are part of
the subset G
1
(t) or G
2
(t) :
G
1
(t) =
G
i
1
,1 ≤ i
1
≤ m
t
|G
i
1
=
c
i
1
s
i
1
0
∗
,
G
2
(t) =
n
G
i
2
,1 ≤ i
2
≤ m
t
|G
i
2
=
s
i
2
ρ
i
2
−
c
i
2
ρ
i
2
1
∗
o
.
In this paper, we are dealing with the optimization
of the sequence of displacement which provides the
“best” estimate of the state. This can be achieved us-
ing an appropriate measure of information gain. We
adopt here a D-optimal design considering the deter-
minant of the FIM
2
. In the next section, we show
that this measure is a function implying the esti-
mated bearings angles (α
i
(t))
m
t
i=1
and relative ranges
(ρ
i
(t))
m
t
i=1
.
3 DERIVATION OF det(F)
Let us define L (t) as the determinant of the FIM at
time t in position X
t
. From (11), we have
L (t) = det(G(t)G(t)
∗
). (13)
Using the Binet-Cauchy formula
3
, we can notice that
L (t) =
∑
1≤i< j<k≤2m
t
det(G
i
,G
j
,G
k
)
2
. (14)
hence to compute L (t), we have to enumerate the
different cases in accordance with the column vec-
tors (G
i
,G
j
,G
k
) are in G
1
or G
2
. In the following,
we denote d
ijk
∆
= det(G
i
,G
j
,G
k
). If all columns are
in G
1
, d
ijk
is trivially equal to zero. Using determi-
nant computation properties and relations betweeen
trigonometric functions, we get
1
* is the transpose operator
2
other matrix operator can be used, such as the trace
3
det(AB) =
∑
S
det(A
s
)det(B
s
), S = {1,·· · , n}, if A ∈
M
K
(m,n) et B ∈ M
K
(n,m), A
s
is the m× n matrix whose
columns are those of A with in S
PATH PLANNING FOR MULTIPLE FEATURES BASED LOCALIZATION
215
a) G
i
,G
j
∈ G
1
and G
k
∈ G
2
d
1
ijk
= sin(α
i
− α
j
).
b) G
i
∈ G
1
and G
k
, G
j
∈ G
2
d
2
ijk
=
cos(α
i
− α
k
)
ρ
k
−
cos(α
i
− α
j
)
ρ
j
.
c) G
i
∈ G
1
, G
j
and G
k
∈ G
2
d
3
ijk
=
sin(α
i
− α
k
)
ρ
i
ρ
k
+
sin
α
i
− α
j
ρ
i
ρ
j
+
sin
α
j
− α
k
ρ
j
ρ
k
.
In conclusion, we notice that L (t) is the sum of three
terms L
1
(t), L
2
(t)andL
3
(t) which characterize inter-
actions between pairs and triplets of visible features.
L (t) = a
1
L
1
(t) + a
2
L
2
(t) + a
3
L
3
(t). (15)
with L
1
(t) =
∑
m
t
i=1
∑
m
t
j>i
g
1
( f
i
, f
j
), L
2
(t) =
∑
m
t
i=1
∑
m
t
j=1
∑
m
t
k> j
g
2
( f
i
, f
j
, f
k
) and L
3
(t) =
∑
m
t
i=1
∑
m
t
j>i
∑
m
t
k> j
g
3
( f
i
, f
j
, f
k
) where (g
l
)
l∈{1,2,3}
are respectively given by the square of d
l
ijk
in the
above cases. Coefficients (a
l
)
1≤l≤3
depend on σ
r
and
σ
ϕ
.
4 THE OPTIMAL PLACEMENT
OF THE FEATURES
We now study the location of the features which pro-
vides the best performance of estimation around a
given mean state
¯
X. The analysis takes into account
the sensor field of view and only consider L
1
(t) (pairs
interaction). Such an approximation is valid when
σ
d
ρ
≪ σ
ϕ
. Let ( f
i
)
1≤i≤n
be visible from state
¯
X. We
introduce P = (¯x; ¯y), (~v
i
)
1≤i≤n
, D
m
, ~v
−
and ~v
+
(see
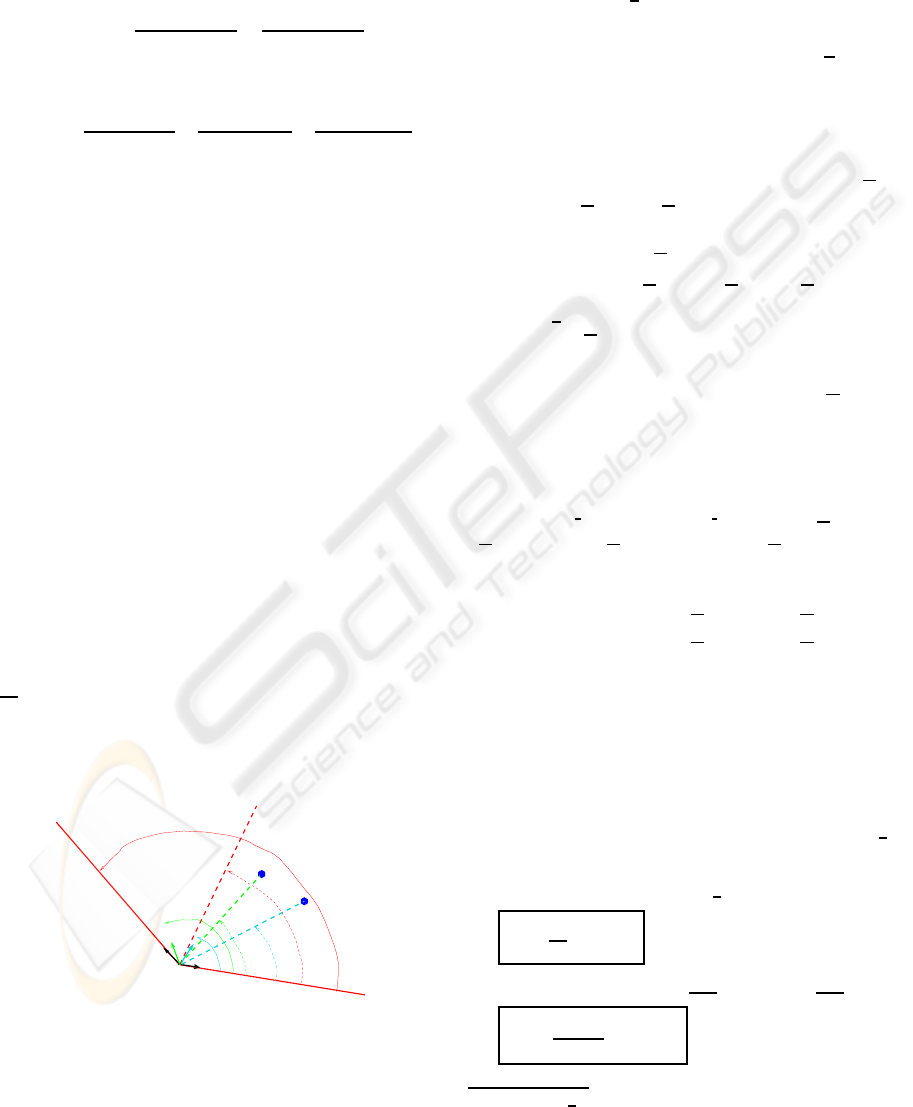
figure 1). D
m
is the angular aperture of the sensor field
of view. An analogy can be made with the reasoning
P
v−
v+
f
1
f
2
α
2
α
1
2α
2
2α
1
~v
1
~v
2
D
m
2D
m
Figure 1: Sensor features spatial configuration.
in (Gu et al., 2006) for multiple UAVs cooperation
for sensing. The derivation made here is nevertheless
simpler and more geometrically intuitive.
Proposition 1
. Maximizing L
1
(t) is equivalent to
find the configuration (~v
1
∗
,...,~v
n
∗
) which minimizes
||~v
T
|| = ||
∑
n
i=1
~v
i
||
2
.
Indeed, using classic trigonometric properties
4
we
can show that L
1
=
1
4
1− ||
∑
n
i=1
~v
i
||
2
.
4.1 Optimal Placement for D
m
<
π
2
In this context, the value of the angle made by vectors
~v
i
and ~v
j
is strictly smaller than π. So ||~v
T
|| > 0. Let
i
0
∈ {1,··· ,n} and θ
i
0
= ∠ ~v
−
~v
i
0
. We also denote ~v
i
0
∆
=
∑
j6=i
0
~v
j
and θ
i
0
= ∠ ~v
−
~v
i
0
||~v
T
||
2
= ||~v
i
0
+ ~v
i
0
||
2
= 1+ ||~v
i
0
||
2
+ 2||~v
i
0
||cos
θ
i
0
− θ
i
0
.
As D
m
<
π
2
, ~v
i
0
is also between ~v
−
and ~v
+
. So, for
a given placement of vectors {~v
i
}
i6=i
0
, ||~v
T
|| is min-
imized for θ
∗
i
0
which makes g(θ
i
0
) = cos
θ
i
0
− θ
i
0
minimum.
Proposition 2. In the optimal configuration, each
vector ~v
i
is on the frontier of the visibility cone.
Proof. 0 ≤ θ
i
,θ
i
0
≤ 2D
m
⇒ θ
i
0
− 2D
m
≤ θ
i
0
− θ
i
0
≤
θ
i
0
. Moreover, θ
i
0
− 2D
m
> −π et θ
i
0
< π. We can
easily deduce that
θ
∗
i
0
=
(
2D
m
if |θ
i
0
− 2D
m
| > θ
i
0
0 if |θ
i
0
− 2D
m
| < θ
i
0
.
which proves that either ~v
i
0
= ~v
−
or ~v
i
0
= ~v
+
. Let us
denote n
−
and n
+
the number of vectors ~v
i
respec-
tively equal to ~v
−
and ~v
+
(n
−
+ n
+
= n). n
−
must
verify the relation
||~v
T
||
2
= 2(1− a)n
2
−
− 2(1− a)nn
−
+ n
2
∆
= f(n
−
).
with a = cos(2D
m
) (a < 1). f is minimal for n
−
=
n
2
,
so
• if n is even, n
−
= n
+
=
n
2
and which provides
L
1
=
n
2
4
sin
2
(D
m
) .
• else we can set n
−
=
n−1
2
and n
+
=
n+1
2
, then
L
1
=
n
2
− 1
4
sin
2
(D
m
) .
4
sin
2
a =
1
2
(1 − cos2a) and cos(a − b) = cosacosb +
sinasinb
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
216

4.2 Optimal Placement for D
m
>
π
2
In this case, we have to make a different reasoning ac-
cording to the parity of n. When n is even, the optimal
solution is obvious as we can place the features so that
~v
T
=
~
0. Indeed, it is enough to choose {~v
1
,··· ,~v
n
}
pairwise such that their difference angle is equal to π
(i.e. orthogonal assignment of features). We can no-
tice that, there are plenty of such configurations and
the cost is L
1
=
n
2
4
. Otherwise, if n is odd, it is more
difficult to find a placement which gives ~v
T
=
~
0. Nev-
ertheless, we can search among a particular class of
configurations with ~v
i
0
= −~v
i
0
. Assuming i
0
= n, one
way to obtain ~v
n
collinear and opposite to ~v
n
, is to
choose {~v
1
,··· , ~v
n−1
} where
∃ϕ ∈
i
π
2
,π
h
,
∠~v
i
~v
n
= ϕ, ∀i ∈ {1, · ·· ,
n−1
2
},
∠~v
n
~v
j
i
= ϕ, ∀ j
i
= i+
n−1
2
.
Given ∠ ~v
−
~v
i
= θ
p
, ∀i ∈ {1, · ·· ,
n−1
2
} and supposing
~v
−
=~u, then
~v
n
= cos(ϕ+ θ
p
)~u+ sin(ϕ+ θ
p
)~v,
~v
i
= cos(θ
p
)~u+ sin(θ
p
)~v, ∀i,
~v
j
i
= cos(2ϕ+ θ
p
)~u+ sin(2ϕ+ θ
p
)~v, ∀ j
i
.
and ∀i ∈ {1,··· ,
n−1
2
}
~v
i
+ ~v
j
i
= cos(θ
p
) + cos(2ϕ+ θ
p
)~u
+sin(θ
p
) + sin(2ϕ+ θ
p
)~v. (16)
Using trigonometric properties, we get that:
~v
i
+ ~v
j
i
= 2cos(ϕ)(cos(ϕ+ θ
p
)~u+ sin(ϕ+ θ
p
)~v)
= 2cos(ϕ)~v
n
.
To make ~v
T
=
~
0 , we must force
~v
n
+
n−1
2
∑
i=1
~v
i
+ ~v
j
i
=
~
0,
which is equivalent to the following condition on ϕ.
l(ϕ)
∆
= 1+ (n− 1)cos(ϕ) = 0, ϕ ∈
h
π
2
,π
h
. (17)
As the field of view is limited, we have to satisfy
ϕ ≤ D
m
. Therefore, if such an angle exists, the cost
value is again L
1
=
n
2
4
. In particular, if D
m
>
2π
3
,
we can always find an optimal placement. Indeed,
it is sufficient to choose n − 3 vectors as in the even
case (orthogonal assignment) and to use the last three
with ϕ =
2π
3
. When exists ϕ solution of (17) with
D
m
< ϕ <
2π
3
, it seems difficult to find a configuration
which allows to attain the maximum cost. But, we
propose a suboptimal solution which minimizes l(ϕ).
l is decreasing on
π
2
,D
m
(
∂l
∂ϕ
∝ −sin(ϕ) < 0) so its
maximum is given for ϕ = D
m
. This leads to the cost
value
L
1
=
1
4
n
2
− (1+ (n− 1)cos(D
m
))
2
.
In this section, we made a geometric analysis to de-
termine the optimal placement of the features to max-
imize the cost L
1
. Making the same kind of reasoning
for the complete cost L (t) is much more challeng-
ing. After this static analysis, we deals with the path
planning problem in the next section. For the sake of
brevity, we only detail the approach for L
1
(t) but it
can be generalized to L
2
(t) and L
3
(t).
5 PATH PLANNING
We consider the evolution of the sensor between
[t
0
,t
f
] with 0 < t
f
≤ T∗ from position q
s
∈ D to po-
sition q
t
∈ D . We look for paths (X
t
)
t∈
[
t
0
,t
f
]
which
maximizes the cost
Ψ([t
0
,t
f
]) =
Z
t
f
t
0
L
1
(t)dt. (18)
The problem can be formalize in the optimal control
framework with two boundaries constraints. Unfortu-
nately, due to the cost expression and the sensor field
of view (FOV) limitations, no analytic formulation of
the optimal path can be derived. An approximated
approach based on the discretization of the state and
control space seems more tractable.
5.1 Path Description
As in (Celeste et al., 2007), We formalize here
the problem as a discrete path planning. A regu-
lar grid is considered and one path is a sequence
of elementary displacements with constant heading
ϕ ∈ { ϕ
i
=
i∗π
4
, i ∈ {−3,...,4}}
and constant veloc-
ity v (a leg). For a path τ with n
τ
legs, the cost is as
follows:
Ψ([t
0
,t
f
]) =
n
τ
−1
∑
i=0
Z
t
i+1
t
i
L
1
(t)dt. (19)
X
t
0
= q
s
and X
t
n
τ
−1
= q
t
are supposed to be on the
grid. Some constraints on the maneuvers can be im-
posed to avoid chaotic behavior (e.g. bang-bang ef-
fect)(Paris and Le Cadre, 2002). To solve the planning
task we need to compute the cost associated with each
leg. First of all, it is necessary to determine the part of
the leg where each feature is visible due to the sensor
FOV.
PATH PLANNING FOR MULTIPLE FEATURES BASED LOCALIZATION
217

5.2 Cost for One Leg
For a FOV model with an aperture 2∆ and a maximum
range detection R
d
, the area Z visible from the leg e is
composed of three regions Z
1
, Z
2
and Z
3
(see Figure
3). A pair of features ( f
i
, f
j
) ∈ Z
2
are visible from
P
ij
−
(x
ij
−
,y
ij
−
) and P
ij
+
(x
ij
+
,y
ij
+
). These limits can be de-
rived using a simple geometric reasoning. Moreover,
S2
S1
S3
S4
Z
1
Z
2
Z
3
S
T
Figure 2: The visible region for one leg.
we have a relation between an elementary displace-
ment and the associated duration (dt ∝ dx if ϕ 6=
π
2
[π],
dt ∝ dy else). and the leg can be reparametrized as
follows:
• y(x) = β+ γx, ∀x ∈ [x
S
,x
T
] if ϕ 6=
π
2
[π] (non verti-
cal motion),
• x = x
S
, y
S
≤ y ≤ y
T
else (vertical motion),
The total cost for a leg e can then be computed using
relevant change of variable.
For non vertical displacement, the cost due to
a pair of features ( f
i
, f
j
) is the integral of a rational
function:
K
ij
(x) =
(x− x
i
)(y(x) − y
j
) − (x− x
j
)(y(x) − y
i
)
2
p
i
(x)p
j
(x)
.
where p
l
(x) = (x− x
l
)
2
+ (y(x)− y
l
)
2
∆
= a
l
x
2
+ b
l
x+
c
l
, l ∈ { j, i} is the respective square range of f
i
, f
j
to the sensor. Therefore, these polynomials are irre-
ducible whatever the sensor position in D \
f
i
, f
j
.
We can rewrite
K
ij
(x) =
(A
ij
x+ B
ij
)
2
p
i
(x)p
j
(x)
. (20)
So, we have to compute:
c
nv
ij
(e) ∝
Z
x
ij
+
x
ij
−
K
ij
(x)dx. (21)
which can be done with a relevant partial expansion
of the rational function. Nevertheless, we have to pay
attention to the position of the leg relativelyto the fea-
tures.
case (1) e is on the perpendicular bisector of [ f
i
f
j
],
then p
j
(x) = p
i
(x),∀x and
(A
ij
x+ B
ij
)
2
p
i
(x)p
j
(x)
=
r
1
x+ s
1
p
i
(x)
+
r
2
x+ s
2
p
2
i
(x)
. (22)
case (2) e is not on the perpendicular bisector of
[ f
i
f
j
], then
(A
ij
x+ B
ij
)
2
p
i
(x)p
j
(x)
=
r
1
x+ s
1
p
i
(x)
+
r
2
x+ s
2
p
j
(x)
. (23)
Identification of the numerators yields in both
cases to a linear system to deduce χ = [r
1
r
2
s
1
s
2
]
∗
,
M
(c)
ij
χ = B
ij
, for cases c = 1, 2 (24)
M
(1)
ij
=
a
i
0 0 0
b
i
0 a
i
0
c
i
1 b
i
0
0 0 c
i
1
, B
ij
=
0
A
2
ij
2A
ij
B
ij
B
2
ij
(25)
and
M
(2)
ij
=
a
i
a
j
0 0
b
i
b
j
a
i
a
j
c
i
c
j
b
i
b
j
0 0 c
i
c
j
(26)
For vertical displacements, it is more appropriate to
consider integration with the variable y. The same
reasoning leads to the integration of a rational func-
tion to get the cost expression
c
v
ij
(e) ∝
Z
y
ij
+
y
ij
−
K
ij
(y)dy. (27)
5.2.1 Closed Form Expression for the Cost
Whatever the leg orientation, we have to deals with
the computation of integrals of the form (n ∈ {1,2},
l ∈ {i, j}):
H
(n)
(l,u, v, x
−
,x+) =
Z
x
+
x
−
ux+ v
(ax
2
+ bx+ c)
n
dx (28)
Using specific changes of variable and classic prim-
itives, the closed form expression for the cost (21),
(27) can be derived. For instance,
H
(1)
(l,u, v, x
−
,x+) = ν
(1)
l
ln
|p
l
(x
+
)|
|p
l
(x
−
)|
+
λ
(1)
l
tan
−1
(q
l
(x
+
+
b
l
2a
l
)) − tan
−1
(q
l
(x
−
+
b
l
2a
l
))
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
218

where q
l
=
r
4a
2
l
4a
l
c
l
−b
2
l
, ν
(1)
l
=
u
2a
l
and
λ
(1)
l
=
2va
l
−ub
l
2a
2
l
q
l
.
The expressions of the costs are finally
c
ij
(e) = H
(1)
(i,r
1
,s
1
,x
ij
−
,x
ij
+
) + H
(n)
( j, r
2
,s
2
,x
ij
−
,x
ij
+
)
where n ∈ {1,2} depends on the leg orientation ac-
cording to [ f
i
, f
j
]. Given the contribution of each vis-
ible pair of features, the complete cost of the leg is
given by c(e) =
∑
i, j
c
ij
(e) Therefore, the cost associ-
ated to a path τ = {e
1
,··· ,e
n
} of length n = n
τ
− 1
is c(τ) =
∑
n
i=1
c(e
i
). The optimization can then be
solved via dynamic programming.
6 EXPERIMENT
In this experiment, we consider an embedded map
composed of ten features organised on the border of
D = [0;200;0;200]. The sensor FOV is character-
ized by a maximum range detection R
max
= 70m and a
half aperture angle D
m
= 120 deg.. Moreover, the au-
thorized difference angle between two following time
steps must be bounded by π/4 and the path length
smaller than l
max
= 98 legs from q
s
= (20;20) to
q
t
= (170;20). The grid resolutions are δx= δy = 10.
The algorithm seems to behave well. The sensor
0 20 40 60 80 100 120 140 160 180 200
0
20
40
60
80
100
120
140
160
180
200
path planning
q
s
q
f
Figure 3: Optimal path, features(green), q
s
and q
f
(blue).
moves in order to be as soon as possible on the per-
pendicular bisector of pairs of features and to increase
the number of visible pairs. The proposed path allows
to provide better triangulation conditions which im-
proves the estimation process. Moreover some inter-
esting behaviour like cycles can also be observed.
7 CONCLUSIONS AND
PERSPECTIVES
In this paper, we introduced a path planning algorithm
for map based localization. First of all, we derived an
information gain as the determinant of the Fisher In-
formation Matrix adapted to multiple features. A geo-
metric interpretation of this measure was made. Then,
to determine the optimal path, we considered the in-
tegral cost of this function. It is important to notice
that the cost computation take into account the sensor
field of view model. Finally, we applied the approach
on a scenario and illustrate the behaviour of the algo-
rithm. We detailed the approach for only the first part
of the total cost, but it can be generalized to the oth-
ers. Now, we plan to take into account noisy feature
positions which will yieldsto a path planning problem
with uncertain cost. Then, the next challenge is to find
optimal paths which tackle also those uncertainties on
the given map.
REFERENCES
Celeste, F., Dambreville, F., and Le Cadre, J.-P. (2007). Op-
timal strategies based on the cross entropy method. In
Fusion 2007, Quebec (Canada).
Gu, G., Chandler, P., Schumacher, C., Sparks, A., and
Pachter, M. (2006). Optimal cooperating sensing us-
ing a team of uavs. IEEE Trans. on Aerospace and
Electronic Systems, 42(4).
Paris, S. and Le Cadre, J.-P. (2002). Trajectory planning for
terrain-aided navigation. In Fusion 2002.
S. Thrun, D. Fox, W. B. and Dellaert, F. (2000). Robust
monte carlo localization for mobile robots. Artificial
Intelligence, 28(1-2):99–141.
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
Robotics. MIT press.
Van Trees, H. (1968). Detection, Estimation and Modula-
tion Theory. New York Wiley.
PATH PLANNING FOR MULTIPLE FEATURES BASED LOCALIZATION
219
