NEAR OPTIMUM CONTROL OF A FULL CAR

ACTIVE SUSPENSION SYSTEM

Paolo Lino and Bruno Maione

Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, via Re David 200, 70125, Bari, Italy

Keywords:

Active suspension, Suspension control, Virtual prototyping, Near-optimum control, AMESim



Abstract:

In this paper, a near-optimum control strategy applied to a full car model equipped with an active suspension

system is presented. The control law is based on a reduced order model obtained by means of a modal

aggregation method, achieving a compromise between computational effort in deriving the control law and

system performances. To assess the controller performances, a virtual prototype of the suspension system is

developed by using AMESim, an advanced ﬂuid-mechanic developing tool. The virtual prototype could be

assumed as a reliable model of the real system enabling to perform safer and cheaper tests than using the real

system. Simulation results show the effectiveness of the approach.

1 INTRODUCTION

A vehicle suspension system mainly aims to carry

the car and its weight, control the vehicle direction

of travel, keep the tires in contact with the road, and

reduce the effect of shock forces due to road distur-

bances, braking and entries into curves. Handling and

ride comfort can be signiﬁcantly improved by using

active suspension systems instead of passive or semi-

active suspensions. More in details, passive suspen-

sion systems include spring and dampers character-

ized by static input-output relationships; semi-active

suspensions use dampers with a variable damping co-

efﬁcient; active suspensions apply a force on car body

and wheels by means of an activeactuator. The design

process of control systems for active and semi-active

suspensions is usually carried on by considering quar-

ter car or half car models. The former only represents

the vertical motion of the car body, the latter includes

pitch or roll motions. Full car models give a more

detailed representation of the car dynamics by includ-

ing vertical displacement, pitch and roll dynamics at

the same time. Different approaches to active suspen-

sions control have been investigated by researchers,

which are mainly based on fuzzy logic, adaptive con-

trol, LQR control and H

∞

control, see (Yoshimura

et al., 1997; Yoshimura et al., 1999; Huang and Lin,

2003; Al-Holou et al., 2002; Fialho and Balas, 2002;

Alleyene and Hedrick, 1995; Hrovat, 1997) and the

references therein.

The main drawback in using lower order models is

that interactions between suspensions are neglected,

so that the control action cannot compensate angu-

lar accelerations or sensibly improve stability. On the

other hand, using simpliﬁed models makes the con-

troller design easier. In this paper, a compromise

between computational effort, detail in representing

the system behaviour and controller performances is

achieved by applying a near-optimum control strategy

to a full car model equipped with an active suspension

system. The controller performances are assessed by

a virtual prototype of the suspension system. The vir-

tual prototype could be assumed as a reliable model of

the real system enabling to perform safer and cheaper

tests than using the real system. Moreover, the inte-

gration of design and optimization processes of both

mechanical and control subsystems are made easier

by taking into account mutual interactions (Lino and

Maione, 2007), thus reducing the whole design effort.

The proposed design process consists in few steps.

Firstly, a 14

order full car analytical model is de-

veloped, representing vertical car body and wheels

motion, as well as pitch and roll angles dynamics.

Then, a reduced order model is derived by applying

a modal aggregation technique and used to develop

a near-optimum control strategy. Finally, the virtual

prototype of suspension system is built to validate the

controller performances.

The paper is organized as follows. Sections 2

and 3 describe the full car analytical model and the

virtual prototype of suspension system, respectively.

The near-optimum control strategy is then introduced

in Section 4. Some simulation results concerning the

controlled system are shown in Section 5. Finally,

Lino P. and Maione B. (2008).

NEAR OPTIMUM CONTROL OF A FULL CAR ACTIVE SUSPENSION SYSTEM.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 46-52

DOI: 10.5220/0001498200460052

 SciTePress

Section 6 gives some conclusions.

2 DYNAMICAL MODEL OF THE

FULL CAR SUSPENSION

SYSTEM

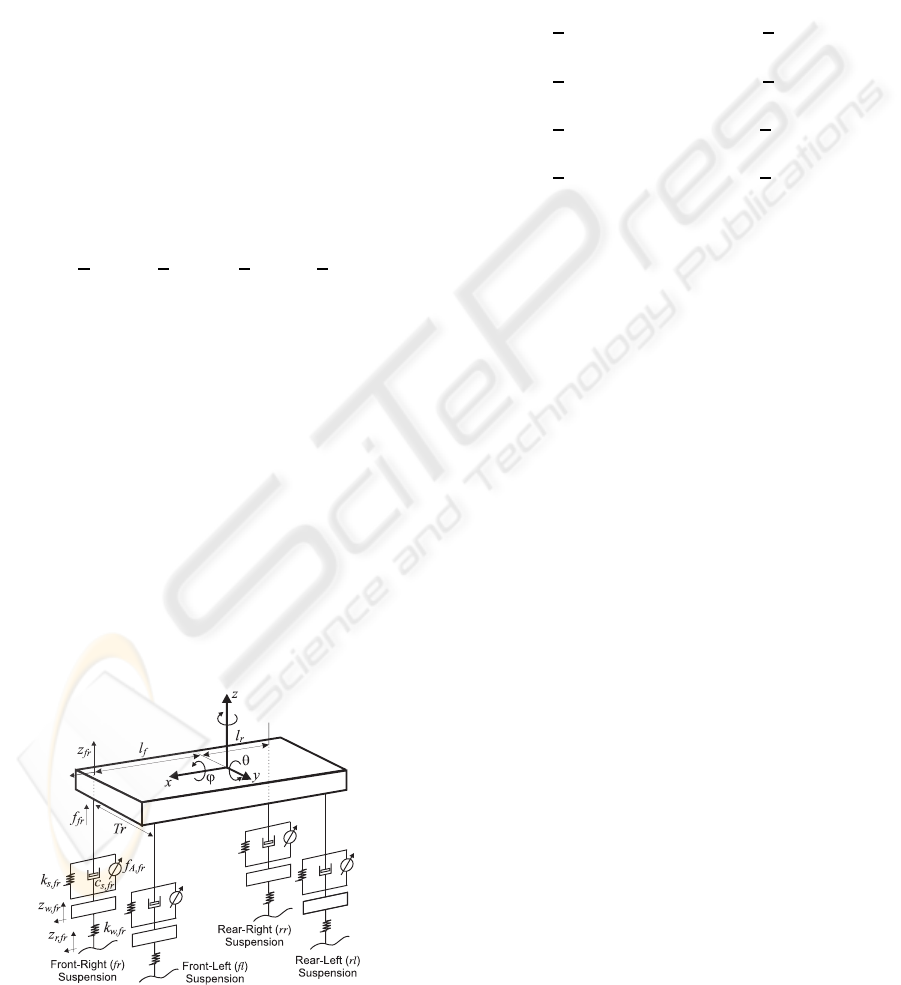
The full car model of a suspension system represents

the vehicle as a rigid body with seven degrees of free-

dom, which originate from translation motion along

axes, as well as rotational motions, i.e. pitch and

roll motions around center of gravity (COG) (Ikenaga

et al., 2000).

With reference to Fig. 1, by setting COG of the

car body as origin of axes, the vehicle body dynamics

can be described by the following equations:











¨z = f

+ f

θ = − f

+ f

φ =

Tr−

Tr+

(1)

where z is the vertical displacement of car body COG,

, f

are the forces applied by front-left,

front-right, rear-left, rear-right suspensions on the car

body, respectively, θ and φ are the pitch and roll an-

gles, respectively, l

and l

are the distances from the

front and rear axles to car body COG, Tr is the wheels

track, m

is the car body mass, I

and I

are the pitch

and roll moments of inertia of the car body, respec-

tively.

The force applied to the car body by each suspen-

sion can be computed as in the following:











= k

s,i

w,i

− z

) + c

s,i

(˙z

w,i

− ˙z

) + f

A,i

w,i

¨z

w,i

= −k

s,i

w,i

− z

) − c

s,i

(˙z

w,i

− ˙z

− k

w,i

− z

r,i

) − f

A,i

(2)

Figure 1: Vertical body model of the full car suspension

system.

where subscript i ∈ { fl, fr, rl,rr} characterizes the

four suspensions, z

w,i

and z

are the vertical displace-

ments of the wheel COG and car body corner, respec-

tively, m

w,i

is the wheel mass, k

s,i

and c

s,i

are the stiff-

ness and damping factor of the suspension, respec-

tively, k

w,i

is the wheel stiffness, and f

A,i

is the active

force applied by the controlled actuator.

The following equations express the vertical dis-

placement of car body corners in terms of z, θ and

φ:

= z+

Tr· sinφ − l

sinθ ≈ z+

Tr· φ− l

= z−

Tr· sinφ − l

sinθ ≈ z−

Tr· φ− l

= z+

Tr· sinφ + l

sinθ ≈ z+

Tr· φ+ l

= z−

Tr· sinφ + l

sinθ ≈ z−

Tr· φ+ l

(3)

where the approximations hold for small variations of

pitch and roll angles. Combining equations (1), (2)

and (3) results in a system of differential equations of

the form:











¨z

= f

, ˙z

w,i

, ˙z

w,i

,φ,

φ,θ,

θ, f

A,i

)

θ = f

, ˙z

w,i

, ˙z

w,i

,φ,

φ,θ,

θ, f

A,i

)

φ = f

, ˙z

w,i

, ˙z

w,i

,φ,

φ,θ,

θ, f

A,i

)

(4)

Equations (4), together with those of wheels vertical

displacements:

¨z

w,i

= f

4,i

, ˙z

w,i

, ˙z

w,i

r,i

,θ,

θ,φ,

φ, f

A,i

) (5)

represent the full car dynamics under the action of

road disturbances and actuation forces. The design of

a control law can be simpliﬁed by putting equations

(4) and (5) in a state space form:

x = Ax+ Bf+ Hd, (6)

where f = [ f

A, fl

, f

A, fr

, f

A,rl

, f

A,rr

]

is the vector of ac-

tuation forces, d = [z

r, fl

r, fr

r,rl

r,rr

]

is the vector

of road disturbances, and x is the state vector, com-

posed of vertical displacements, pitch and roll angles

and its derivatives.

A more accurate model of the suspension system

includes the actuators dynamics. In this paper, the hy-

draulic actuator described in (Rajamani and Hedrick,

1995) is considered. It consists of a cylinder with a

moving piston pushed by the pressure difference on

its upper and lower surfaces (Fig. 2).

The pressure difference is regulated by an elec-

tronic valve driven by the control system. Under the

assumption of a negligible piston inertia with respect

to high hydraulic forces, the actuation force is given

by:

A,i

= −A

y,i

(˙z

c,i

− ˙z

w,i

) + u

, (7)

NEAR OPTIMUM CONTROL OF A FULL CAR ACTIVE SUSPENSION SYSTEM

Figure 2: Hydraulic actuator for active suspensions.

where u is a linear function of the control pressure set

by acting on the electronic valve, and A

y,i

is a con-

stant parameter depending on the system geometry

and working ﬂuid characteristics. By suitably intro-

ducing an E matrix, the system state space model be-

comes:

x = (A+ BE)x+ Bu+ Hd, (8)

where u is the vector of control inputs u

3 VIRTUAL PROTOTYPE OF THE

SUSPENSION SYSTEM

As virtual environment for design integration, we

use AMESim



(Advanced Modelling Environment

for Simulation): a simulation tool, which is oriented

to lumped parameter modelling of components from

different physical domains, interconnected by ports

enlightening the energy exchanges between element

and element and between an element and its environ-

ment. It also guarantees a ﬂexible architecture, capa-

ble of including new components deﬁned by the users

(IMAGINE S.A., 2004).

The AMESim virtual prototype (Fig. 3) used to

evaluate the controller performances has been devel-

oped by employing the AMESim-Simulink interface

in Co-simulation mode: each suspension-wheel sub-

system is modelled within the AMESim environment;

the car body dynamical equations (1) are solved using

MATLAB. AMESim and Simulink cooperate by inte-

grating the relevant portions of models.

The main components of each suspension-wheel

subsystem are the Mass block with stiction and

coulomb friction and end stops, which computes the

wheel dynamics through the Newtons second law of

motion, the Mechanical spring and dumper comput-

ing the elastic and damping forces of suspensions and

wheels depending on nonlinear stiffness and damping

coefﬁcients, the Piston with moving body, represent-

ing the actuator hydraulic circuit dynamics and com-

puting the pressure forces acting upon the upper and

lower piston surfaces, and the 3 positions hydraulic

control valve modelling the electro-hydraulic circuit

driving the actuator.

The pressure dynamics inside cylinders are com-

puted as a function of intake and outtake ﬂows Q

out

, as well as of volume changes due to mechanical

part motions, according to the following equation:



− Q

+ Q

out



, (9)

where P and ρ are the working ﬂuid pressure and den-

sity, respectively, and v is the taken up volume. Q

and Q

out

can be calculated by applying the energy

conservation law, which gives, for a generic Q:

Q = c

(ρ,η)Aρ

2|∆P|

sgn(∆P), (10)

where ∆P is the working ﬂuid pressure difference

across the ﬂow section A; sgn(∆P) is the sign func-

tion affecting the ﬂow direction; the discharge coefﬁ-

cient c

accounts for nonuniform ﬂow rates and ﬂow

process non-isentropicity, depending on ﬂuid density

ρ and cinematic viscosity η. Finally, the 3 positions

hydraulic control valve block models the controlled

valve as a second order spring-damp linear system.

To take into account the inﬂuence of inertia on

pitch and roll dynamics during brakes and entries into

a curve, the following equations are included in the

model:



θ = m

¨x

φ = m

¨y

, (11)

where h

is the distance from the contact point be-

tween wheel and suspension to car body COG, and ¨x

and ¨y are the COG accelerations along x and y axes,

respectively.

4 THE NEAR-OPTIMUM

CONTROL STRATEGY

Given a system described by the state space equa-

tions:

˙x(t) = Ax(t) + Bu(t), x(0) = x

y(t) = Dx(t)

(12)

and a quadratic cost function:

J =

∞



x(t)

Qx(t) + u(t)

Ru(t)



dt, (13)

being Q and R two positive semi-deﬁnite matrices,

it is well known that the Linear-Quadratic-Regulator

(LQR) problem consists in ﬁnding an input vector

∗

(t) = −Kx(t) minimizing the cost function J via

state-feedback (Dorato et al., 2000). The state feed-

back matrix K can be computed as:

K = R

−1

P, (14)

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

Figure 3: AMESim virtual prototype of the full car suspension system.

where P is the solution of the following matrix Riccati

equation:

P+ PA− PBR

−1

P+ Q = 0. (15)

Q and R matrices can be considered as weights on

state and control input, respectively, and affect the

value assumed by elements of matrix K. The Riccati

equation complexity directly depends on the system

order and its solution requests n(n + 1)/2 operations.

For a high order system it calls for a large compu-

tational effort, which could not be sustainable for on

line calculations; a solution consists in adopting large

scale system techniques to reduce problem complex-

ity and make the application of optimal control theory

easier (Jamshidi, 1983). These approaches, which are

based on reduction of order, perturbation of parame-

ters, decomposition of structure, hierarchical interac-

tion or decentralization of control, lead to near opti-

mality of system performance.

In this paper, the aggregation method based on the

modal approach is applied to reduce the model or-

der (Jamshidi, 1983). More in details, it neglects the

effect of non dominant modes to obtain a system of

aggregated states

ζ:

ζ(t) = Fζ(t) + Gu(t),ζ(0) = ζ

y(t) = Lζ(t)

(16)

by using a transformation matrix C:

ζ(t) = Cx(t), ζ(0) = Cx(0). (17)

The reduced order model matches the full order

model dynamics if the dynamic exactness condition

holds:

FC = CA

G = CB

LC = D.

(18)

By deﬁning an error vector e(t) = ζ(t)−Cx(t), its dy-

namics is described by the equation

e = Fe+ (FC−

CA)x+ (G− CB)u, which reduces to

e = Fe if con-

ditions (18) hold. Provided that F is a positive deﬁnite

matrix, error reduces to 0 even for e(0) 6= 0.

To derive the aggregation matrix C, the modal ap-

proach exploits the system modal matrix M, whose el-

ements are the eigenvectors of state matrix A. Hence,

if arranging columns of matrix M by starting from

eigenvectors related to slowest dynamics, the reduced

order system matrices can be obtained using the fol-

lowing relationships:

F = M

SΛS

−1

C = M

−1

G = CB

L ≈ DC

(19)

where M

is the nonsingular leading principal minor

of matrix M of order l, S = [I

0], being I

the Iden-

tity matrix, Λ is the Jordan matrix of A, and C

is the

pseudo-inverse of C.

NEAR OPTIMUM CONTROL OF A FULL CAR ACTIVE SUSPENSION SYSTEM

Considering the reduced order system, the Riccati

equation becomes:

+ P

− P

−1

+ Q

= 0, (20)

so that the following control action is obtained:

(t) = −R

−1

ζ(t) = −R

−1

Cx(t)

= −K

x(t)

(21)

By pre- and post- multiplying eq. (20) by C

and C,

respectively, and considering the aggregation condi-

tions, it is straightforward to obtain:

C) + (C

C)A+

− (C

C)BR

−1

C) + C

C = 0.

(22)

Equations (15) and (22) coincide provided that the

following positions hold:

P = C

Q = C

(23)

Hence, the Q

matrix can be obtained as:

= (CC

)

−1

CQC

(CC

)

−1

. (24)

Finally, K

matrix is obtained from F, G, Q

and R

matrices.

In this paper, a 6

order aggregated model is de-

rived from the full order suspension system and used

to derive the control law.

5 SIMULATION RESULTS

To evaluate the controller performances, a set of tests

is performed on the virtual prototype by applying

different road proﬁles. In particular, the following

benchmarks used in industrial practice are considered

(Canale et al., 2006):

•

Sine wave hole

proﬁle: a sine proﬁle hole with

0.03 m of amplitude and 6 m of width; for the

sake of brevity, only 30 and 90 Km/h car speeds

are considered in this paper;

•

Short back

proﬁle: a positive step of road proﬁle

with 0.02 m of amplitude and 0.5 m of width, with

a travelling speed of 30 Km/h;

•

Drain well

proﬁle: a negative step variation of

road proﬁle with 0.05 m of amplitude and 0.6 m

of width, with a traveling speed of 30 km/h.

Moreover, the system response in case of entry in

a curve or braking is analysed. The proposed con-

troller performances have been compared with those

obtained by using an active decoupled controller (Ike-

naga et al., 2000) and an LQR controller based on the

full order model. In particular, the control scheme

proposed in (Ikenaga et al., 2000) includes a ride con-

trol loop, for road disturbances rejection, and an atti-

tude control loop, for roll, pitch and vertical dynam-

ics regulation. To former includes an active ﬁltering

feedback, the latter is based on a sky-hook control

strategy. A decoupling is performed to deal with the

under-actuation problem.

Figure 4 shows pitch and vertical displacement

dynamics when applying the sine wave hole road pro-

ﬁle. Since the road disturbance is symmetrically ap-

plied to left and right wheels, the roll dynamics is neg-

ligible and not displayed.

It is evident that the LQR controller guarantees

better performances than the near-optimum and the

decoupled controllers, in terms of overshoot and set-

tling time. Nevertheless, the near optimum controller

allows acceptable pitch angle and vertical displace-

ment dynamics, improving the results obtained with

the decoupled controller.

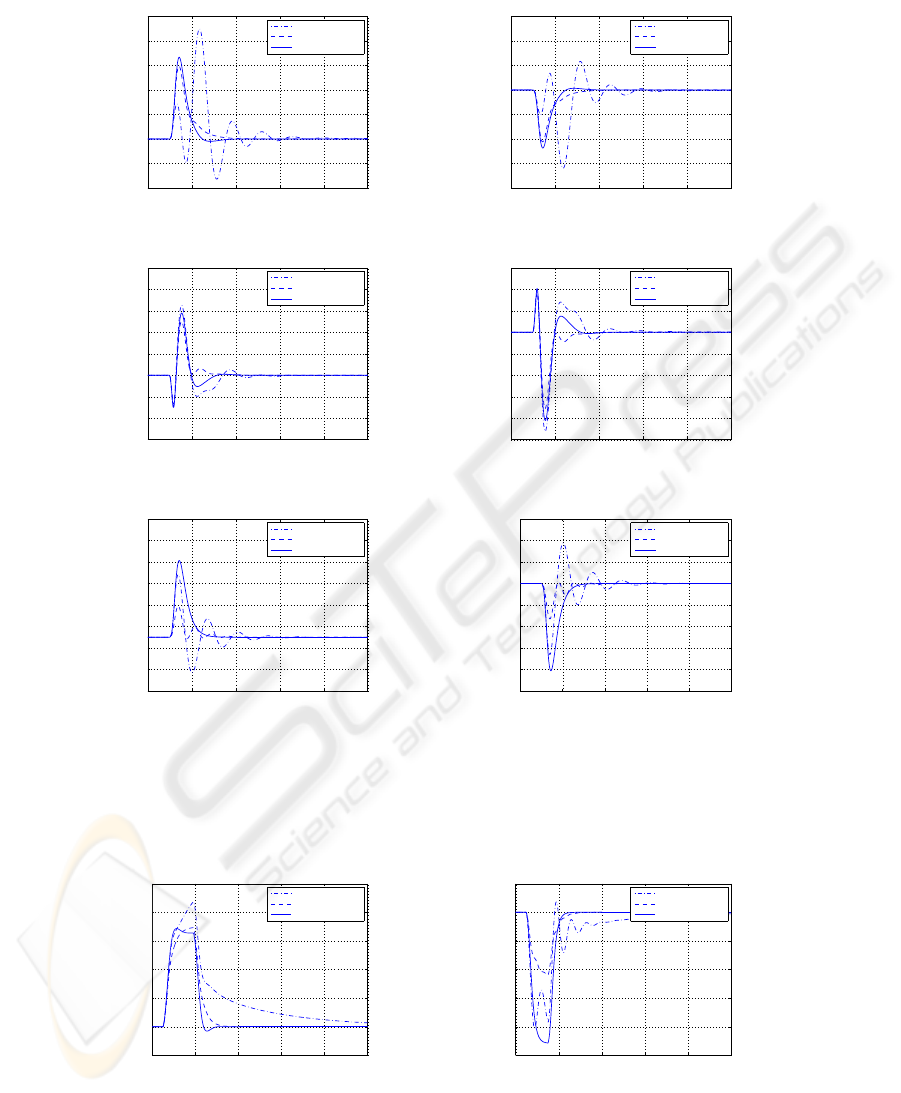
In Figure 5, the drain well and the short back

disturbances are only applied to left wheels, so that

the roll angle dynamics is excited. Simulation results

show that the LQR controller still guarantees a better

system behaviour for all conditions thanks to a prompt

control action, while the near-optimum controller im-

proves results obtained with the decoupled controller.

Finally, Figure 6 displays the effect of sudden

longitudinal and lateral accelerations determined by

braking (Fig. 6(a)), and entry into a curve (Fig. 6(b)),

which independently affect the pitch dynamics and

the roll dynamics, respectively.

In the former case, the near-optimum and the LQR

controllers show similar performances; in the latter

case, the near-optimum controller cannot reduce sig-

niﬁcantly the roll angle overshoot. In general, the

decoupled controller cannot guarantee fast transients

due to actuator saturation; the near optimum and

LQR controller can suitably restrain the control ac-

tion thanks to a suitable choice of the performance in-

dex weights. To sum up, the near optimum controller

represents a compromise in terms of system perfor-

mances and complexity, while the LQR controller al-

ways shows the best performances.

6 CONCLUSIONS

In this paper, a near-optimum control strategy applied

to a full-car active suspension system has been pro-

posed. The design process relies on the use of a high

order analytical model, from which an aggregated low

order model is derived, and of a virtual prototype de-

veloped by using the AMESim simulation package.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

0 1 2 3 4 5

−0.025

−0.02

−0.015

−0.01

−0.005

0.005

Sine Wave Hole 30 Km/h

Time [s]

Heave Position [m]

Decoupled C.

Optimal C.

Near−optimum C.

(a)

0 1 2 3 4 5

−0.025

−0.02

−0.015

−0.01

−0.005

0.005

Sine Wave Hole 90 Km/h

Time [s]

Heave Position [m]

Decoupled C.

Optimal C.

Near−optimum C.

(b)

0 1 2 3 4 5

−2.5

−2

−1.5

−1

−0.5

0.5

1.5

x 10

−3

Sine Wave Hole (30 Km/h)

Time [s]

Pitch Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(c)

0 1 2 3 4 5

−2.5

−2

−1.5

−1

−0.5

0.5

1.5

x 10

−3

Sine Wave Hole (90 Km/h)

Time [s]

Pitch Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(d)

Figure 4: Vertical displacement (a)-(b) and Pitch angle (c)-(d) dynamics for a sine wave hole road proﬁle ran at 30 km/h and

90 km/h, respectively.

The virtual prototype represents a reliable benchmark

for evaluating the controller performances before the

implementation on the real system. Moreover, it can

be used for the integrated design of both mechanical

and control subsystems at the same time. As simula-

tion experiments have shown, the proposed controller

provides good performances, despite the low compu-

tational effort required.

REFERENCES

Al-Holou, N., Lahdhiri, T., Joo, D., Weaver, J., and

Al-Abbas, F. (2002). Sliding mode neural net-

work inference fuzzy logic control for active suspen-

sion systems. IEEE Transactions on Fuzzy Systems,

10(2):234–246.

Alleyene, A. and Hedrick, J. (1995). Nonlinear adaptive

control of active suspensions. IEEE Transactions on

Control Systems Technology, 3(1):94–101.

Canale, M., Milanese, M., and Novara, C. (2006).

Semi-Active Suspension Control Using ’Fast’ Model-

Predictive Techniques. IEEE Transactions on Control

Systems Technology, 14(6):1034–1046.

Dorato, P., Abdallah, C., and Cerone, V. (2000). Linear

Quadratic Control: An Introduction. Krieger Publish-

ing Company, Melbourne.

Fialho, I. and Balas, G. (2002). Road adaptive active sus-

pension design using linear parameter-varying gain-

scheduling. IEEE Transactions on Control Systems

Technology, 10(1):43–54.

Hrovat, D. (1997). Survey of Advanced Suspension Devel-

opments and Related Optimal Control Applications.

Automatica, 33(10):1781–1817.

Huang, S. and Lin, W. (2003). Adaptive fuzzy controller

with sliding surface for vehicle suspension control.

IEEE Transactions on Fuzzy Systems, 11(4):550–559.

Ikenaga, S., Lewis, F., Campos, J., and Davis, L. (2000).

Active suspension control of ground vehicle based on

a full-vehicle model. In ACC 2000, Proceedings of the

2000 American Control Conference.

Jamshidi, M. (1983). Large-Scale Systems: Modeling and

Control. Elsevier Science Ltd, Amsterdam.

Lino, P. and Maione, B. (2007). Integrated design of a

mechatronic system - the pressure control in common

rails. In ICINCO 2007, Proceedings of the Fourth In-

ternational Conference on Informatics in Control, Au-

tomation and Robotics, Angers, France.

Rajamani, R. and Hedrick, J. (1995). Adaptiver Observers

for Active Automotive Suspensions: Theory and Ex-

periment. IEEE Transactions on Control Systems

Technology, 3(1):86–93.

IMAGINE S.A. (2004). AMESim User Manual v4.2.

Roanne, France.

Yoshimura, T., Isari, Y., Li, Q., and Hino, J. (1997). Active

suspension of motor coaches using skyhook damper

and fuzzy logic control. Control Engineering Prac-

tice, 5(2):175–184.

Yoshimura, T., Nakaminami, K., Kurimoto, M., and Hino,

J. (1999). Active suspension of passenger cars using

linear and fuzzy-logic controls. Control Engineering

Practice, (7):41–47.

NEAR OPTIMUM CONTROL OF A FULL CAR ACTIVE SUSPENSION SYSTEM

0 1 2 3 4 5

−1

−0.5

0.5

1.5

2.5

x 10

−3

Short back

Time [s]

Heave Position [m]

Decoupled C.

Optimal C.

Near−optimum C.

(a)

0 1 2 3 4 5

−8

−6

−4

−2

x 10

−3

Drain well

Time [s]

Heave Position [m]

Decoupled C.

Optimal C.

Near−optimum C.

(b)

0 1 2 3 4 5

−2

−1

x 10

−4

Short back

Time [s]

Pitch Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(c)

0 1 2 3 4 5

−10

−8

−6

−4

−2

x 10

−4

Drain well

Time [s]

Pitch Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(d)

0 1 2 3 4 5

−5

−3

−1

x 10

−3

Short back

Time [s]

Roll Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(e)

0 1 2 3 4 5

−0.025

−0.02

−0.015

−0.01

−0.005

0.005

0.01

0.015

Drain well

Time [s]

Roll Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(f)

Figure 5: Vertical displacement, pitch angle and roll angle dynamics when applying short back and drain well road distur-

bances; (a)-(c)-(e) short back disturbance applied ; (b)-(d)-(f) drain well disturbance applied.

0 2 4 6 8 10

−0.02

0.02

0.04

0.06

0.08

0.1

Braking

Time [s]

Pitch Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(a)

0 2 4 6 8 10

−0.1

−0.08

−0.06

−0.04

−0.02

0.02

Entrance into curve

Time [s]

Roll Angle [rad]

Decoupled C.

Optimal C.

Near−optimum C.

(b)

Figure 6: Pitch angle (a) and roll angle (b) dynamics in case of braking and entry into a curve, respectively.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics