DCT DOMAIN VIDEO WATERMARKING

Attack Estimation and Capacity Evaluation

O. Dumitru, M. Mitrea and F. Prêteux

Institut TELECOM / TELECOM & Management SudParis, ARTEMIS Departement, France

Keywords: DCT video watermarking, capacity, attack, pdf estimation, Gaussian mixtures.

Abstract: The first difficulty when trying to evaluate with accuracy the video watermarking capacity is the lack of a

reliable statistical model for the malicious attacks. The present paper brings into evidence that the attack

effects in the DCT domain are stationary and computes the corresponding pdfs. In this respect, an in-depth

statistical approach is deployed by combining Gaussian mixture estimation with the probability confidence

limits. Further on, these pdfs are involved in capacity computation. The experimental results are obtained on

a corpus of 10 video sequences (about 25 minutes each), with heterogeneous content.

1 INTRODUCTION

For property right identification purposes, the

watermarking techniques insert a mark into some

original media (e.g. a video). If the mark insertion

does not result in visual artefacts, the method

features transparency. If a pirate cannot eliminate

the mark without damaging the marked video, the

method features robustness (Cox & others, 2002).

In practice, the better the robustness, the worse

the transparency. In order to reach a balance

between these two constraints, the mark is inserted

into some spectral representations of the original

data, e.g. in the DCT (Discrete Cosine Transform).

A crucial issue is to compute the watermarking

capacity, i.e. the largest amount of information

which can be inserted into a video, for prescribed

transparency and robustness. The watermarking

capacity is computed as the capacity of the noisy

channel modelling the watermarking method,

Figure 1. According to this model, the mark is

sampled from the information source. The detection

is impaired by the noise sources: the original video

itself and the attacks. The side information

watermarking exploits the fact that the original video

is known at the insertion but unknown at the

detection. As such a noise source should not

decrease the channel capacity (Costa, 1983), the

attacks remain the restricting factor and their

intimate knowledge would grant accuracy in

capacity evaluation. The present paper focuses on

some real life attacks and models their effects in the

DCT domain. Note that attack modelling is not a

trivial task. Actually, any mathematical approach

should properly answer at least the following

questions:

1. Does a general statistical model for the

considered attack effects, independent with

respect to the video sequence, really exist?

2. When considering an individual video sequence,

does a reliable model exist for any (intra)frame

content and any (inter)frame dependency?

Positive answers at these first questions mean a

proof of stationarity concerning the attacks.

3. In case such a model exists, which is its pdf

(probability density function)? Although the

Gaussian law is generally considered, previous

studies rejected this popular assumption.

Figure 1: The watermarking model.

The paper has the following structure. After

having defined a set of random variables

corresponding to the attack effects, Section 2

presents the statistical investigation procedure.

Section 3 describes the experimental results. The

capacity evaluation is dealt with in Section 4 while

Section 5 concludes the paper. The Appendix

summarises some theoretical bases.

Channel

mar

original video

attack

mark

detection

239

Dumitru O., Mitrea M. and Prêteux F. (2008).

DCT DOMAIN VIDEO WATERMARKING - Attack Estimation and Capacity Evaluation.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 239-244

DOI: 10.5220/0001498302390244

 SciTePress

2 INVESTIGATION PROCEDURE

2.1 Attack Effect Representation

Be there an L frame colour video. Each frame is

represented in the HSV space. The following steps

are applied to each frame (Mitrea & others, 2006):

 Compute the DCT on the original V component.

 Decreasingly sort the coefficients and record the

largest

values in a vector

n ; record their

corresponding locations in a vector

l .

 Apply the DCT to the attacked

V component and

record the coefficients at the l locations into the

new vector, denoted by

n .

 Compute the vector:

nndifference −= .

A set of

L vectors of the same type as difference

(each of them with

R components) is thus obtained.

Be noise a vector with L components,

containing the values corresponding to an arbitrarily

chosen rank

r in the set of difference vectors:

],...,,[

21 L

nnnnoise = . Such a vector is sampled

from a random variable modelling the attack effects

in the

rank of the DCT hierarchy. To model the

attacks means to obtain the

pdf for the corresponding

random variable (a model for each rank).

2.2 Pdf Estimation for Attacks

There are many pdf estimation tools based on iid

(independent and identically distributed) data, but

thiey do not apply here. The

noise vector is

computed on successive (dependent) frames and the

a priori lack of support for attack stationarity can

raise suspicions about the data identical distribution.

Hence, a general estimation procedure should be

considered (Mitrea & others, 2007):



Eliminate the data dependency. Sample the

],...,,[

21 L

nnnnoise = vector with a D period.

Shift the sampling origin and get

D iid data sets

],...,,[],...,,[

)1(

iDNiDi

iii

nnnxxx

+−+

= ,

where

Di ,...,2,1=

and

DLN /= .

 Extract partial information from each iid data

set.

Obtain )(

( Di ,...,2,1

) by Gaussian

mixture estimation (Appendix).

 Extract global information. Apply the Gaussian

mixture estimation to the

noise vector and obtain

)(

(an average model).

 Define the model. First, define a similarity

measure between two

pdfs, eq. (1):

∑

∫

∑

∫

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

dxxv

dxxvxu

xvxum

)(

))()((

))(),((

(1)

where

I , Ss ,...2,1

is a subdivision of the

];[

maxmin

xx interval on which the u and

pdfs take non-zero values. Secondly, define the

attack model as

(.)

p which is the iid estimate

closest to the

(.)

p in the (.)m sense:

))(

),(

(minarg)(

xpxpmxp

= .

(2)

 Evaluate the model accuracy. Calculate the

average similarity measure between each of the

D pdfs and the (.)

p model, eq. (3):

∑

xpxpm

Error

))(

),(

(

(3)

If this procedure is successful when applied to an

individual video (Section 3.1), then positive answers

to the last two questions in the Introduction are

obtained. A positive answer to the first question is

obtained iff. the same model is obtained for different

video sequences (Section 3.2).

3 EXPERIMENTAL RESULTS

The corpus contains 10 video sequences (64 Kbit/s),

each of them of

35000

L frames (about 25

minutes each). The content is heterogeneous,

combining film, news, and home video excerpts.

The frame size is

80192 × pixels. The V

component is normalised to the

]1,0[

interval. The

DCT is individually applied to whole frames, and

the largest

360

R coefficients are investigated.

3.1 Model Computation

The model is computed for an arbitrarily chosen

video sequence. The following parameters are

considered:

250

D frames (i.e. 10s); 10=K pdfs

in the mixture;

200

iter

N iterations in the EM

algorithm;

S evenly distributed intervals.

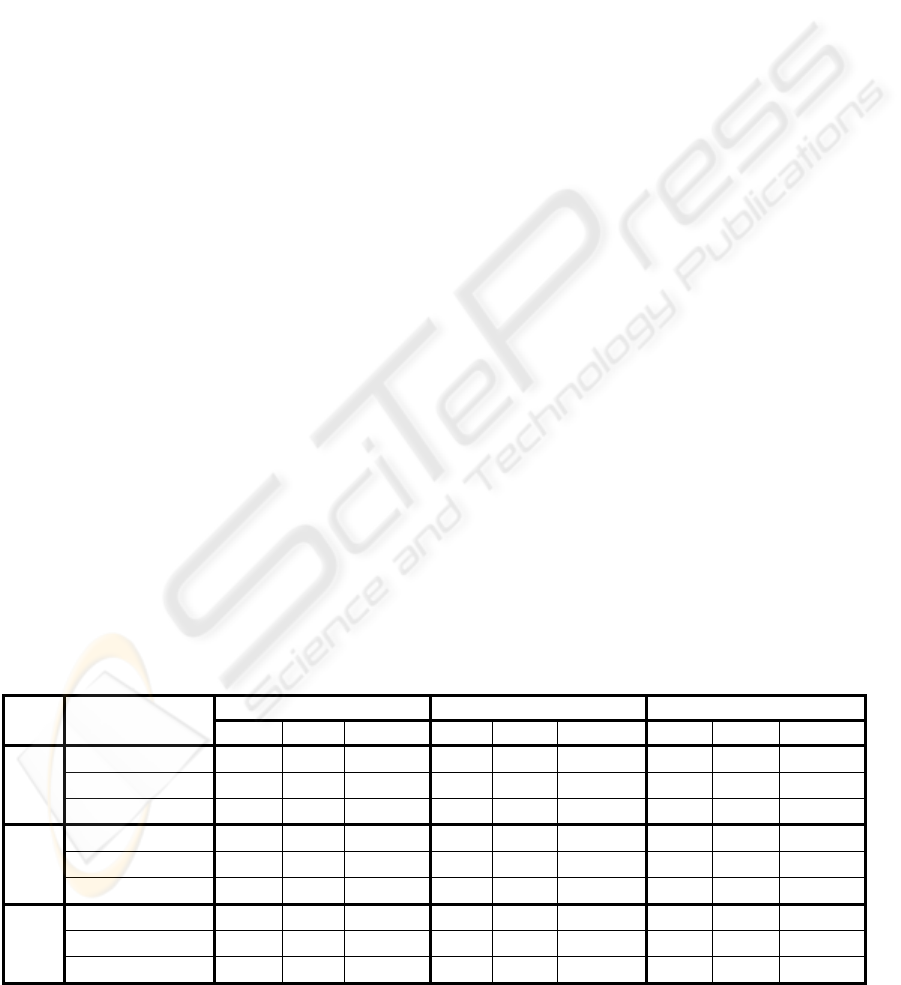
Table 1 presents the models for three ranks (1,

150, 300) and three attacks (Gaussian filtering,

sharpening, and StirMark). In each case, the

)(

model is computed according to (2), its the

parameters (

,),( ) according to (A3) and

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

240

the corresponding errors to (3). Notice that each and

every time, the

Error values are lower than 0.04.

In order to illustrate the results in Table 1,

Figure 2 depicts in continuous line the models for

one rank (

300=r ) and the three attacks. For

comparison, Figure 2 also represents (in dashed line)

the Gaussian

pdf with the same mean values and

variances as the computed models.

The same results were obtained for each of the

10 video sequences in the corpus and for each

investigated attack: the parameters were slightly

different but the errors were lower than 0.05.

The models, for all 360 ranks and for other

attacks (Frequency Model Laplacian Removal,

median filtering, small rotations, JPEG compression)

can be obtained by contacting the authors.

3.2 Model Validation

Up to now, the experimental results point to the

existence of a model for the attack effects on a

particular video sequence and estimate this model

(

i.e. elucidates the second & third questions in the

Introduction).

Table 1: Statistical model for the watermarking attacks in the DCT hierarchy.

Attack

Rank

Model parameters Error

P(k) 0.076 0.072 0.228 0.095 0.021 0.096 0.071 0.133 0.120 0.083

μ(k) 0.274 0.319 0.214 0.305 0.788 0.283 0.330 0.052 0.440 0.374

r = 1

σ(k) 0.110 0.118 0.031 0.116 0.037 0.112 0.108 0.055 0.091 0.112

0.035

P(k) 0.019 0.025 0.190 0.213 0.091 0.075 0.271 0.025 0.031 0.056

μ(k) 0.224 0.195 0.031 0.009 0.072 0.121 0.063 0.101 0.201 0.131

r=150

σ(k) 0.130 0.135 0.011 0.021 0.083 0.010 0.010 0.110 0.134 0.046

0.013

P(k) 0.080 0.044 0.048 0.146 0.056 0.038 0.041 0.284 0.093 0.164

μ(k) 0.131 0.096 0.094 0.066 0.083 0.091 0.090 0.023 0.062 0.055

Gaussian filtering

r=300

σ(k) 0.053 0.112 0.111 0.025 0.069 0.110 0.110 0.012 0.026 0.029

0.013

P(k) 0.319 0.057 0.083 0.066 0.095 0.056 0.101 0.073 0.074 0.071

μ(k) -1.478 -1.185 -2.325 -2.151 -2.341 -0.971 -2.424 -0.536 -2.347 -2.141

r = 1

σ(k) 0.284 0.789 0.557 0.604 0.551 0.747 0.441 0.648 0.549 0.606

0.020

P(k) 0.102 0.029 0.091 0.033 0.171 0.033 0.140 0.081 0.155 0.159

μ(k) -0.324 0.213 -0.124 -1.104 -0.080 -0.716 -0.063 -0.279 -0.078 -0.035

r=150

σ(k) 0.137 0.028 0.102 0.316 0.103 0.168 0.103 0.150 0.104 0.098

0.021

P(k) 0.054 0.151 0.283 0.105 0.078 0.067 0.073 0.098 0.023 0.063

μ(k) -0.211 -0.105 -0.106 -0.114 -0.369 -0.030 -0.115 -0.120 -0.905 -0.203

Sharpening

r=300

σ(k) 0.180 0.096 0.095 0.156 0.133 0.133 0.156 0.158 0.155 0.178

0.021

P(k) 0.070 0.087 0.105 0.116 0.097 0.100 0.059 0.131 0.069 0.161

μ(k) -0.480 0.075 -0.354 -0.289 -0.115 -0.389 -0.401 -0.348 -0.619 -0.150

r = 1

σ(k) 0.368 0.397 0.271 0.263 0.436 0.270 0.404 0.269 0.357 0.215

0.037

P(k) 0.235 0.083 0.043 0.096 0.070 0.149 0.087 0.048 0.075 0.109

μ(k) 0.036 -0.084 0.206 0.103 0.422 0.006 0.017 -0.096 0.092 0.124

r=150

σ(k) 0.084 0.204 0.027 0.063 0.073 0.100 0.136 0.203 0.155 0.146

0.019

P(k) 0.085 0.075 0.046 0.078 0.137 0.036 0.010 0.046 0.300 0.093

μ(k) 0.004 0.191 0.197 -0.003 0.192 0.165 -0.005 0.212 0.047 0.015

StirMark

r=300

σ(k) 0.144 0.193 0.192 0.141 0.074 0.195 0.140 0.189 0.036 0.148

0.018

Gaussian filtering Sharpening StirMark

Figure 2: The attack models (continuous line) and the corresponding Gaussian laws (dashed line) for the rank r=300.

DCT DOMAIN VIDEO WATERMARKING - Attack Estimation and Capacity Evaluation

241

The model independence w.r.t. the video sequence

and the estimation procedure is now to be

investigated.

First, it should be précised whether the model

computed on a particular video sequence can be

representative for the whole corpus or not. In this

respect, the investigation algorithm is resumed on

the rest of 9 video sequences from the corpus and

the corresponding models are computed. The errors

between the reference model and these new models

are evaluated according to three criteria: the

similarity measure in eq. (1), the Kullback-Leibler

divergence and the Hellinger distance (Appendix).

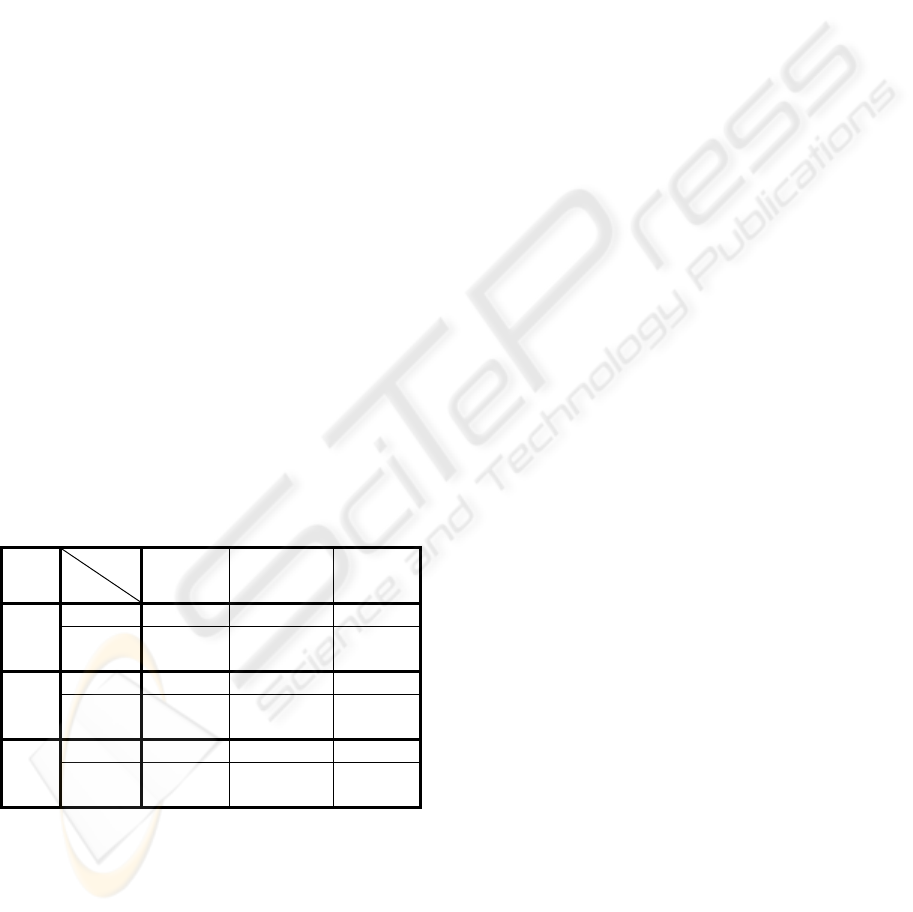
For each criterion, and for three ranks, the minimal,

maximal, and average errors are reported in Table 2.

The numerical values obtained for the distance in

eq. (1) ascertain a quite good accuracy (and

generality) for the model provided in Table 1: the

average errors are acceptably low, with one

exception, namely the Gaussian filtering. The

Kullback-Leibler divergence and the Hellinger

distance lead to acceptably small values for all the

attacks. In order to compute these three measures,

the following instantiations were made in eqs. (1),

(A4) and (A5):

)(xv is the reference pdf while )(xu

is, successively, each of the other 9 individual

models computed on the corpus. The interval

]3,3[

mixmixmixmix

∗+∗−= , where

mix

and

mix

are the mixture mean and variance.

Secondly, the concordance between the

maximum likelihood estimation (which is the basis

for the EM Gaussian mixture algorithm) and the

popular confidence limit estimation is checked. Note

that the EM Gaussian mixture estimation results in a

continuous

pdf while the confidence limit estimation

provides values for the probability that a random

variable takes values in a given interval, but not the

pdf itself. Consequently, the interval where the

Gaussian mixture

model takes non-zero values is

evenly divided into 10 sub-intervals. On the one

hand, confidence limits for the probability that the

noise effects would take values in these sub-intervals

are derived. On the other hand, the integral of the

Gaussian mixture model on the same sub-intervals

are computed. The experiments bring into evidence

that each and every time (

i.e. for each type of

investigated attack and for each rank) the integral on

the EM Gaussian model belongs to the

corresponding confidence limits.

This sub-section shows that an individual model

(Table 1), computed on a particular video sequence,

is valuable for all the video sequences involved in

the experiments and, moreover, that it does not

depend on the estimation procedure. This means a

positive answer to the first question in Introduction.

4 CAPACITY COMPUTATION

As discussed in Introduction, any side-information

watermarking technique can be modelled by a noisy

channel, where the mark is a sample from the

information source and the noise is represented by

the attacks. In order to evaluate the capacity of such

a channel, the eqs. (A7) and (A8) are considered.

For the capacity limits in eq. (A7), the noise power

N is the variance of the noise vector, Section 2.2.

The signal power

P was derived from transparency

constraints, so as to ensure a mark 30dB lower than

the original (unmarked) coefficients.

Table 2: The errors (minimal, maximal, average) between the reference model and the 9 models obtained on different video

sequences, for three ranks:

r = 1, r=150, and r = 300.

r = 1 r = 150 r = 300

Type Attack

Min Max Average Min Max Average Min Max Average

Gaussian filtering 0.662 0.758 0.710 0.058 0.216 0.137 0.071 0.153 0.112

Sharpening 0.109 0.148 0.128 0.028 0.065 0.046 0.055 0.087 0.071

Error

StirMark 0.077 0.093 0.085 0.065 0.109 0.087 0.084 0.131 0.108

Gaussian filtering 0.131 0.204 0.167 0.011 0.016 0.014 0.029 0.030 0.029

Sharpening 0.035 0.712 0.374 0.066 0.110 0.088 0.081 0.098 0.089

StirMark 0.106 0.110 0.108 0.015 0.018 0.016 0.024 0.026 0.025

Gaussian filtering 0.054 0.075 0.064 0.006 0.014 0.010 0.006 0.010 0.008

Sharpening 0.213 0.255 0.234 0.009 0.019 0.014 0.015 0.015 0.015

StirMark 0.025 0.029 0.027 0.002 0.003 0.002 0.004 0.004 0.004

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

242

The

entropic power was also estimated on the

n original coefficient vector. The bandwidth W

was computed as half the frame rate.

When considering the capacity value in eq. (A8),

the model provided by the present study (

i.e. the pdf

in Table 1) is considered as the noise

pdf )(np

The

)(xp

function giving the capacity value is

searched for by means of a numerical strategy.

Actually, it is considered that

)(xp

itself can be

represented as a mixture of 5 Gaussian laws, thus

restricting the searching to a space with 15

dimensions (5 weights, 5 means values and 5

variances). These 15 dimensions are not

independent. First, the sum of weights should

equal 1. Secondly, the mean of the mark (

i.e. the

mixture mean) is set to 0 (a generally accepted

assumption in watermarking). Thirdly, the mixture

variance was set so as to ensure a good transparency

(

i.e. 30dB lower than the host video).

The capacity values computed with the general

formula and with Shannon limits are shown in

Table 3. A general agreement between the two types

of capacity estimation can e noticed, with some

exceptions (for

of Gaussian filtering, StirMark).

At the same time, the capacity estimation starting

from the attack models is compulsory when a certain

degree of precision is required: that capacity

evaluation by limits can lead at relative errors of

about 100% and larger!

Table 3: Capacity value and limits (lower and upper ) for

rank

r = 1, r = 150 and r=300.

Rank

Attack

Capacity

Gaussian

filtering

Sharpening StirMark

value 3.567 1.332 2.307

r = 1

limits

(3.632 ;

3.651)

(1.268 ;

1.725)

(2.394 ;

2.415)

value 0.339 0.251 0.259

r =

150

limits

(0.037 ;

0.949)

(0.004 ;

0.569)

(0.005 ;

0.273)

value 0.055 0.006 0.009

r =

300

limits

(0.018 ;

0.935)

(0.002 ;

0.621)

(0.002 ;

0.273)

5 CONCLUSIONS

The present paper brings into evidence that some

real life watermarking attack effects are stationary in

the DCT hierarchy and accurately estimates the

corresponding probability density functions. Then,

these models are involved in capacity evaluation.

From the applicative point of view, beyond

watermarking itself (

i.e. reaching the capacity limit

in a practical application), these results are the

starting point for a large variety of applications in

the multimedia content processing, as smart

indexing or in-band content enrichment, for

instance.

Further work will be also devoted to considering

the Blahut approach for watermarking capacity

evaluation.

ACKNOWLEDGEMENTS

This work is partially supported by the HD3D-IIO

project of the Cap Digital competitiveness cluster.

REFERENCES

Archambeau, C., Lee, J., Verleysen, M., 2003.

Convergence Problems of the EM Algorithm for

Finite Gaussian Mixtures, Proc. 11th European

Symposium on Artificial Neural Networks

, Bruges,

Belgium, pp. 99-106.

Archambeau, C., Verleysen, M., 2003. Fully

Nonparametric Probability Density Function

Estimation with Finite Gaussian Mixture Models,

Proc. ICAPR, Calcutta, India, pp. 81-84.

Archambeau, C., Valle, M., Assenza, A., Verleysen, M.,

2006. Assessment of Probability Density Estimation

Methods: Parzen Window and Finite Gaussian

Mixtures,

Proc. IEEE International Symposium on

Circuits and Systems

, Kos, Greece.

Basseville, M., 1996. Information: entropies, divergences

et moyennes,

Internal report–INRIA, N°1020.

Costa, M., 1983. Writing on dirty paper,

IEEE

Transactions on Information Theory

, Vol. IT-29, pp.

439-441.

Cox, I., Miller, M., Bloom, J., 2002.

Digital

Watermarking

, Morgan Kaufmann Publishers.

Dempster, A.P., Laird, N.M., Rubin, D.B., 1977.

Maximum Likelihood from Incomplete Data via the

EM Algorithm,

Journal of the Royal Statistical

Society, Series B

, Vol. 39, No. 1, pp. 1-38.

Dumitru, O., Duta, S., Mitrea, M., Prêteux, F., 2007.

Gaussian Hypothesis for Video Watermarking

Attacks: Drawbacks and Limitations,

EUROCON

2007

, Warsaw, Poland, pp. 849-855.

Dumitru, O., Mitrea, M., Preteux, F., 2007. Accurate

Watermarking Capacity Evaluation, Proc. SPIE, Vol.

6763, pp. 676303:1-12.

Mitrea, M., Prêteux, F., Petrescu, M., 2006. Very Low

Bitrate Video: A Statistical Analysis in the DCT

Domain, LNCS, Vol. 3893, pp. 99-106.

DCT DOMAIN VIDEO WATERMARKING - Attack Estimation and Capacity Evaluation

243

Mitrea, M., Dumitru, O., Prêteux F, Vlad, A., 2007. Zero

Memory Information Sources Approximating to Video

Watermarking Attacks, LNCS, Vol. 4705, pp. 409-423.

Trailovic, L., Pao, L., 2002, Variance Estimation and

Ranking of Gaussian Mixture Distribution in Target

Tracking Applications,

Proc. of the 41st IEEE Conf.

on Decision and Control

, Las Vegas – Nevada, USA,

pp. 2195-2201.

APPENDIX

A1 Pdf Estimation Tools

Be there ],...,,[

21 N

xxx a set of N experimental

data complying with the

iid model. Suppose that

these data are sampled from a random variable

whose

pdf )(xp

is unknown and should be

estimated. A

)(

xp Gaussian mixture is a linear

combination of Gaussian laws and can approximate

any continuous

)(xp pdf (Archambeau & other,

2003):

∑

xpkPxp

)()()(

(A1)

where

)

)(

exp(

)(

πσ

−

−=

The number of mixtures

is pre-established by

the experimenter and

,),( are 3K

parameters to be estimated by the EM (expectation

maximisation) algorithm (Dempster & other, 1977),

based on a maximum likelihood criterion:

 the E step:

)(

)()(

)(

kPxp

xkp

= ,

(A2)

 the M step:

∑

xkp

xxkp

)(

)1(

)(

∑

⎟

⎠

⎞

⎜

⎝

⎛

−

xkp

xxkp

)(

)1(

)(

)1(2

)(

∑

⋅=

xkp

)()1(

)(

)( ,

(A3)

where the (

i ) upper index denotes the current

iteration; the total number of iterations is also

subject to the experimenters choice.

The relationship among the parameters of the

individual Gaussian laws and the mixture parameters

is given in (Trailovic, Pao, 2002).

Alongside with the similarity measure defined in

eq. (1), two popular methods for

pdf comparison are

involved in the experiments (Basseville, 1996):

 Kullback-Leibler divergence:

xuvuD

∫

)(

log)(),(

;

(A4)

 Hellinger distance:

(

)

∫

−=

dxxvxuvuD

)()(

),( .

(A5)

A2 Capacity Evaluation Basis

The capacity of a continuous channel, whose input

and output information sources are denoted by

and

is given by the Shannon’s formula (A6):

∫∫

),(max

)(

dxdyyxfC

(A6)

)()(

),(

log),(),(

ypxp

yxp

yxpyxf

XYXY

where

)(xp

and )(yp

stand for the input and

output

pdfs, while ),( yxp

is the joint pdf of

and

. The

, xx and

, yy are the limits of the

intervals on which the input and output

pdfs have

non-zero values. In the case of a non-Gaussian

noise, Shannon derives some upper and lower limits,

eq. (A7):

loglog

≤≤

(A7)

where

W is the channel bandwidth,

is the signal

power,

N is the noise power, and

N is the noise

entropy power (

i.e. the power of a white-type noise

which has the same bandwidth and entropy as the

considered noise).

When assuming the noise is additive and

independent, eq. (A6) becomes:

dydxyxgC

∫∫

),(max

)(

(A8)

∫

−

−=

)()(

)(

log)()(),(

NXXY

dnnypnp

xyp

xypxpyxg

where the noise limits are

111

xyn −= and

222

xyn

−

(Dumitru, & others, 2007).

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

244