ROBUST CONTROL OF THE C5 PARALLEL ROBOT
B. Achili
∗+
, B. Daachi
∗
, A. Ali-Cherif
+
and Y. Amirat
∗
+
Laboratoire d’Informatique Avanc´ee de Saint Denis, 2 rue de la libert´e 93526 Saint Denis Cedex, France
∗
Laboratoire Images, Signaux et Syst`emes intelligents, 122-124 rue Paul Armangot, 94400 Vitry/seine, France
Keywords:
Parallel robot, Robust control, Stability analysis.
Abstract:
This paper deals with the dynamic control of a parallel robot with C5 joints. Computed torque control and
robust control have been studied and implemented. For this purpose, we have used the inverse dynamic model
whose parameters have been experimentally identified. The closed loop stability has been studied using the
Lyapunov principle. The addition of a robustness term based on sliding mode technique ensures good tracking
performances. The experimental results show the effectiveness of the robust control.
1 INTRODUCTION
Parallel manipulator is a closed-loop mechanism in
which the end-effector(mobile platform) is connected
to the base by at least two independent kinematic
chains. Compared to the serial ones, the parallel ar-
chitectures have potential advantages in terms of stiff-
ness, accuracy, high speed and payload. They are
widely applied to the following fields, like the Pick
and Place operation in food, medicine, electronic in-
dustry, etc.
Due to their complex architecture, precise and ro-
bust control of parallel machines is a hard and open
problem which has been widely addressed in the lit-
terature. When the task requires fast motion of robot
and high precision, it is very important to design a
controller with good performances in order to match
the mechanism. In literature, various control methods
are proposed such as proportional, integration, deriva-
tive (PID) control, computed torque control (Middle-
ton and Goodwin, 88) adaptive control (Slotine and
Li, 88), neural networks control (Miller et al, 87),
fuzzy control, fuzzy adaptive control.
Computed torque control has been proposed in the
litterature. The latter requires the exact knowledge of
inverse dynamic model. In theory, it ensures the de-
coupling and the linearization of equations of robot
motion, resulting in a uniform response for any robot
configuration . This technique is more efficient in
term of precision for high moving than PD and PID
linear control. However it is sensitive to the parame-
ter variations and external disturbances of the system
(Zhiong et al, 07). In practice, the dynamic model of
robot can not be exactly known. Therefore in order to
circumvent the problem of dynamic model uncertain-
ties, an adaptive technique is needed.
In literature, several works have been published
in the field of intelligent control methods such as
Fuzzy control, neural network control (Miller et al,
87). Thus, a fuzzy neural network hybrid control
(FNN) is proposed. In this control technique the hy-
brid control system, combines the computed torque
controller, the FNN uncertainty observer and a com-
pensated controller to control the position of a slider
of the motor–toggle servomechanism. Recently, a
new approach, combining the computed torque con-
trol with fuzzy control has been proposed in litera-
ture. The latter is used to approximate lumped un-
certainty due to parameters variations. Among other
recent work, an on-line updated PID algorithm is pro-
posed (Chen and Huang, 2004).
In this paper, we have addressed the robust control
of a parallel robot with C5 joints. This type of con-
trol allows us to improve the trajectory tracking for
fast motions. This approach is based on sliding mode
technique. It consist to add a compensation term in
the control law in order to compensate the identifica-
tion and modeling errors.
This paper is organized in five sections. The first
one describes the mechanical architecture of the C5
parallel robot. The second section presents the dy-
namic model and its properties. Section 3 is devoted
to the control law synthesis. Section 4 is dedicated to
the presentation and analysis of the experimental re-
183
Achili B., Daachi B., Ali-Cherif A. and Amirat Y. (2008).
ROBUST CONTROL OF THE C5 PARALLEL ROBOT.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 183-186
DOI: 10.5220/0001499201830186
Copyright
c
 SciTePress

sults. Finally, a conclusion and some perspectives are
given in the last section.
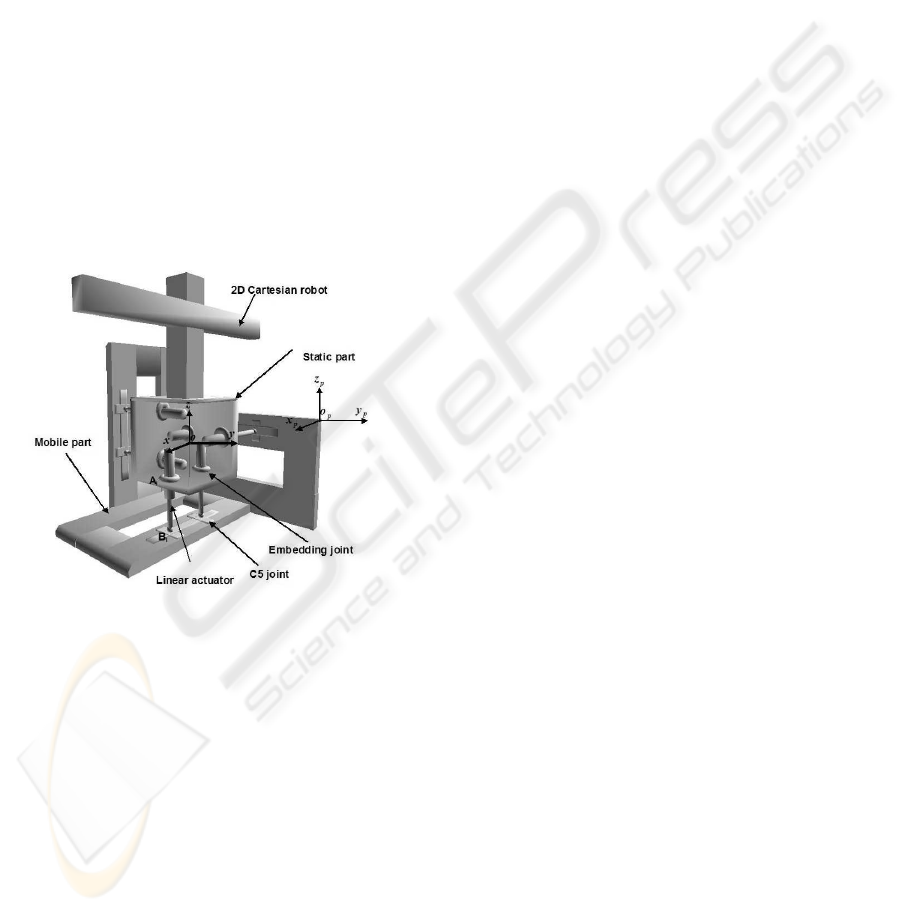
2 DESCRIPTION OF THE C5
PARALLEL ROBOT
The C5 parallel robot consists of a static part and a
mobile part connected together by six actuated links.
Each segment is embedded to the static part at point
A
i
and linked to the mobile part through a spherical
joint attached to two crossed sliding plates at point B
i
(Fig. 1)
Theoretical study concerning this architecture has
been presented in the literature. The C5 links paral-
lel robot is equipped with six linear actuators; each of
them is driven by a DC motor. Each motor drives a
ball and screw arrangement. The position measure-
ments are obtained from six incremental encoders,
which are tied to the DC motors.
Figure 1: Parallel robot.
3 DYNAMIC MODEL AND
PROPERTIES
The dynamic model of the considered parallel robot
is given by the following equation :
Γ = M(q) ¨q+ H(q, ˙q) (1)
with
• q the (6× 1) vector of joint positions
• ˙q the (6× 1) vector of joint velocities
• ¨q the (6× 1) vector of joint accelerations
• M(q) the (6× 6) inertia matrix
• H (q, ˙q) the(6 × 1) vector of gravitational forces,
frictions, Coriolis centripetal forces and other dy-
namics.
• Γ the vector of the torques.
The robot dynamics (1) have physical properties
that can be used in the control law synthesis :
Property 1. The matrix M is Symmetric Positive
Definite (SPD).
Property 2. The matrix C can be chosen so that
˙
M −
2C is skew symmetric.
Matrices M and H are identified by using least
squares method. We note by
ˆ
M and
ˆ
H the estimation
of M and H respectively. The detail of this identifica-
tion method is given in (Janot et al, 07).
4 CONTROL LAW SYNTHESIS
Assuming that the dynamic model is exactly identi-
fied (case of negligible identification errors), we can
use the following control law :
Γ =
ˆ
M(q) ¨q
r
+
ˆ
H(q, ˙q) (2)
with
¨q
r
= ¨q
d
+ k
v
˙e+ k
p
e (3)
e = (q
d
− q) (4)
˙e = ( ˙q
d
− ˙q) (5)
where
• e is the trajectory tracking error vector
• q
d
, ˙q
d
, ¨q
d
are respectively, desired joint positions,
velocities and accelerations
• k
p
and k
v
are respectively, diagonal positive def-
inite matrices that represent the proportional and
derivatives gains.
The combination of equations (2 and (3) gives the
following equation:
¨e+ k
v
˙e+ k
p
e = 0 (6)
The solution of equation (6) is globaly exponen-
tially stable. In our case, the functions of the dy-
namic model (matrices M and H) are estimated by
least squares method. The parameters of these func-
tions are fixed. The robot carries out different tasks
and generally the identification error is never close to
zero. It is then imperative to take into account these
identification errors. For this purpose, we introduce
in the control law a term of robustness δu based on
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
184

the sliding mode technique. The control law is then
given by:
Γ =
ˆ
M(q) ¨q
r
+
ˆ
H(q, ˙q) + δu (7)
In closed loop, the equation of the dynamic error
is given by :
¨e+ k
v
˙e+ k
p
e =
ˆ
M
−1

(M −
ˆ
M) ¨q+ (H −
ˆ
H) − δu

(8)
We consider the state form of the equation (9) :
˙
e = A e+ B
ˆ
M
−1

(M −
ˆ
M) ¨q+ (H −
ˆ
H) − δu

(9)
with
• e =

e
˙e

• A =

0 I
−k
p
−k
v

• B =

0
I

• 0 and I are the(n× n) zero and identity matrix re-
spectively.
Consider a new signal error s:
s = Ce (10)
with
C =

Λ I

(11)
Λ is a positive diagonal matrix, such that the
transfer matrix [C(pI − A)
−1
B] is strictly positive real
(SPR). For the purpose of the stability analysis we
use the formulation given in (Meddah, 98).
We choose δu inspired from sliding-mode theory
as follows :
δu = βsign(s) (12)
where β is the sliding gain.
For stability study, we use the followingLyapunov
function V :
V(t) =
1
2
e
T
Pe (13)
where P is a symmetric positive definite matrix
solution of the Lyapunov equation:
A
T
P+ AP = −Q
PB = C
T
Q a symmetric positive definite matrix.
The time derivative of the Lyapunov function (13)
is expressed by the following equation:
˙
V(t) = −
1
2
e
T
Qe (14)
+s
T
ˆ
M
−1

(M −
ˆ
M) ¨q+ (H −
ˆ
H) − βsign(s)

Consequently
˙
V ≤ 0 when the following inequal-
ity is satisfied :
β ≥
λ
max
ˆ
M
λ
min
ˆ
M


(M −
ˆ
M) ¨q+ (H −
ˆ
H)


(15)
where λ
max
ˆ
M
and λ
min
ˆ
M
are respectively the greatest
eigen value and the smallest eigen value of
ˆ
M
−1
.
If we choose the gain β, according to( 15) we ob-
tain :
˙
V(t) ≤ −
1
2
e
T
Qe
for any t ≥ 0, thus s is bounded.
To prove that s → 0 when t → ∞, we can apply a
Barbalat lemma to the following non negative func-
tion :
V
1
(t) = V(t) −
t
Z
0

˙
V(t) +
1
2
e
T
Qe

dτ (16)
˙
V
1
(t) = −
1
2
e
T
Qe (17)
˙
V
1
(t) is uniformly continuous.
According to Barbalat lemma we can conclude
that
˙
V
1
(t) → 0 and consequently e → 0 and s → 0.
Therefore the system represented by equation (9) is
asymptotically stable.
Even if the value of the gain β is determined from
condition (15), it is difficult to find this value as ma-
trices M and H are unknown. Thus it is not possible
to obtain the exact value of ((M −
ˆ
M) ¨q + (H −
ˆ
H)).
In practice, β is chosen heuristically. Note that the
term sign used in (14) produces the chattering phe-
nomenon in the control input. In order to avoid this
drawback, Slotine and Li (Slotine and Li, 91) propose
to replace the function sign by the function sat. (satu-
ration)
5 EXPERIMENTAL RESULTS
In this section we present the experimental results of
the application of the control laws described in sec-
tion 4. These control approach is compared to a PID
control. A chirp function is used as a desired trajec-
tory, the frequency varies between 0.1hz and 0.3hz.
The trajectory tracking error concerning the first axis
(filtered by the 4th order Butterworth) is shown in Fig.
2. Concerning other axis, we obtained the same per-
formance as the first one.
ROBUST CONTROL OF THE C5 PARALLEL ROBOT
185

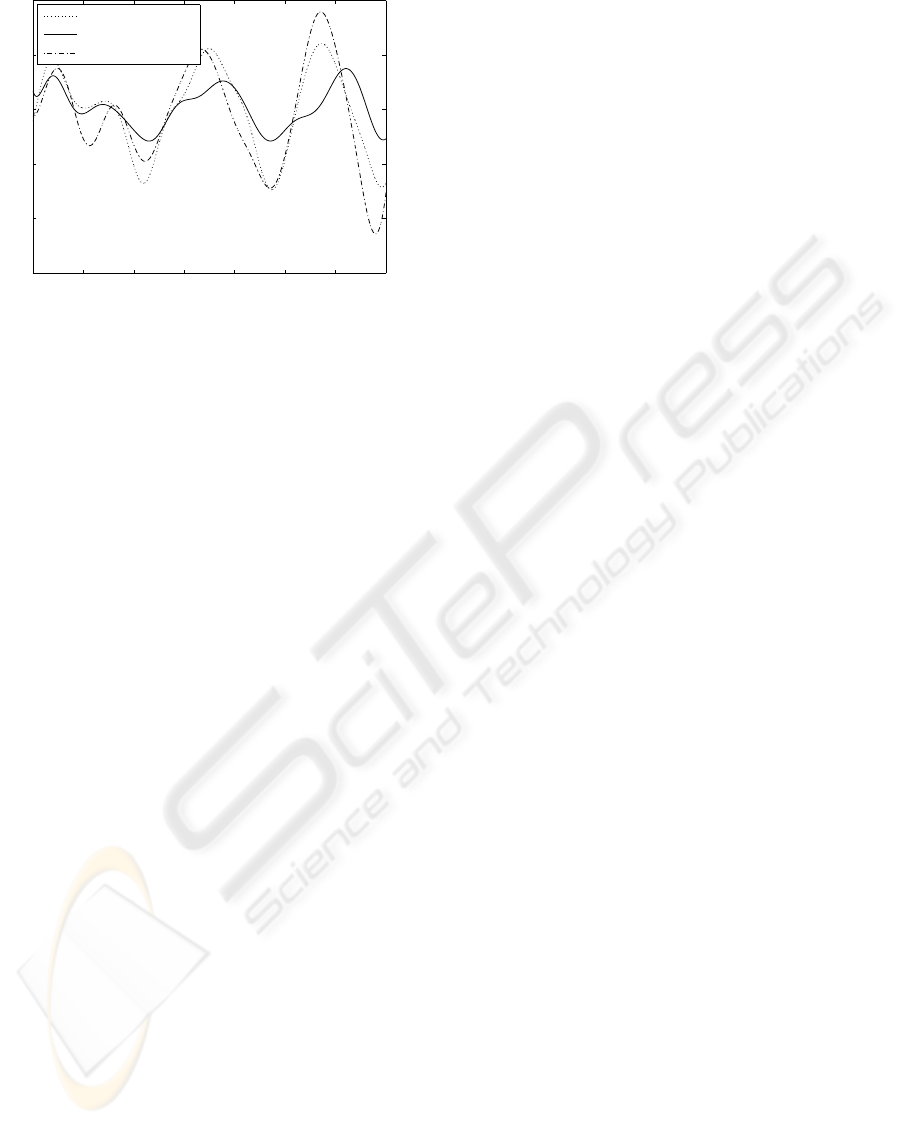
0 1000 2000 3000 4000 5000 6000 7000
−1.5
−1
−0.5
0
0.5
1
x 10
−3
Time [ms]
Tracking error [m]
Joint 1
Computed torque control
Robust control
PID control
Figure 2: Tracking error of computed torque control, robust
control and PID control.
5.1 Discussion
Figure 2 show that computed torque approach clearly
improve the tracking performances compared to the
PID control, but it remains insufficient because the
precise values of M and H are difficult to obtain due to
measuring errors, environment and parameters vari-
ations. Therefore, we can conclude that computed
torque method exhibits good performances only when
robot dynamics model is precisely identified.
However, we obtained good tracking perfor-
mances when the robust control (control law with
compensation term δu) is used. Besides, we also note
that the errors increase for fast motions due to PID
control. For robust control, these errors remain small
with respect to PID control and Computed torque con-
trol errors.
6 CONCLUSIONS
In this paper, we implemented a sliding mode ap-
proach for the robust control of the C5 parallel robot.
The stability of the system in closed loop with the
control law including a compensation term is guar-
anteed. Thereafter a comparative study of above ap-
proaches show that the control using a robust term en-
sures a good trajectory tracking compared to the oth-
ers presented approaches. The experimental results
show clearly that the robustness term, based on the
sliding mode method, reduces the effect of the identi-
fication errors. In our short term project, we propose a
new control law such that the identification and mod-
eling errors will be compensated in an adaptive way.
REFERENCES
Zhiyong Y., Jiang W., Jiangping M., 2007. Motor-mecanism
dynamic model based neural network optimized com-
puted torque control of a high speed parallel manipu-
lator, Mechatronics 17 381-390.
Song Z., Yi J., Zhao D., Li X., 2005. A computed torque
controller for uncertain robotic manipulator system:
Fuzzy approach, Fuzzy Sets and Systems 154 208-
226.
Chen J., Huang T.C., 2004 Applying neural networks to
on-line updated PID controllers for nonlinear process
control, J Process Control; 14:211–30.
Middleton R.H., Goodwin G.C., 1988. Adaptive computed
torque control for rigid link manipulators, System
Control Lett. 10 9–16.
Slotine J.J.E., Li W., 1988. Adaptive manipulator control:
a case study, IEEE Trans. Automat. Control 33 995–
1003.
Janot A., Bidard C., Gosselin F., Gautier M., Keller D., Per-
rot Y., 2007, Modelingand Identifi cation of a 3 DOF
Haptic Interface,IEEE International Conference on
Robotics and Automation Roma, Italy, 10-14 pp4949-
4955.
Meddah Y. D., 1998. Identification et commande neu-
ronales de syst`emes non lin´eaires : Application aux
syst`emes Robotis´es. Th`ese de doctorat de l’universit´e
Pierre et Marie Curie.
Miller W.T., Glanz F.H., Kraft L.G., 1987, Application of
a general learning algorithm to the control of robotic
manipulators, Int. J. Robot. Res. 6 84–98.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
186