A NOVEL PARTICLE SWARM OPTIMIZATION APPROACH FOR
MULTIOBJECTIVE FLEXIBLE JOB SHOP SCHEDULING
PROBLEM
Souad Mekni, Besma Fayech Char and Mekki Ksouri
ACS, Ecole Nationale d.Ingnieurs de Tunis, Tunisia
Keywords:
Flexible Job Shop Scheduling, Multiobjective Optimization, Particle Swarm Optimization, Smallest Position
Value.
Abstract:
Because of the intractable nature of the .exible job shop scheduling problem and its importance in both .elds
of production management and combinatorial optimization, it is desirable to employ e cient metaheuristics in
order to obtain a better solution quality for the problem. In this paper, a novel approach based on the vector
evaluated particle swarm optimization and the weighted average ranking is presented to solve .exible job shop
scheduling problem (FJSP) with three objectives (i) minimize the makespan, (ii) minimize the total workload
of machines and (iii) minimize the workload of critical machine. To convert the continuous position values to
the discrete job sequences, we used the heuristic rule the Smallest Position Value (SPV). Experimental results
in this work are very encouraging since that relevent solutions were provided in a reasonable computational
time.
1 INTRODUCTION
Solving a NP-hard scheduling problem with only one
objective is a difficult task. Adding more objectives
obviously makes this problem more difficult to solve.
In fact, while in single objective optimization the op-
timal solution is usually clearly defined, this does not
hold for multiobjective optimization problems. In-
stead of a single optimum, there is rather a set of good
compromises solutions, generally known as Pareto
optimal solutions from which the decision maker will
select one. These solutions are optimal in the wider
sense that no other solution in the search space is su-
perior when all objectives are considered. Recently,
it was recognized that Particle Swarm Optimization
(PSO) was well suited to multiobjective optimization
mainly because of its fast convergence.
The Particle Swarm Optimization (PSO) is a pop-
ulation based search algorithm developed by Kennedy
and Eberhart in 1995 (Kennedy, 1995) (Abraham,
2006, pp. 3-15) (Clerc, 2005) inspired by social be-
haviour of bird flocking or fish schooling. Unlike Ge-
netic Algorithms (GA), PSO has no evolution oper-
ators such as crossover and mutation. In PSO, the
population is initialized randomly and the potential
solutions, called particles (Hu, 2004) fly through the
search space with velocities which are dynamically
adjusted according to their historical behaviors. In
PSO, each particle is influenced by both the best solu-
tion that it has discovered so far and the best particle
in its neighbors (local variant of PSO) or in the entire
population (global variant of PSO).
Figure 1 shows the general flow chart of PSO. At
each time step, the behaviour of a given particle is a
compromise between three possible choices:
- to follow its own way
- to go towards its best previous position
- to go towards the best neighbour
This compromise is formalized by equations (1)
and (2) and illustrated by figure 2.
v
→
i
(t + 1) = c
1
∗ v
→
i
(t) + c
2
∗ (p
→
i
(t) − x
→
i
(t))1 (1)
+c
3
∗ (p
→
g
(t) − x
→
i
(t)) (2)
x
→
i
(t + 1) = x
→
i
(t) + v
→
i
(t + 1) (3)
225
Mekni S., Fayech Char B. and Ksouri M. (2008).
A NOVEL PARTICLE SWARM OPTIMIZATION APPROACH FOR MULTIOBJECTIVE FLEXIBLE JOB SHOP SCHEDULING PROBLEM.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 225-230
DOI: 10.5220/0001499402250230
Copyright
c
 SciTePress

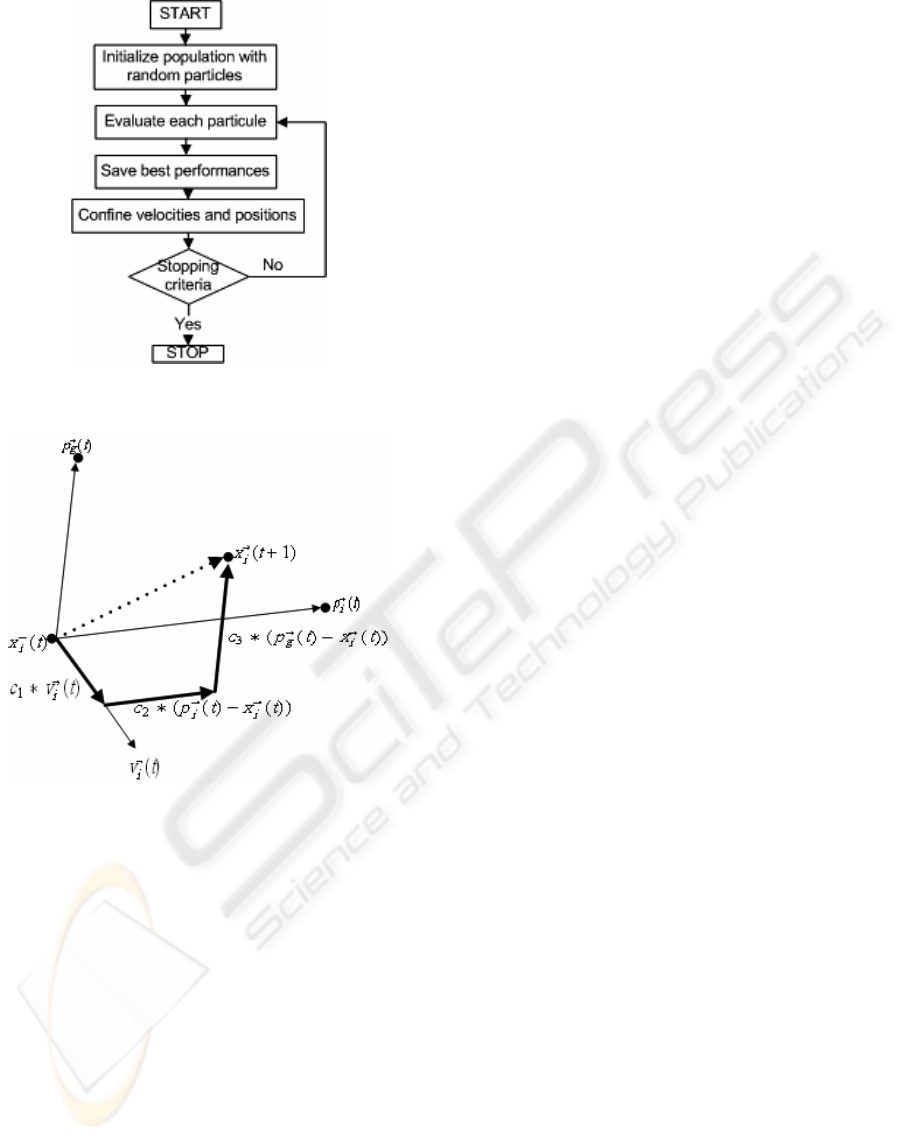
Figure 1: The mapping between particle and FJSP.
Figure 2: An illustration of particle’s move.
with
• v
→
i
(t): velocity of particle i at iteration t
• p
→
i
(t): best previous position of particle i at itera-
tion t
• p
→
g
(t): best neighbour of particle i at iteration t
• x
→
i
(t): position of particle i at iteration t
• c
1
,c
2
,c
3
: positive random numbers. These num-
bers are social-confidents coefficients
Although PSO is still new in evolutionary com-
putation field, it has been applied to a plethora of
problems in science and engineering. Multiobjec-
tive optimization problem (MOO) has been one of
the most studied application areas of PSO algorithms
(Coello, 2002), (Coello, 2004), (Hu, 2002), (Par-
sopoulos, 2002), (Hu, 2003). Number of approaches
have been used and/or designed to manage MOO
problems using PSO. A straight forward approach is
to convert MOO to a single objective optimization
problem. One simple implementation of the conver-
sion is the so-called weighted aggregation approach
which sums all the objectives to form a weighted com-
bination (Shi, 2004) (Mendes, 2004). Weights can be
either fixed or adapted dynamically during the opti-
mization.
Other approaches combine Pareto dominance with
PSO in order to identify Pareto fronts. Most of the re-
search studies developed in this field used two dimen-
sional objectives. It may seem that using only two ob-
jectives oversimplifies the problem (Mendes, 2004).
In this paper, an application of the particle swarm op-
timization algorithm to the flexible job shop schedul-
ing with three objectives is reported. The main goal
of our research is to design mecanisms to extend PSO
such that it can generate solutions of ”good quality”
either for the individual optimization of criteria or for
the compromise between the different objectives.
2 MATHEMATICAL
FORMULATION
The flexible job shop scheduling problem was studied
in (Chetouane, 1995), (Mesghouni, 1999), (Kacem,
2002), (Dupas, 2004), (Xia, 2005), (Abraham, 2006),
(Liu, 2006), (Liu, 2007). FJSP belongs to the NP-
hard family (Sakarovitch, 1984). It presents two dif-
ficulties. The first one is the assignment of each oper-
ation to a machine, and the second is the scheduling
of this set of operations in order to optimize our cri-
teria. The result of a scheduling algorithm must be
a schedule that con-
tains a start time and a resource assignment to each
operation.
The data, constraints and objectives of our prob-
lem are as follows:
2.1 Data
• M represents a set of m machines. A machine is
called M
k
(k = 1,...,m), each M
k
has a load called
W
k
.
• N represents a set of n jobs. A job is called J
i
(i = 1,...,n), each job has a linear sequence of n
i
operations.
• O
i, j
represents the operation number j of the job
number i. The realization of each operation
O
i, j
requires a machine M
k
and a processing time
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
226

p
i, j,k
. The starting time of O
i, j
is t
i, j
and the end-
ing time is t
f
i, j
.
2.2 Constraints
• Machines are independent of one another.
• Each machine can perform operations one after an-
other.
• Each machine is available during the scheduling.
• A started operation runs to completion.
• Jobs are independent of each another.
In our work, we suppose that:
- Machines are available since the date t = 0.
- Each job j
i
can start at the date t = 0.
- The total number of operations to perform is
greater than the number of machines.
2.3 Criteria
We have to minimize Cr1, Cr2 and Cr3:
• The makespan:
Cr1 = max
1≤i≤n
( max
1≤ j≤n
i
(t
f
i, j
))
• The total workload of machines:
Cr2 =
∑
1≤k≤m
(W
k
)
• The workload of the most loaded machine:
Cr3 = max
1≤k≤m
(W
k
)
These criteria are often conflicting. In fact, bal-
ance resource usage by minimizing the utilization of
bottleneck equipement can be antagonistic with the
minimization of the total time of production.
2.4 Lower Bounds
Lower bounds are usually used to measure the qual-
ity of solutions found. For our work, we use lower
bounds proposed in (Dupas, 2004):
• BCr1: (lower bound for Cr1)
BCr1 = max
i
(
∑
j
min
k
(p
i, j,k
))
• BCr2: (lower bound for Cr2)
BCr2 =
∑
i, j
min
k
(p
i, j,k
)
• BCr3: (lower bound for Cr3)
BCr3 = dBCr2/me
3 PSO FOR FJSP
3.1 Particle Representation and Initial
Swarm Generation
One of the key issues when designing the PSO algo-
rithm lies on its solution representation which directly
affects its feasibility and performance. In this paper,
an operation-based representation is used. For the (m
machines, n jobs, O operations) FJSP, each particle
contains O number of dimensions corresponding to
O operations and has a continuous set of values for
its dimensions which represents particle’s positions.
The Smallest Position Value (Tasgetiren, 2004) (Tas-
getiren, 2006), the SPV rule is used to find the permu-
tation of operations and a randomly generated number
is used to find the machine to which a task is assigned
to during the course of PSO. Figure 3 illustrates the
solution representation of a particle corresponding to
FJSP described in table 1 and table 2. The smallest
component of the particle’s position is −2,25 which
corresponds to the operation number 6 of job number
2. Thus, job 2 is scheduled first. The second smallest
component of the particle’s position is −0,99 which
corresponds to the operation number 2 of job number
1. Therefore, job 1 is the second job in the ordering,
etc.
Table 1: Processing time of operations of a (3 Jobs, 5 Ma-
chines) problem.
M
1
M
2
M
3
M
4
M
5
O
1,1
1 9 3 7 5
O
1,2
3 5 2 6 4
O
1,3
6 7 1 4 3
O
2,1
1 4 5 3 8
O
2,2
2 8 4 9 3
O
2,3
9 5 1 2 4
O
3,1
1 8 9 3 2
O
3,2
5 9 2 4 3
Table 2: The operating sequences of jobs of a (3 Jobs, 5
Machines) problem.
J
1
O
1,1
O
1,2
O
1,3
J
2
O
2,1
O
2,2
O
2,3
J
3
O
3,1
O
3,2
The PSO randomly generates an initial swarm of
S particles, where S is the swarm size. These particle
vectors will be iteratively updated based on collective
experiences in order to enhance their solution quality.
A NOVEL PARTICLE SWARM OPTIMIZATION APPROACH FOR MULTIOBJECTIVE FLEXIBLE JOB SHOP
SCHEDULING PROBLEM
227

Figure 3: The mapping between particle and FJSP.
3.2 Our Approach
Our approach is a novel proposal to solve multiobjec-
tive optimization problems using PSO. It is inspired
by The Vector Evaluated Particle Swarm Optimiza-
tion (VEPSO)(Parsopoulos, 2002b) algorithm wich
incorporates ideas from the Vector Evaluated Genetic
Algorithm (VEGA) (Shaffer, 1985).
Our approach is based on the use of Weighted Av-
erage Ranking (WAR) (Collette, 2002) and a subdi-
vision of decision variable space into (k + 1) sub-
swarms (k: is the number of criteria). Each sub-
swarm i (i between 1 and k) is exclusively evaluated
with the objective function number i, but, information
coming from other sub-swarm(s) especially from the
sub-swarm number (k +1) is used to influence its mo-
tion in the search space. The execution of the flight of
each sub-swarm can be seen as an entire PSO process
(with the difference that it will optimize only a part
of the search space and not the entire search space).
The sub-swarm (k +1) looks for the solutions of com-
promise between the k studied criteria. It generates
the leaders set among the particle swarm set by us-
ing the Weighted Average Ranking. Leaders of other
sub-swarms can migrate to the sub-swarm (k + 1) un-
til a number of iterations is reached in order to variate
the selection pressure. The procedure of exchanging
information among sub-swarms can lead to Pareto op-
timal points.
Stages of the algorithm described in figure 1 are
repeated until a certain prefixed number of iterations
is reached.
4 PERFORMANCE MEASURES
Different instances of the present problem have been
chosen to test our approach, in order to ensure a cer-
tain diversity. These instances present a number of
operations between 8 and 56 (the number of jobs is
between 3 and 15) and a number of resources be-
tween 4 and 10 machines. The studied problem na-
ture is varied enough according to the performance
of resources, their flexibility and the number of the
precedence constraints. So, cases of parallel machine
problems, where all the machines have the same per-
formance, have been also tested. We also studied total
and partial flexibility cases when machines presented
variable performances. As results to the simulations,
some findings can be pulled:
• Most particular problems have been solved in an
optimal manner (case of problems having parallel
machines).
• The problems with parallel machines are easier to
solve than the problems having machines with
variable performance.
• The found solutions are generally of a good qual-
ity. Is is noted while comparing them with the ex-
isting approaches in the literature and also while
comparing obtained values of the criteria with the
computed lower bounds. As an illustration, we
choose to present the following instance: we con-
sider the problem described in table 3 (10 jobs,
30 operations, 10 machines). The computation
of the different lower bounds gives the follow-
ing values: BCr1 = 7, BCr2 = 41, BCr3 = 4.
This example has been already processed in the
literature by many methods: temporal decom-
position (Chetouane, 1995), classic GAs (Mes-
ghouni, 1999), approach by localization and ap-
proach by localization and controlled EAs and ap-
proach by hybridizating particle swarm optimiza-
tion and simulated annealing (Xia, 2005). The
schedule obtained in these cases is characterized
by the following values presented in figure 4.
Figure 4: Solutions in the literature of (10J, 10M).
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
228

Table 3: Matrix of processing times of FJSP (10J,10M).
5 CONCLUSIONS
This paper presents a novel approach using parti- cle
swarm optimization to solve the multicriteria .exible
job shop scheduling with total or partial .exibility. It
is based on the vector evaluated particle swarm opti-
mization and the weighted av- erage ranking.
Our work, resulted in to the development of a
generic method to resolve multiobjective opti- miza-
tion. It provides relevant solutions for the individ-
ual optimization of criteria or for the com- promise
between the dierent objectives. Future research will
cover an investigation on the eects of diversity control
in the search performances of multiobjective particle
swarm optimization.
REFERENCES
Abraham A., Guo. H, Liu. H., Swarm Intelligence: Founda-
tions, Perspectives and Applications. Studies in Com-
putational Intelligence (SCI) 26;pp. 3-25; 2006.
Abraham A., Lui H. and Ghang T. G., Variable neigh-
borhood Particle Swarm Optimization Algorithm. In
GECCO’06 Seattle, Washington, USA, July 8-12,
2006.
Chetouane F., Ordonnancement d’atelier tches gnralises,
perturbations, ractivit. Rapport DEA de l’institut na-
tional polytechnique de Grenoble, 1995.
Clerc. M., L’optimisation par essaims particulaires, ver-
sions paramtriques et adaptatives. Edition Herms,
Lavoisier, 2005.
Collette Y., Siarry P., Optimisation Multiobjectif. Edition
Eyrolles, Paris, 2002.
Coello C. A., Lechuga M. S., MOPSO:A Proposal for Mul-
tiple Objective Particle Swarm Optimization. IEEE
Congress on Evolutionary Computation, Honolulu,
Hawaii USA, 2002.
Coello C. A., Pulido G. T., Lechuga M. S., Handling
Multiple Objectives with Particle Swarm Optimiza-
tion. IEEE Transactions on Evolutionary Computa-
tion, IEEE, Piscataway, NJ, 8(3) 256-279, 2004.
Dupas R., Amlioration de Performance des Systmes de
Production: Apport des Algorithmes volutionnistes
aux Problmes d’Ordonnancement Cycliques et flexi-
bles. Habilitation Diriger des Recherches, Universit
d’Artois, 2004.
Hu X., Shi Y., Eberhart R. C., Recent advances in Particle
Swarm. In Proceedings of Congress on Evolutionary
Computation (CEC), Portland, Oregon, 90-97, 2004.
Hu X., Eberhart R. C., Multiobjective Optimization using
Dynamic Neighborhood Particle Swarm Optimiza-
tion. Proceeding of the 2002 Congress on Evolu-
tionary Computation, Honolulu, Hawaii, May 12-17,
2002.
Hu X., Shi Y., Eberhart R.C., Particle Swarm with extended
Memory for Multiobjective Optimization. Proc. of
2003 IEEE Swarm Intelligence Symposium, pp 193-
197. Indanapolis, Indiana, USA, IEEE Service Center,
April 2003.
Kacem I., Hammadi S., Borne P., Approach by Localiza-
tion and Multiobjective Evolutionary Optimization for
flexible Job Shop Scheduling Problems. IEEE Trans-
actions on Systems, man and cybernetics-Part c/ Ap-
plications and reviews vol 32, N.1 February , 2002.
Kacem I., Hammadi S., Borne P., Pareto-optimality Ap-
proach for Flexible job-shop Scheduling Problems:
hybridization of evolutionary algorithms and fuzzy
logic. IEEE Transactions on Systems, man and
cybernetics-Part c/ Applications and reviews vol 32,
N.1 February , 2002.
Kennedy J., Eberhart R. C., Particle Swarm Optimiza-
tion. IEEE International Conference on Neural Net-
works(Perth, Australia). IEEE Service Center, Piscat-
away, NJ, IV, pp. 1942-1948; 1995.
Liu H., Abraham A., Choi O., Moon S. H., Vari-
able Neighborhood Particle Swarm Optimization for
Multi-objective Flexible Job-shop Scheduling Prob-
lems. SEAL 2006, 197-204, 2006.
A NOVEL PARTICLE SWARM OPTIMIZATION APPROACH FOR MULTIOBJECTIVE FLEXIBLE JOB SHOP
SCHEDULING PROBLEM
229

Liu H., Abraham A., Grosan C., Li N., A novel Vari-
able Neighborhood Particle Swarm Optimization for
Multi-objective Flexible Job-shop Scheduling Prob-
lems. ICDIM.07 Lyon, France, October 28-31, 2007.
Mendes R., Population Topologies and their Influence in
Particle Swarm Performance. Thse, 2004.
Mesghouni K., Application des Algorithmes volutionnistes
dans les Problmes d’Optimisation en Ordonnance-
ment de la Production. Thse, Universit des Sciences
et Technologies de Lille; 1999.
Parsopoulos, K. E., Verhatis, M. N., Recent Approaches
to Global Optimization Problems through Particle
Swarm Optimization. Natural Computing 1: 235-306,
2002.
Parsopoulos, K. E., Verhatis, M. N.(2002b), Particle
Swarm Optimization Method in Multiobjective Prob-
lems. Proceedings of the 2002 ACM Symposium on
Applied Computing (SAC 2002), pp. 603-607, 2002.
Sakarovitch M., Optimisation Combinatoire. Mthodes
Mathmatiques et Algorithmiques. Hermann, Editeurs
des sciences et des arts, Paris, 1984.
Shaffer D., Multiple Objective Optimization with Vector
Evaluated Genetic Algorithm. In genetic Algorithm
and their Applications: Proceedings of the First In-
ternational Conference on Genetic Algorithm, pages
93-100, 1985.
Shi Y., Particle Swarm Optimization. IEEE Neural
Networks Society, February 2004. PSO Tutorial,
http://www.swarmintelligence.org/tutorials.php
Tasgetiren M. F., Sevkli M., Liang Y. C., Gencyilmaz
G., Particle Swarm Optimization Algorithm for sin-
gle Machine Total Tardiness Problem. IEEE 2004.
Tasgetiren M. F., Sevkli M., Liang Y. C., Yenisey M. M.,
Particle Swarm Optimization and Diferential Evolu-
tion Algorithms for Job Shop Scheduling Problem.
International Journal of Operational Research, vol.3,
N.2, Oct 2006 pp.120-135.
Xia W., Wu Z., An effective Hybrid Optimization Approach
for Multi-objective flexible Job-shop Scheduling Prob-
lems. Computers and Industrial Engineering, 48:409-
425, 2005.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
230