LOCALIZATION OF A MOBILE ROBOT BASED IN ODOMETRY
A
ND NATURAL LANDMARKS USING EXTENDED KALMAN
FILTER
Andre M. Santana, Anderson A. S. Sousa, Ricardo S. Britto, Pablo J. Alsina
and Adelardo A. D. Medeiros
Federal University of Rio Grande do Norte, Natal-RN, Brazil
Keywords:
Robot Localization, Kalman Filter, Sensor Fusion.
Abstract:
This work proposes a localization system for mobile robots using the Extended Kalman Filter. The robot
navigates in an known environment where the lines of the floor are used as natural landmarks and identifiqued
by using the Hough transform.The prediction phase of the Kalman Filter is implemented using the odometry
model of the robot. The update phase directly uses the parameters of the lines detected by the Hough algorithm
to correct the robot’s pose.
1 INTRODUCTION
Borenstein et al. have classified the localization
methods in two great categories: relative localization
methods, which give the robot’s pose relative to the
initial one, and absolute localization methods, which
indicate the global pose of the robot and do not need
previously calculated poses (Borenstein et al., 1997).
As what concerns wheel robots, it is common the
use of encoders linked to wheel rotation axes, a tech-
nique which is known as odometry (Borenstein et al.,
1997). However, the basic idea of odometry is the in-
tegration of the mobile information in a determined
period of time, what leads to the accumulation of er-
rors (Park et al., 1998).
The techniques of absolute localization use land-
marks to locate the robot. These landmarks can be
artificial ones, when introduced in the environment
aiming at assisting at the localization of the robot, or
natural ones, when they can be found in the proper en-
vironment. It is important to underline that even the
techniques of absolute localization are inaccurate due
to noises produced by the manipulated sensors.
Literature shows works using distance measures
to natural landmarks (walls, for example) to locate the
robot. The obtaining of these measures is generally
made with the help of sonar, laser and computational
vision (Lizzaralde et al., 2003; Kim and Kim, 2004;
Pres et al., 1999).
Bezerra used in his work the lines of the
floor composing the environment as natural land-
marks (Bezerra, 2004). Kiriy and Buehler, have used
extended Kalman Filter to follow a number of artifi-
cial landmarks placed in a non-structured way (Kiriy
and Buehler, 2002). Launay et al. employed ceiling
lamps of a corridor to locate the robot (Launay et al.,
2002).
This paper proposes a system enabling to locate
a mobile robot in an environment in which the lines
of the floor form a bi-dimensional grid. To turn it
possible, the lines are identified as natural landmarks
and its characteristics, as well as the odometry model
of the robot, are incorporated in a Kalman Filter in
order to get its pose.
2 THE KALMAN FILTER
The modeling of the Discrete Kalman Filter - DKF
presupposes that the system is linear and described
by the model of the equations of the system (1):

s
t
= A
t
s
t−1
+ B
t
u
t−1
+ γ
t
z
t
= C
t
s
t
+ δ
t
(1)
in which s ∈ R
n
is the vector of the states; u∈ R
l
is the
vector of the control entrances; z ∈ R
m
is the vector of
measurements; the matrix n × n, A, is the transition
187
M. Santana A., A. S. Sousa A., S. Britto R., J. Alsina P. and A. D. Medeiros A. (2008).
LOCALIZATION OF A MOBILE ROBOT BASED IN ODOMETRY AND NATURAL LANDMARKS USING EXTENDED KALMAN FILTER.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 187-193
DOI: 10.5220/0001499601870193
Copyright
c
 SciTePress

matrix of the states; B, n× l, is the coefficient matrix
on entry; matrix C, m × n, is the observation matrix;
γ ∈ R
n
represents the vector of the noises to the pro-
cess and δ ∈ R
m
the vector of measurement errors.
Indexes t and t − 1 represent the present and the pre-
vious instants of time.
The Filter operates in prediction-actualization
mode, taking into account the statistical proprieties
of noise. An internal model of the system is used to
updating, while a retro-alimentation scheme accom-
plishes the measurements. The phases of prediction
and actualization to DKF can be described by the sys-
tems (2) and (3) respectively.
(
¯µ
t
= A
t
µ
t−1
+ B
t
u
t−1
¯
Σ
t
= A
t
Σ
t−1
A
T
t
+ R
t
(2)





K
t
=
¯
Σ
t
C
T
t
(C
t
¯
Σ
t
C
T
t
+ Q
t
)
−1
µ
t
= ¯µ
t
+ K
t
(z
t
− C
t
¯µ
t
)
Σ
t
= (I− K
t
C
t
)
¯
Σ
t
(3)
The Kalman Filter represents the vector of the
states s
t
by its mean µ
t
and co-variance Σ
t
. Matrixes
R, n × n, and Q, l × l, are the matrixes of the co-
variance of the noises of the process (γ) and measure-
ment (δ) respectively, and matrix K, n× m, represents
the prot of the system.
A derivation of the Kalman Filter applied to non-
linear systems is the Extended Kalman Filter - EKF.
The idea of the EKF is to linearize the functions
around the current estimation using the partial deriva-
tives of the process and of the measuring functions
to calculate the estimations, even in the face of non-
linear relations. The model of the system to EKF is
given by the system (4):

s
t
= g(u
t−1
,s
t−1
) + γ
t
z
t
= h(s
t
) + δ
t
(4)
in which g(u
t−1
,s
t−1
) is a non-linear function repre-
senting the model of the system, and h(s
t
) is a non-
linear function representingthe model of the measure-
ments.
Their prediction and actualization phases can be
obtained by the systems of equations (5) and (6) re-
spectively.
(
¯µ
t
= g(u
t−1
,µ
t−1
)
¯
Σ
t
= G
t
Σ
t−1
G
T
t
+ R
t
(5)





K
t
=
¯
Σ
t
H
T
t
(H
t
¯
Σ
t
H
T
t
+ Q
t
)
−1
µ
t
= ¯µ
t
+ K
t
(z
t
− h(¯µ
t
))
Σ
t
= (I− K
t
H
t
)
¯
Σ
t
(6)
The matrix G, n×n, is the jacobian term linearizes
the model and H, l × n is the jacobian term linearizes
the measuring vector. Such matrixes are defined by
the equations (7) e (8).
G
t
=
∂g(u
t−1
,s
t−1
)
∂s
t−1
(7)
H
t
=
∂h(s
t
)
∂s
t
(8)
Next we will describe the modeling of the prob-
lem, as well as the definition of the matrixes which
will be employed in the Kalman Filter.
3 MODELING
3.1 Prediction Phase: Odometer Model
of the Robots Movement
A classic method used to calculate the pose of a robot
is the odometry. This method uses sensors, optical
encoders, for example, which measure the rotation of
the robot’s wheels. Using the cinematic model of the
robot, its pose is calculated by means of the integra-
tion of its movements from a referential axis.
As encoders are sensors, normally their reading
would be implemented in the actualization phase of
the Kalman Filter, not in the prediction phase. Thrun
et al. propose that odometer information does not
function as sensorial measurements; rather they sug-
gest incorporating them to the robot’s model (Thrun
et al., 2005).
In order that this proposal is implemented, one
must use a robot’s cinematic model considering the
angular displacements of the wheels as signal that
the system is entering in the prediction phase of the
Kalman Filter.
Consider a robot with diferential drive in which
the control signals applied and its actuators are not
tension, instead angular displacement, according to
Figure 1.
D
q
d
D
q
d
D
L
D
q
b
D
q
e
r
e
r
d
Figure 1: Variables of the geometric model.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
188

With this idea, and supposing that speeds are con-
stant in the sampling period, one can determine the
geometric model of the robot’s movement(system 9).





















x
t
=x
t−1
+
∆L
∆θ
[sin(θ
t−1
+ ∆θ) − sin(θ
t−1
)]
y
t
=y
t−1
−
∆L
∆θ
[cos(θ
t−1
+ ∆θ) − cos(θ
t−1
)]
θ
t
=θ
t−1
+ ∆θ
(9)
The turn easier the readability of the system (9)
representing the odometry model of the robot, two
auxiliary variables have been employed ∆L and ∆θ

∆L = (∆θ
d
r
d
+ ∆θ
e
r
e
)/2
∆θ = (∆θ
d
r
d
− ∆θ
e
r
e
)/b
(10)
in which ∆θ
d
is the reading of the right encoder and
functions relatively the robot by means of the angular
displacement of the right wheel; ∆θ
e
is the reading of
the left encoder and functions as a displacement ap-
plied to the left wheel; b represents the distance from
wheel to wheel of the robot; r
d
and r
e
are the spokes
of the right and the left wheels respectively.
It is important to emphasize that in real applica-
tions the angular displacement effectively realized by
the right wheel differs of that measured by the en-
coder. Besides that, the supposition that the speeds
are constant in the sampling period, which has been
used to obtain the model 9, is not always true. Hence,
there are differences between the ” angular displace-
ments of the wheels (∆
ˆ
θ
d
e ∆
ˆ
θ
e
) and those ones mea-
sured by the encoders (∆θ
d
e ∆θ
e
). This difference
will be modeled by a Gaussian noise, according to
system (11).
(
∆
ˆ
θ
d
= ∆θ
d
+ ε
d
∆
ˆ
θ
e
= ∆θ
e
+ ε
e
(11)
It is known that odometry possesses accumulative
error. Therefore, the noises ε
d
and ε
e
do not possess
constant variance. It is presumed that these noises
present a proportional standard deviation to the mod-
ule of the measured displacement.
With these new considerations, system (9) is now
represented by system (12):























x
t
=x
t−1
+
∆
ˆ
L
∆
ˆ
θ
[sin(θ
t−1
+ ∆
ˆ
θ) − sin(θ
t−1
)]
y
t
=y
t−1
−
∆
ˆ
L
∆
ˆ
θ
[cos(θ
t−1
+ ∆
ˆ
θ) − cos(θ
t−1
)]
θ
t
=θ
t−1
+ ∆
ˆ
θ
(12)
in which
(
∆
ˆ
L = (∆
ˆ
θ
d
r
d
+ ∆
ˆ
θ
e
r
e
)/2
∆
ˆ
θ = (∆
ˆ
θ
d
r
d
− ∆
ˆ
θ
e
r
e
)/b
(13)
One should observe that this model can not be
used when ∆
ˆ
θ = 0. When it occurs, one uses an
odometry module simpler than a robot (system 14),
obtained from the limit of system 12 when ∆
ˆ
θ → 0.





x
t
= x
t−1
+ ∆
ˆ
Lcos(θ
t−1
)
y
t
= y
t−1
+ ∆
ˆ
Lsin(θ
t−1
)
θ
t
= θ
t−1
(14)
Thrun’s idea implies a difference as what concerns
system (4), because the noise is not audible; rather,
it is incorporated to the function which describes the
model, as system (15) shows:

s
t
= p(u
t−1
,s
t−1
,ε
t
)
z
t
= h(s
t
) + δ
t
(15)
in which ε
t
= [ε
d
ε
e
]
T
is the noise vector connected to
odometry.
It is necessary, however, to bring about a change
in the prediction phase of the system (6) resulting in
the system (16) equations:
(
¯µ
t
= µ
t−1
+ p(u
t−1
,µ
t−1
,0)
¯
Σ
t
= G
t
Σ
t−1
G
T
t
+ V
t
M
t
V
T
t
(16)
in which M, l × l, is the co-variance matrix of the
noise sensors (ε) and V, n × m, is the jacobian map-
ping the sensor noise to the space of state. Matrix V
is defined by the equation (17).
V
t
=
∂p(u
t−1
,s
t−1
,0)
∂u
t−1
(17)
Making use of the odometry model of the robot
described in this section and the definitions of the
matrixes used by the Kalman Filter, we have:
LOCALIZATION OF A MOBILE ROBOT BASED IN ODOMETRY AND NATURAL LANDMARKS USING
EXTENDED KALMAN FILTER
189

G =


1 0 g
13
0 1 g
23
0 0 1


, onde (18)
(19)
g
13
=
∆
ˆ
L
∆
ˆ
θ
[cos(θ
t−1
+ ∆
ˆ
θ) − cos(θ
t−1
)]
g
23
=
∆
ˆ
L
∆
ˆ
θ
[sin(θ
t−1
+ ∆
ˆ
θ) − sin(θ
t−1
)]
V =


v
11
v
12
v
21
v
22
r
d
/b −r
e
/b


, onde (20)
(21)
v
11
= k1cos(k2) − k3[sin(k2) − sin(θ
t−1
)]
v
12
= −k1cos(k2) + k3[sin(k2) − sin(θ
t−1
)]
v
21
= k1sin(k2) − k3[− cos(k2) + cos(θ
t−1
)]
v
22
= −k1sin(k2) + k3[−cos(k2) + cos(θ
t−1
)]
M =

(α
1
|∆
ˆ
θ
d
|)
2
0
0 (α
2
|∆
ˆ
θ
e
|)
2

(22)
Elements m
11
and m
22
in the equation (22) rep-
resent the fact that the standard deviations of ε
d
and
ε
e
are proportional to the module of the angular dis-
placement. The variables k1, k2 and k3 are given by
system (23), considering r
d
= r
e
= r.



















k1 =
r(∆
ˆ
θ
d
+ ∆
ˆ
θ
e
)
b(∆
ˆ
θ
d
− ∆
ˆ
θ
e
)
k2 = θ
t−1
+
r(∆
ˆ
θ
d
− ∆
ˆ
θ
e
)
b
k3 =
b∆
ˆ
θ
e
2(r(∆
ˆ
θ
d
− ∆
ˆ
θ
e
)/b)
2
(23)
3.2 Update Phase: Sensor Model for
Detecting Natural Landmarks
In this work we will use as natural landmarks a set
of straight lines formed by the grooves of the floor
in the environment where the robot will navigate be-
cause, besides being already available in the referred
environment, they are also very common in the real
world.
Due to the choice of the straight lines as land-
marks, the technique adopted to identify them was the
Hough transform. This kind of transform is a method
employed to identify inside a digital image a class of
geometric forms which can be represented by a para-
metric curve (Gonzales, 2000). As what concerns
the straight lines, a mapping is provided between the
Cartesian space (X,Y) and the space of the parame-
ters (ρ,α) where the straight line is defined.
Hough defines a straight line using its common
representation, as equation (24) shows, in which pa-
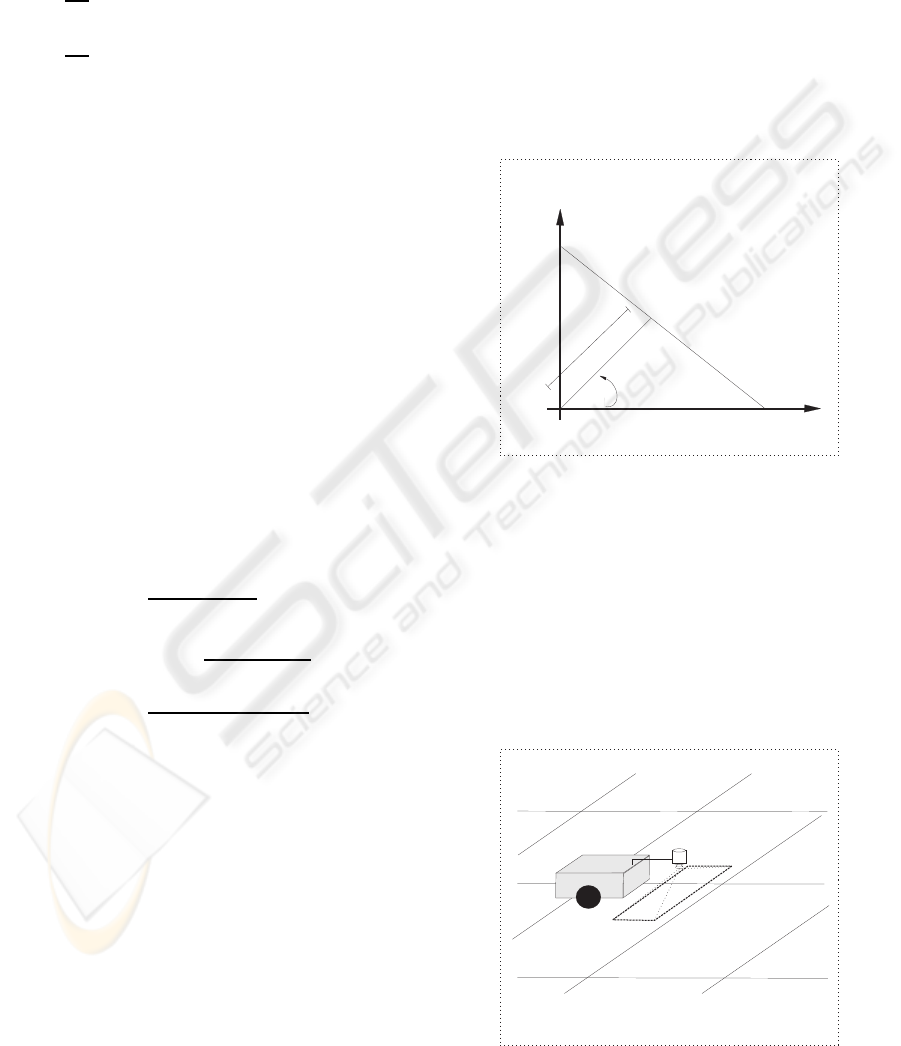
rameter ρ represents the length of the vector and α the
angle this vector forms with axis X. Figure 2 shows
the geometric representation of these parameters.
ρ = xcos(α) + ysin(α) (24)
a
r
X
Y
Figure 2: Parameters of the Hough.
The system discussed in this paper is based in a
robot with differential drive, possessing a rm and sta-
ble camera embedded in its structure, as in Figure 3.
The idea is to use information obtained directly on
the image processing (ρ,α) in the actualization phase
of an Extended Kalman Filter to calculate the robot’s
pose. Thereof, one must deduct the sensor model (that
is, the image processor) in function of the variables of
state.
Figure 3: Robotic system.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
190

Y
x
M
F
y
M
F
F
X
F
X
M
Y
M
q
M
F
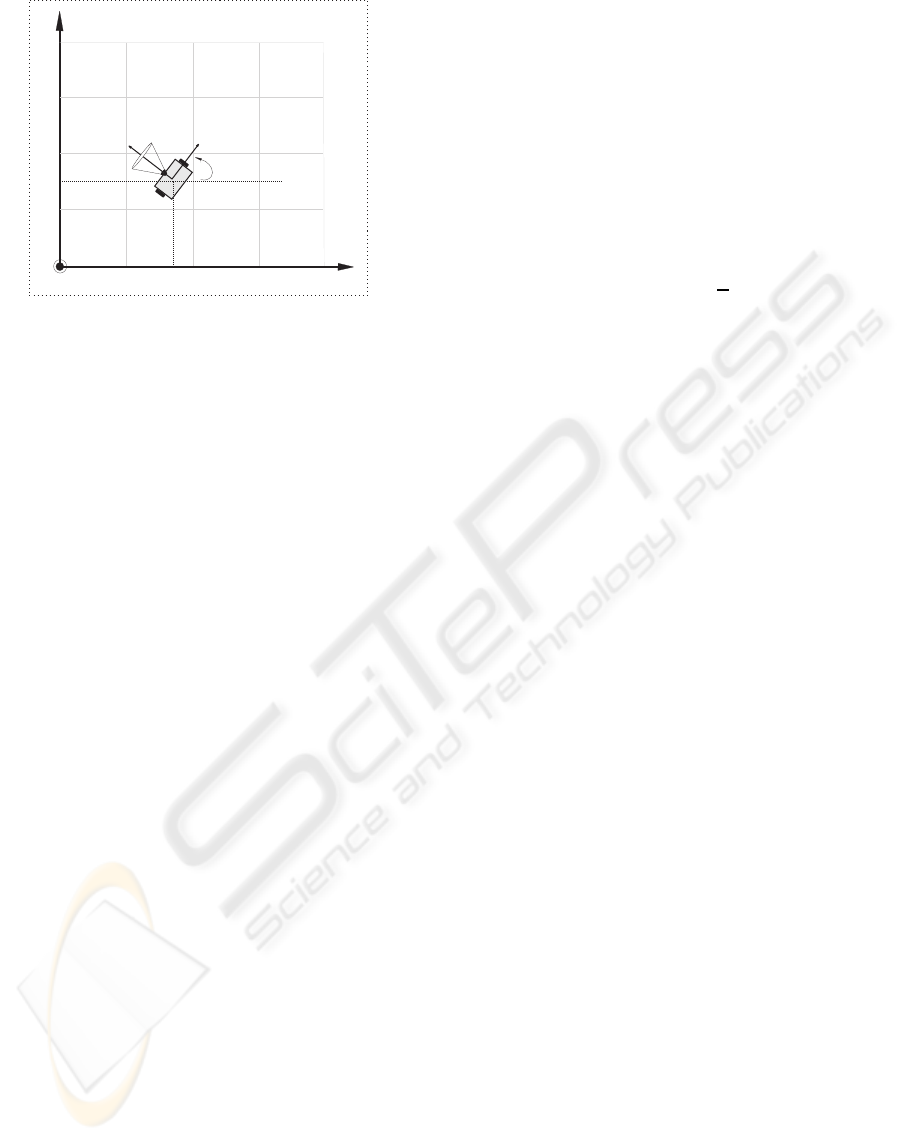
Figure 4: System of Coordinates.
Robot navigates an environment in which the po-
sition of the straight lines of the world (α
F
, ρ
F
) is
known and, at each step, it identifies the descriptors of
the straight lines contained in the image (α
M
, ρ
M
) us-
ing image processing and the parameters of the cam-
era gauging.
Figure 4 illustrates the systems of steady {F} and
mobile { M} coordination used to mathematic deduc-
tion of the sensor model. The point (x
F
M
,y
F
M
) is the
coordinate of origin of the mobile system mapped in
the system of steady and mobile coordinates, while
variable θ
F
M
represents the rotation angle of the sys-
tem of mobile coordinates.
Our point of departure is a simple change map-
ping a point in the system de mobile {M} coordinates
for the system of steady {F} coordinates, as in sys-
tem (25).
(
x
F
= cos(θ
M
F
)x
M
− sin(θ
M
F
)y
M
+ x
F
M
y
F
= sin(θ
M
F
)x
M
+ cos(θ
M
F
)y
M
+ y
F
M
(25)
Using an equation (24) and considering the system
of steady {F} coordinates, we have:
ρ
F
= x
F
cos(α
F
) + y
F
sin(α
F
)
(26)
Also using the definition of system (24), but now
considering the system of mobile {M} coordinates,
we have:
ρ
M
= x
M
cos(α
M
) + y
M
sin(α
M
)
(27)
Replacing (25) in (26) and doing the necessary
equivalences with system (27), we can obtain sys-
tem (28), which represents the sensor module to be
used in the filter.
(
α
M
= α
F
− θ
F
M
ρ
M
= ρ
F
− x
F
M
cos(α
F
) − y
F
M
sin(α
F
)
(28)
In this system, α
F
and ρ
F
are given, because they
represent the description of the map landmark, which
is supposedly known. The equations express the re-
lations among the returned information (α
F
,ρ
F
) and
the height that one wants to estimate (x
M
F
,y
M
F
,θ
M
F
).
One should note that there is a straight relation
among these variables (x
M
F
,y
M
F
,θ
M
F
) and the robot’s
pose (x
R
,y
R
,θ
R
), which is given by system 29.







x
R
= x
M
F
y
R
= y
M
F
θ
R
= θ
M
F
+
π
2
(29)
The model of system 28 is incorporated to the
Kalman Filter through matrix H (equation 8), given
by equation 30.
H =

−cos(θ
F
M
) −sin(θ
F
M
) 0
0 0 −1

(30)
4 RESULTS
The situations presented here have been obtained by
simulation. We tried to use the noise measure of the
sensors consistent to reality. For that, it has been em-
bedded to encoders a noise which standard deviation
is proportional to the amount of read pulses. In the
identification of the parameters of the straight lines ρ
and α, the standard deviation of noise also obeys a
proportion which is ruled by the size that the straight
line occupies in the image.
In the Figures, the hatched rectangle represents
the robot’s real pose, while the continuous rectangle,
the calculated pose.
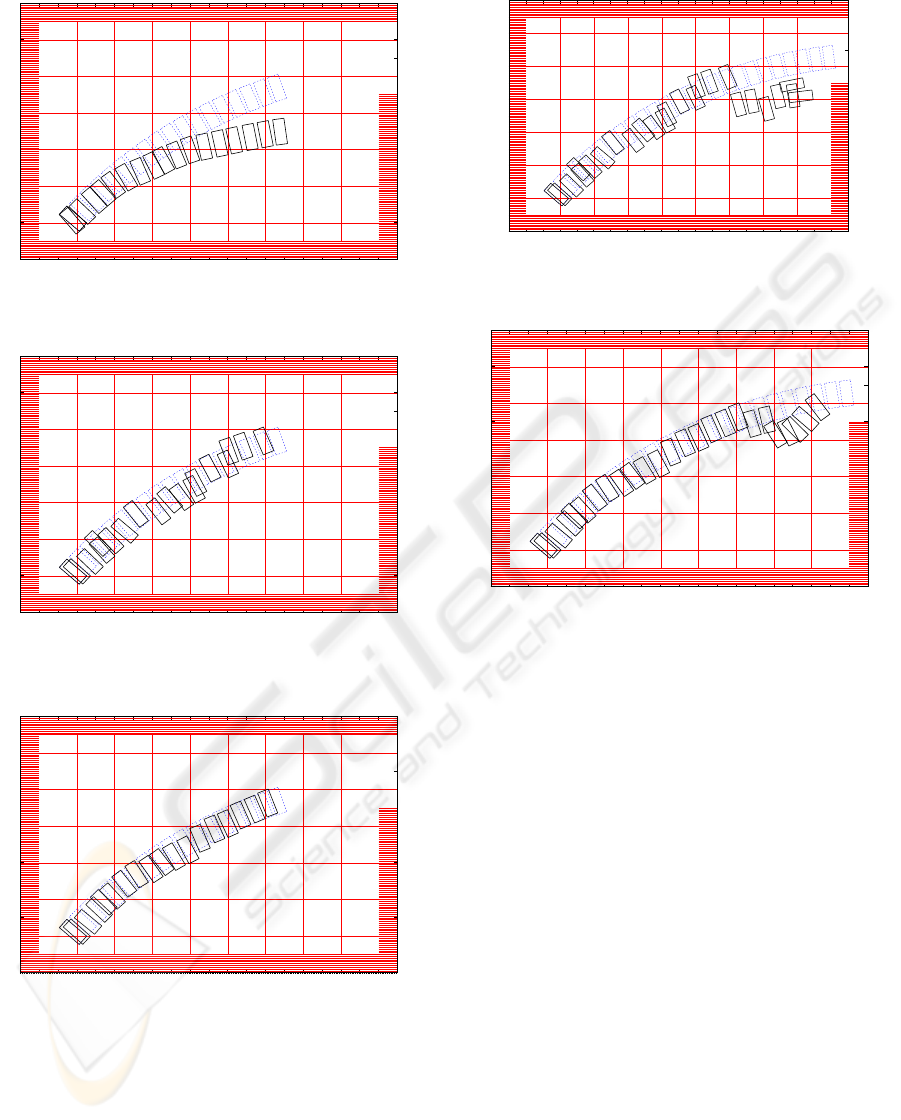
Figure 5 presents the result of the localization sys-
tem us- ing only odometry.
Another localization system largely used has also
been implemented: the localization system using ge-
ometric correction. In this system, at each step the
straight lines are identified and used to calculate the
robot’s pose using trigonometry. When there are
no straight lines, the correction is made by odome-
try(Figure 6).
Finally, in Figure 7 is shown the result of the pose
calculation using the fusion of the data of odometry
and of the landmark detection by EKF.
A particular situation has been implemented to
test the robustness of the localization systems. For
that, it has been introduced to the system a perturba-
tion whenever the robot gets near position (6.5,4.5).
The results coming from the use of geometry and
Kalman are exhibited in Figures 8 and 9.
LOCALIZATION OF A MOBILE ROBOT BASED IN ODOMETRY AND NATURAL LANDMARKS USING
EXTENDED KALMAN FILTER
191

0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
MAPA DO AMBIENTE
Figure 5: Localization by odometry.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
MAPA DO AMBIENTE
Figure 6: Localization by odometry and geometric correc-
tion.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
MAPA DO AMBIENTE
Figure 7: Localization using Extended Kalman Filter.
5 CONCLUSIONS AND
PERSPECTIVES
This paper has proposed a localization system for mo-
bile robots using the Extended Kalman Filter. The
main contribution is the modeling of the optic sensor
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
MAPA DO AMBIENTE
Figure 8: Effect of perturbation: Localization by odometry
and geometric correction.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
MAPA DO AMBIENTE
Figure 9: Effect of perturbation:Localization using Ex-
tended Kalman Filter.
made such a way that it permits using the parameters
obtained in the image processing directly to equations
of the Kalman Filter, without passing any intermedi-
ate phase of pose calculation, or of distance, only with
the available usual information.
When analyzing Figures 5, 6 and 7 one can per-
ceive that the behavior of the localization system us-
ing the Kalman Filter has proved more satisfactory
than those using odometry and geometric corrections.
As what concerns perturbation rejections (Fig-
ures 8 e 9) the system based in Kalman also proved
efficient, for it tends to return to real pose, while the
system based in geometric correction did not exhibit
the same performance.
As future works, we intend to: Implement other
formulations of the Kalman Filter. For example,
the Kalman Filter with Partial Observations; Replace
the Kalman Filter by a Filter of Particles, having in
view that the latter incorporates more easily the non-
linearities of the problem, besides leading with non-
Gaussian noises; Develop this strategy of localization
to a proposal of SLAM (Simultaneous Localization
and Mapping), so much that robot is able of doing its
localization without a previous knowledge of the map
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
192

and, simultaneously, mapping the environment it nav-
igates.
ACKNOWLEDGEMENTS
We thanks CAPES and CNPq by the financial sup-
port.
REFERENCES
Bezerra, C. G. (2004). Localizao de um rob mvel usando
odometria e marcos naturais. Master’s thesis, Univer-
sidade Federal do Rio Grande do Norte, UFRN, Natal,
RN.
Borenstein, J., Everett, H., Feng, L., and Wehe, D. (1997).
Mobile robot positioning: Sensors and techniques.
Journal of Robotic Systems, 14(4):231–249.
Gonzales, R. C. (2000). Processamento de Imagens Digi-
tais. Edgard Blucher.
Kim, S. and Kim, Y. (2004). Robot localization using ultra-
sonic sensors. Proccedings of the 2004 IEEE/RSJ In-
ternational Conference on Inteligent Robots and Sys-
tems, Sendal, Japan.
Kiriy, E. and Buehler, M. (2002). Three-state extended
kalman filter for mobile robot localization. Report
Centre for Intelligent Machines - CIM,McGill Univer-
sity.
Launay, F., Ohya, A., and Yuta, S. (2002). A corridors lights
based navigation system including path definition us-
ing a topologically corrected map for indor mobile
robots. Proceedings IEEE International Conference
on Robotics and Automation, pp.3918-3923.
Lizzaralde, F., Nunes, E., Hsu, L., and J.T., W. (2003). Mo-
bile robot navigation using sensor fusion. Procced-
ings of the 2003 IEEE International Conference on
Robotics and Automation, Taipei, Taiwan.
Park, K. C., Chung, D., Chung, H., and Lee, J. G. (1998).
Dead reckoning navigation mobile robot using an in-
direct kalman filter. Conference on Multi-sensor fu-
sion and Integration for Intelliget Systems, 9(3):107-
118.
Pres, J., Catellanos, J., Montiel, J., Neira, J., and Tards, J.
(1999). Continuous mobile robot localization: Vision
vs. laser. Proccedings of the 1999 IEEE International
Conference on Robotic and Automation.
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
Robotics. MIT Press, 01 edition.
LOCALIZATION OF A MOBILE ROBOT BASED IN ODOMETRY AND NATURAL LANDMARKS USING
EXTENDED KALMAN FILTER
193