DISCRETE-EVENT SIMULATION OF A COMPLEX

INTERMODAL CONTAINER TERMINAL

A Case-Study of Standard Unloading/Loading Processes of Vessel Ships

Guido Maione

DEESD, Technical University of Bari, Viale del Turismo 8, I-74100, Taranto, Italy

Keywords: Container Terminals, Discrete-Event Systems, Simulation, Transport Systems.

Abstract: This paper analyzes the performance of a complex maritime intermodal container terminal. The aim is to

propose changes in the system resources or in handling procedures that guarantee better performance in

perturbed conditions. A discrete-event system simulation study shows that, in future conditions of increased

traffic volumes and reduced available stacking space, more internal transport vehicles, or appropriate

scheduling and routing policies, or an increased degree of automation would improve the performance.

1 INTRODUCTION

In an intermodal container terminal (CT) freight is

organized, stacked, handled and transported in

standard units of a typical container, which is called

TEU (Twenty Equivalent Unit) and which fits to

ships, trains and trucks that are built and work for it.

A maritime CT is usually managed to offer three

main services: a railway/road ‘export cycle’, when

TEUs arrive by trains/trucks and depart on vessel

ships; a railway/road ‘import cycle’, when TEUs

arrive on vessel ships and depart by trains/trucks; a

‘transshipment cycle’, when TEUs arrive on vessel

(feeder) ships and depart on feeder (vessel) ships.

The hub in Taranto is managed by a private

company (Taranto Container Terminal or TCT),

whose primary business is for transhipment, because

of the low quality of railway and road networks

connecting the hub to Italy and the rest of Europe.

The terminal receives ships to a quay and uses

yard blocks to stack full or empty TEUs. Imported

TEUs are unloaded, exported TEUs are loaded,

while in transshipped TEUs both processes occur.

Full TEUs may be imported, exported or

transshipped. Empty TEUs are unloaded from feeder

ships or arrive on trains or trucks; then they are

loaded on vessel ships. So, they are transhipped or

exported.

The typical activities executed by humans and

resources in a transshipment cycle are the following:

 Unloading TEUs from ship by quay cranes;

 Picking-up and transferring TEUs to a yard

block by trailers;

 Picking-up and stacking TEUs in a yard block

by yard cranes;

 Redistributing TEUs in yard blocks by yard

cranes and trailers;

 Picking-up and transferring TEUs to ship by

yard cranes and trailers;

 Loading on ship by quay cranes.

Managing these activities requires an optimized

use of equipment and human operators. Human

supervision is often required to control processes

concurring and competing for the limited number of

available resources. Moreover, efficiency is needed

for services in reduced time without excessive costs:

both the TCT needs to profitably use resources, and

ship companies aim at saving the berthing time/cost.

TCT is expecting a growth in freight volumes

and has recently expanded the yard. But no

investment was made on local land infrastructures.

Not much research was carried out on use of

information and communication technologies or new

control policies to improve efficiency, to the best of

the author knowledge. Improvements can be

achieved for TCT, which is very sensitive to

disturbances and parameter variations (sudden or big

increase of traffic volumes, reduction or

reorganization of yard, changes in berthing spaces,

different routing of trailers, faults and malfunctions).

Then, an intelligent control may guarantee

robustness and a quick reaction to parameter

variations. The aim here is to prove that current

171

Maione G. (2008).

DISCRETE-EVENT SIMULATION OF A COMPLEX INTERMODAL CONTAINER TERMINAL - A Case-Study of Standard Unloading/Loading Processes

of Vessel Ships.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 171-176

DOI: 10.5220/0001499801710176

 SciTePress

organization and control of the main unloading and

loading processes could be not efficient in future

operating conditions. Changing management of

operations is necessary to guarantee good

performance in perturbed conditions.

2 LITERATURE OVERVIEW

Managing a maritime CT is a complex task. Several

analytical models have been proposed as tool for the

simulation of terminals useful to an optimal design

and layout, organization, management and control.

Modelling CTs requires the simulation of many

operations that need coordination to minimize time

and costs. Determining the best management and

control policies is also important (Mastrolilli et al.,

1998). The main problems are: berth allocation;

loading and unloading of ships (crane assignment,

stowage planning); transfer of TEUs from ships to

yard and back; stacking operations; transfer to/from

other transport modes; workforce scheduling.

A thorough literature review on modelling

approaches is given in (Steenken et al., 2004). Two

main classes of modelling approaches can be

highlighted: microscopic and macroscopic methods

(Cantarella et al., 2006). Microscopic models are

generally based on discrete-event system simulation

that may include Petri Nets (Fischer and Kemper,

2000, Liu and Ioannou, 2002), object-oriented

(Bielli et al., 2006) and queuing networks theory

approaches (Legato and Mazza, 2001). Even if high

computational effort may be required, microscopic

simulation explicitly models all activities as well as

the whole system by considering the single TEUs as

entities. Then, it estimates performance as

consequence of different designs and/or

management scenarios.

Macroscopic modelling (de Luca et al., 2005) is

suitable for supporting strategic decisions, system

design and layout, investments on handling

equipment. A network-based approach is presented

in (Kozan, 2000) for optimising efficiency by using

a linear programming method.

3 DEVS MODELLING

A Discrete EVent System (DEVS) specification

technique (Zeigler et al., 2000) completely and

unambiguously represents and controls the terminal

processes.

Atomic dynamic DEVSs model both TEUs

flowing in the system and resources (cranes, trailers,

trucks) used to handle them. DEVSs interact by

transmitting outputs and receiving inputs, which are

all instantaneous events. Timed processes are

defined by a start-event and a stop-event.

For each DEVS, internal events are triggered by

internal mechanisms, external input events are

determined by other DEVSs, and external output

events are generated and directed to other entities.

A DEVS state is changed by an input or when

the time specified before an internal event elapses.

In the first case, an external transition function

determines the state next to the received input; in the

second case, an internal transition function gives the

state next to the internal event. The total state is q =

(s, e), where s is the sequential state and e is the time

elapsed since the last transition.

To summarize, each DEVS is represented as:

DEVS = < X, Y, S,

, ta >

(1)

where X is the set of inputs, Y is the set of outputs, S

is the set of sequential states,

int

:S→S is the internal

transition function,

ext

:Q×X→S is the external

transition function, Q={q=(s,e)|s∈S,0≤e≤ta(s)},

:S→Y is the output function, ta:S→ℜ

is the time

advance function, with ℜ

set of positive real

numbers with 0 included.

The network of DEVS atomic models is used as

a platform for simulating the TCT dynamics. Details

are omitted here for sake of space.

4 SIMULATION ANALYSIS

A simulation study is presented to analyse the

contemporaneous processes of unloading and

loading TEUs from and to a vessel ship.

The simulation model is based on the real TCT

equipment and operation times, which were

statistically observed during steady-state conditions.

The model was developed in a discrete-event

environment by using Arena

(Kelton et al., 1998).

4.1 Experimental Setup

The data used to set up the simulation experiments

refer to the observations recorded during year 2004,

when TCT achieved the maximum productivity

(Table 1). About 14% of TEUs flew through

railway/road transport modes. The numbers of

full/empty TEUs are divided as in Table 2.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

172

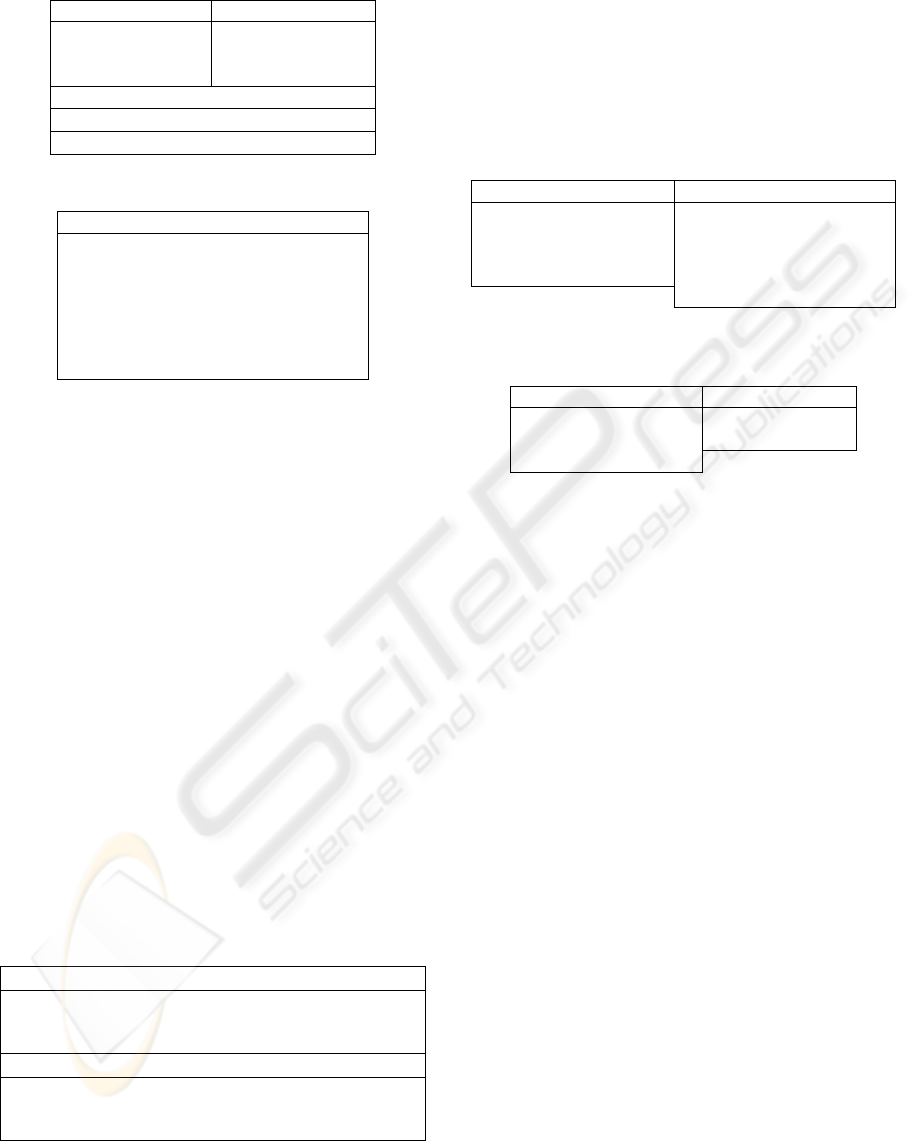
Table 1: Loaded/unloaded TEUs in TCT (2004).

Loaded TEUs Unloaded TEUs

Full

273224

Full

285488

Empty 108172 Empty 96434

Total TL 381396 Total TD 381922

Total T = TL+TD = 763318

TEUs on railway 44486 ≅ 5.8% of T

TEUs on road 64648 ≅ 8.5% of T

Table 2: Flows of containers in TCT (2004).

Containers (Cycle) No.

Full, from vessel to feeder x

Full, from feeder to vessel y

Full, from vessel to train/truck t

Full, from train/truck to vessel z

Empty, from feeder to blocks r

Empty, from train/truck to blocks h

Empty, from blocks to vessel q

Then, we may establish the following relations:

x + y + z = 273224 (2)

q = 108172 (3)

x + y + t = 285488 (4)

r = 96434 (5)

t + z + h = 113134 (6)

r + h = q (7)

where (7) is due to the assumption that no empty

TEU is accumulated and left in the yard blocks.

Then, it is easy to find: x+y = 228658, t = 56830,

z = 44566, r = 96434, h = 11738, q = 108172. The

TEUs separately handled by vessel and feeder ships

were estimated in the ranges in Table 3, because x

and y were assumed between 0 and 228658. Then,

the average number of TEUs handled by vessel (avs)

or feeder ships (afs) was determined by assuming

traffic volumes of 346 vessel and 570 feeder ships in

year 2004. These assumptions were based on the

traffic data available for year 2003 and on the 15.9%

increase in traffic (then in number of ships) in 2004.

Table 3: Containers handled by ships.

Vessels TEUs Est. Range

avs

Unload. x+t [56830,285488] [164,825]

Loaded y+z+q [152738,381396] [441,1102]

Total x+t+y+z+q 438226 1266

Feeders TEUs Est. Range

afs

Unload. y+r [96434,325092] [169,570]

Loaded x [0,228658] [0,401]

Total y+r+x 325092 570

If x = y = 114329, then the flows indicated by

Tables 4 and 5 are obtained, which were used to set-

up the simulation tests. Flows of TEUs from vessel

ships to land are in a ratio 8 to 6 between road and

railway modes, as observed in 2004. Unloaded and

loaded TEUs are 39% and 61% of the total for

vessel ships, 65% and 35% for feeder ships.

Table 4: Containers unloaded (U) and loaded (L) by vessel

ships (F = feeder ships, TA = trains, TU = trucks, E =

blocks for empty TEUs).

U No. (%) L No. (%)

To F 114329 (66.80) From F 114329 (42.81)

To TA 24356 (14.23) From E 108172 (40.50)

To TU 32474 (18.97) From TA 19100 (7.15)

Total 171159 (100) From TU 25466 (9.54)

Total 267067 (100)

Table 5: Containers unloaded (U) and loaded (L) by feeder

ships (V = vessel ships, E = blocks for empty TEUs).

U No. (%) L No.

To V 114329 (54.24) From V 114329

To E 96434 (45.76) Total 114329

Total 210763 (100)

4.2 Simulation Assumptions

Simulation is based on the following assumptions:

 Only 1 vessel ship is berthed, full TEUs are

unloaded, full and empty TEUs are loaded;

1300 TEUs are handled; 508 (39%) are

unloaded, 792 (61%) are loaded, according to

the percentage partitions shown in Table 4;

 The average values of handled TEUs in Table 3

is used, because information about daily

movement or ship size was not available;

 Simulation is limited by the time necessary to

end the unloading and loading processes;

 Transfers from/to the railway connection or the

truck gate, are not considered;

 Operations length and distances travelled are

measured in minutes and meters, respectively.

The model considers four quay cranes: QC1 and

QC2 are for unloading, QC3 and QC4 for loading.

Then, unloaded TEUs are stowed in ship sections

different from those reserved for loaded TEUs, so

that the processes are parallel. Sometimes cranes

sequentially unload and load TEUs, depending on

the stowage plan and on the destinations of TEUs.

A quay crane unloads/loads two TEUs on/from a

trailer in eight steps (Table 6): S1) picking the first

TEU from ship/trailer; S2) moving the crane with

first TEU towards the trailer/ship; S3) releasing the

first TEU on the trailer/ship; S4) moving the crane

back to the ship/trailer; S5) picking the second TEU

from ship/trailer; S6) moving the crane with second

DISCRETE-EVENT SIMULATION OF A COMPLEX INTERMODAL CONTAINER TERMINAL - A Case-Study of

Standard Unloading/Loading Processes of Vessel Ships

173

TEU to the trailer/ship; S7) releasing the second

TEU; S8) moving the crane back to the ship/trailer.

Table 6: Operation cycle of quay cranes.

Step Duration

S1 Tria(0.4375,0.5,0.75)

S2 0.333

S3 Tria(0.4375,0.5,0.75)

S4 0.667

S5 Tria(0.4375,0.5,0.75)

S6 0.333

S7 Tria(0.4375,0.5,0.75)

S8 0.667

The triangular distribution is used because only

the estimates of the minimum, most likely and

maximum values (shown in this order) of the

processing times are known. Simple translational

return steps last longer (twice) than transfer steps

because the crane is more unstable without TEUs.

Five trailers serve each quay crane. Each set of

five trailers is indicated with a unique symbol: TR1,

TR2, TR3, TR4 are associated to QC1, QC2, QC3,

QC4, respectively. Each trailer always transports

two TEUs, with a speed of 300 m/minutes (400

m/minutes when travelling unloaded). The closest

trailer is selected for a task between ship and yard.

Before being loaded, exported and transshipped

TEUs are stacked in blocks close to the quay area,

while imported TEUs are stacked in blocks close to

the land connections. Only one yard crane works on

each block for unloaded TEUs from ships: YC1

serves transhipped TEUs; YC2/YC3 serves exported

TEUs. Two yard cranes (YC4 and YC5 or YC6 and

YC7) work for each block for TEUs to be loaded:

YC4 serves empty TEUs, YC5 serves full TEUs;

YC6 and YC7 serve full TEUs. YC7 has priority

with respect to YC6 because it is closer to the quay.

TEUs picked by YC4 and YC5 are loaded by QC3,

those picked by YC6 and YC7 are loaded by QC4.

A yard crane unloads/loads two TEUs in/from a

yard block from/to a trailer in eight steps (Table 7).

Table 7: Operation cycle of yard cranes.

Step Duration

S1 Tria(0.125,0.375,0.625)

S2 0.25

S3 Tria(0.125,0.375,0.625)

S4 0.5

S5 Tria(0.125,0.375,0.625)

S6 0.25

S7 Tria(0.125,0.375,0.625)

S8 0.5

A typical and important performance index is the

Ship Turn-around Time (STT), the average time

spent by a berthed ship to unload and load TEUs.

STT is measured between ship arrival and departure.

Minimizing STT is the main objective of every

terminal management. An empiric relation to

calculate the minimum STT value is:

STT

min

= nc / (ct × nqc)

(8)

where nc is the number of unloaded/loaded TEUs, ct

is the cycle time (the number of moves/hour of a

quay crane), and nqc is the number of quay cranes.

Equation (8) gives a reference for the terminal

productivity. Namely, it does not consider the

dependence of ct on nqc, due to the interaction

between nqc and the handling capacity in the limited

quay space, and the effects of internal transfers.

Figure 1 gives the STT when nc = 3400 and ct = 42

hours

-1

. Equation (8) can also be used to estimate the

necessary nqc to achieve a desired STT.

Figure 1: STT as function of nqc.

Assuming the most likely value ct = 30 hours

-1

, if

= 508 and nc

= 792 are the unloaded and loaded

TEUs, and if nqc

= nqc

= 2 are the cranes used for

the two processes, then a reference limit for STT is:

STT

min

= max{ nc

/(ct×nqc

); nc

/(ct×nqc

)}

= max{8.5; 13.2} = 13.2 hours.

(9)

Finally, note that performance is affected by the

partial automation of processes, the humans’

cooperation, the non-optimal ship distribution of

TEUs and weather conditions.

4.3 Simulation Results

Ten simulation runs were executed, using different

seeds for generating random variables, in order to

obtain sufficient results for a statistical evaluation.

Each run was terminated after 1300 unloaded and

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

174

loaded TEUs. The system state was initialized at the

beginning of each run, to start from the same

condition. Statistics were also initialized to have

results independent on the data obtained from

precedent runs. Initializations guarantee statistically

independent and identically distributed replications

of the terminating simulation.

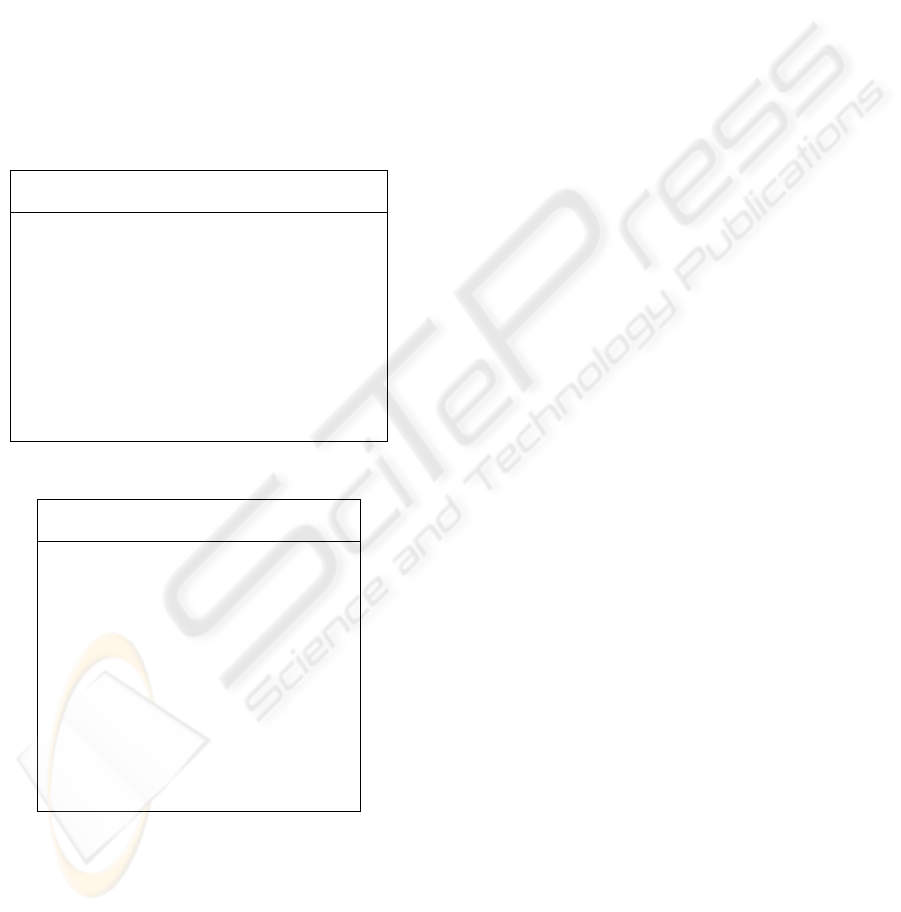
STT was measured at the end of each run (Figure

2). The minimum, maximum, and average values

were 891, 902, and 898, i.e. about 15 hours.

Figure 2: Measured STT in 10 simulation runs.

These results validate the model because:

 They are below the real TCT performance,

because only 1 ship/day is served in standard

real operating conditions;

 The measured values of STT are greater than

the lower theoretical limit established by (9).

STT can be also measured for ships of different

capacity or with a distribution of TEUs different

from that in Table 4. If we let 1300 TEUs equally

distributed between the four quay cranes, we obtain

the results in Figure 3. The minimum, maximum and

average values of STT were, respectively, 714, 723,

and 718, that correspond to about 12 hours.

Figure 3: Measured STT in 10 simulation runs (TEUs

equally distributed between quay cranes).

Performance indices were measured for critical

resources like trailers and cranes: waiting times in

queue; number of entities in queue; resource

utilization. The associated statistics were: the

average value in 10 runs; the minimum average

value in a single run; the maximum average value in

a single run; the maximum value.

Table 8 shows the waiting times. For unloading

processes, TEUs may wait for the following busy

resources: a) TR1 or TR2, when being on QC1 or

QC2; b) YC1, YC2, YC3, when being on TR1 or

TR2. For loading processes, TEUs may wait for: a)

TR3, when being on YC4 used for empty TEUs; b)

TR3, when being on YC5 used for full TEUs (busy

resource TR3*); c) TR4, when being on YC6 used

for full TEUs; d) TR4, when being on YC7 used for

full TEUs (busy resource TR4*); e) QC3 or QC4,

when being on trailers TR3 or TR4.

Table 8: Waiting times in queue of busy resources.

Busy

Res.

Average Min.

Aver.

Max.

Aver.

Max.

Value

TR1 0.0788 0.00 0.1393 5.0002

TR2 0.0807 0.00 0.1613 4.7440

YC1 3.5193 2.5625 4.6946 17.7338

YC2 0.0612 0.00 0.1264 1.9246

YC3 0.0989 0.00 0.1965 2.0696

TR3 1.0662 1.0013 1.1135 6.8421

TR3* 28.4835 28.2937 28.6313 770.4400

TR4 5.1725 5.1165 5.2450 418.2100

TR4* 1.2628 1.21478 1.3079 7.8171

QC3 7.2326 7.0881 7.3267 10.5871

QC4 5.9521 5.8538 6.0713 10.2105

The average waiting times of TR1 and TR2 are

below 5 seconds, and then delays in unloading TEUs

due to the waiting of trailers below the quay cranes

can be neglected. So, more trailers are not necessary

for unloading in the simulated conditions. On the

contrary, the results for TR3, TR3*, TR4, TR4*

show that the loading process waits for long time

when yard cranes are used. Thus, at least one more

trailer should be used.

The large values for TR3* and TR4 were

obtained because of the priority given to empty with

respect to full TEUs, and because of the priority of

selecting the closest yard crane YC7 instead of YC6.

If we consider the interactions of trailers with

yard cranes during the unloading process, high

waiting times are observed for YC1 only, because

most of the unloaded TEUs were stacked in the

block served by YC1. More yard cranes would

speed-up the stacking process, but they are not

necessary since the number and speed of trailers is

DISCRETE-EVENT SIMULATION OF A COMPLEX INTERMODAL CONTAINER TERMINAL - A Case-Study of

Standard Unloading/Loading Processes of Vessel Ships

175

sufficient to guarantee fast and almost continuous

unloading operations by the quay cranes.

Long times are recorded for trailers when

waiting for quay cranes to load TEUs (more than 7

minutes for QC3 and about 6 minutes for QC4).

Then, one more trailer could help operations in the

yard area, because the maximum number of queued

trailers below a quay crane is three (see Table 9),

such that the other two are available for yard cranes.

Table 9 shows the results for the number of

entities in queue (the minimum value is always 0).

Table 10 shows the utilization of resources, i.e.

the percentage number of busy units or the

percentage busy time for single-unit resources (the

minimum is always 0, the maximum is always 1).

Table 9: Number of entities in queue of busy resources.

Busy

Res.

Average Min.

Aver.

Max.

Aver.

Max.

Value

TR1 0.0111 0.00 0.0199 1.0000

TR2 0.0114 0.00 0.0230 1.0000

YC1 0.6708 0.4637 0.9167 6.0000

YC2 0.0026 0.00 0.0062 1.0000

YC3 0.0056 0.00 0.0109 1.0000

TR3 0.2018 0.1911 0.2100 1.0000

TR3* 0.8882 0.8837 0.8906 1.0000

TR4 0.5703 0.5653 0.5770 1.0000

TR4* 0.1392 0.1339 0.1446 1.0000

QC3 1.5947 1.5753 1.6095 3.0000

QC4 1.3124 1.2990 1.3337 3.0000

Table 10: Utilization of resources.

Resource Average Min.

Aver.

Max.

Aver.

QC1 0.6104 0.6019 0.6218

QC2 0.6122 0.6036 0.6265

QC3 0.9919 0.9913 0.9926

QC4 0.9378 0.9324 0.9439

TR1 0.4818 0.4614 0.5013

TR2 0.4828 0.4660 0.5049

TR3 0.9897 0.9890 0.9899

TR4 0.9360 0.9307 0.9425

YC1 0.5712 0.5302 0.5970

YC2 0.1150 0.0892 0.1692

YC3 0.1617 0.1055 0.1812

YC4 0.8642 0.8612 0.8724

YC5 0.9825 0.9818 0.9831

Results for quay cranes indicate that unloading

with QC1 and QC2 terminates before loading with

QC3 and QC4. QC3 is used more than QC4 because

of the high number of empty TEUs. Considerations

about yard cranes are similar. Trailers TR1 and TR2

complete their tasks much earlier than TR3 and TR4,

which are practically always busy. Then, the

transport processes could benefit from more trailers.

5 CONCLUSIONS

This paper presents simulates a maritime terminal

container (TCT) in standard operating conditions.

Results prove the benefit from new control strategies

different from those currently used. A new control

approach could reduce terminal operating cycles in

standard and, above all, in perturbed operating

conditions.

REFERENCES

Bielli, M., Boulmakoul, A., Rida, M., 2006. Object

oriented model for container terminal distributed

simulation. European Journal of Operational

Research, Vol. 175, No. 3, pp. 1731-1751.

Cantarella, G.E., Cartenì, A., de Luca, S., 2006. A

comparison of macroscopic and microscopic

approaches for simulating container terminal

operations. In Proc. of EWGT2006 Joint conference,

Bari, Italy, 27-29 Sept. 2006.

de Luca, S., Cantarella, G.E., Cartenì, A., 2005. A

macroscopic model of a container terminal based on

diachronic networks. In Proc. Second Workshop on

the Schedule-Based Approach in Dynamic Transit

Modelling, Ischia, Naples, Italy, 29-30 May 2005.

Fischer, M., Kemper, P., 2000. Modeling and Analysis of

a Freight Terminal with Stochastic Petri Nets. In Proc.

of 9th IFAC Int. Symp. Control in Transp. Systems,

Braunschweig, Germany, vol. 2, pp. 195-200.

Kelton, W.D., Sadowski, R.P., Sadowski, D.A., 1998.

Simulation with Arena, McGraw Hill, New York.

Kozan, E., 2000. Optimising container transfers at

multimodal terminals. Mathematical and Computer

Modelling, Vol. 31, No. 10-12, pp. 235-243.

Legato, P., Mazza, R.M., Sept. 2001. Berth planning and

resources optimisation at a container terminal via

discrete event simulation. European Journal of

Operational Research, Vol. 133, No. 3, pp. 537-547.

Liu, C.I., Ioannou, P.A., 2002. Petri Net Modeling and

Analysis of Automated Container Terminal Using

Automated Guided Vehicle Systems. Transportation

Research Record, No. 1782, pp. 73-83.

Mastrolilli, M., Fornara, N., Gambardella, L.M., Rizzoli,

A.E., Zaffalon, M., 1998. Simulation for policy

evaluation, planning and decision support in an

intermodal container terminal. In Proc. Int. Workshop

Modeling and Simulation within a Maritime

Environment, Riga, Latvia, 6-8 Sept. 1998, pp. 33-38.

Steenken, D., Voss, S., Stahlbock, R., 2004. Container

terminal operation and operations research - a

classification and literature review. OR Spectrum, 26,

pp. 3-49.

Zeigler, B.P., Praehofer, H., Kim, T.G., 2000. Theory of

Modelling and Simulation, Academic Press. New

York, 2

ed..

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

176