AN EVOLUTIONARY ALGORITHM FOR UNICAST/ MULTICAST
TRAFFIC ENGINEERING
Miguel Rocha, Pedro Sousa
Dep. Informatics/ CCTC, Universidade do Minho, Campus de Gualtar, Braga, Portugal
Paulo Cortez
Dep. Information Systems/ Algoritmi, Universidade do Minho, Campus de Azurem, Guimaraes, Portugal
Miguel Rio
Dep. Electric and Electronic Engineering, University College London, Torrington Place, London, U.K.
Keywords:
Traffic engineering, Multicast content, Evolutionary Algorithms, OSPF.
Abstract:
A number of Traffic Engineering (TE) approaches have been recently proposed to improve the performance
of network routing protocols, both developed over MPLS and intra-domain protocols such as OSPF. In this
work, a TE approach is proposed for routing optimization in scenarios where unicast and multicast demands
are simultaneously present. Evolutionary Algorithms are used as the optimization engine with overall network
congestion as the objective function. The optimization aim is to reach a set of (near-)optimal weights to
configure the OSPF protocol, both in its standard version and also considering the possibility of using multi-
topology variants. The results show that the proposed optimization approach is able to obtain networks with
low congestion, even under scenarios with heavy unicast/multicast demands.
1 INTRODUCTION
A new plethora of network services is putting strong
requirements on TCP/IP networks, for which these
were not initially designed. Many of these ser-
vices will need a multicast enabled network with de-
manding quality of service (QoS) constraints in the
end-to-end data delivery. The advent of 3-play ser-
vice providers, where the same entity is involved
in the network and TV provision is just the first of
these scenarios. Interactive TV, virtual reality, video-
conferencing, video games or video surveillance are
just some of the applications that would gain from
QoS enabled multicast content delivery. In these sce-
narios, data needs to arrive to a set of users with mini-
mal loss (therefore requiring minimization of conges-
tion) and with acceptable end-to-end delays.
Multicast has been present for a while in TCP/IP
networks, but its widespread use has never occurred
in the Internet. It is, however, used in closed TCP/IP
networks where its scalability problems are not a de-
terrent. In fact, manyIPTV and video-on-demandser-
vices operate in closed networks using multicast to
save bandwidth and enhance QoS levels.
In this context, Traffic Engineering (TE) tech-
niques can be used to improve network performance
by achieving near-optimal configurations for rout-
ing protocols. TE approaches can be classified into:
Multi-Protocol Label Switching (MPLS) (Davie and
Rekhter, 2000)(Awduche and Jabbari, 2002) based
and pure IP-based intra-domain routing protocols.
With MPLS, packets are encapsulated with labels at
ingress points, that can be used to route these pack-
ets along an explicit label-switched path). Together
with resource reservation mechanisms, these capabil-
ities are able to support stringent end-to-end band-
width guarantees for multicast content delivery. How-
ever, the use of MPLS presents significant drawbacks:
firstly, it adds significant complexity to the model,
since per-flow state has to be stored in every router
of the path; secondly, MPLS failure recovery mecha-
nisms are considerably more complex than the typical
router convergence ones; finally, it represents a con-
siderable network management overhead.
As regards intra-domain routing protocols, the
most commonly used today is Open Shortest Path
First(OSPF)(Thomas II, 1998). Here, the adminis-
trator assigns weights to each link in the network,
238
Rocha M., Sousa P., Cortez P. and Rio M. (2008).
AN EVOLUTIONARY ALGORITHM FOR UNICAST/ MULTICAST TRAFFIC ENGINEERING.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 238-243
DOI: 10.5220/0001501602380243
Copyright
c
 SciTePress

which are then used to compute the best path from
each source to each destination using the Dijkstra al-
gorithm (Dijkstra, 1959). The results are then used to
compute the routing tables in each node.
A number of studies have proposed TE procedures
which optimize the weights of intra-domain routing
protocols to achieve near optimal routing, taking as
input the expected traffic demands. This was the ap-
proach taken by Fortz and Thorup (2000) where this
task was viewed as an optimization problem by defin-
ing a cost function that measured network congestion.
The authors proved that this task is a NP-hard prob-
lem and proposed some local search heuristics that
compared well with the MPLS model. Another ap-
proach was the use of Evolutionary Algorithms (EAs)
to improve these results (Ericsson et al., 2002). Ad-
ditional research has been carried out with the objec-
tive of pursuing multiconstrained QoS optimization,
where both traffic demands and delay requirements
are considered in the optimization of routing configu-
rations for unicast traffic (Rocha et al., 2006).
In this paper, EAs are employed to reach OSPF
weights that optimize network congestion, taking into
account both unicast and multicast demands of a
given domain. This work is based on the reasoning
that in the optimization process both the unicast and
multicast demands should be considered simultane-
ously, in contrast with previous work where optimiza-
tion is performed in two distinct phases, the first for
unicast traffic and the second devoted to multicast op-
timization (Wang and Pavlou, 2007).
2 PROBLEM FORMULATION
2.1 Unicast Traffic
In this section, a model for a network only with uni-
cast traffic demands will de described. This is based
on the framework proposed in (Fortz and Thorup,
2000). The general routing problem (Ahuja et al.,
1993) that underpins this work represents routers and
links by a set of nodes (N) and arcs (A) in a directed
graph G = (N,A). In this model, c
a
represents the
capacity of each link a ∈ A. A demand matrix D is
available, where each element d
st
represents the traf-
fic demand between nodes s and t. For each arc a,
the variable f
(st)
a
represents how much of the traffic
demand between s and t travels over arc a. The to-
tal unicast load on each arc a (l
a
) can be defined as:
l
a
=
∑
(s,t)∈N×N
f
st
a
while the link utilization rate u
a
is given by: u
a
=
l
a
c
a
. It is then possible to define a
congestion measure for each link: Φ
a
= p(u
a
). us-
ing a penalty function p that has small values near 0,
but as the values approach the unity it becomes more
expensive and exponentially penalizes values above 1
(Fortz and Thorup, 2000).
In OSPF, all arcs have an integer weight, used by
each node to calculate the shortest paths to all other
nodes in the network, using the Dijkstra algorithm
(Dijkstra, 1959). The traffic from a given source to a
destination travels along the shortest path. If there are
two or more paths with equal length, traffic is evenly
dividedamong the arcs in these paths (load balancing)
(Moy, 1998). Let us assume a given a weight assign-
ment, and the correspondingvalues of u
a
. In this case,
the total routing cost is expressed by Φ =
∑
a∈A
Φ
a
for
the loads and penalties (Φ
a
) calculated based on the
given OSPF weights. In this way, the OSPF weight
setting problem is equivalent to finding the optimal
weight value for each link, in order to minimize Φ.
The congestion measure can be normalized (Φ
∗
) over
distinct scenarios to values in the range [1,5000]. It
is important to note that in the case when all arcs are
exactly full (l
a
= c
a
), the value of Φ
∗
is 10
2
3
, a value
that will be considered a threshold that bounds the ac-
ceptable working region of the network.
2.2 Multicast Demands
A model that considers only multicast traffic in the
network will be described, that is based on a the work
by Wang and Pavlou (2007) . If there are unicast and
multicast demands, this model can be used to perform
a two-step optimization process (explained in the next
section). Consider, as before, a network topology
G = (N,A), with arc capacities (c
a
). The multicast de-
mands are given for a set of G groups, where for each
group g ∈ G the following parameters are defined: a
root node r
g
, a bandwidth demand M
g
and a a set of
receivers (V
g
). The multicast optimization problem is
typically defined as the computation of a bandwidth
constrained Steiner tree, with the objective of mini-
mizing overall bandwidth consumption, using integer
programming. The target is to instantiate a number of
binary decision variables: y
g
a
, are equal to 1 if link a is
included in the multicast tree for group g; and x
g,k
a
are
equal to 1 if link a is included in the multicast tree for
group g, in the branch from the root node to receiver
k. The objective function is to minimize the overall
bandwidth consumption (L1):
L1 =
∑
g∈G
∑
a∈A
M
g
× y
g
a
(1)
The deployment of the obtained Steiner trees can
be enforced by using an explicit routing overlay,
through MPLS on a per-group basis. An alterna-
AN EVOLUTIONARY ALGORITHM FOR UNICAST/ MULTICAST TRAFFIC ENGINEERING
239

tive with some advantages, previously discussed, is to
consider that the routing will be achieved by using an
intra-domain protocol such as OSPF. In this case, the
tree for a given group will be built from the shortest
paths between the root node and each receiver. There-
fore, the values assigned to y
g
a
variables will be com-
puted as follows: y
g
a
is equal to 1 if link a is in the
shostest path from the root node g to at least one of
the receivers in V
g
, and is equal to 0 otherwise.
In previous work (Wang and Pavlou, 2007), EAs
have been proposed to optimize OSPF weights for
multicast traffic. The objective function used in this
case is based on the overall network load (L1) but also
on the excessive bandwidth allocated to overloaded
links (L2), that can is given by:
L2 =
∑
a∈A
[w
a
∑
g∈G
(M
g
× y
g
a
) − c
a
] (2)
w
a
=

0, if
∑
g∈G
M
g
× y
g
a
≤ c
a
1, otherwise
(3)
The EA’s fitness is, therefore, given by:
f(L1,L2) =
µ
α× L1 + β × L2
(4)
where µ, α and β are constants, whose values are set
to 10
7
, 1 and 10 respectively.
2.3 Unified Model with Unicast and
Multicast Demands
In this work, a unified approach will be proposed that
is able to reach OSPF weights that optimize the net-
work congestion measure, simultaneously consider-
ing unicast and multicast demands. In this case, the
multicast load for a given link a can be computed as:
ml
a
=
∑
g∈G
M
g
× y
g
a
. The values of y
g
a
will be cal-
culated from the OSPF weights as explained in the
previous section. So, the total load on a given arc a is
given by: l
a
= ml
a
+ ul
a
, where ul
a
is the unicast load
in arc a (given by l
a
in the previous section). It should
noted that l
a
here takes the meaning of the total load
in the network, while in Section 2.1 l
a
is only used for
unicast loads since in that case those were the only
loads considered. After calculating the overall values
of l
a
for all links, the process proceeds as described in
Section 2.1, in order to reach the normalized conges-
tion measure Φ
∗
.
Another interesting measure of the network per-
formance in this scenario is the excessive bandwidth
in overloaded links (BOL). This is a generalization of
L2 but now applied to the global loads and not only to
the multicast traffic. This is defined as:
BOL =
∑
a∈A
z
a
(l
a
− c
a
) (5)
z
a
=

0, if l
a
≤ c
a
1, otherwise
(6)
3 OPTIMIZATION ALGORITHMS
3.1 Evolutionary Algorithms
Evolutionary Algorithms (EAs) (Michalewicz, 1996)
are a popular family of optimization methods, in-
spired in the biological evolution. These methods
work by evolving a population, i.e. a set of individu-
als, each encoding solutions to a target problem in an
artificial chromosome. Each individual is evaluated
through a fitness function, that assigns it a numeri-
cal value, corresponding to the quality of the encoded
solution. EAs are stochastic methods due to their se-
lection process. In fact, individuals selected to cre-
ate new solutions are taken from the population us-
ing probabilities. Highly fit individuals have a higher
probability of being selected, but the less fit still have
their chance.
In the proposed EA, each individual encodes a so-
lution in a direct way, i.e. as a vector of integer val-
ues, where each value corresponds to the weight of an
arc in the network (the values range from 1 to w
max
).
Therefore, the size of the individual equals the num-
ber of links in the network. If multiple topologies are
used, i.e. different sets of weights for unicast and mul-
ticast, the size of the individual is twice the number of
links and the two sets of weights are encoded linearly,
i.e. the first L genes encode the weights for unicast
traffic, while the latter L links encode the weights for
multicast (L is the number of links).
The weight values for individuals in the initial
population are randomly generated, taken from a
uniform distribution. In order to create new solu-
tions, several reproduction operators were used, more
specifically two mutation and one crossover operator:
• Random Mutation, replaces a given weight value
by a random value, within the allowed range;
• Incremental/decremental Mutation, replaces a
given weight value w by w+ 1 or by w− 1 (with
equal probabilities);
• Uniform crossover, a standard crossover operator
(Michalewicz, 1996).
The operators are all used to create new solutions
with equal probabilities. The selection procedure is
done by converting the fitness value into a linear rank-
ing in the population, and then applying a roulette
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
240

wheel scheme. In each generation, 50% of the indi-
viduals are selected from the previous generation, and
50% are bred by the application of the genetic oper-
ators over selected parents. A population size of 100
individuals was considered.
3.2 Optimization Approaches
Three distinct optimization approaches are compared,
with the aim to optimize OSPF weights in networks
where both unicast and multicast demands are avail-
able. All these methods use EAs as the optimiza-
tion engine. The first method is a 2-step optimization
process (2S), based on the proposal from Section 2.2
(Wang and Pavlou, 2007), that can be described as:
1. the OSPF weights are optimized (using EAs) to
minimize congestion penalties (Φ
∗
) only taking
into account the unicast demands;
2. the bandwidths used for each link in unicast traffic
are deduced from the link capacities;
3. a second optimization process is conducted,
where a different set of weights is calculated from
multicast traffic only, by running a new EA with
f(L1,L2) (Equation 4) as the fitness function.
This method assumes that a protocol that allows
multiple sets of weights, each for a distinct type of
traffic, is deployed. This is the case, for instance, of
the multi-topology protocol MT-OSPF (Psenak et al.,
2006). The remaining alternatives are based on the
model proposed in Section 2.3. Using this model, two
different optimization approaches may be followed:
• Single topology (ST), i.e. a single set of OSPF
weights is used for both types of traffic demands;
• Multiple topologies (MT), i.e. two sets of OSPF
weights are used, one for unicast traffic and the
other for multicast demands. In this case, as be-
fore, a multi-topology protocol has to be used.
4 EXPERIMENTS AND RESULTS
4.1 Experimental Setup
To evaluate the proposed algorithms, a number of ex-
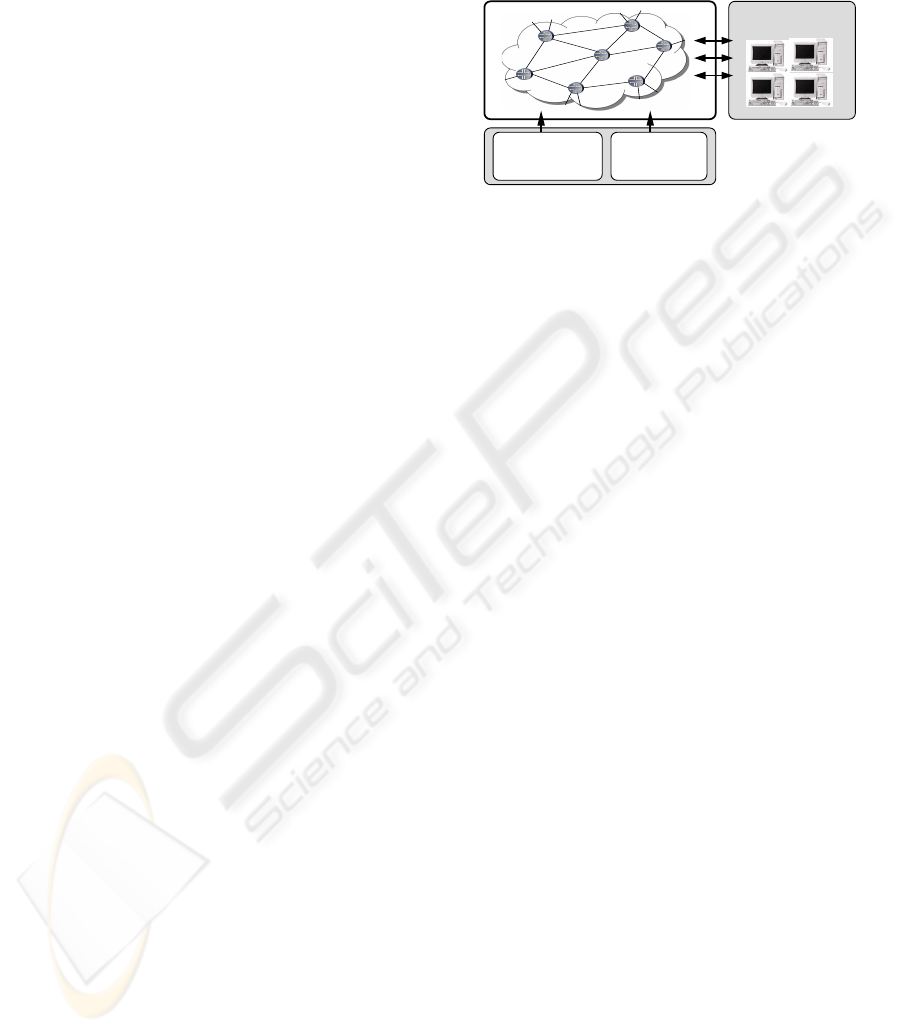
periments were conducted. The experimental plat-
form used in this work is presented in Figure 1. All al-
gorithms and the OSPF routing simulator were imple-
mented using the Java language. A set of 3 network
topologies was created using the Brite topology gen-
erator (Medina et al., 2001), varying the number of
nodes (N = 30,50,80) and the average degree of each
node was kept in (m = 4). This resulted in networks
ranging with 110, 190 and 310 links, respectively.
OSPF Scenario #n
ComputingCluster
OSPF Routing Simulator
EA
OSPF Weight
Setting Module
Generator
Brite Topology
Unicast and
Multicast
Demands
Network Generator
Figure 1: Experimental platform for EA’s performance eval-
uation.
The link bandwidth (capacity) was generated by a
uniform distribution between 1 and 10 Gbits/s. The
networks were generated using the Barabasi-Albert
model, using a heavy-tail distribution and an incre-
mental grow type (parameters HS and LS were set to
1000 and 100). Next, the unicast demand matrices
(D) were generated (two distinct matrices for each
network). A parameter (D
p
) was considered, repre-
senting the expected mean of congestion in each link
(values for D
p
were 0.2 and 0.3).
The generation of the multicast traffic demands
was based on the following: Firstly, for each network
the number of groups G was set equal to the number
of nodes. The root node for each group was randomly
chosen from the set of nodes (with equal probabili-
ties). For each group, the number of receivers was
generated from the range [2,n/2], where n is the num-
ber of nodes. The set of receiversV
g
was created with
the given cardinality, by randomly selecting a set of
nodes different from the root. Finally, the demand M
g
was generated taking a parameter (R) into account. R
is defined as the ratio between the total multicast de-
mands and the total unicast demands. Given R and
given the unicast demands, a target is calculated for
the total multicast demands. The group demands are
generated by dividing the target value by the different
groups in an uneven way, so that groups with differ-
ent demands are created resulting in a more plausi-
ble scenario. By using R, a better understanding of
the results is possible since an approximate idea of
the trade-offsbetween unicast and multicast is known.
The values of R used were 1 and 0.5.
The termination criteria for all optimization ap-
proaches consisted in a maximum number of solu-
tions evaluated. This value ranged from 100000 to
300000, increasing linearly with the number of links.
For all cases, w
max
was set to 20 and 20 runs were
executed and the results presented are the means.
AN EVOLUTIONARY ALGORITHM FOR UNICAST/ MULTICAST TRAFFIC ENGINEERING
241

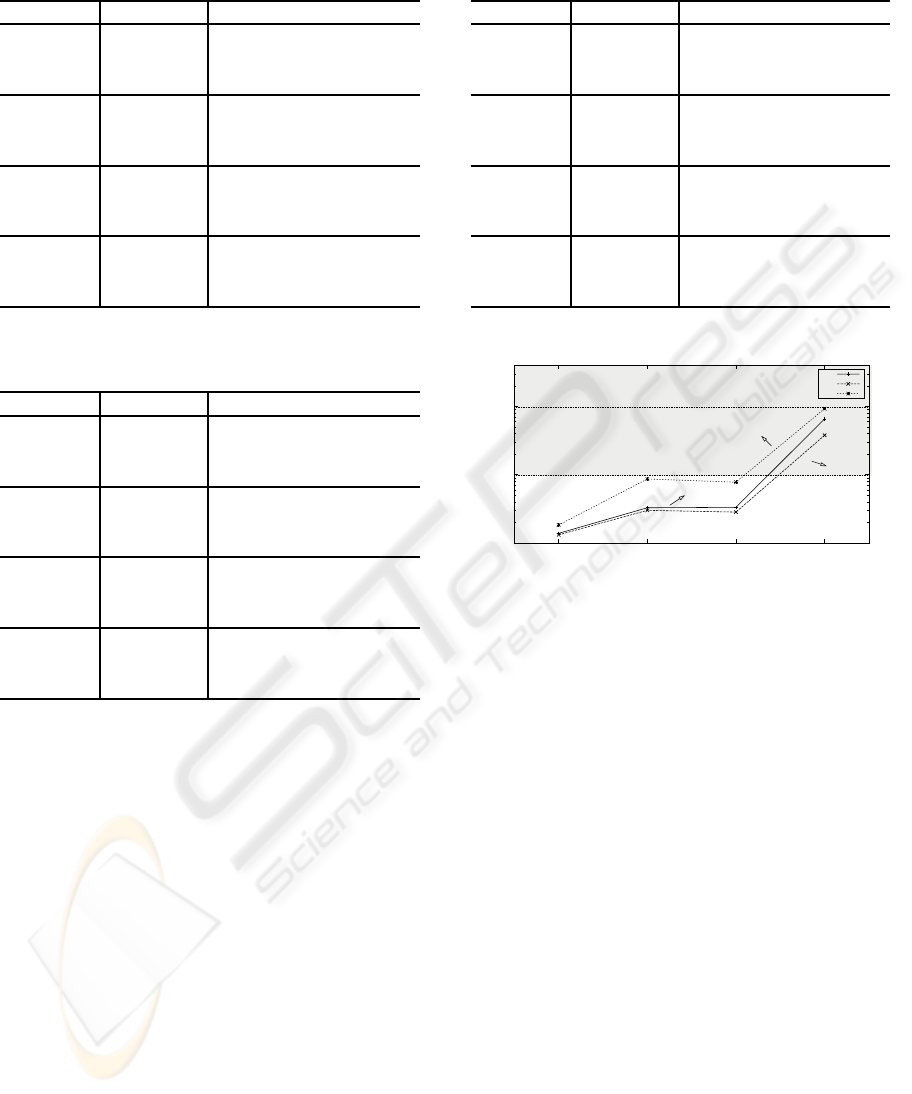
Table 1: Results for the network with 30 nodes.
Demands Metric ST MT 2S
D = 0.2 Φ
∗
1.38 1.31 1.83
R = 0.5 BOL 0 0 42
L1 (×10
5
) 1.10 1.09 0.96
D = 0.2 Φ
∗
3.27 3.00 8.66
R = 1.0 BOL 160 156 1138
L1 (×10
5
) 2.11 2.11 1.97
D = 0.3 Φ
∗
3.32 2.83 7.78
R = 0.5 BOL 257 128 875
L1 (×10
5
) 1.50 1.54 1.39
D = 0.3 Φ
∗
66.2 38.0 93.5
R = 1.0 BOL 14239 7040 16820
L1 (×10
5
) 3.05 3.04 2.84
Table 2: Results for the network with 50 nodes.
Demands Metric ST MT 2S
D = 0.2 Φ
∗
1.38 1.34 1.90
R = 0.5 BOL 0 0 56
L1 (×10
5
) 2.10 2.11 1.91
D = 0.2 Φ
∗
2.29 1.85 5.69
R = 1.0 BOL 99 9 1166
L1 (×10
5
) 4.50 4.54 4.18
D = 0.3 Φ
∗
2.44 2.04 3.15
R = 0.5 BOL 88 30 241
L1 (×10
5
) 2.58 2.63 2.38
D = 0.3 Φ
∗
21.9 7.47 26.8
R = 1.0 BOL 11820 2862 10880
L1 (×10
5
) 5.58 5.72 5.39
4.2 Results
In Tables 1, 2 and 3 the results for the optimization
approaches are shown. In the first column, the de-
mand generation parameters (D,R) are shown. The
second column shows the metrics, while columns 3, 4
and 5 show the results of each optimization approach,
according to the metrics. Four scenarios are given
for each network: the first rows show the example
with less demands, while the last rows show the worst
case scenario. The middle rows show two intermedi-
ate scenarios, where in one case the unicast demands
are low, but the multicast demands are high and in the
next the reverse takes place.
A different perspective is shown in Figures 2, 3
and 4, where the congestion measure (Φ
∗
) for the
three networks is plotted. In each plot, the four sce-
narios in terms of demands are shown. The values are
shown in a logarithmic scale, given the exponential
nature of the penalty function.
Table 3: Results for the network with 80 nodes.
Demands Metric ST MT 2S
D = 0.2 Φ
∗
1.44 1.38 1.74
R = 0.5 BOL 0 0 7
L1 (×10
5
) 2.54 2.63 2.33
D = 0.2 Φ
∗
2.09 1.90 3.02
R = 1.0 BOL 160 77 582
L1 (×10
5
) 5.01 5.12 4.64
D = 0.3 Φ
∗
2.63 2.50 3.97
R = 0.5 BOL 227 247 821
L1 (×10
5
) 3.48 3.59 3.18
D = 0.3 Φ
∗
17.7 10.4 32.6
R = 1.0 BOL 11426 6856 15242
L1 (×10
5
) 7.25 7.49 6.90
1
10
100
1 2 3 4
Congestion Cost (Φ*)
Demand Levels
Congestion Cost Values (scenario with 30 nodes)
ST
MT
2S
MT
ST
2S
D=0.2
R=0.5
D=0.2 D=0.3
R=0.5
D=0.3
R=1.0R=1.0
Figure 2: A plot of the results for congestion measure (net-
work with 30 nodes).
4.3 Discussion
The first conclusion to draw from these results is that
2S leads to sub-optimal results, in terms of overloaded
links and network congestion (visible both in the BOL
and Φ
∗
). Both the MT and ST show better results,
being able to keep the network in an acceptable be-
haviour in most scenarios. The scenario shown in
the last rows (D = 0.2 and R = 1.0) is an extreme
case, where the demandsare quite high. Although this
would not be acceptable in a real world network, it is
useful to have an idea of how the distinct optimiza-
tion methods scale. When comparing ST and MT, the
results are quite near in the low demand scenarios.
In these cases, the gain obtained by using MT is not
impressive. The gap increases with the values of D
and R, i.e. as the problem gets harder. In practical
terms, this would mean that if the network has lots of
resources in terms of bandwidth and low demands, it
is probably not worth to pay the cost of deploying a
multi-topologyprotocol. On the other hand, using this
kind of protocol allows the network to support higher
demands with the same bandwidth resources.
Regarding the L1 values, the best alternative is
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
242

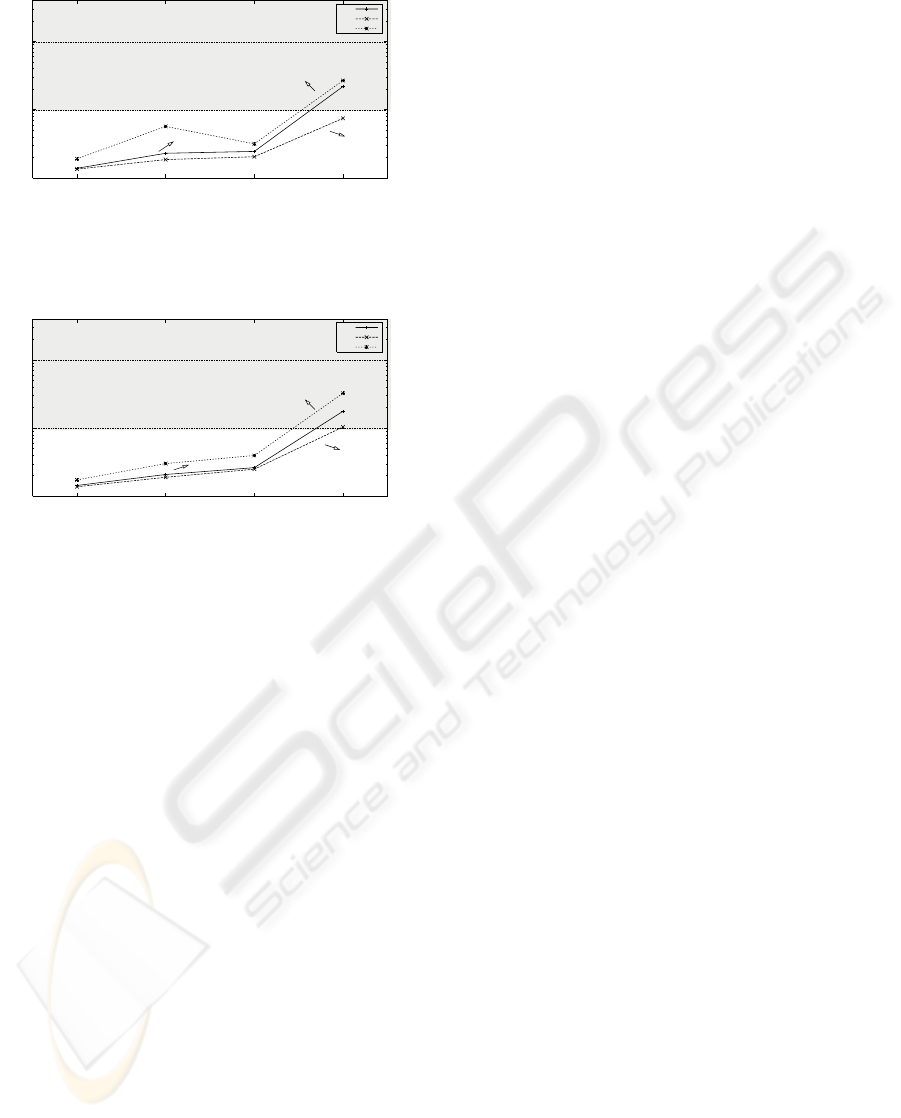
1
10
100
1 2 3 4
Congestion Cost (Φ*)
Demand Levels
Congestion Cost Values (scenario with 50 nodes)
ST
MT
2S
D=0.2
R=0.5
D=0.2 D=0.3
R=0.5
D=0.3
R=1.0R=1.0
MT
2S
ST
Figure 3: A plot of the results for congestion measure (net-
work with 50 nodes.
1
10
100
1 2 3 4
Congestion Cost (Φ*)
Demand Levels
Congestion Cost Values (scenario with 80 nodes)
ST
MT
2S
D=0.2
R=0.5
D=0.2 D=0.3
R=0.5
D=0.3
R=1.0R=1.0
2S
MT
ST
Figure 4: A plot of the results for congestion measure (net-
work with 80 nodes.
2S and thus this method allocates better the multicast
traffic. This is not surprising, since L1 is part of the
objective function in this case. However, this solu-
tion does not result in a good performance when the
network congestion is taken as a whole. So, this so-
lution would lead to high levels of loss, that would be
unacceptable in most cases.
5 CONCLUSIONS
The optimization of OSPF weights brings important
tools for traffic engineering, without demanding mod-
ifications on the basic network model. This work
presented EAs for routing optimization in networks
with unicast and multicast demands. Resorting to
a set of network configurations and unicast/ multi-
cast demands, it was shown that the proposed EAs
were able to provide OSPF weights that can lead to
good network behaviour. The proposed approach was
favourably compared to a 2-step optimization proce-
dure, proposed in previous work, that leads to sub-
optimal results in terms of network congestion and
overloaded links. The advantages of using a multi-
topology protocol in these scenarios were also studied
and it was concludedthat these are most advantageous
when the network bandwidth resources are limited.
The main contribution of this work is the capa-
bility of optimizing the OSPF weights considering all
factors involved (i.e. all types of traffic). Using the
proposed methods, the network administrator can de-
cide if a multi-topology protocol is needed or simply
use a standard implementation of OSPF. In the future,
we will proceed with the integration of further QoS
constraints in the model, with a priority on the intro-
duction of end-to-end delays.
ACKNOWLEDGEMENTS
This work was supported by the Portuguese Foun-
dation for Science and Technology under project
POSC/EIA/59899/2004, partially funded by FEDER.
REFERENCES
Ahuja, R., Magnati, T., and Orlin, J. (1993). Network
Flows. Prentice Hall.
Awduche, D. and Jabbari, B. (2002). Internet traffic engi-
neering using multi-protocol label switching (MPLS).
Computer Networks, 40:111–129.
Davie, B. and Rekhter, Y. (2000). MPLS: Multiprotocol La-
bel Switching Technology and Applications. Morgan
Kaufmann, USA.
Dijkstra, E. (1959). A note on two problems in connexion
with graphs. Numerische Mathematik, 1(269-271).
Ericsson, M., Resende, M., and Pardalos, P. (2002). A
Genetic Algorithm for the Weight Setting Problem
in OSPF Routing. J. of Combinatorial Optimization,
6:299–333.
Fortz, B. and Thorup, M. (2000). Internet Traffic Engineer-
ing by Optimizing OSPF Weights. In Proceedings of
IEEE INFOCOM, pages 519–528.
Medina, A., Lakhina, A., Matta, I., and Byers, J. (2001).
BRITE: Universal Topology Generation from a User’s
Perspective. Technical Report 2001-003.
Michalewicz, Z. (1996). Genetic Algorithms + Data Struc-
tures = Evolution Programs. Springer-Verlag, USA,
third edition.
Moy, J. (1998). OSPF, Anatomy of an Internet Routing Pro-
tocol. Addison Wesley.
Psenak, P., Mirtorabi, S., Roy, A., Nguyen, L., and Pillay-
Esnault, P.(2006). Multi-topology (mt) routing in ospf
(internet draft).
Rocha, M., Sousa, P., Rio, M., and Cortez, P. (2006). Qos
constrained internet routing with evolutionary algo-
rithms. In Proc. IEEE Conference Evolutionary Com-
putation, pages 9270–9277. IEEE Press.
Thomas II, T. (1998). OSPF Network Design Solutions.
Cisco Press.
Wang, N. and Pavlou, G. (2007). Traffic Engineered Multi-
cast Content Delivery Without MPLS Overlay. IEEE
Transactions on Multimedia, 9(3).
AN EVOLUTIONARY ALGORITHM FOR UNICAST/ MULTICAST TRAFFIC ENGINEERING
243