DYNAMIC MODELING OF A 6-DOF PARALLEL STRUCTURE

DESTINATED TO HELICOPTER FLIGHT SIMULATION

Nicolae Plitea, Adrian Pisla, Doina Pisla and Bogdan Prodan

Technical University of Cluj-Napoca, Constantin Daicoviciu 15, RO-400020 Cluj-Napoca, Romania

Keywords: 6-DOF Parallel robot, Stewart platform, Dynamics, Modeling, helicopter flight simulation.

Abstract: The dynamic analysis is the basic element of the mechanical design and control of parallel mechanisms. The

parallel robots dynamics requires a great deal of computing as regards the formulation of the generally

nonlinear equations of motion and their solution. In this paper a solution for solving the dynamical model of

a 6-DOF parallel structure destined to helicopter flight simulation is presented. The obtained dynamical

algorithms, based on the kinematical ones, offer the possibility of a complex study for this type of parallel

structure in order to evaluate the dynamic capabilities and to generate the control algorithms.

1 INTRODUCTION

Parallel robots have some advantages over serial

ones such as higher stiffness, very good precision,

high speeds and accelerations, a better weight over

payload rate. However, kinematic and dynamic

analysis of the parallel structures is much more

complicated due to the constraints and singularities

presence. Dynamic effects and their analysis are the

basis of design specifications and advanced control

of the parallel mechanical systems.

Many of the mechanics classical methods cannot

be successfully applied for parallel robots.

There are essentially four methods:

1. Newton-Euler equations with impulse and

momentum formulation or the D’Alembert

equations;

2. Lagrange equations of first kinds with so-

called Lagrange multipliers;

3. Lagrange equations of second kind with a

minimum number of system coordinates;

4. Virtual work formulation including inertia

forces.

In (Pierrot, 1990), a simplified method of

determining the dynamic model of the HEXA robot

in two steps is proposed.

(Codourey, 1991) proposes the first dynamic

model that can be used to control the parallel

DELTA robot in real time.

(Guglielmetti, 1994) presents the inverse

dynamic model for the DELTA robot in the

analytical form using the Newton’s laws.

(Honneger, 1997) suggested the use of the

dynamic equations in an adaptive control scheme for

the Hexaglide robot, in which the pursuance errors

are used on-line to correct the parameters used in

dynamic equations.

(Stamper, 1998) present a dynamical model for a

parallel structure with three degrees of freedom.

This model was also generated with the

simplications of the Codourey model.

(Tsai, 1999) present a dynamical model for a

parallel structure with three degrees of freedom,

using the virtual principle.

(Miller, 1992) presents the complete dynamic

model of the DELTA robot based on Lagrange

equations. In this case one considers that the robot

bars possess inertia moments themselves.

To solve the dynamic model, (Merlet, 2000) uses

Lagrange formulas. He has applied the direct and the

inverse dynamic model for the “left hand”, to a

prototype accomplished at INRIA based on a KPS

kinematic chain structure.

(Pisla, 2000) propose a generalized dynamic

model for parallel robots using first order Lagrange

equations on the basis of equivalent masses.

(Guégan, 2002) presents a new solution for the

dynamic model for the Orthoglide with Newton-

Euler equations.

(Itul, 2003 and 2006) present a comparative

study among various dynamical methods and

219

Plitea N., Pisla A., Pisla D. and Prodan B. (2008).

DYNAMIC MODELING OF A 6-DOF PARALLEL STRUCTURE DESTINATED TO HELICOPTER FLIGHT SIMULATION.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 219-224

DOI: 10.5220/0001503702190224

 SciTePress

different solutions for solving the dynamical model

for the guided in three points parallel robots.

Generally, in the above mentioned contributions,

the experimental identification of dynamics for the

parallel robots is restricted to simple models in

combination with adaptive control algorithms.

Flight simulators are extensively used by the

aviation industry and the military for pilot training,

disaster simulation and aircraft development. The

different types of flight simulators range from video

games up to full-size cockpit replicas mounted on

hydraulic, electric or electromechanical actuators

(Nahon, 2000), (Andreev, 2000).

Contrary to popular belief, flight simulators are

not used to train pilots how to fly aircraft. Today’s

modern simulators are used by commercial airlines

and the military alike, to familiarize flight crews in

normal and emergency operating procedures. Using

simulators, pilots are able to train for situations that

they are unable to safely do in actual aircraft. These

situations include loss of flight surfaces and

complete power loss etc. In all cases dynamics plays

a very important role for the behaviour of parallel

structures used as flight simulators.

It is widely acknowledged that the cues provided

by a good visual system offer the bulk of realism in

a flight simulator. It has also been shown that pilots

consider the provision of consistent motion cues to

add substantially to the realism of the simulation and

to be helpful in the piloting task (Reid, 1988).

Thus, motion platforms are used on modern

high-end flight simulators in order to provide motion

cues consistent with the visual, auditory and control-

feel cues to which the pilot is also subjected.

Within the motion-related subsystems, the most

consistent research effort is over the washout

subsystem which takes the motions generated by the

aircraft equations including large displacements and

filters to provide simulator motion-base commands.

These commands must provide the pilot with

realistic motion cues, while remaining within the

simulator's motion limits (Nahon, 2000).

The paper is organized as follows:

Section 2 is dedicated to the description of the

studied 6-DOF parallel structure;

Section 3 deals with the dynamic modeling using

the virtual work principle;

Section 4 presents some simulations tests on a

parallel robot;

The conclusions of this work are detailed in the

section 5.

2 DESCRIPTION OF THE 6-DOF

PARALLEL STRUCTURE

Taking into consideration the imposed requirements

for a flight simulator, which should have 6-DOF, it

was chosen the family of type Stewart-Gough

parallel structures (Figure 1).

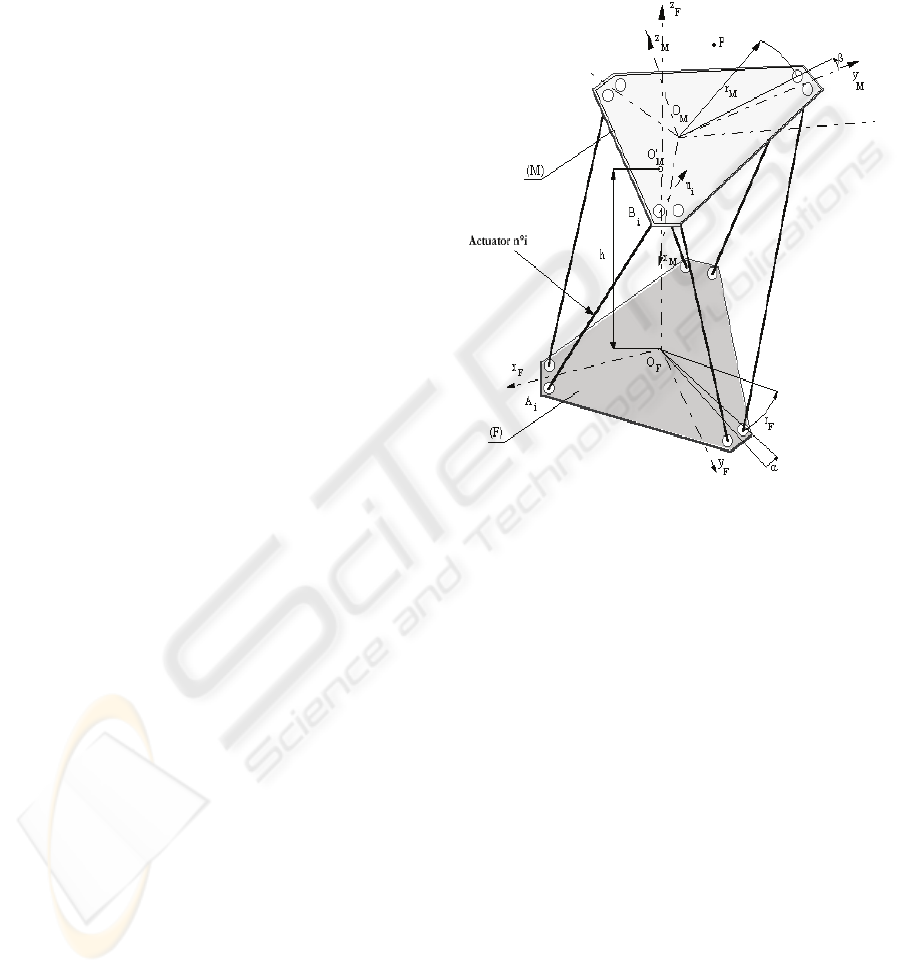
Figure 1: The 6-DOF parallel structure.

Generally, these parallel structures consist of six

mobile arms, connected to the base and mobile

platform through universal joints located at each end

of the arm.

The mobile platform materializes the end

element (end-effector). These kind of parallel

structures are characterized by a robust mechanical

structure and a high dynamic performance, a good

ratio between the manipulated mass and the own

mass.

The main difficulty results from the complexity

in the motion control. Thus, the dynamics and its

simulation is an important stage in order to test the

capabilities of the robot and to develop the adequate

control system.

2.1 Structural Considerations

For parallel mechanisms of F family the number of

degrees of mobility is calculated with formula

(Plitea, 2005):

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

220

123

C)F1(C)F2(C)F3(

C)F4(C)F5(N)F6(M

−−−−−−

−−−−−−=

(1)

where:

M - mobility degree of the mechanism; F -

mechanism family - the number of common

constraints for all mechanism elements; N - number

of mobile elements;

C - number of “i” class joints;

k = number of kinematic chains which connect the

mobile platform to the base; n - number of elements

of a kinematic chain for platform guidance for

symmetric structures;

c - number of “i” class joints

of a kinematic chain for platform guidance.

The parallel robot mechanism family is:

0F =

(2)

In our case:

;21C;6C;13N

===

(3)

The mobility degree of the parallel mechanism

will be:

C3C5N6M −−=

6M =

(4)

2.2 Kinematic Modeling

In the case of inverse geometric problem, the

actuation displacements are obtained with respect to

the position and orientation of the mobile platform.

An analytical solution could be obtained and applied

in the control algorithms. For solving the inverse

geometric problem, the transformation matrices

method was used, using the Euler angles. The model

has been already presented in (Pisla, 2007).

In the case of direct geometric problem the

position and orientation of the mobile plate is

calculated with respect to the actuation

displacements. For solving the inverse geometric

problem the transformation matrices method was

used, using the Euler angles. The solution is a

numerical one and the obtained nonlinear system

could be computed by means of Newton-

Raphson method (Pisla, 2007). The singularities

of this paralle structure have been extensively

discussed in (Pernkopf, 2002).

3 DYNAMIC MODELING OF THE

6 DOF PARALLEL ROBOT

The inverse dynamics consists in finding the

relationships between the actuating joint forces

τ ,

(i=1,2,…,6) and the motion laws for the manipulated

object.

To study the dynamics, several simplifying

hypotheses were adopted in the model:

-all joints are frictionless;

-the masses of guiding arms A

are neglected;

In Figure 2 the geometric parameters, the

corresponding system coordinates and the forces are

represented.

The used notations in the model are:

R - radius of fixed base;

e ,

d - geometric

parameters on the base;

=λ=λ ;

120=λ=λ ;

120−=λ=λ ;

r - radius of

the working platform (WP);

- geometric

parameters on the working platform;

0=δ=δ ;

120=δ=δ ;

120−=δ=δ ;

- mass of the working platform + the

helicopter;

C = mass centre for the working platform + the

helicopter; C

x’

y’

z’

- main central inertia axes;

x’

y’

z’

- main inertia moments; oxyz - coordinate

system of the mobile platform; OXYZ - fixed

reference coordinate system;

iii

ZYXO

′′′

- coordinate

system rotated with the angle

λ with respect to the

OXYZ system around the Z axis;

iii

zyxo -

coordinate system rotated with the angle

with

respect to the oxyz system around the z axis;

CXY’Z’ - mobile reference system; its axes are

parallel with the fixed coordinate system OXYZ

axes; x

, y

, z

- the coordinates of the mass centre C

with respect to the oxyz system; X

, Y

, Z

= the

coordinates of the mass centre C with respect to the

OXYZ fixed system of the robot.

In the inverse dynamic model, the input data are:

)t(),t(),t(

),t(xz),t(yy),t(xx

CCCCCC

ϕ=ϕθ=θψ=ψ

===

The actuation forces should be computed.

)t(),t(),t(

),t(),t(),t(

665544

332211

τ=ττ=ττ=τ

DYNAMIC MODELING OF A 6-DOF PARALLEL STRUCTURE DESTINATED TO HELICOPTER FLIGHT

SIMULATION

221

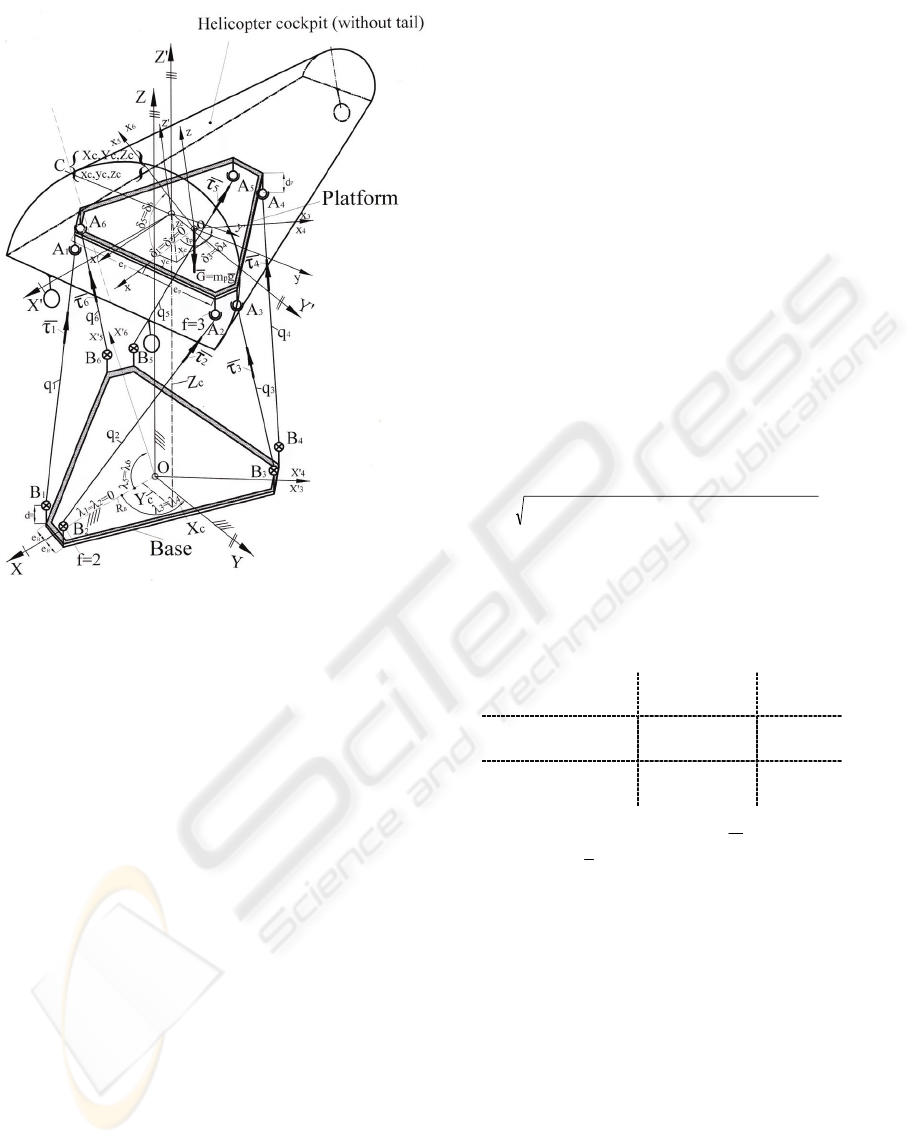
Figure 2: Dynamic modeling of the parallel robot.

The algorithm for solving the inverse dynamic

model is presented as follows.

6,....,2,1i,e)1(e

=−=

(5)

The coordinates of B

points with respect to the

iii

ZYXO

′′′

are:

6,...,2,1i,dZ,eY,RX

BBiBiBiBBi

′

(6)

The coordinates of B

points with respect to the

OXYZ are:

6,...,2,1i,

100

0CS

0SC

⎥

⎦

⎤

⎢

⎣

⎡

′

⎥

⎦

⎤

⎢

⎣

⎡

λλ

λ−λ

⎥

⎦

⎤

⎢

⎣

⎡

(7)

6,...,2,1i,e)1(e

=−=

−

(8)

6,...,2,1i

,dz,ey,rx

pAipiAipAi

−=

′

(9)

The coordinates of A

points with respect to the

iii

zyxo are:

6,...,2,1i

100

0cs

0sc

⎥

⎦

⎤

⎢

⎣

⎡

′

⎥

⎦

⎤

⎢

⎣

⎡

δδ

δ−δ

⎥

⎦

⎤

⎢

⎣

⎡

(10)

The coordinates of A

points with respect to the

OXYZ are:

6,...,2,1i

CAi

321

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

γγγ

βββ

ααα

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

(11)

Using the relations (7) and (11) the joint

coordinates are:

( )()()

6,...,2,1i

BiAiBiAiBiAi

ZZYYXX

222

++=

−−−

(12)

We consider the rotations around the

ZC,YC,XC

′′′

axes (axes parallel with the fix ones

OX, OY, OZ):

=CθCφ A

=-Sφ

= CθSφ B

= Cφ

=-Sθ C

(13)

Then, the angular speed

and the angular

acceleration

ε of the mobile platform may be

determined with the following relations:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

321

CCC

BBB

AAA

(14)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

&&&

321

CCC

BBB

AAA

CCC

BBB

AAA

(15)

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

222

For the rotations around the fix axes

ZC,YC,XC

′′′

the corresponding cosines may be

determined using the following equations:

θΨ=γθΨ=γθ−=γ

ϕθψ+ϕψ−=βϕθψ+ϕψ−=βϕθ=β

ϕθψ+ϕψ=αϕθψ+ϕψ−=αϕθ=α

cccss

ssccssssccsc

cscsscsssccc

321

(16)

The inertia moments are:

⎪

⎩

⎪

⎨

⎧

αγ−αγ−αγ−==

γβ−γβ−γβ−==

βα−βα−βα−==

γ+γ+γ=

β+β+β=

α+α+α=

′′′′

′

33z22y11xZXXZ

33z22y11xYZZY

33z22y11xXYYX

1XZ

1XY

1XX

IIIII

IIII

(17)

Then, the actuation forces

τ are obtained:

()

{}

τ=++

−

TXCXMI

&&&

(18)

where

⎥

⎦

⎤

⎢

⎣

⎡

666564636261

565554535251

464544434241

363534333231

262524232221

161514131211

CCCCCC

(19)

⎥

⎦

⎤

⎢

⎣

⎡

333231

232221

131211

aaa000

000m00

0000m0

00000m

(20)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

333231

232221

131211

bbb000

000000

(21)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

=τ

(22)

In (19)-(21):

3311

aa ,,L depend on the

platform inertia moments

XZZYYXZYX

IIIII,I

′′′′′′′′′

and

3..1iC,B,A

iii

= ;

3311

b,,b L depend on the

platform inertia moments

XZZYYXZYX

IIIII,I

′′′′′′′′′

and

3..1iC,B,A

iii

;

6611

C,,C L depend on the

direction cosines for the platform, the coordinates of

points

6..1iA

= and the coordinates of the platform

mass center

6..1iC

= .

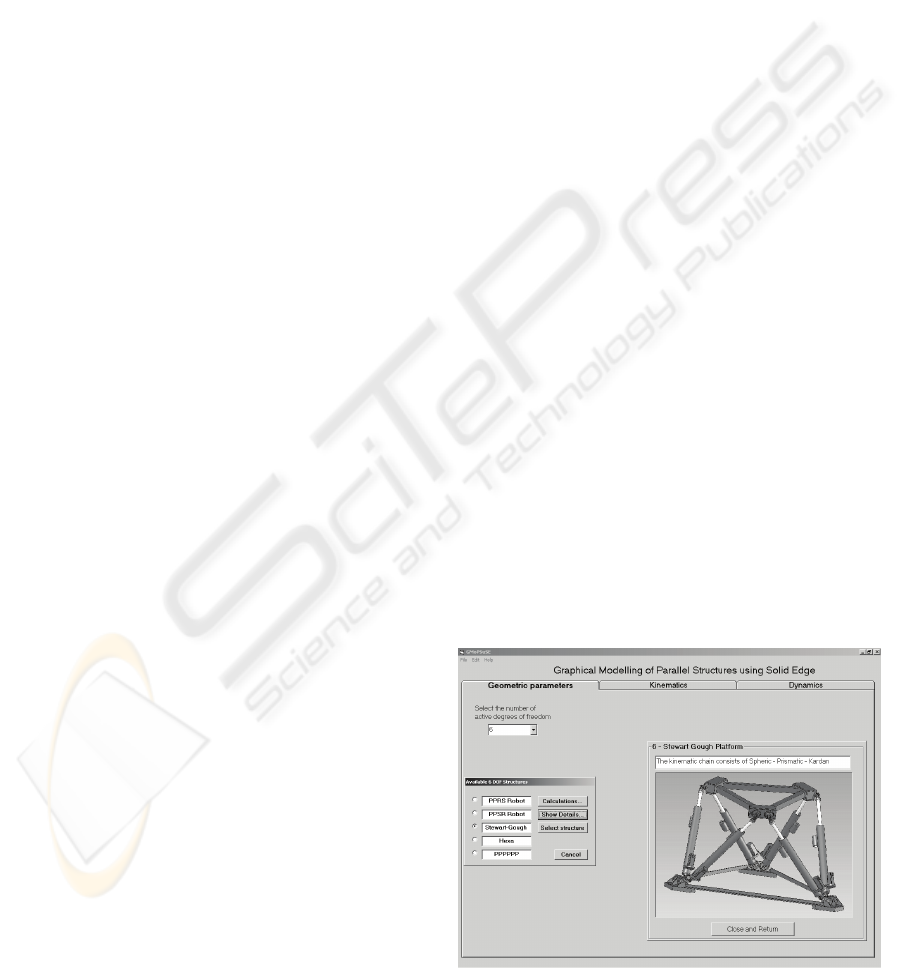
4 SIMULATION TESTS

The achieved kinematic and dynamic algorithms

have been implemented in the developed simulation

system (Pisla, 2005), (Pisla, 2007). It consists of five

main modules: Kinematics; Singularities;

Workspace; Trajectory, Dynamics. Within the

simulation system the virtual graphical model was

created, the 3D functional model allows the designer

to understand its functionality (Figure 3).

The geometric parameters can be modified

within the 3D modeling software influencing the

simulation environment. The assembly relations

between the parts, subassemblies and between parts

and subassemblies can be also modified. These

facilities enable the possibility to develop complex

relations between the shape of the workspace, links

and geometrical dimensions in order to optimize the

parallel structure.

The parallel structure parameterization enables

the development of the geometric optimization and

the robot workspace shape. The obtained results are

useful for the designers in understanding the

workspaces characteristics distribution and parallel

robots optimization.

Figure 3: Simulation program for a 6-DOF parallel

structure.

DYNAMIC MODELING OF A 6-DOF PARALLEL STRUCTURE DESTINATED TO HELICOPTER FLIGHT

SIMULATION

223

The presented simulation system enables the

motion visualization in a modular manner valid for

virtually any structure of parallel robot, introducing

the kinematic and dynamic models over the virtual

robot. The introduction of extra conditions related to

any component is possible with a relative small

number of actions. By using the graphical interface

presented in Figure 3, the facilities of the simulation

software enable to develop a complex study about

the robot kinematics and dynamics in order to

optimize the parallel structure.

5 CONCLUSIONS

In this paper a solution for solving of the inverse

dynamics for a 6-DOF parallel robot conceived for a

helicopter simulator has been presented. The

dynamic model derived through virtual work

principle has a compact form and offer the

possibility of a more complex dynamic study in

order to evaluate their dynamic capabilities and to

generate innovative control algorithms.

ACKNOWLEDGEMENTS

This research was financed from the research grants

awarded by the Romanian Ministry of Education

Research and Youth.

REFERENCES

Pierrot, F., M. Uchijama, , P. Dauchez, Fournier, A., 1990,

A New Design of a 6-DOF Parallel Robot, Journal of

Robotics and Mechatronics, 2: 92-99.

Codourey. A., 1991. Contribution a la Commande des

Robots Rapides et Precis. Application au robot

DELTA a Entrainement Direct. These a l’Ecole

Polytechnique Federale de Lausanne.

Guglielmetti, P. and Longchamp, R., 1994. A Closed

Form Inverse Dynamics Model of the DELTA Parallel

Robot. In the Symposium on Robot Control, pages 51-

56, Capri, Italia.

Stamper, R. and Tsai, L.W., 1998. Dynamic Modeling of a

Parallel Manipulator with Three Translational Degrees

of Freedom. DETC98/MECH-5956, in ASME Design

Engineering Technical Conference, Atlanta, GA.

Honneger, M. Codourey, A. and Burdet, 1997. E.

Adaptive control of the Hexaglide, a six d.o.f. parallel

manipulator. In IEEE Int. Conf. On Robotics and

Automation, pages 543-548, Albuquerque.

Tsai, L.-W., 1999. Robot Analysis, the Mechanics of

Serial and Parallel Manipulators, Wiley.

Guégan, S. and Khalil. W., 2002. Dynamic Modeling of

the Orthoglide. Advances in Robot Kinematics

(J.Lenarcic and F. Thomas, Ed.). Kluver Academic,

Publication, Netherlands, 387-396.

Geng Z..and Haynes, L.S., 1992. On the dynamic model

and kinematic analysis of a class of Stewart platforms.

Robotics and Autonomous Systems, 9:237-254.

Liu, K., 1993. The singularities and dynamics of a Stewart

platform manipulator. Journal of Intelligent and

Robotic Systems, 287-308.

Miller, K. and Clavel. R., 1992. The Lagrange-Based

Model of DELTA-4 Robot Dynamics. Robotersysteme,

8:49-54.

Merlet. J.-P., 2000. Parallel robots. Kluver Academic

Publisher.

Pisla, D., Kerle, H., 2000. Development of Dynamic

Models for Parallel Robots with Equivalent Lumped

Masses. In 6th International Conference on Methods

and Models in Automation and Robotics, , pages 637-

642, Międzydroje, Poland.

Itul, T. and Pisla, D., 2003. Comparative Study between

D’Alembert Principle and Lagrange Formulation for

Guiding in three Points Parallel Robot Dynamic

Analysis. In 14th International Conference on Control

Systems and Computer Science, Politehnica Press,

Bucharest, 1:100-105.

Itul, T., Pisla, D. and Pisla, A., 2006.

On the Solution of

Inverse Dynamics for 6-DOF Robot with Triangular

Platform, in 1st European Conference on Mechanism

Science, E

UCOMES, ISBN 3-901249-85-0 (on CD),

Obergurgl, Austria, February 21–26.

Kovecses, J., Piedboeuf and J.C., Lange, C., 2002.

Methods for Dynamic Models of Parallel Robots and

Mechanisms, in the Workshop on Fundamental Issues

and Future Research Directions for Parallel

Mechanisms and Manipulators, pages 339-347,

Quebec.

Reid L.D., Nahon M.A., 1988. Response of Airline Pilots

to Variations in Flight Simulator Motion Algorithms,

Vol. 25, No. 7, 639-646.

Nahon M.A., Gosseli, 2000. A comparison of flight

simulator motion – base architectures, Journal of

Mechanical Design, Volume 122.

Andreev A. N., Danilov A. M.. Information models for

designing, conceptual broad-profile flight simulators,

Measurement Techniques, Vol 43, No. 8.

Plitea, N., Hesselbach, J., Pisla, D., Raatz, A., Vaida, C.,

Wrege, J., Burisch, A., 2006. Innovative Development

Of Parallel Robots And Microrobots, Acta Tehnica

Napocensis, Series of Applied Mathematics and

Mecanics, no. 49, vol. 5, pp. 15-26.

Pisla, A., Plitea, N., Prodan, B., 2007. Modeling and

simulation of parallel structures used as flight

simulators, in Proc of TMT2007, Tunisia.

Pernkopf, F., Husty, M.L., 2002. Singularity analysis of

spatial Stewart-Gough platforms with planar base and

platform, In Proc. ASME Design Eng. Tech. Conf.

Montreal, Canada, September 30 October 2.

Pisla, D. L, 2005. Modelarea cinematica si dinamica a

robotilor paraleli, Editura Dacia Cluj-Napoca.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

224