FREQUENCY CONTROL FOR ULTRASONIC PIEZOELECTRIC

TRANSDUCERS, BASED ON THE MOVEMENT CURRENT

Constantin Voloşencu

Automatics and Applied Informatics Department, “Politehnica” University of Timisoara

Bd. V. Parvan nr. 2, 300223 Timisoara, Romania

Keywords: Control systems, Piezoelectric transducers, Frequency control, High power ultrasonics.

Abstract: This paper provides a method for frequency control at the ultrasonic high power piezoelectric transducers,

using a feedback control systems based on the first derivative of the movement current. This method assures

a higher efficiency of the energy conversion and greater frequency stability. A simulation for two kinds of

transducer model is made. The method is implanted on a power electronic generator. Some transient

characteristics are presented.

1 INTRODUCTION

Piezoelectric transducers (Gallego-Juarez, 1989)

have proved their huge viability in the high power

ultrasonic applications as cleaning, welding,

chemical or biological activations and other for

many years (Hulst, 1972), (Neppiras, 1972). And

these applications continue to be of a large necessity.

The power ultrasonic transducers are fed with

power inverters, using transistors working in

commutation at high frequency (Bose, 1992). A

large scale of electronic equipments, based on

analogue or digital technology, is used for control in

the practical applications (Marchesoni, 1992.).

A good efficiency of the energy conversion in

the power ultrasonic equipments is very important to

be assured. Different control methods are used in

practice to control the signal frequency in the power

inverters (Ramos, et. all., 1985), (Fabianski and

Palczynski, 1989).

The high power ultrasonic piezoelectric

transducers are analysed with complex structures by

using equivalent circuits (Lazaro et. all. 1989),

starting from Mason's model, implemented on circuit

analysis programs (Morris, 1986).

Many frequency control methods, structures and

devices, on this field of interest, are patented.

This paper presents a method to control the

frequency of the feeding voltage for the piezoelectric

transducer. A power amplifier working in

commutation at high frequency generates the

feeding voltage. The control system is based on a PI

controller, which keep at zero the derivative of the

movement current. This control assures the

maximum of the mechanic power generated by the

transducer.

2 RELATED WORK

To perform an effective function of an ultrasonic

device for intensification of different technological

processes a generator should have a system for an

automatic frequency searching and tuning in terms

of changes of the oscillation system resonance

frequency. The article (Khmelev, et all., 2001)

presents a system of phase-locked-loop frequency

control of ultrasonic generators with automatic

resonance frequency searching in the given band of

frequencies.

In (Furuichi and Nose, 1981) a driving circuit for

ultrasonic tools which uses a piezoelectric

transducer to convert ultrasonic electric signals into

ultrasonic mechanical vibrations includes a voltage-

controlled oscillator which produces an output signal

at a frequency that is proportional to an input

voltage, a power amplifier stage having its input

coupled to the output of the voltage-controlled

oscillator.

In (Hasegawa, 2003) an automatic frequency

control (AFC) circuit is based on a frequency offset

estimating circuit produces a lock signal if a

calculated frequency error becomes smaller than a

predetermined value.

194

Volo¸sencu C. (2008).

FREQUENCY CONTROL FOR ULTRASONIC PIEZOELECTRIC TRANSDUCERS, BASED ON THE MOVEMENT CURRENT.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 194-199

DOI: 10.5220/0001503801940199

 SciTePress

The dynamic characteristics of a fixed measuring

transducer are defined not only by the parameters of

its mechanical system and the ability to convert

mechanical into electrical energy but also by the

properties of the object on which the transducer is

mounted and by the mounting rigidity. In the paper

(Senchenkov, 1991) the block diagram is discussed

of a system that will detect and evaluate the faults in

measuring transducers by comparing the amplitude-

frequency characteristic obtained by applying

electric pulses to the piezoelement of the transducer

with the amplitude-frequency characteristics

obtained for the transducer in its natural state and at

the moment after it has been mounted on an object.

In (Sullivan, 1983) a power supply is provided

for an electromechanical device of the type

employing ultrasonic frequency vibratory energy for

bonding materials. An automatic frequency control

varies the output frequency of the power supply until

the ratio of the maximum to minimum amplitudes of

a standing wave produced in the mechanical

vibratory member falls below a pre-set maximum.

The power supply frequency is automatically varied

to maintain the standing wave ratio below a pre-set

value which is deemed to be an acceptable value for

efficient transfer of power.

3 CONTROL PRINCIPLE

3.1 The Equivalent Circuit of the

Piezoelectric Transducer

The electrical energy of ultrasonic frequency in the

bandwidth of 20-80 kHz is converted in mechanical

energy using piezoelectric transducers. A kind of

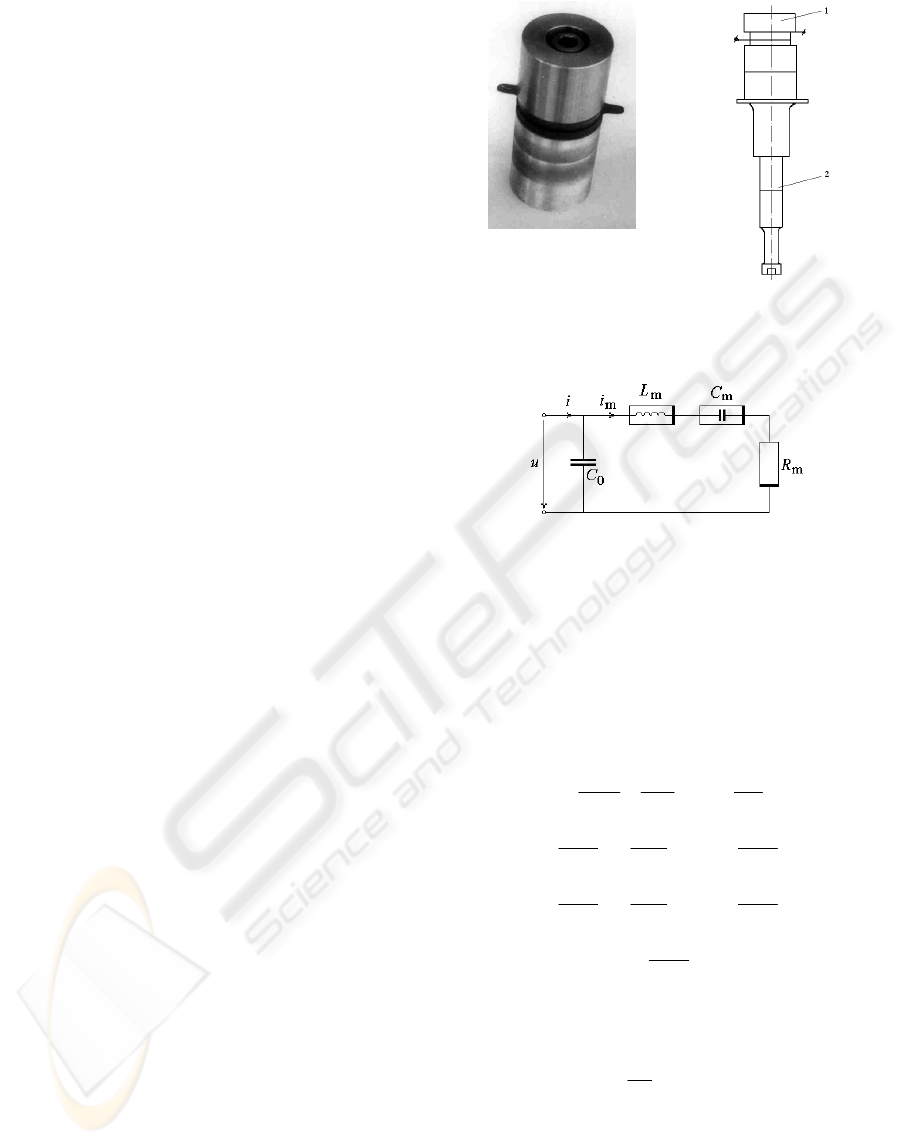
piezoelectric transducer of 100 W is presented in

figure 1,a. In practice the transducer (1) is

mechanical coupled with an energy concentrator (2),

as is presented in figure 1,b).

The ultrasonic piezoelectric transducers have the

equivalent electric circuit from figure 2. In this

circuit there is emphasized the mechanical part, seen

as a series RLC circuit, with the equivalent

parameters R

, L

and C

, which are nonlinear,

depending on the transducer load.

Figure 1 a): A piezoelectric

transducer.

Figure 1 b): Piezoelectric

transducer coupled with an

energy concentrator.

Figure 2: The equivalent circuit of the piezoelectric

transducer.

The current through the mechanical part i

is the

movement current. The input capacitor C

of the

transducer is consider as a constant parameter.

The equations (1) are describing the time

variation of the signals and the mechanical

parameters.

mLm

mCm

+===

mCm

+===

R =

iii

RmCmLm

uuuu +

00 C

C =

(1)

where ϕ is the magnetic flux through the mechanical

inductance

and q is the electric load over the

mechanical capacitor C

The piezoelectric traducer has a frequency

characteristic of its impedance

Z with a series and a

parallel resonance, as it is presented in figure 3.

FREQUENCY CONTROL FOR ULTRASONIC PIEZOELECTRIC TRANSDUCERS, BASED ON THE MOVEMENT

CURRENT

195

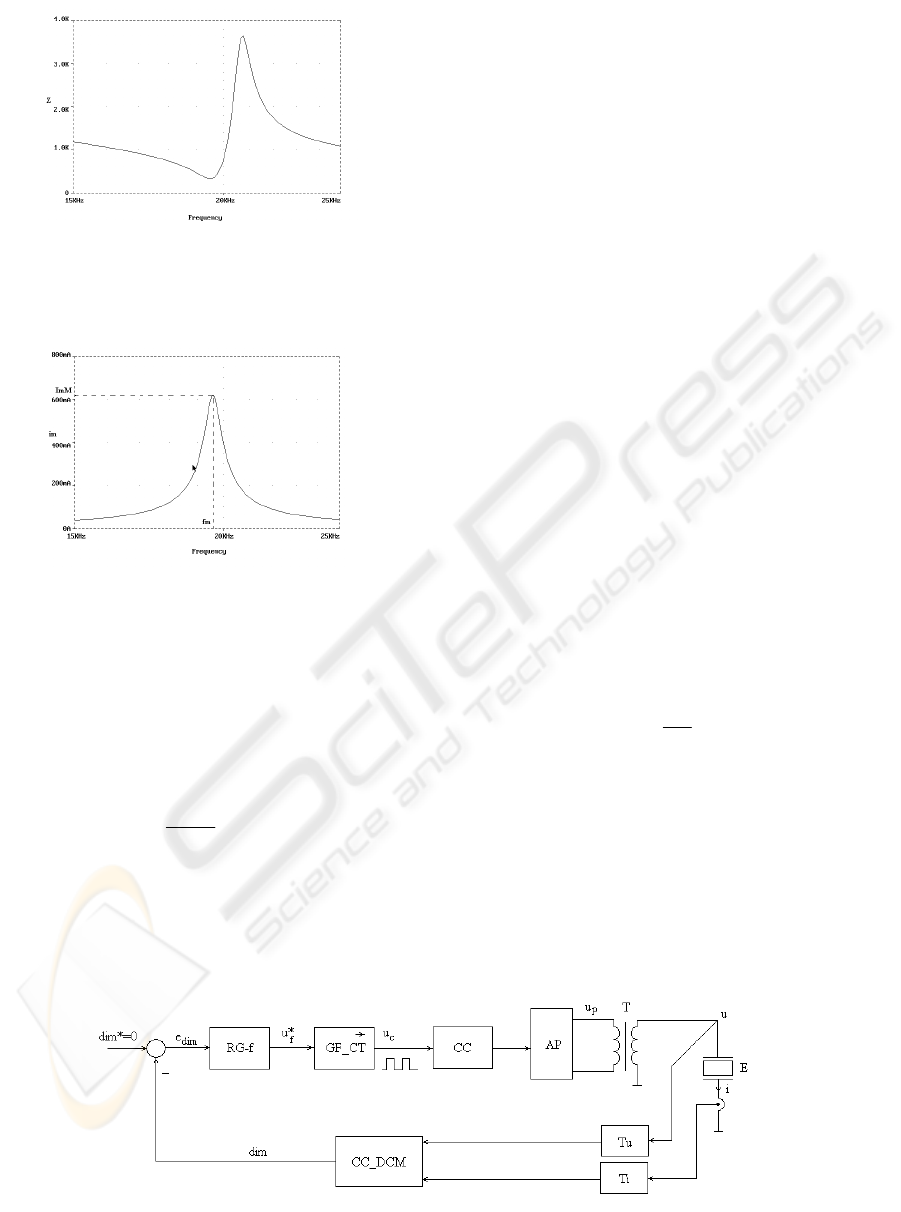
Figure 3: The frequency characteristic of the transducer

impedance.

The movement current i

has the frequency

characteristics from figure 4.

Figure 4: The frequency characteristic of the transducer

impedance.

The maximum mechanical power developed by

the transducer is obtained when it is fed at the

frequency

, were the maximum movement current

is obtained. Of course, the maximum of the

movement current i

is obtained when the derivative

of the absolute value of the movement current

dim is

zero:

)dim( ==

(2)

So, a frequency control system, functioning after

the error of the derivative movement current may be

developed, is using a PI frequency controller, to

assure a zero value for this error in the permanent

regime.

3.2 The Frequency Control System

The block diagram of the frequency control system

based on the above assumption is presented in figure

A power amplifier AP, working in commutation,

at high frequencies, feeds a piezoelectric transducer

E, with a rectangular high voltage

u, with the

frequency f. An output transformer T assures the

high voltage

u for the ultrasonic transducer E. A

command circuit CC assures the needed command

signals for the power amplifier AP. The command

signal

is a rectangular signal, generated by a

voltage controlled frequency generator GF_CT. The

rectangular command signal

has the frequency f

and equal durations of the pulses. The frequency of

the signal

is controlled with the voltage u

*. The

signal u

* to control the frequency f of the transducer

is provided by the frequency controller RG-f.

The frequency control system from figure 4 is

based on the derivative movement current error

dim

dimdim

dim

−=e

(3)

as the difference between the reference value

dim*=0 and the computed value of the derivative

dim.

A PI controller is used to control the frequency,

with the following transfer function:

)(

1)(

dim

Ksu

⎟

⎠

⎞

⎜

⎝

⎛

(4)

The frequency controller is working after the

error of the derivative of the movement current

dim

Figure 5: The block diagram of the frequency control system.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

196

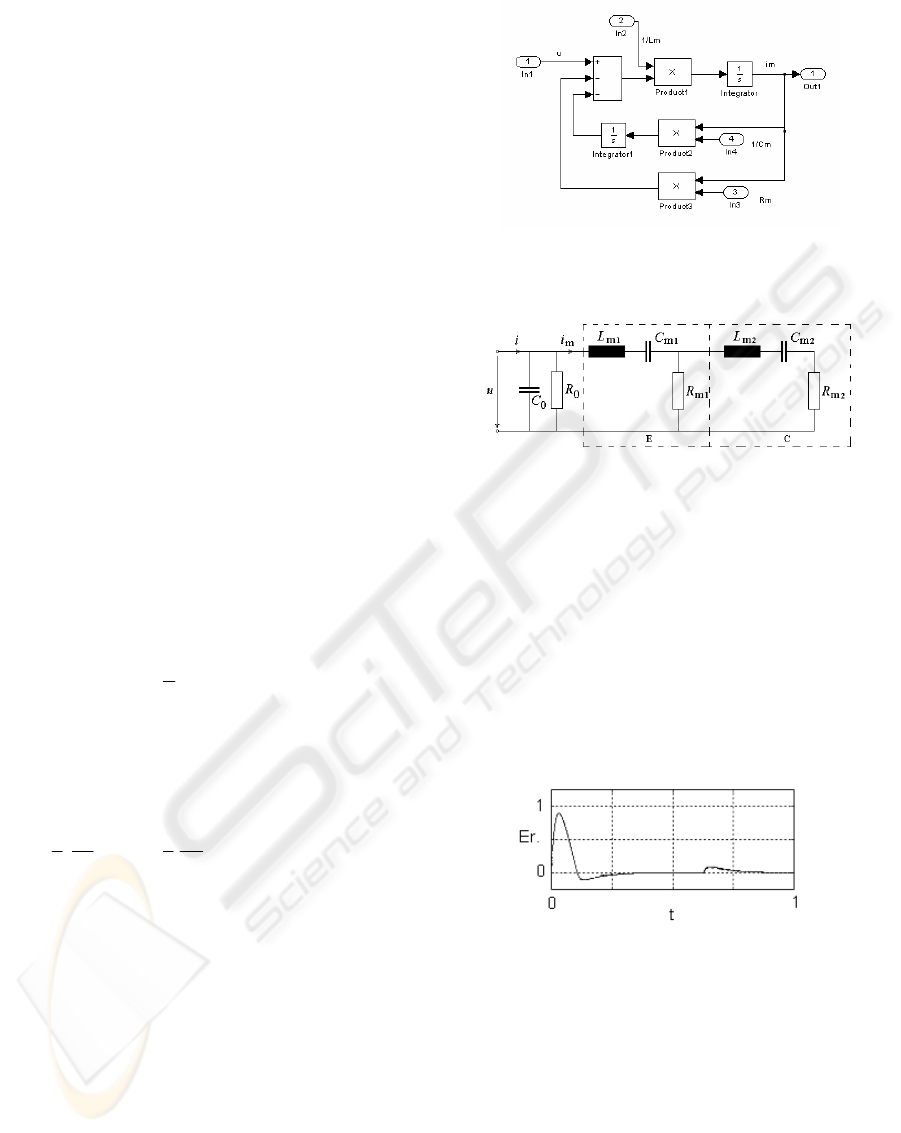
The derivative of the movement current dim is

computed using a circuit CC_DCM, where C

is the

known constant value of the capacitor from

transducer input and

u and i are the measured values

of the transducer voltage and current.

The voltage upon the transducer

u and the

current i through the transducer are measured using

a voltage sensor Tu and respectively a current sensor

Ti.

4 MODELING AND SIMULATION

Some models for different parts of the block

diagram from figure 5 were developed to test the

control principle by simulation.

Two models are tested for the transducer. In the

first model the parameters of the mechanical part are

considered with a static value and a dynamical

variation. In the second model the electromechanical

transducer is considered coupled with a mechanical

concentrator.

Approximating the relations (1), the following

relations are used to model the behaviour of the

piezoelectric transducer:

)()()()()( sissLsissLsu

mmmmLm

)()()()()( ssussCsussCsi

CmmCmmCm

)]([

)( ssiR

mmRm

)()()()( susususu

RmCmLm

++=

(5)

The movement current i

(s) is modelled, based on

the above relations, with the following relation:

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

×−×−×= )()(

)(

)( siRsi

mmm

(6)

The block diagram of the movement current

model is presented in figure 6.

The mechanic parameters from the above

relations have the variations given by relations (7),

in the vicinity of the stationary points R

, L

and

mmm

CCC

LLL

RRR

Δ+=

(7)

A second model is taken in consideration. The

transducer is considered coupled with the

concentrator and the equivalent circuit is presented

in figure 7.

Figure 6: The block diagram, model for the mechanical

part of the piezoelectric transducer.

Figure 7: Equivalent circuit of the transducer with

concentrator.

In this model there is a series RLC with the

parameters L

, C

and R

for the transducer T

and a series RLC circuit with the parameters L

and R

for the concentrator C, coupled in

cascade.

The parts of the control block diagram are

modelled using Simulink blocks. A transient

characteristic of the frequency error e

dim

from the

control system is presented in figure 8.

Figure 8: Transient characteristic for the frequency control

system, obtained by simulation.

The simulation is made considering for the first

model the variation with 10 % at the transducer

parameters. The deviation in frequency is eliminated

fast. The frequency response has a small overshoot.

FREQUENCY CONTROL FOR ULTRASONIC PIEZOELECTRIC TRANSDUCERS, BASED ON THE MOVEMENT

CURRENT

197

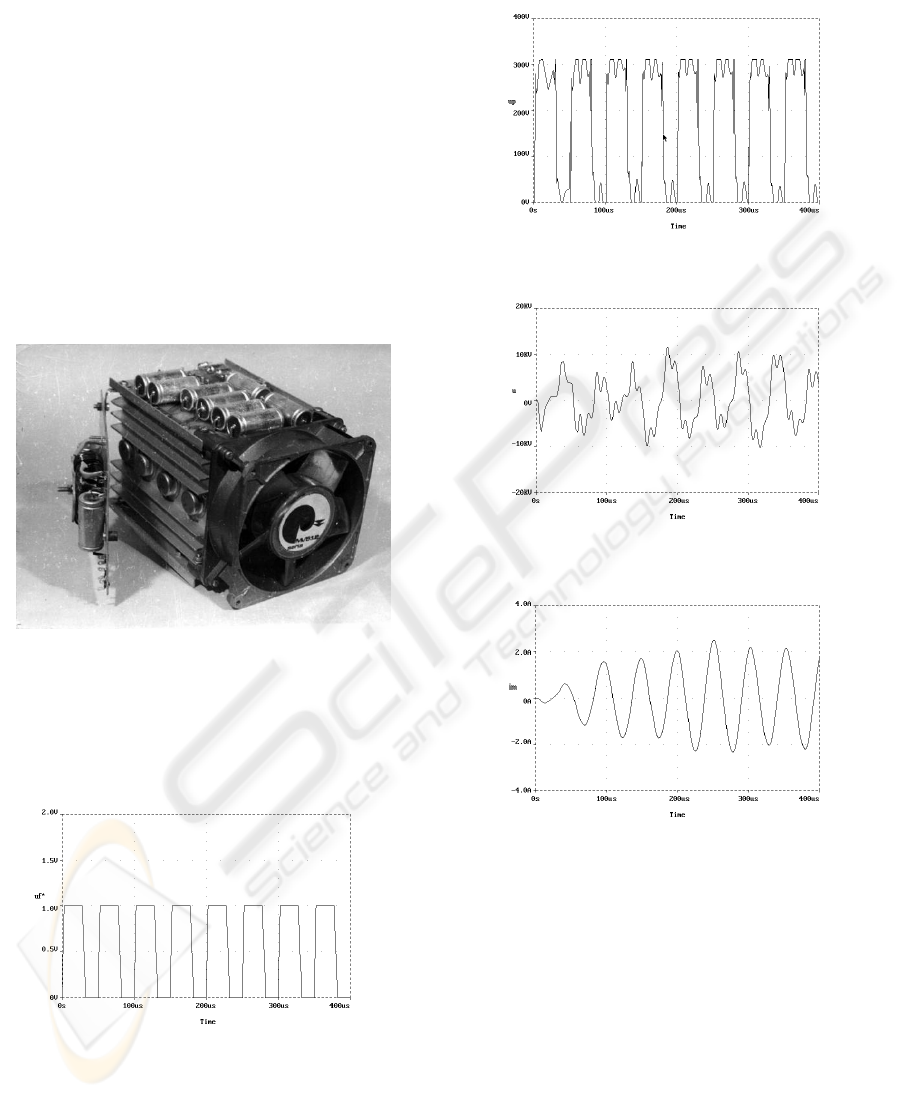
5 IMPLEMENTATION AND TEST

RESULTS

The frequency control system is developed to be

implemented using analog, high and low power,

circuits, for general usage. The power amplifier AP

is realized using four power MOSFET transistors, in

a full bridge, working in commutation at high

frequency. The voltage controlled frequency

generator GF_CT is realized using a phase lock loop

PLL circuit and a comparator. The computing circuit

CC_DCM, which implements the relations and the

frequency controller RG-f are realized using

analogue operational amplifiers. The transformer T

is realized using ferrite cores.

The electronic generator is presented in figure 9.

Figure 9: The electronic generator.

In the following figures some transient signal

variations of the control system are presented.

The pulse train of the command voltage u

presented in figure 10.

Figure 10: Examples of sensor impulse trains.

The output voltage of the power amplifier is

presented in figure 11.

The voltage u over the piezoelectric transducer is

presented in figure 12.

The measured movement current i

is presented

in figure 13.

Figure 11: The output voltage.

Figure 12: The transducer voltage.

Figure 13: The movement current.

6 CONCLUSIONS

In this paper a method to control the frequency of

the piezoelectric ultrasonic transducers based on the

movement current through the mechanical part of

the equivalent circuit of the transducer is presented.

The principle of this method is to assure the

maximum mechanical power developed by the

transducer, based on the measured transducer’s

voltage and current, controlling the feeding voltage

frequency, as the derivative of the movement current

to be zero.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

198

The frequency control system was modelled and

simulated using Matlab and Simulink. Two models

for the mechanical part of the transducer are chosen.

Two different regimes for the time variations of the

mechanical parameters of the transducer was chosen

and tested. A Simulink model and a simulation result

are presented. The simulation results have proven

that the control principle developed in this paper

gives good quality criteria for the output frequency

control.

The control system is implemented using a

power inverter with transistors working in

commutation at high frequencies and analogue

circuits for command. Transient characteristics of

the control systems are presented.

The frequency control system may be developed

for piezoelectric transducers in a large scale of

constructive types, powers and frequencies, using

general usage analogue components, at a low price,

with good control criteria.

REFERENCES

Bose, B.K., 1992. Evaluation of Modern Power

Semiconductor Devices and Future Trends of

Converters, In IEEE Trans. on Industry Applications,

march/april, vol.28, no. 2.

Gallego-Juarez, J.A., 1989. Piezoelectric Ceramics and

Ultrasonic Transducers, In J. Phys. Sci. Instrum. (U.K.),

oct., vol. 22, no. 10.

Hulst, A.P., 1972. Macrosonics in industry 2. Ultrasonic

welding of metals, In Ultrasonics, Nov.

Fabianski, P., Palczynski, L., 1989. Power Inverter with

Self-Tuning Output Frequency for Ultrasonic Cleaning

System, In EPE'89, 3-rd European Conference on

Power Electronics and Applications, Aachen,

Germany, oct.

Khmelev, V.N., Barsukov, R.V., Barsukov, V., Slivin,

A.N., Tchyganok, S.N., 2001. System of phase-

locked-loop frequency control of ultrasonic generators,

In Electron Devices and Materials, 2001.

Proceedings. 2nd Annual Siberian Russian Student

Workshop on.

Lazaro, O.J.C., San Sanche, P.T., Gallego-Juarez, J.A.,

1989. Analysis of an ultrasonic transducer with

complex structure by using equivalent circuits, In

Ultrasonics International, Conference Proceedings,

Madrid, Spain.

Marchesoni, M., 1992. High-Performance Current Control

Techniques for Applications to Multilevel High-Power

Voltage Source Inverters, In IEEE Trans. on Power

Electronics, Jan.

Morris, A.S., 1986. Implementation of Mason's model on

circuit analysis programs, In IEEE Transactions on

ultrasonics, ferroelectric and frequency control, vol.

UFFC-33, no. 3.

Mori, E., 1989. High Power Ultrasonic Wave Transmission

System, In J. Inst. Electron. Inf. Commun. Eng., vol. 72,

no. 4, April.

Neppiras, E.A., 1972. Macrosonics in industry, 1.

Introduction. In Ultrasonics, Jan.

Ramos, F.A., Montoya, V.F., Gallego-Juarez, J.A., 1985.

Automatic system for dynamic control of resonance in

high power and high Q ultrasonic transducers, In

Ultrasonics, July.

I. K.Senchenkov, I.K., 1991. Resonance vibrations of an

electromechanical rod system with automatic

frequency control, In International Applied

Mechanics, Vol. 27, No. 9/ Sept., Springer, N. Y.

Furuichi, S., Nose, T., 1981. Driving system for an

ultrasonic piezoelectric transducer, U.S. patent

4271371.

Hasegawa, O., 2003. Automatic frequency control circuit,

U. S. Patent 6571088.

Sullivan, R.A., 1983. Power supply having automatic

frequency control for ultrasonic bonding, U. S. Patent

4389601.

FREQUENCY CONTROL FOR ULTRASONIC PIEZOELECTRIC TRANSDUCERS, BASED ON THE MOVEMENT

CURRENT

199