SLIDING

MODE CONTROL

Is it Necessary Sliding Motion?

L. Acho

Department of Applied Mathematics III, EUETIB-Universidad Polit

ecnica de Catalu

Comte d’Urgell 187, 08036-Barcelona, Spain

Keywords:

Sliding Mode Control.

Abstract:

Sliding mode control has been recognized to be insensitive to exogenous perturbations if the reachability

conditions is warranted. Two phases follow the dynamics of the closed-loop perturbed system: 1) Finite-time

convergence to the sliding surface, and 2) Sliding motion along the sliding surface. In the sliding motion the

system has a reduced-order dynamic behavior. But, is it really necessary to have sliding motion to warranty

the robustness property of the sliding mode controller? The main objective of this position paper is to theorize

this important question.

1 INTRODUCTION

The most distinguished feature of sliding mode con-

trol it its ability to issue very robust control systems

facing exogenous perturbations. Moreover, sliding

mode control has been applied to a wide variety of

control objectives such as regulation, tracking con-

trol, model following, adaptive control, observer de-

sign, among others (Perruqueti and Barbot, 2002; Ed-

wards and Spurgeon, 1998). However, in all issues,

sliding motion is secure to keep operable the sliding

mode controller. Basically, the sliding controller in-

volves two steps design. Ones is the ﬁnite-time con-

vergence to the discontinuity manifold (the sliding

surface), and the second one is the design of the slid-

ing dynamics. However, and according with the ex-

amples given here, sliding motion is not necessary to

warranty the main property of sliding controllers: in-

sensitiveness to external perturbations. The outline of

this position paper is as follows. The basic idea of

sliding mode control using a second-order system is

studied in Section two. Section three, two examples

where not sliding motion exits all the time are granted

and applied to a perturbed system illustrating that the

insensitiveness property is not loss. Finally, Section

ﬁve the conclusions are stated.

2 SLIDING MODE CONTROL

The basic idea of sliding mode control can be il-

lustrated using second-order system (J. Y. Hung and

HUng, 1993; Edwards and Spurgeon, 1998; Perru-

queti and Barbot, 2002). At this point, consider the

following system (Perruqueti and Barbot, 2002):

˙x

= x

˙x

= −x

+ u. (1)

This system represents a dc-motor model, where u is

the scalar input control. Let us assume that the sliding

surface is speciﬁed as:

s(x

) = x

+ αx

= 0, α > 0. (2)

The control objective consists to ﬁnd a control law u

such that the sliding surface is attractive and reachable

in ﬁnite time. In the sliding surface, the sliding mode

motion then takes place (Perruqueti and Barbot, 2002;

Edwards and Spurgeon, 1998; J. Y. Hung and HUng,

1993). The reachability in ﬁnite time is warranted if

s ˙s ≤ η|s|, η > 0, (3)

called the η−reachability condition (Edwards and

Spurgeon, 1998; Perruqueti and Barbot, 2002). Then,

from (2), we have

s ˙s = s( ˙x

+ α ˙x

). (4)

Invoking (1), we get

275

Acho L. (2008).

SLIDING MODE CONTROL - Is it Necessary Sliding Motion?.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 275-277

DOI: 10.5220/0001504202750277

 SciTePress

s ˙s = s(−x

+ u + αx

)

= s((α − 1)x

+ u). (5)

If we set

u = −(α − 1)x

− ηsgn(s), η > 0, (6)

we arrive to

s ˙s = s(−ηsgn(s)) = −η|s|. (7)

So, any trajectory of the closed-loop system (1) and

(6), reaches the sliding surface s = 0 in ﬁnite time.

Furthermore, in the sliding surface, the dynamic mo-

tion yields:

+ αx

= ˙x

+ αx

= 0 ⇒ ˙x

= −αx

(8)

which is asymptotically stable because α > 0. Ob-

serve that the trajectory in the sliding surface can not

scape from it. In resume, slide mode control involves

two steps. Design a control law such as the sliding

manifold be attractive and reachable in ﬁnite time,

and design the sliding mode dynamics such as it is

asymptotically stable. Also, it is recognizable that in

sliding motion the order of the system is reduced from

two to one. Let us now assume exogenous perturba-

tion in our system. So, let it be as:

˙x

= x

˙x

= −x

+ u + sin(t) (9)

where the exogenous perturbation is bounded. Then,

using (6), we have:

s ˙s = −η|s| + sin(t)s ≤ −η|s| + |s| = −|s|(η − 1).

(10)

So, the η-reachability condition is satisﬁed with η > 1

and any trajectory of the closed-loop perturbed sys-

tem (9) and (6) reaches the sliding surface in ﬁnite

time, where its sliding mode dynamics ( ˙x

= −αx

)

is unaltered in spite of the external perturbation. Sim-

ulations results are given in Fig. 1 with α = 0.5 and

η = 2.

3 MODIFIED SLIDING MODE

CONTROL

Here, our main contributions are stated. The objec-

tive is to eliminate the persistency of chattering in

the control law keeping the beneﬁts of the sliding

0 2 4 6 8 10

−0.5

0.5

Time(sec.)

0 0.5 1

−0.8

−0.6

−0.4

−0.2

0.2

0 2 4 6 8 10

−3

−2

−1

Time(sec.)

Control law

sliding

surface

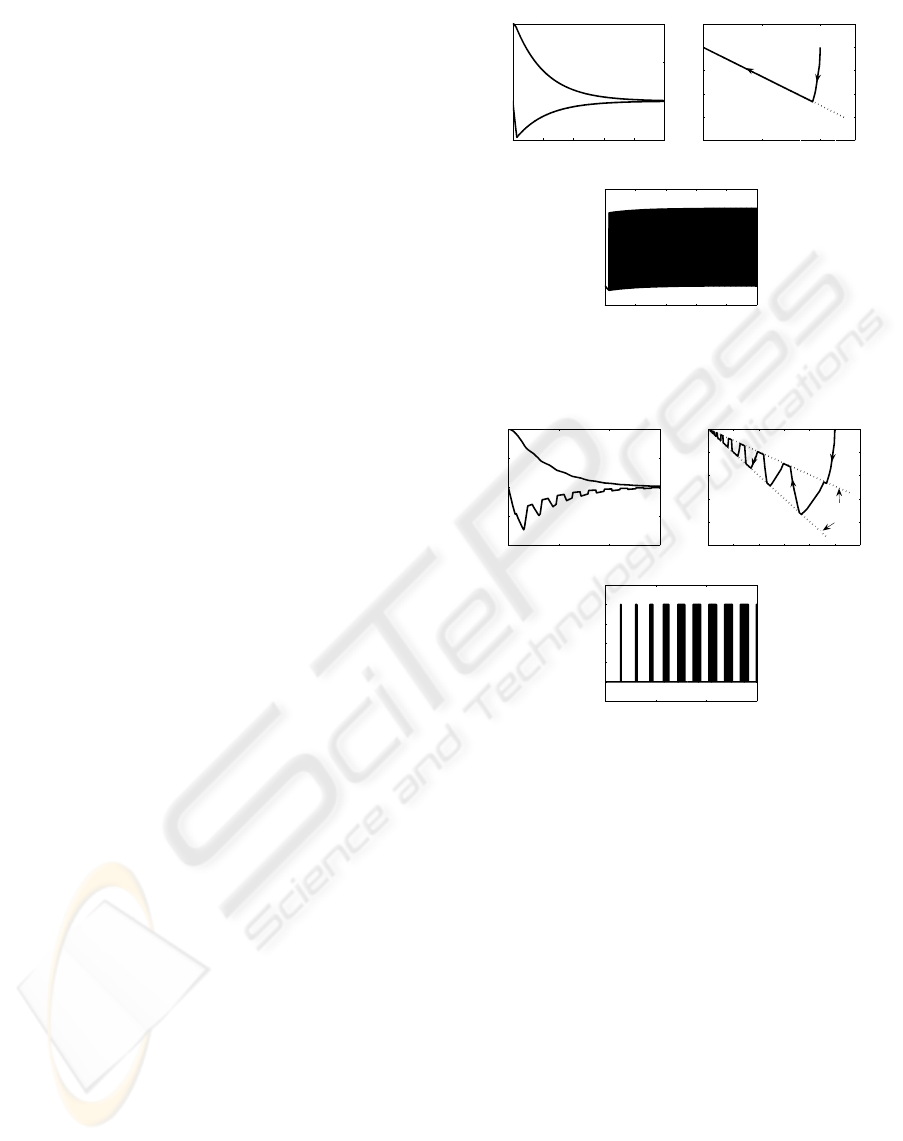
Figure 1: Simulations results of the perturbed system with

(0) = 1 and x

(0) = 0.

0 2 4 6

−1

−0.5

0.5

Time(sec.)

0 0.2 0.4 0.6 0.8 1

−1

−0.8

−0.6

−0.4

−0.2

0 2 4 6

−3

−2

−1

Time(sec.)

Control law

sliding

surfaces

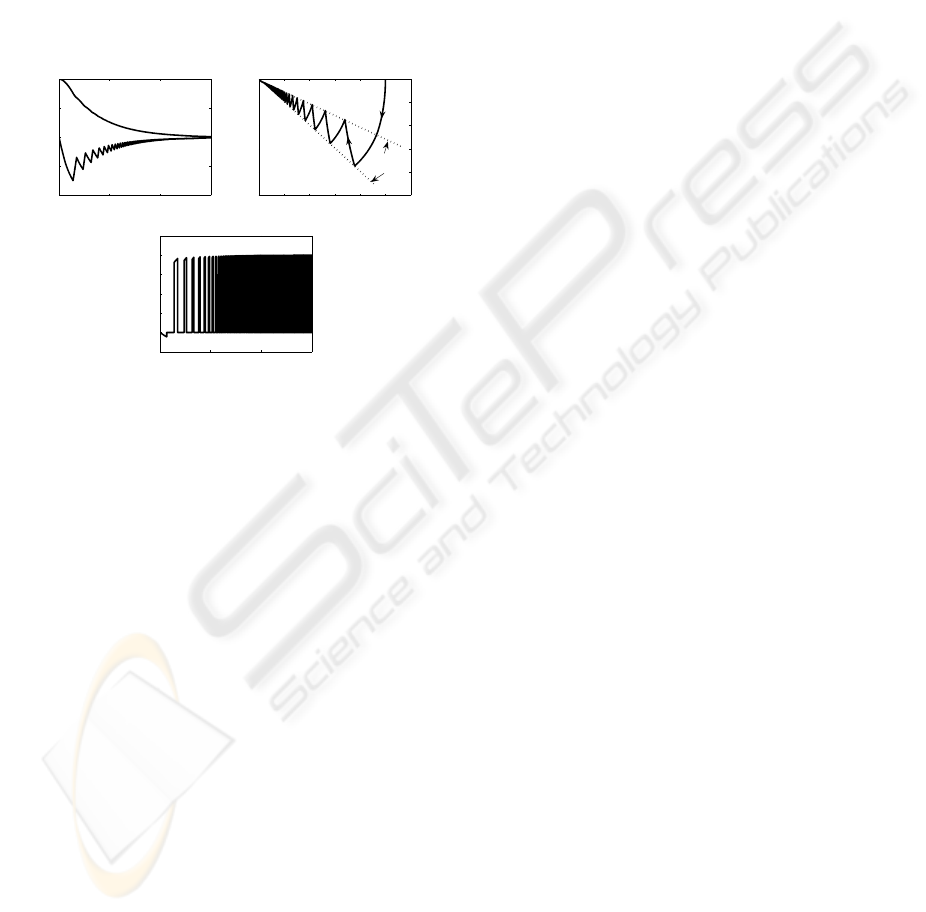
Figure 2: Simulations results of the perturbed system with

(0) = 1 and x

(0) = 0 utilizing the modiﬁed sliding mode

control.

mode control. From Fig. 1, when the system is per-

turbed and the η-reachability conditions is satisﬁed,

the closed-loop system is insensitive to external per-

turbations, but chattering is sustained almost all the

time. One way to reduce persistency on chattering

is by means of changing the value of α in (6) and

(2). For instance, employing the same perturbed sys-

tem (9), with η = 2, and the same initial conditions;

changing α from 0.5 to 1 at a frequency of 5/πHz (a

square signal), the simulation results are shown in Fig.

2. Here, the property of insensitiveness to external

perturbations is evident and the chattering persistency

is reduced. The commutation in the value of α is sim-

ilar to commuting between two sliding surfaces (see

Fig. 2). This works because the η-reachability con-

dition ensures insensitiveness to exogenous perturba-

tions. Here, sliding motion just occurs a certain time.

So, the price is that sliding motion is not preserved

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

276

all the time; i.e., the reduced order dynamic motion

is not sustained all the time. But, it is not so impor-

tant from the robust control of view (mitigation of the

external perturbation). Moreover, we can commutate

between these sliding surfaces avoiding sliding mo-

tion; i.e., when the trajectory hits a sliding surface

(warranted by the η-reachability condition), commu-

tate to the other one (see Fig. 3). In Fig. 3, chatter-

ing occurs as a Zeno behavior, that is, the number of

switching in the control law tends to inﬁnite in ﬁnite

time.

0 2 4 6

−1

−0.5

0.5

Time(sec.)

0 0.2 0.4 0.6 0.8 1

−1

−0.8

−0.6

−0.4

−0.2

0 2 4 6

−3

−2

−1

Time(sec.)

Control law

Sliding

surfaces

Figure 3: Simulations results of the perturbed system with

(0) = 1 and x

(0) = 0 utilizing a second modiﬁed sliding

mode control.

4 CONCLUSIONS

Employing second-order dynamic systems, we evi-

denced that sliding motion is not required to keeping

insensitive property of sliding mode control. Also,

with the examples shown here, chattering is not per-

sistently exhibited. So, we have presented an impor-

tant observation about this topic, that we think it will

open further comments on it.

REFERENCES

Edwards, C. and Spurgeon, S. K. (1998). Sliding Mode

Control: Theory and Applications. Taylor and Fran-

cis, Ltd., UK, 1nd edition.

J. Y. Hung, W. G. and HUng, J. C. (1993). Variable struc-

ture control: A survey. In IEEE Trans. on Industrial

Electroncis. Vol. 40, No.1, 2–2.

Perruqueti, W. and Barbot, J. P. (2002). Sliding Mode Con-

trol in Engineering. Marcel Dekker, Inc., New York,

1nd edition.

SLIDING MODE CONTROL - Is it Necessary Sliding Motion?

277