ANALYSIS OF REMS GTS ERRORS DUE TO MSL ROVER AND

MARTIAN ENVIRONMENT

Eduardo Sebastián, Carlos Armiens and Javier Gomez-Elvira

Lab. de Robótica y Exploración Planetaria, Centro de Astrobiología, Ctra. Ajalvir Km.4, Torrejón de Ardoz, Spain

Keywords: Environmental monitoring, infrared temperature detection and sensor error sources.

Abstract: This paper analyses the external sources of error of the REMS GTS, a contactless instrument to measure

ground temperature that is part of the payload of the NASA MSL mission to Mars. Some environment

properties such us atmosphere opacity, solar radiance, ground emissivity and rover IR emissions are studied,

determining GTS characteristics. The article also proposes a simplified geometrical and thermal model of

the rover and environment in order to evaluate and quantify their influence in ground temperature

measurements. Finally, the article summarizes simulation results and provides solutions in order to improve

sensor accuracy.

1 INTRODUCTION

The GTS (Ground Temperature Sensor), one of the

REMS (Rover Environmental Monitoring Station)

instruments, is mainly dedicated to measure the

brightness temperature of Martian surface, using

three thermopiles detectors in three infrared IR

bands, and looking directly at the ground. The

selected channels are 8-14μm, 16-20μm and 14.5-

15.5μm.

In general it can be said that two error sources

are associated with contactless temperature

measurements. On the one hand internal sources, all

those related with the sensor, the amplifying

electronics, and also errors associated with

calibration and sensor degradation. On the other

hand we have the errors due to the environment. In

the case of the REMS GTS the environment shows

difficulties because of the uncertainty in Martian

surface emissivity, reflections from the rover and the

Sun, and atmosphere absorbance.

The main objective of this paper is to justify the

GTS design based on environment restrictions, as

well as to obtain a thermal model of the rover and

the environment in order to analyse and correct the

errors in ground temperature determination.

The paper is organized as follows; section 2

introduces briefly the REMS GTS; section 3

describes the environmental sources of error,

including a simplified radiation model of MSL

rover. Section 4 shows simulations to evaluate

environment influence, using the proposed model.

Finally, section 5 summarizes the results.

2 REMS GTS DESCRIPTION

REMS is an environmental station designed by the

Centro de Astrobiología with the collaboration of

national and international partners (CRISA/EADS,

Universidad Politécnica de Cataluña (UPC) and

Finish Meteorological Institute (FMI)), which is part

of the payload of the MSL (Mars Science

Laboratory) NASA mission to Mars, figure 1. This

mission is expected to launch in the final months of

2009, and mainly consists of a rover with a complete

set of scientific instruments.

Figure 1: NASA MSL rover.

205

Sebastián E., Armiens C. and Gomez-Elvira J. (2008).

ANALYSIS OF REMS GTS ERRORS DUE TO MSL ROVER AND MARTIAN ENVIRONMENT.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 205-210

DOI: 10.5220/0001505702050210

 SciTePress

The rover main body hosts the electronics

associated with the whole set of instruments, rover

communications and control systems. Additionally,

it includes the RTG (Radioactive Temperature

Generator) which is the rover energy source. The

RTG extra heat is used by rover thermal designers to

warm the rover body in order to keep alive the

electronics inside.

The GTS shall be mounted in one of the REMS

booms, which is placed in the rover mast at 1.6m

height and hosts the electronics dedicated to amplify

the thermopiles signals. The GTS includes an in-

flight calibration system without moving parts,

whose main goal is to compensate the sensor

degradation due to the deposition of dust over its

window (Sebastián and Gomez-Elvira, 2007). To

avoid local effects, the GTS focuses a large surface

area of around 100

m, shown in figure 2, measuring

the average temperature. This are is far enough from

the rover as to minimize its influence.

Figure 2: REMS GTS FOV and MSL rover simplified

draft.

3 GTS ERRORS DUE TO

MARTIAN ENVIRONMENT

Contactless temperature measurements are based on

the integration of the IR radiation coming from a

body. This radiation depends mainly on three

factors: The temperature of the focused area, the

emissivity

of its surface, or what is the same the

capacity of the body to emit IR energy, and finally

the reflectivity r of its surface, that shows how the

body reflects energy coming from the environment.

For the characteristic temperatures of Mars the

emitted radiation falls mostly in the IR range.

Following Wien's law, the maximum of the

blackbody spectral radiance for a given temperature

is given by

max

[μm]=2898/T[K]. If the maximal and

minimal Martian temperatures are T

max

=293K and

min

=150K then the sensor is designed to work

optimally in the range from 9.9μm to 19.3μm.

3.1 Atmosphere Transmission

Windows

The Martian atmosphere consists mostly of CO

which has a strongly absorbing band centred at

15μm. The CO

in the column of air within the cone

of view may also act as absorber and emitter (notice

that the air is generally at a very different

temperature from the ground) around the band.

Additionally, water molecules have a very strong

absorption at 1.45μm, and a weak absorption at

6.27μm (Martin, 1986).

3.2 Reflected Solar Radiance

Since the typical emissivities of Martian soils are

different from one, the IR Solar radiation shall be

added up to ground emissions (Lienhard and

Lienhard, 2006). Assuming that in the IR the Sun

radiance on the Martian surface is equal to the one

on top (inside atmosphere transmission windows),

and that the Martian ground IR reflectivity r=1-

with

the emissivity, is bounded to 0.1, one can

obtain the reflected flux as E

reflected

=r·E

sun

. The solar

flux on Mars surface is, F

sun

=E·(R

/D)

with

=6.96x10

m the Sun radius, D=1.52·1AU=

1.52·1.5x10

m the Sun to Mars distance, and where

E is the radiance of a blackbody emitting at a

temperature T=6000 K (Vázquez et al., 2005).

The measurements must be performed in a range

where the ratio of IR radiance emitted by the

Martian surface to the solar IR radiance reflected by

the Martian surface is significantly greater than one.

For instance, figure 3 shows that above 8μm the

solar reflected radiance is smaller than 0.5% for the

lower ground temperature, T

=150K.

Figure 3: Ratio ground signal/sun radiance vs. wavelength.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

206

Therefore, the GTS channels 8-14μm and 16-

20μm are selected taking into account the optimum

wavelength range from Wien’s law, but trying to

avoid the atmospheric absorption bands and the

wavelengths in which solar radiation cannot be

neglected. Each channel is specialised in the

measure of a temperature range where the higher

S/N ratio, based on the Planck’s law, is achieved

(Vázquez et al., 2005). The other GTS band 14.5-

15.5μm shall measure the temperature of Martian

atmosphere using for that the CO

emission band.

3.3 Reflected Rover Radiance

The MSL rover is a source of error for the GTS,

since some parts of it are subjected to temperatures

over the ground. These rover elements are mainly

the RTG and the rover body, which can reach

temperatures 200K and 50K over the atmosphere,

respectively. These elements are painted using high

emissivity paint, and their temperature shall be

recorded on line during Martian operation.

In order to evaluate rover influence as a source

of error in the determination of ground temperature

it is necessary a thermal conduction and radiation

model of Martian environment. In (Lee, 2006) the

heating process of ground surface by thermal

conduction due to the RTG is studied. The results

show a neglected influence in the area focused by

the GTS. On the other hand, figure 2 shows a

simplified geometrical representation of the

environment (GTS thermopiles, rover, atmosphere

and Martian surface), from which rover radiance

reflected on the ground can be estimated based on a

radiation diagram. The radiation model considers

that the IR energy reflected by the ground is

completely diffuse.

Eg·eg

Requç

Ea=0

Rg-a

Rg-s

Eg·eg

sgg

−

−1

1−

sgg

−

sgg

−

agg

−

Eg·eg

Requç

Ea=0

Rg-a

Rg-s

Eg·eg

sgg

−

−1

1−

sgg

−

sgg

−

agg

−

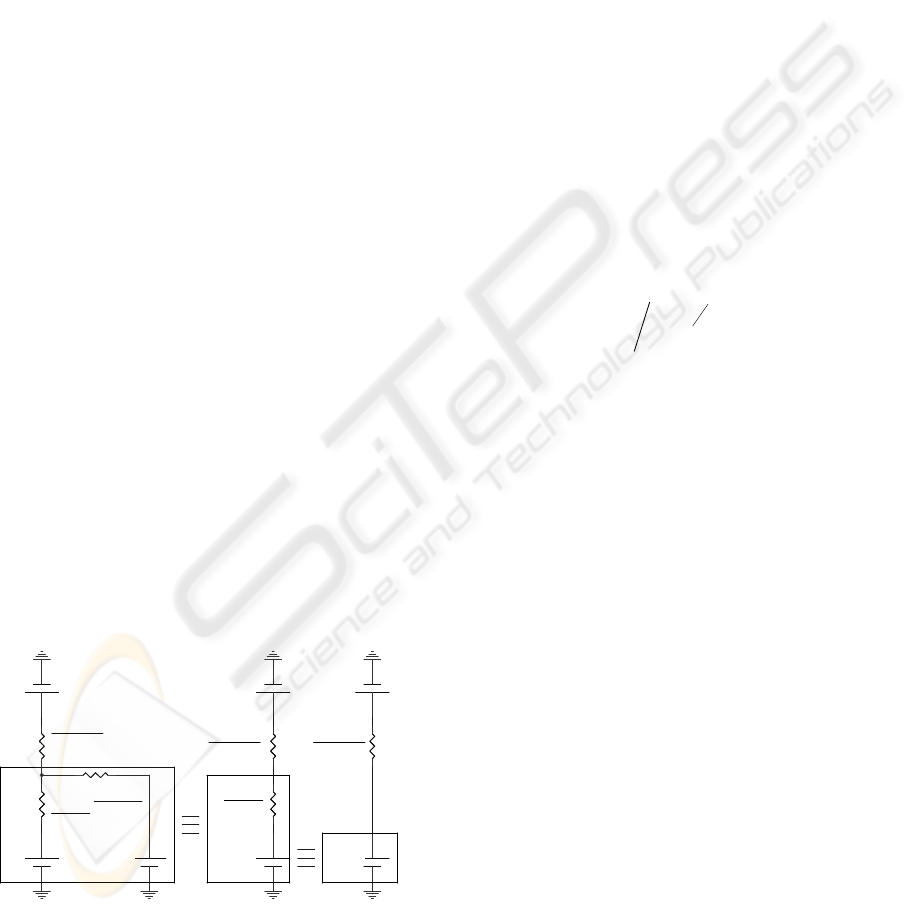
Figure 4: GTS and ground equivalent thermal circuit.

The first step in rover radiance influence analysis

considers an ideal situation in which the rover does

not exist. The circuit shown in figure 4 represents an

electrical analogy of the thermal model, in which

voltage generators and currents are equivalent to the

energy flux radiated by each body and the heat

exchange respectively and resistors represent surface

and geometry radiation resistances. The value of the

resistors depends on parameters such us the areas

and emissivities of the bodies, and the view factor

between them (Lienhard and Lienhard, 2006). The

atmosphere, as it was said before, is modelled as a

transparent body that does not emit energy inside the

measurement wavelengths, E

=0. In this way, A

represents the area of the ground seen by the GTS,

the emissivity of the ground, F

x-y

the view factor

between the bodies determined by the subscripts,

and finally E

represents the energy radiated by a

blackbody at the temperature of the body determined

by the subscript and inside the measurement band of

the thermopile. The subscript g is for ground, a is for

atmosphere and s is for the thermopiles. The

expression of E

follows Planck’s law and takes the

form,

[]

252

/1·2)·( mWdehcTE

∫

⎟

⎠

⎞

⎜

⎝

⎛

−=

λλλ

(1)

where T(

) is the thermopiles filter transmittance.

Figure 4 shows two successive simplifications of

the electrical circuit. The first one obtains an

equivalent circuit, assuming that the view factor F

g-a

is very close to the unit. This is reasonable because of

the small size of the thermopile and environment

geometry. The second simplification assumes two

things: first the view factor F

g-s

is very small and close

to zero, since the area of the thermopile compared with

the distance between the thermopile and the ground is

very small. Second,

takes real values that go from

0.9 to 1. Thus, the equivalent resistor is dominated by

the value of the geometry resistance.

This circuit gives us means for calculating the

heat exchange between the environment and the

sensor, whose temperature (T

) is known. From it,

and based on GTS thermopiles sensibility G

[V/W],

the output voltage of the thermopiles (2) can be

obtained. This voltage shall be considered as the

GTS ideal output, and shall be compared with the

real one, once the rover is included in the thermal

model. The result of this comparison shall be the

error introduced by rover heated bodies. In addition

to that, equation (2) depends on the value of ground

emissivity,

, which is an a priori unknown

parameter that introduces also uncertainty in ground

temperature determination.

ANALYSIS OF REMS GTS ERRORS DUE TO MSL ROVER AND MARTIAN ENVIRONMENT

207

EGV

Sout

Δ= ·

(

)

SggSgg

EEFAE −∈=Δ

−

···

(2)

The next step in rover influence analysis includes

the rover geometrical and thermal model. Figure 5

stars from a previous simplification of rover body

and RTG equivalent circuits. This simplification,

whose objective is to obtain the equivalent circuit

for these bodies and the atmosphere, is similar to the

carried out in figure 4 for Martian ground.

Eeq

Requ

(1-eg)/Ag

Rrtg-g

Rg-s

Rdeck-g

Rg-s

Eg·eg

Eeq

Edeck

Ertg

Rg-s

bodybody

equ

sgg

−

−1

sgg

−

sgg

−

RTGgg

−

equ

RTGRTG

−1

bodygg

−

Eeq

Requ

(1-eg)/Ag

Rrtg-g

Rg-s

Rdeck-g

Rg-s

Eg·eg

Eeq

Edeck

Ertg

Rg-s

bodybody

equ

sgg

−

−1

sgg

−

sgg

−

RTGgg

−

equ

RTGRTG

−1

bodygg

−

Figure 5: GTS, rover body and ground equivalent thermal

circuit.

The equivalent resistance of the squared area of

figure 5 can be easily calculated, assuming that view

factors between ground and rover body (F

g-body

) and

ground and RTG (F

g-RTG

) take values close to zero.

Thus, the resistor inside the ground branch of the

circuit is much smaller than the others, and its value

dominates. Equally, the calculation of the equivalent

generator of the squared area E

equ

needs to solve the

equations system (3) for I

and substitute its value in

(4). And finally, the second simplification follows

the same reasoning of figure 4.

()

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

+∈−

⎥

⎦

⎤

⎢

⎣

⎡

∈−∈

−−

−

−−

−

···

1·1

··

FFA

FAFA

bodygRTGgg

bodygRTGg

RTGgg

RTGggRTGgg

RTGgg

bodybodyRTGRTG

RTGRTGgg

(3)

(

)

equ

IE ∈+

∈−

−= ·

(4)

Newly, equation (4) shows a dependency of

ground emissivity,

. In this case temperatures,

emissivities and view factors of rover body and RTG

appear additionally in the equation as a new source

of uncertainty.

4 SIMULATIONS ON ROVER

AND EMISSIVITY INFLUENCE

The development of practical test with a real or

scaled model of the MSL rover is extremely costly,

since Martian temperature ranges requires the usage

of complicate climatic chambers. From this point of

view, this chapter is dedicated to develop

preliminary simulations to evaluate or obtain a upper

bound of rover and ground emissivity influence in

the determination of Martian surface temperature.

The simulations are based on the GTS thermal

radiation model described in the previous section.

Then, to apply the model, the values of the view

factors and the ground area covered by the sensor

are required. In order to obtain practical data,

simulations using the software package Thermal

Desktop and a simplified geometrical model of the

problem similar to the shown in figure 2, have been

carried out. The model assumes that the rover and

the ground are in a horizontal plane. The results are

shown in table 1. Additionally, it must be pointed

out that the value of the energy terms, E

, are

obtained based on thermopiles practical data

(Sebastián and Gomez-Elvira, 2007).

Table 1: REMS GTS simulation data.

Body

T A F

g-x

GTS 1 T

+20K 1mm

1.99x10

-9

Ground 0.91-0.99 T

99.8m

Rover 0.8 T

+70K 0.0021

RTG 0.8 T

+220K 0.00101

Figure 6: Ground temperature determination error due to

ground emissivity uncertainty, supposing an emissivity

value of 0.95.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

208

The first simulation, figure 6, tries to analyse the

error associated to the determination of ground

temperature, generated by the uncertainty in ground

emissivity without taking into account rover effects.

Temperature error dada are provided for the

thermopiles 8-14μm and 16-20μm, considering an a

priory value for ground emissivity of 0.95. The

simulation is run for a possible range of Martian

ground temperatures, from 133K to 293K.

The second simulation, figure 7, analyses the

error introduced by rover body and the RTG. In this

case, ground emissivity is assumed to be known.

Figure 7: Ground temperature determination error due to

rover influence, supposing known values for ground

emissivities.

Finally, the last simulation, figure 8, includes the

errors associated to ground emissivity uncertainty

and rover body and RTG reflections, supposing a

value for the ground emissivity of 0.95.

Figure 8: Ground temperature determination error due to

rover influence and ground emissivity uncertainty,

supposing an emissivity value of 0.95.

5 CONCLUSIONS AND FUTURE

WORK

The selection of GTS measurement bands is

conditioned by Martian atmosphere optical

properties, ground temperatures as well as taking

into account solar reflected radiance, in order to

minimize or neglect the associated errors.

The REMS GTS location and orientation has

been selected in order to minimize rover influence,

due to the heating process of ground surface by

thermal conduction and rover indirect view

throughout ground reflected radiance. Additionally,

GTS field of view has been maximized in order to

increase signal to noise ratio, avoiding rover direct

vision.

Simulations on ground emissivity uncertainty

have shown an important error contribution in

ground temperature determination, reaching error

values of ±4K. This error is initially compliant with

GTS instrument required accuracy of ±5K,

nevertheless is so big that its contribution to the total

error budget must be reduced.

A possible solution to deal with this error resorts

to study the emissivity of similar soils to those found

on Mars. MSL mission includes a set of payload

instruments capable of providing detail information

about Martian soils composition. Thus, after

knowing the king of soil in which the rover is

operating, the studied emissivity value can be

applied.

Colour pyrometry techniques (Joners and

Gardner, 1980) are other possible solution, which

could be implemented in order to estimate ground

temperature and emissivity at the same time. A

possible algorithm consists of four equations (5)

with four unknown variables: the emissivities

8-14

and

16-20

, and ground temperatures T

and T

. The

first two equations are obtained from the equation

(2), particularized for the measurement bands (8-

14μm, 16-20μm). To complete the four equations a

new measurement for a different ground temperature

is required, while rover remains still in order to

assume constant the value of ground emissivity.

(

)

(

)

() ( )

2016

2,2016148

2,148

2016

1,2016148

1,148

−−−−

∈=∈=

equgg

equ

equgg

equ

TfETfE

(5)

The other source of error studied in this article,

rover over temperature effect, generates temperature

errors below ±0.4K, for the worst ground

temperature conditions. Initially, this error could be

neglected in comparison with others, and the

ANALYSIS OF REMS GTS ERRORS DUE TO MSL ROVER AND MARTIAN ENVIRONMENT

209

required GTS accuracy. However, this study

assumes some simplifications on environment

geometry and ground emissivity. For instance, frost

formation over the ground or different ground tilts

could modify rover reflectance, increasing error

contribution.

Therefore, an algorithm to compensate rover

influence could be required. The algorithm shall

necessarily be based on the model described in

section 3, subtracting in (4) the effect of the

undesired energy rover terms and solving for E

. In

order to do it, an estimation of

, A

, F

g-body

and F

RTG

, and the real temperatures of rover bodies are

required. The topography of the surface seen by the

sensor modifies the view factors between the

different environment objects. Thus, in order to

carry out this geometrical analysis it is necessary to

have a three-dimensional image of rover

environment, as well as rover position and

orientation. These data shall be provided by NASA.

Afterwards, they shall be used to obtain more

accurate view factors and areas, or just as a quality

control system to confirm the validity of the results.

For instance, CO

frost, shadows with different

ground temperature, or extreme ground tilts are

different circumstances to be detected.

A more rigorous analysis of rover influence and

a possible improvement in this algorithm must

include the sensibility of GTS versus the radiation

incident angle. Initially, the whole surface area seen

by the sensor is weighted equally, this is reasonable

for ground emitted radiation since the whole ground

is supposed to be at the same temperature.

Nevertheless, several small differentials of area, in

which the GTS sensibility is different, could be

considered instead of a unique ground area. So, IR

energy coming from the rover and reflected in these

differentials of area must be weighted considering

GTS sensibility. Equation 6 shows how the

geometrical resistor between ground and RTG

would be calculated,

∑

−RTGiggii

FAg ··

(6)

where A

is the differential of area i, F

g-RTGi

is the

view factor between the RTG and the differential of

area i, and g

is the weighting factor that considers

GTS sensibility. Sensibility depends on the incident

angle of the radiation and fulfils

∑

giig

AgA ·

Finally, the simplify model described in this

article must be confirmed using a specialized

software such us Thermal Desktop, evaluating the

global behaviour of the model and not only for

obtaining the value of the view factors.

ACKNOWLEDGEMENTS

The authors would like to express special thanks to

all members of the REMS project who are

collaborating in the development of the GTS.

REFERENCES

Joners T.P. Gardner J.L. 1980. Multi-wavelength radiation

pyrometry where reflectance is measured to estimate

emissivity. Phys. E: Sci. intrum., 1, 3006-319.

Lienhard IV J.H. and Lienhard V. J.H. 2006. A Heat

Transfer Textbook. web.mit.edu,3

edition.

Lee C. J. 2006. MSL study on RTG-to-Ground Interaction

Zone. Applied Sciences Laboratory, Inc. internal

report.

Martin T.Z. 1986. Thermal infrared Opacity Of The Mars

Atmosphere. Icarus, 66, 2-21.

Sebastián E. and Gomez-Elvira J. 2007. Preliminary tests

of the REMS GT-sensor, In ICINCO'07 International

Conference on Informatics in Control, Automation and

Robotics, Angers (France).

Vázquez L., Zorzano M.P., Fernández D., McEwan I.

2005. Considerations about the IR Ground

Temperature Sensor. CAB, REMS Technical Note.

Madrid.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

210