Transient IC Engine Monitoring Under Temperature

Changes Using an AANN

Xun Wang

, George W. Irwin

, Geoff McCullough

, Neil McCullough

and Uwe Kruger

Intelligent Systems and Control Research Group, Queen’s University Belfast BT9 5AH, U.K.

Internal Combustion Engines Research Group, Queen’s University Belfast BT9 5AH, U.K.

Department of Electrical Engineering

The Petroleum Institute, PO Box 2533, Abu Dhabi, U.A.E.

Abstract. This paper reports on non-linear principal component analysis for

fault detection on an internal combustion (IC) engine. An auto-associative

neural network (AANN) model is built from transient engine data collected

under varying atmospheric conditions. The experimental data used for

modelling was collected for two different drive cycles, the Identification Cycle

and the New European Drive Cycle. The key issue here is to decide which data

should be used for training the neural network to produce good fault detection

generalisation under different atmospheric conditions and with a different drive

cycle. This is achieved successfully, with the Q monitoring statistic indicating

an absence of unwanted false alarms under fault-free operation, along with

successful detection of air leaks of varying magnitude in the inlet manifold.

1 Introduction

The specific provisions of more general emissions legislation relating to the detection

of faults within an internal combustion engine is commonly known as On-Board

Diagnostics (OBD). This details both the component parts of the engine to be tested

and at what frequency. This monitoring entails the diagnosis of any fault, which could

cause the tailpipe emissions of carbon monoxide (CO), unburned hydrocarbons (HC)

and oxides of nitrogen (NO

) to rise above legislated values.

The automotive industry currently employs a combination of signal and model-

based diagnostic techniques for OBD, the latter being based mainly on physical

models of the system. However, as the emissions thresholds have reduced in response

to increasingly stringent regulation demands, the OBD fault detection thresholds have

tightened accordingly, thereby increasing the challenge in engine modelling and

monitoring (Stobart, 2003) with over 50% of engine control unit software being

currently devoted to OBD. The complexity of physical models will have to increase

dramatically if the smaller variations in emissions, constituting a fault under future

OBD regulations are to be successfully detected. Further, such models will require

extensive on-line validation for each engine and vehicle derivative. Consequently, the

cost of developing and validating physical models will increase exponentially. Over

Wang X., W. Irwin G., McCullough G., McCullough N. and Kruger U. (2008).

Transient IC Engine Monitoring Under Temperature Changes Using an AANN.

In Proceedings of the 4th International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 28-40

DOI: 10.5220/0001507900280040

 SciTePress

the last decade the mathematical complexity and computational intensity of physical

model-based OBD has stimulated research on alternative fault detection and diagnosis

approaches suitable for automotive engines (Nyberg, 1999; Grimaldi et al., 2001;

Crossman et al., 2003; Kimmich et al., 2005.)

Some work has also been done on statistical methods, including principal

component analysis (PCA) where a reduced set of statistically independent score

variables are generated for process monitoring. Unfortunately, while PCA in its

original form is only applicable to linear data, a nonlinear extension in the form of an

auto-associative neural network (AANN) (Kramer, 1992) is now available, where the

scores are produced in the network bottleneck layer. Because of its conceptual

simplicity and close relation to linear PCA, our previous work on diesel engines used

an AANN for monitoring during steady-state operation (Antory et al., 2005),

including increased sensitivity in detecting minor faults (Wang et al., 2008a) by

incorporating additional analysis in the form of the statistical Local Approach.

Nonlinear PCA (NLPCA) has also proved to be effective when applied to

experimental data recorded from the air intake system of a gasoline engine during

transient operation (Wang et al., 2008b). Here the AANN was trained on a modified

identification (MI) cycle, specially designed to ensure that the engine speed and

throttle position covered the complete operating map at rates similar to those

experienced during normal operation. Importantly, the resulting model proved

suitable for more general use with the New European Drive Cycle (NEDC), a

standardised test for all new model types representing a mixture of urban and

motorway driving. In this work also, rather than using the same operational cycle for

AANN training and testing, two completely different engine drive cycles will be

employed, as detailed later.

The major limitation in all the previous work is the absence of any consideration of

the effects of atmospheric changes on the ability of the model-based fault detection to

generalise in terms of avoiding false alarms while correctly identifying fault

conditions. Thus, the experimental data used for validating the AANN model and the

faulty data sets were all recorded under similar atmospheric temperature and pressure

conditions to those for the training data. Moreover, none of the measured engine

variables previously included in the monitoring model was in fact significantly

affected by such atmospheric changes. Any AANN model derived for IC engine

monitoring under laboratory conditions, should also be capable of being generalised

to a wider range of driving conditions. The aim of the present paper is to address this

important deficiency. The practical significance of the results reported later is that the

experimental data sets available for neural modelling not only covered two different

operational cycles, as required for dynamic monitoring, but were also recorded under

different temperature conditions.

Some work on the effect of changes in atmospheric pressure and temperature on

the performance of an engine has been reported in the literature, but from the

perspective of engine design (Sher, 1984). Here computer code was developed to

simulate the engine cycle for the purpose of evaluating an optimal engine design

giving the best performance at high altitude conditions. The focus of this paper is data

modelling of a modern automotive petrol engine, based on which its fault monitoring

under different driving conditions can be achieved. This further significantly extends

the generalisation abilities of the AANN IC engine model described in our previous

work.

The paper is organised as follows. An introduction to the experimental petrol IC

engine facility, the engine drive cycles and the data collection regime is given next in

Section 2. Following a brief review of NLPCA, Section 3 then presents the

experimental condition monitoring results. The paper ends with a brief discussion,

some conclusions and suggestions for future research.

2 Automotive Engine Tests

This section briefly describes the experimental engine test-bed, followed by detailed

explanations of the data collection regime under both normal and faulty operating

conditions.

2.1 Engine Test Cell

The target application was a four-cylinder 1.8 litre spark ignition engine,

manufactured by Nissan. This engine represents current technology with devices such

as variable valve timing, inlet swirl plates, exhaust gas recirculation and a close-

coupled catalyst. The engine installation can be seen in .

The engine was installed in a state-of-the-art test facility at Queen's University

Belfast. An AC dynamometer with a Ricardo S3000 controller was used to control the

engine throughout the simulated transient drive cycles. Sensor signals were recorded

using the testcell data acquisition hardware – a Ricardo TaskMaster 500/2000 system,

capable of recording up to 32 analogue input channels simultaneously.

Fig. 1. View of engine test-bed and dynamometer.

The intake subsystem of this engine was investigated. In order to simplify the air

intake modelling, the exhaust gas recirculation (EGR) function was disabled. The

following five variables were used to analyse this subsystem: crankshaft rotational

speed (rev/min), pedal position (%), mass air flow (kg/h), inlet manifold pressure

(bar) and inlet manifold temperature (ºC). Rotational speed and pedal position formed

the engine inputs, while the other variables represented the dynamic behaviour of the

intake system. Importantly, these variables are all available from current sensors fitted

to the standard vehicle and so the modelling and fault detection system for OBD

outlined in this paper requires no additional hardware.

In contrast to our previous work on this IC engine where atmospheric conditions

were not considered, it will be seen that including the inlet manifold temperature in

the data modelling allows atmospheric temperature changes to be incorporated, as

shown later in subsection 2.3.

2.2 Atmospheric Changes

The atmospheric temperature and pressure both affect the dynamic performance of an

IC engine and so must be accounted for in any model-based OBD scheme. This study

is confined to consideration of the variation in atmospheric temperature, since

atmospheric pressure control in the engine test cell was not available.

The experimental engine data sets were collected at two different temperature

conditions. Normal room temperature (RM) was around 20-25ºC and required no

manual intervention. The elevated temperature (ET) condition was controlled at 30-35

ºC by electrical heating of the combustion air. The engine’s performance under these

two temperature conditions is analysed below, after the two drive cycles have been

introduced.

2.3 Drive Cycles

The New European Drive Cycle (NEDC) is used for emissions certification of light

duty vehicles in Europe. It is composed of various sections which simulate both urban

and motorway driving conditions. The measurement of the resulting exhaust

emissions forms one component of the Type Approval test, which is compulsory for

any new vehicle model entering the European market. Alternative drive cycles

include the FTP 75 used in the USA and the 10-15 Mode Cycle adopted by Japan.

The variation in the engine speed and pedal position inputs produced by the NEDC

for a sampling rate of 10Hz are shown in the top two plots of Fig. 2. Note that Fig. 2

shows two experimental data sets, corresponding to the RM (black) and ET (red)

temperature conditions respectively. In addition to the five engine variables, the figure

also includes the atmospheric temperature. The reason for including the atmospheric

temperature is to help visualise the impact of its change on the engine performance.

This variable is not to be included in the subsequent engine modelling.

It is clear from Fig. 2 that the NEDC is a highly transient cycle which includes

periods of rapidly varying engine speed and pedal position inputs as gear changes are

simulated. During vehicle deceleration, when the pedal position is zero, the engine

speed is often higher than idle speed. Here the engine is motored through the

transmission which contributes to the vehicle’s braking requirement. These phases of

the NEDC were simulated during testing by supplying a torque input from the

motoring dynamometer to maintain the commanded engine speed.

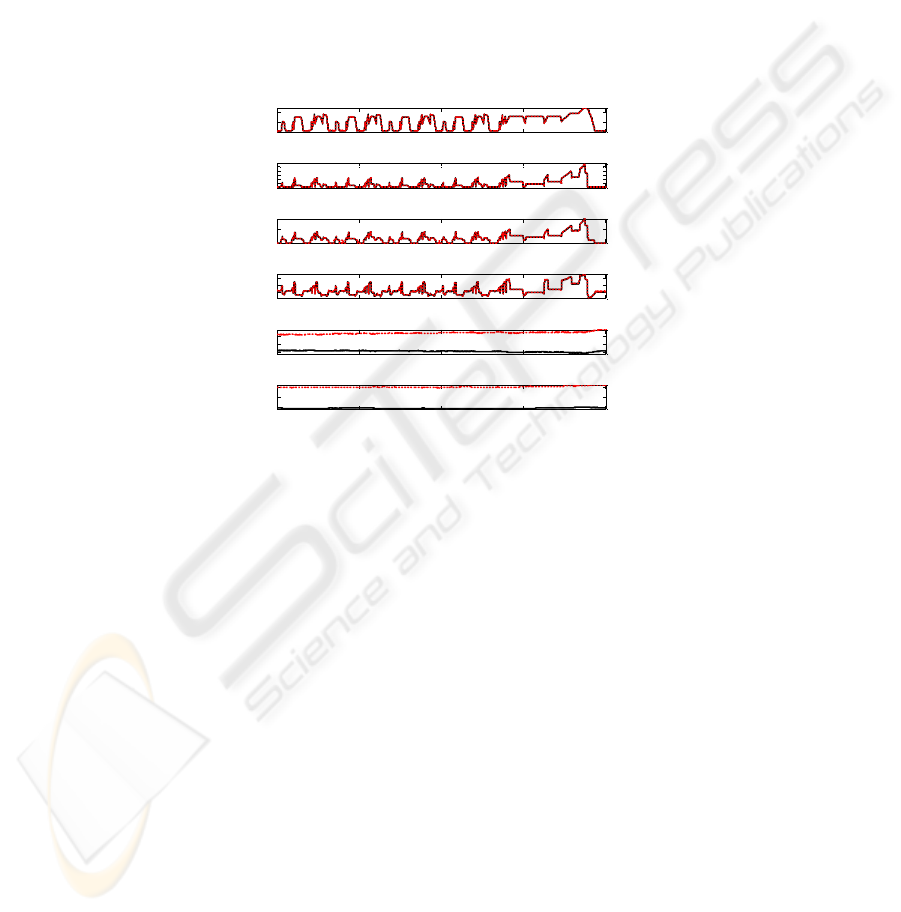
In the example shown in Figure 2, the temperature of the air drawn into the intake

manifold in the RM case is increased slightly above the atmospheric temperature due

to heat transfer from the warm engine. The average inlet manifold temperature is

therefore around 26

C. Conversely, in the ET case, the temperature of the air supplied

to the engine is higher than that of surrounding environment and so some heat is lost

by convection from the intake manifold, reducing its temperature to around 32

C on

average. Assuming the volumetric efficiency of the engine remains the same for a

given combination of inputs, the increase in temperature between the RM and ET

cases reduces the density of the air, and hence the mass air flow rate, entering the

engine by around 2%. The intake manifold pressure was unaffected by the change in

atmospheric temperature.

1000

3000

Engine Speed (rpm)

Pedal Position (%)

Mass Air Flow (g/sec)

0.4

0.8

Intake Manifold Pressure (bar)

Intake Manifold Temperature (ºC)

5 10 15 20

Atmospheric Temperature (ºC)

Time (min)

Fig. 2. Engine variables for the NEDC (10Hz sampling) with RM (black) and ET (red)

atmospheric temperatures.

While the NEDC is indeed a highly dynamic cycle, and is purported to be

representative of typical vehicle use,

Fig. 4 shows that the engine control inputs do not

cover the whole operational map. For example, engine speed does not exceed

3500rpm while the throttle pedal position is less than 15% for most of the cycle,

briefly reaching a maximum of around 28% at 3500rpm during the motorway driving

phase. This represents only 55% of the peak torque available at that engine speed.

This analysis implies that data from the NEDC would be unsuitable for training an

AANN model. Inaccurate predictions would be produced and false alarms generated,

when the IC engine is operated outside the regions of the map accessed during

training.

An alternative drive cycle, the Kimmich identification cycle (KI cycle), was also

considered to provide better coverage of the operating region (Kimmich et al., 2005).

However, although this cycle indeed produces a broader range of engine speeds and

throttle positions, the rate at which these variables change is very significantly lower

than that experienced in real driving. The NEDC by contrast is more dynamic in

nature and does produce more realistic transients. A modified identification (MI)

cycle was therefore designed to generate suitable data for transient modelling. This

was developed by examining the sections of the NEDC where the engine speed was

undergoing the greatest transients, which occurs during accelerations in 1st gear. The

timescale of the KI cycle was then reduced by a factor of 5.7 such that the rate of

change of engine speed matched that of the most transient section of the NEDC. The

resulting MI drive cycle therefore combines the benefits of both the KI one and the

NEDC as it produces good coverage of the engine operating map, while also

simulating realistic dynamics. The engine inputs for the MI cycle and corresponding

outputs for the same two cell temperature conditions as before are shown in Figure 3.

The same observation can be made as for the NEDC responses in Fig. 2 viz. that only

the inlet manifold temperature has been affected by the atmospheric temperature

change.

Comparing the operating maps of the MI and NEDC cycles in

Fig. 4, it is clear that

any model built on engine data from the former cycle will better represent a much

wider range of IC engine operation, as required.

2000

4000

Engine Speed (rpm)

Pedal Position (%)

Mass Air Flow (g/sec)

0.5

Intake Manifold Pressure (bar)

Intake Manifold Temperature (ºC)

1 2 3 4 5 6 7

Atmospheric Temperature (ºC)

Time (min)

Fig. 3. Engine variables for the modified identification (MI) cycle with RM (black) and ET

(red) atmospheric temperatures.

500 1000 1500 2000 2500 3000 3500 4000 4500

Engine Speed (rpm)

Throttle Position (%)

Fig. 4. Comparison of engine operating maps for the NEDC (circles) and MI (crosses) drive

cycles.

2.4 Data Collection

The MI cycle last about 8 minutes, providing 4785 data points. This cycle was

repeated three times for both RM and ET conditions without introducing any engine

fault. This generates two sets of engine data for model building, the third being

reserved to validate the model. A further single set of NEDC data was recorded

during normal ‘fault-free’ operation under both RM and ET conditions, in order to

assess the generalisation capability of the trained AANN model on unseen data.

2.5 Air Leak Fault

In this investigation, the faulty conditions took the form of air leaks of varying sizes

in the intake manifold. This is indicative of a process, rather than sensor fault, and is

representative of a leakage past a gasket or fitting between the throttle plate and the

intake valve. A minor air leak potentially may not be noticeable to the driver.

Nevertheless, when a fault of this type occurs, the driver would adjust the throttle

pedal until the desired torque is achieved. Thus, in this fault scenario it is imperative

to preserve the values of the engine speed and pedal position between the fault-free

and faulty conditions. The fault was introduced by drilling a hole into a bolt which

was then screwed into the inlet manifold of the engine downstream of the throttle

plate. A total of four such bolts were used: a solid one to produce the fault-free

condition, and three others with 2mm, 4mm, and 6mm diameter holes to introduce

faults of differing magnitude. Data representing all three faulty conditions were

collected for both the MI cycle and the NEDC.

3 Nonlinear PCA

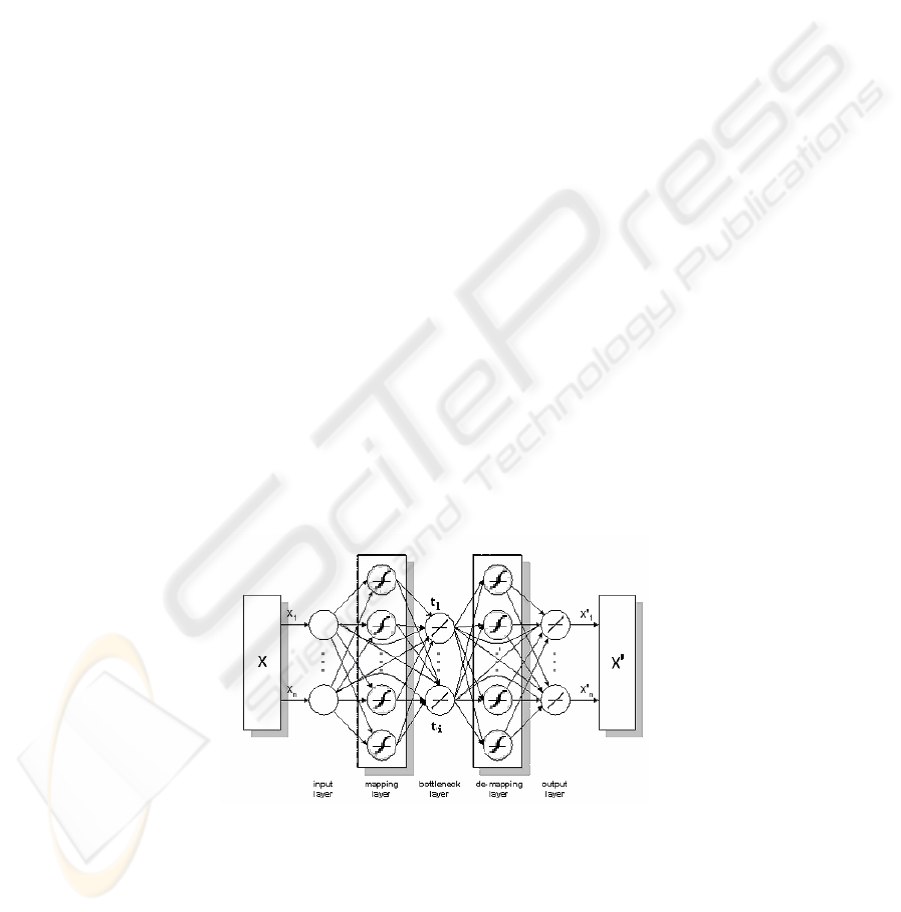
The AANN shown in Fig. 5 is a special neural network architecture with 3 hidden

layers, referred to as the mapping, bottle-neck, and demapping layers respectively.

Fig. 5. Auto associative neural network architecture for nonlinear PCA.

The AANN represents an identity mapping for a given set of n variables, such that

the network inputs and outputs are identical. A hyperbolic tangent function was used

as the activation function in the mapping and de-mapping layers, while the other two

layers contained linear activation functions. Note also the presence of direct links

from the inputs to the bottleneck layer and from the bottleneck layer to the outputs.

This network is regarded as a nonlinear version of PCA because of its similarity in

producing ‘scores’, normally fewer in number than the original variables from a given

process. The scores generated by linear PCA are based on the linear relationships

among the physical variables, and can effectively represent the variance in these

variables. The scores can then be used for reconstructing the original variables or for

monitoring any unknown data from the same process. In the case of NLPCA, the

ni < nodes in the bottleneck layer represent the nonlinear scores,

tt ,,

. They

are obtained by capturing the nonlinear relationship between the engine variables in

the input layer. The scores are then able to reconstruct the original variables by

passing them through the de-mapping layer to the output layer. If only linear

relationships exist between the engine variables, the scores from such a NLPCA

model should in theory be the same as those from a PCA one.

The mathematical description of the identity mapping can be described in two

parts. The scores are produced in Figure 5 by the mapping layer that constitutes a

nonlinear transformation on the inputs. Thus, for the k

score:

)(xt

(1)

The variables at the output layer

′

can then be obtained using:

(

)

ijj

tttHx "

′

(2)

The AANN network parameters are trained by minimising the cost function:

∑

′

−=

xxJ

)(

(3)

When the NLPCA has been trained from fault-free data, a Q statistic can be

calculated based on the model prediction error as

Q =

(4)

Here

refers to the difference between the model prediction vector and its

measured value for one sample. Q follows a central

distribution and appropriate

confidence limits can be estimated as discussed in Jackson, 1991. The values of the Q

statistic from the training data were used to calculate 95% and 99% confidence limits,

which are subsequently used as benchmarks for monitoring unknown data from the

engine.

4 Results

Choosing the best training set from the fault-free MI cycle data sets to use for AANN

training required careful consideration. Three data sets had been generated for each of

the two atmospheric temperature conditions. Moreover, the atmospheric temperature

varied by 2 or 3 degrees during the three repetitions of the MI drive cycle. Although

minor, this variation will have an impact on the generalisation of any engine model.

The principle used in selecting training data here was to choose the fault-free data

with the widest possible range of temperature conditions, while leaving adequate

fault-free data for validation. Closer inspection showed that data sets one and three,

under either RM or ET temperature conditions, provided a much wider range of

temperature coverage than any alternative pairing. The training data used in this work

therefore consisted of four MI cycles corresponding to data sets one and three under

each of RM and ET temperature conditions. The second data sets, collected under

both RM and ET temperature conditions were then employed for validation purposes.

Subsection 4.1 provides details of how the model was trained, along with its

validation on the MI cycle. The generalisation capability of the resulting engine

model is assessed in section 4.2, while its ability to detect air leak faults with the

engine operating under both the MI and NEDC cycles is presented in subsections 4.3

and 4.4 respectively.

4.1 Training and Validation

The NLPCA built on the training data had a 5-10-4-10-5 structure, with 10 nodes in

the mapping and de-mapping layers and 4 in the bottle-neck layer. Having trained the

model it was subsequently validated using a new set of data recorded during a fault-

free MI cycle. The performance of the model during this training and validation

process is illustrated by the variation in the Q statistic shown in Figure 6.

1000 2000 3000 4000 5000 6000 7000 8000 9000

-5

-4

-3

-2

data points

Q (log)

Fig. 6. Q statistic variation on fault-free MI cycle data collected under two atmospheric

temperature conditions for model validation.

Here the upper limit represents the 99% confidence level, whereas the lower one is

for a 95% threshold, both of which were derived from the Q statistic of the AANN

training data. The resulting numbers of violations shown for data recorded under both

the RM and ET conditions are statistically acceptable, confirming the modelling

validity of the trained AANN.

4.2 Generalisation

When a model is used in practice, the new operational inputs often take a form

previously unseen by the model during its training. This is particularly the case with

automotive IC engines, which impose a stringent requirement for generalisation if the

results are to be of practical significance. This aspect of the NLPCA model was

therefore challenged by comparing the measured and predicted values of both mass

air flow and manifold air pressure produced by the NEDC with the engine operating

under fault-free conditions. The excellent generalisation capability of the trained

AANN is supported by

Fig. 7, which shows the low numbers of violations of the

confidence limits by the Q statistic under both temperature conditions. This reveals

that there is little difference between the measured engine data and the corresponding

predictions. This is an important finding as the NEDC engine inputs of speed and

pedal position vary at rates ranging from steady-state up to the highly transient

conditions found during 1st gear accelerations and motored deceleration phases.

Moreover, the atmospheric conditions when these data sets were collected also

differed from those of the training data.

0.5 1 1.5 2

x 10

-5

-4

-3

-2

data points

Q (log)

Fig. 7. Q statistic variation on fault-free NEDC and two temperature conditions for model

generalisation.

4.3 Fault Detection on MI Data

This section assesses the AANN model’s ability to detect a fault produced by running

the MI cycle in the presence of a 2mm, 4mm, and 6mm air leak on the inlet manifold.

Fig. 8 and Fig. 9 show the variation in the corresponding Q statistics for data recorded

under RM and ET conditions respectively. It can be seen that in either case the

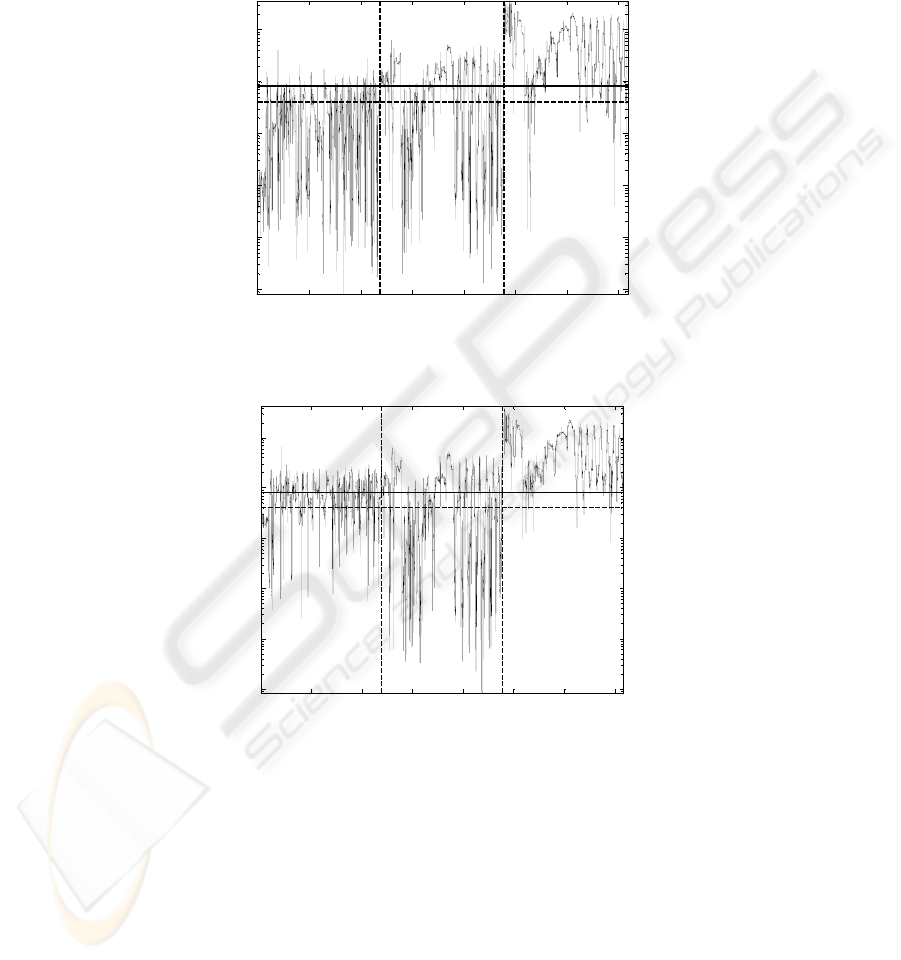
number of violations of the confidence limits naturally grows as the magnitude of the

fault increases. Since the 2mm air leak does not have a significant impact on the

engine performance, its Q statistic does not produce as many obvious violations to the

99% confidence limits as for the larger two air leaks. Even so, this minor fault can

still be detected by referencing to the 95% confidence limit.

2000 4000 6000 8000 10000 12000 14000

-6

-5

-4

-3

-2

-1

data points

Q (log)

2mm 4mm 6mm

Fig. 8. Monitoring 2mm/4mm/6mm air leak faults for the MI cycle at the RM temperature

condition.

2000 4000 6000 8000 10000 12000 14000

-6

-5

-4

-3

-2

-1

data points

Q (log)

2mm

4mm

6mm

Fig. 9. Monitoring 2mm/4mm/6mm air leak faults for the MI cycle at the ET temperature

condition.

It should be noted that there are certain regions in the faulty data set where the

impact of the air leak fault may not be apparent in the monitoring statistic. This is

expected, as this fault would not affect the engine when it is operating at high throttle

openings. Under such circumstances, the manifold pressure is close to, or equal to, the

atmospheric pressure. Consequently, the pressure difference across the leakage orifice

is small and the flow rate of air through it is therefore negligible.

4.4 Fault Detection on NEDC

The variations in Q statistic for the AANN model shown in

Fig. 10 and Fig. 11 cover

the three fault conditions for the NEDC under both RM and ET temperature

conditions respectively. Pleasingly, these results confirm successful detection of all

three air leak faults, despite the model having being trained using the substantially

different MI identification cycle.

0.5 1 1.5 2 2.5 3 3.5

x 10

-5

-4

-3

-2

-1

data points

Q (log)

2mm 4mm 6mm

Fig. 10. Monitoring 2mm/4mm/6mm air leak faults for the NEDC cycle at the RM temperature

condition.

0.5 1 1.5 2 2.5 3 3.5

x 10

-5

-4

-3

-2

-1

data points

Q (log)

2mm

4mm 6mm

Fig. 11. Monitoring 2mm/4mm/6mm air leak faults for the NEDC cycle at the ET temperature

condition.

5 Conclusions

This paper showed the capability of an AANN in both modelling and air-leak fault

detection for an automotive gasoline IC engine. The modelling data was derived for

two different transient drive cycles under different atmospheric temperature

conditions. The model trained using MI cycle data sets that were recorded under all

available atmospheric temperature conditions produced the best generalisation to

measurements from the unseen NEDC cycle. There was an absence of unwanted false

alarms under fault-free conditions, and successful detection of air leaks of varying

magnitude in the inlet manifold.

Acknowledgements

The authors are grateful to the U.K. Engineering and Physical Science Research

Council (Grant No. EP/C005457) for their financial support.

References

1. Antory, D., U. Kruger, G.W. Irwin and G. McCullough 2005. Fault diagnosis in internal

combustion engines using nonlinear multivariate statistics. Proc Institution of Mechanical

Engineers, Part I: Journal of Systems and Control Engineering, 219(4), 243-258.

2. Crossman, J.A., H. Guo, Y.K. Murphey and J. Cardillo 2003. Automotive signal fault

diagnostics – part I: signal fault analysis, signal segmentation, feature extraction and quasi-

optimal feature selection. IEEE Transactions on Vehicular Technology 52(4), 1063-1075.

3. Grimaldi, C.N. and F. Mariani 2001. OBD Engine Fault Detection Using a Neural

Approach. SAE Paper No. 2001-01-0559.

4. Jackson, J.E. 1991. A Users Guide to Principal Components. Wiley Series in Probability

and Mathematical Statistics. John Wiley, New York.

5. Kimmich, F., A. Schwarte and R. Isermann 2005. Fault detection for modern diesel engines

using signal- and process model-based methods. Control Engineering Practice 13, 189-203.

6. Kramer, M.A. 1992. Autoassociative neural networks. Computers and Chemical

Engineering 16(4), 313-328.

7. Nyberg, M. 1999. Model Based Diagnosis of Both Sensor Faults and Leakage in the Air-

Intake System of an SI Engine. SAE Paper No. 1999-01-0860.

8. Sher, E. 1984. Effect of atmospheric conditions on the performance of an air-borne two-

stroke spark-ignition engine. Proc Institution of Mechanical Engineers, Part D: Transport

Engineering. 198(15), 239-251.

9. Stobart, R. 2003. Control oriented models for exhaust gas aftertreatment; A Review and

Prospects, SAE Paper No. 2003-01-1004.

10. Wang, X., U. Kruger, G.W. Irwin, G. McCullough and N. McDowell 2008a. Nonlinear

PCA with the local approach for diesel engine fault detection and diagnosis, IEEE Trans.

Control Systems Technology 16 (1), 122-129

11. Wang, X., G.W. Irwin, G. McCullough, N. McDowell and U. Kruger 2008b. Application of

nonlinear dynamic PCA to automotive engine modelling and fault monitoring, Control

Engineering