Forecasting Internet Trafﬁc by Neural Networks

Under Univariate and Multivariate Strategies

Paulo Cortez

, Miguel Rio

, Pedro Sousa

and Miguel Rocha

Department of Information Systems/R&D Algoritmi Centre

University of Minho, 4800-058 Guimar˜aes, Portugal

Department of Electronic and Electrical Engineering, University College London

Torrington Place, WC1E 7JE, London, U.K.

Department of Informatics, University of Minho, 4710-059 Braga, Portugal

Abstract. By improving Internet trafﬁc forecasting, more efﬁcient TCP/IP traf-

ﬁc control and anomaly detection tools can be developed, leading to economic

gains due to better resource management. In this paper, Neural Networks (NNs)

are used to predict TCP/IP trafﬁc for 39 links of the UK education and research

network, under univariate and multivariate strategies. The former uses only past

values of the forecasted link, while the latter also uses the trafﬁc from neigh-

bor links of the network topology. Several experiments were held by considering

hourly real-world data. The Holt-Winters method was also tested in the com-

parison. Overall, the univariate NN approach produces the best forecasts for the

backbone links, while a Dijkstra based NN multivariate strategy is the best option

for the core to subnetwork links.

1 Introduction

Internet trafﬁc prediction is a key issue for understanding communication networks and

optimizing resources (e.g. adaptive congestion control and proactive network manage-

ment), allowing a better quality of service [1–3]. Moreover, trafﬁc forecasting can help

to detect anomalies (e.g. security attacks, viruses or an irregular amount of SPAM) by

comparing the real trafﬁc with the forecasts [4,5].

TCP/IP trafﬁc prediction is often done intuitively by network administrators, with

the help of marketing information (e.g. future number of costumers) [1]. Yet, this may

not be suited for serious day-to-day network administration and the alternative is to

use Operational Research and Computer Science methods. In particular, the ﬁeld of

Time Series Forecasting (TSF), deals with the prediction of a chronologically ordered

variable, where the goal is to model a complex system as a black-box, predicting its

behavior based in historical data [6]. The TSF approaches can be divided into univariate

and multivariate, depending if one or more variables are used. Multivariate methods are

likely to produce better results, provided that the variables are correlated [7].

Cortez P., Rio M., Sousa P. and Rocha M. (2008).

Forecasting Internet Trafﬁc by Neural Networks Under Univariate and Multivariate Strategies.

In Proceedings of the 4th International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 61-70

DOI: 10.5220/0001508600610070

 SciTePress

Several TSF methods have been proposed, such as the Holt-Winters [6] and Neural

Networks (NN) [8,3]. Holt-Winters was developed for series with trended and seasonal

factors and more recently a double seasonal version has been proposed [9]. In contrast

with the conventional TSF methods (e.g. Holt-Winters), NNs can predict nonlinear se-

ries. In the past, several studies have proved the predictability of network trafﬁc by using

similar methods. For instance, the Holt-Winters was used in [4, 10] and NNs have also

been proposed [11,5, 3]. However, these studies only considered univariate (or single

link) data, thus not making use of the topology network. By using data from more than

one link, there is a potential for better predictions.

This study will use recent hourly data from the United Kingdom Education and

Research Network (UKERNA) network. The network includes a backbone made up of

8 core routers that transport data through 21 regional subnetworks. In this paper, we

will explore NNs and two multivariate approaches for data selection: using all direct

neighbor links and selecting the most probable neighbor that is expected to inﬂuence

the predicted link. The latter strategy is based in a novel heuristic that uses the Open

Shortest Path First (OSPF) [12] protocol and Dijkstra algorithm. These approaches will

be compared with the NN univariate case and also the classic Holt-Winters method.

Furthermore, we will predict all UKERNA core to core and core to subnetwork links,

in a total of 39 connections.

2 Internet Trafﬁc Data

This work will analyze trafﬁc data (in Mbit/s) from the UK academic network backbone

(UKERNA)

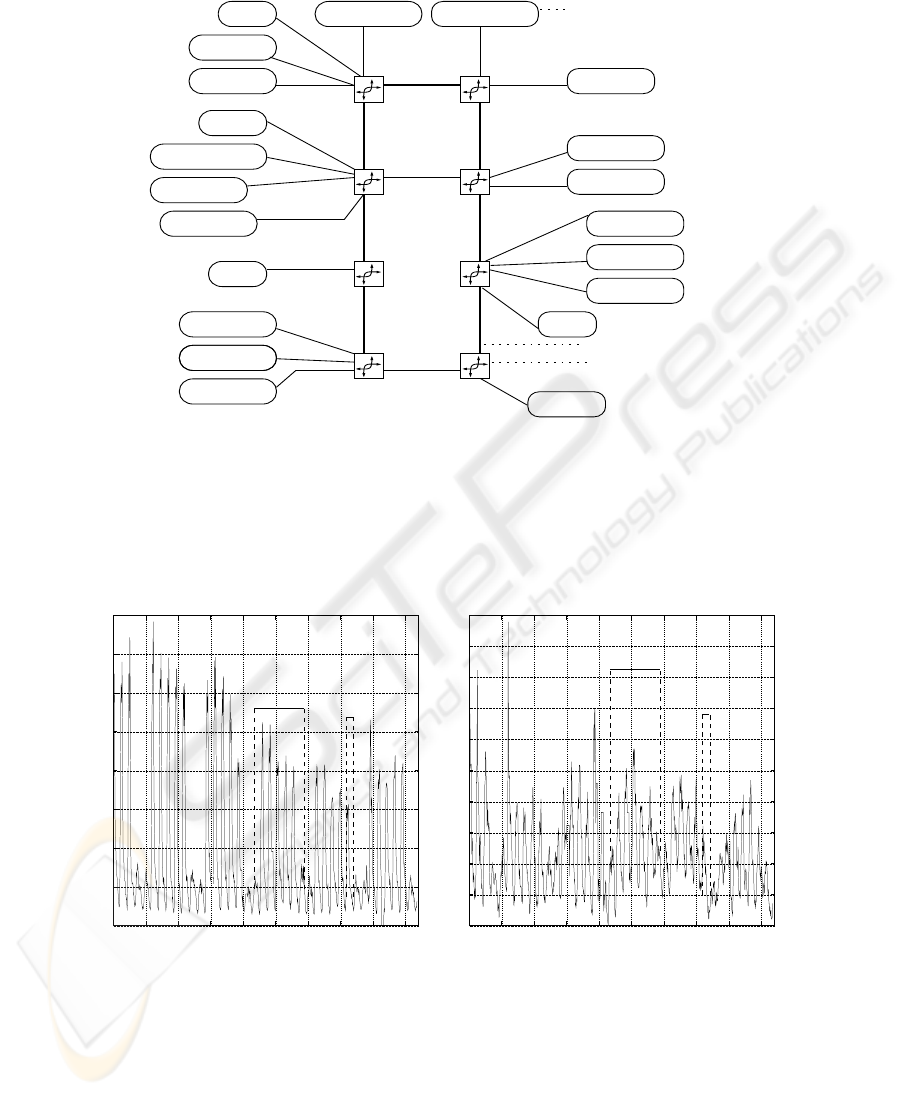
, which includes eight core routers and 21 subregional networks. Figure 1

plots the respective direct graph, where bdd, sdd and cdd denote the links within the

backbone core routers, core to subnetwork and subnetwork to core, respectively (d is

a digit number). The data collection was based in the Simple Network Management

Protocol (SNMP), which quantiﬁes the trafﬁc passing through every network interface

with reasonable accuracy [13]. SNMP is widely deployed by every Internet Service

Provider/network and the collection of this data does not induce any extra trafﬁc on the

network. In this work, we will adopt an hourly scale, denoting a short-term forecasting

that is often used to for optimal control or detection of abnormal situations [14]. The

data was recorded from 12 AM of 14th June 2006 to 12 AM of 23th July 2006. In total,

there are 936 hourly observations for each link.

The OSPF is the the most commonlyused intra-domainroutingprotocol[12]. Under

this protocol, every link contains a weight that is assigned by the network administrator.

The Dijkstra algorithm is used to ﬁnd the shortest paths between any two nodes of

the network and these paths are then used by the routers to direct trafﬁc. Most of the

UKERNA OSPF weights are set to 10 and the few exceptions are listed in Figure 1. For

instance, the OSPF weight between the core routers of Glasgow and Edinburgh is 100

(links b09 and b18); and the shortest path between Warrington and Edinburgh includes

the links b07 and b18.

http://www.ja.net

core router

CoshamBristol

Reading

Leeds

EdinburghGlasgow

Clydenet

NIRAN

FatMAN

Warrington

NWMAN

C&NLMAN

NNW

UHI

MidMAN

TVN

SWMAN

SWERN1

SWERN2

AbMAN

NorMAN

YMMAN

b18

b01

b02

b04

b05

100

100 111

100

112

100

b03

b06

b07

b08

b09

b10

b11

b12

b13

b14

b15

b16

b17

EastMAN

LeNSE

s17

s18

c18

s15

c17

c16

s16

c15

c10

s10

s11 c11

s20

c20

s13

s02

c02

c13

s19

s03

c03

150

c12

c19

c07

s12

s07

s04

subnetwork

c04

c01

s01

s14

c21

s21

c14

EMMAN

EastNET

KentMAN

s06

c06

s05

c05

c08

s08

London

LMN

c09

s09

100

backbone link

Fig.1. The schematic of the UK academic Internet network.

As an example, the trafﬁc of two neighbor links, Warrington-Glasgow (b07) and

Glasgow-Clydenet (s05), is plotted in Figure 2. In both graphs, there are inﬂuences of

two seasonal components due to the the intraday and intraweek cycles.

weekly cycle

daily cycle

100

200

300

400

500

600

700

800

0 100 200 300 400 500 600 700 800 900

Traffic (Mbits/s)

Time (hours)

daily cycle

weekly cycle

100

110

0 100 200 300 400 500 600 700 800 900

Traffic (Mbits/s)

Time (hours)

Fig.2. The IP trafﬁc for b07 (Warrington-Glasgow, left) and s03 (Glasgow-Clydenet, right) links.

3 Forecasting Methods

A Time Series Forecasting (TSF) model assumes that past patterns will occur in the

future. Let y

= (y

, . . . , y

) denote a multivariate series, where y

is the jth chrono-

logical observation on variable i and k is the number of distinct time variables (k = 1

when a univariate setting is used). Then [7]:

= F (y

1t−1

, . . . , y

1t−n

, . . . , y

kt−1

, . . . , y

kt−n

)

= y

− by

(1)

where by

denotes the estimated value for the pth variable and time t; F the underlying

function of the forecasting model; and e

is the error (or residual).

The overall performance of a model is evaluated by a global accuracy measure,

namely the Root Mean Squared Error (RMSE) and Relative RMSE (RRMSE), given in

the form [15]:

RM SE

P +N

i=P +1

RRM SE

= RMSE

/RM SE

× 100 (%)

(2)

where P is the presenttime; N is the number of forecasts; and RMSE

is the RMSE

given by the simple mean prediction. The last metric (RRMSE) will be adopted in this

work, since it has the advantage of being scale independent, where 100% denotes an

error similar to the mean predictor (y

Due to the temporal nature of this domain, a sequential holdout will be adopted for

the forecasting evaluation. Hence, the ﬁrst T R = 2/3 of the series will be used to ﬁt

(train) the forecasting models and the remaining last 1/3 to evaluate (test) the forecast-

ing accuracies. Also, an internal holdout procedure will be used for model selection,

where the training data will be further divided into training (2/3 of T R) and validation

sets (1/3 of T R). The former will be used to ﬁt the candidate models, while the latter

will be used to select the models with the lowest error (RMSE). After this selection

phase, the ﬁnal model is readjusted using all training data.

3.1 Neural Networks

Neural Networks (NNs) are innate candidates for forecasting due to their nonlinear and

noise tolerance capabilities. Indeed, the use of NNs for TSF began in the late eighties

with encouraging results and the ﬁeld has been growing since [8,14, 11,3].

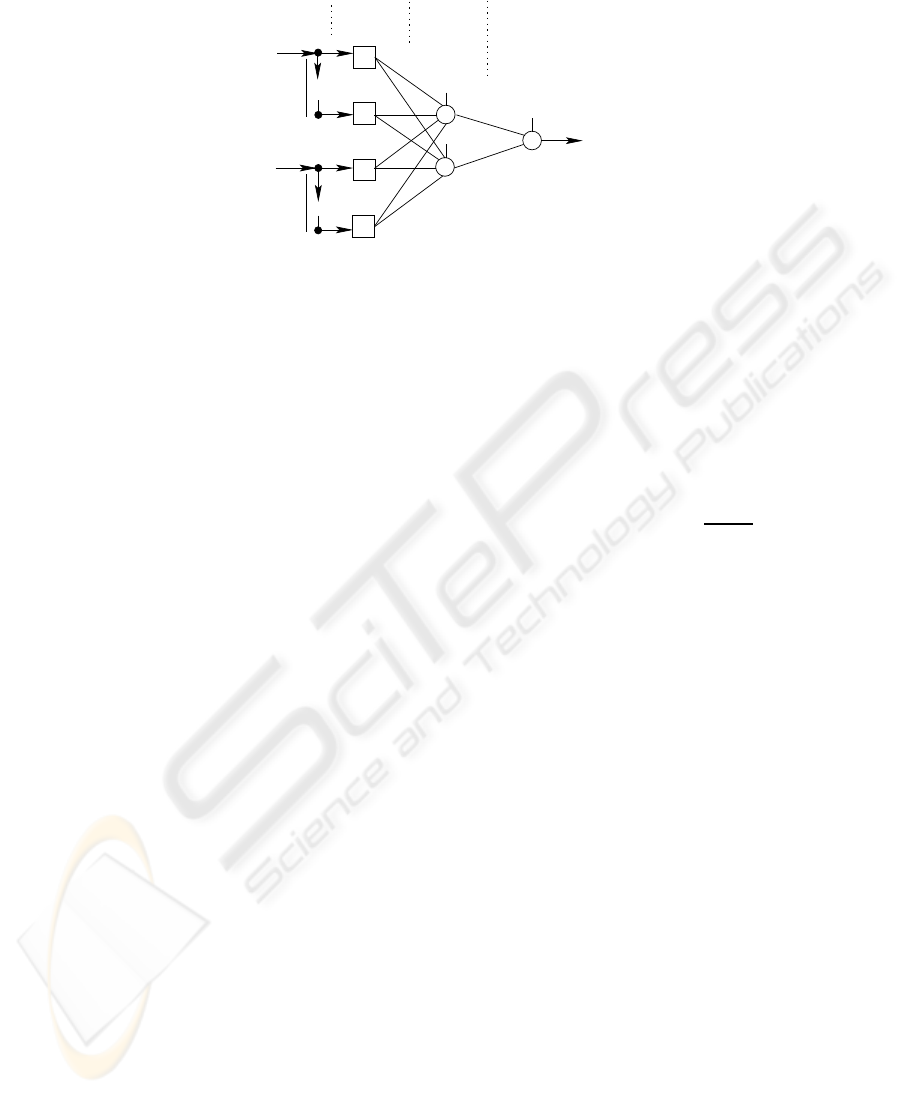
The multilayer perceptron is the most popular NN used within the forecasting do-

main [8, 11]. When adopting this architecture, TSF is achieved by using a sliding time

window

. A sliding window is deﬁned by the set of time lags used to build a forecast.

For instance, given the univariate time series 1,2,3,4,5,6 and sliding window {1, 2, 4},

the following training examples can be built: 1, 3, 4 → 5 and 2, 4, 5 → 6. In a multi-

variate setting, k sliding windows are used: {L

, . . . , L

}, . . . , {L

, . . . , L

where L

denotes a time lag for the ith variable.

In this work, a fully connected multilayer network with one hidden layer of H

hidden nodes and bias connections will be adopted (Figure 3). The logistic activation

This combination is also named Time Lagged Feedforward Network (TLFN) in the literature.

...

Output

...

1t−L

...

1t−L

kt−L

...

Series

Multivariate

Layer

Input

Layer

Hidden

...

i,j

window 1

window k

time

time k1

Fig.3. The multilayer perceptron architecture for multivariate time series forecasting.

function is applied on the hidden nodes and the output node uses a linear function [16].

In past work [3], this architecture outperformed conventional univariate methods such

as Holt-Winters and ARMA models. The overall model is given in the form:

= w

o,0

I+H

i=I+1

s=1

r=1

st−L

i,j

)

(3)

where w

d,s

is the weight from node s to d; (if d = 0 then it is a bias connection); j ∈

{1, . . . , I} is an input node; o is the output node; and f the logistic function (

1+e

−x

Before training, all variables are scaled with a zero mean and one standard devia-

tion. Then, the initial NN weights are randomly set within [−0.7, +0.7] [17]. Next, the

training algorithm is applied and stopped when the error slope approaches zero or after

a maximum of E epochs. Since the NN cost function is nonconvex(with multiple min-

ima), NR runs are applied to each neural setup, being selected the NN with the lowest

mean error [16]. After training, the NN outputs are rescaled to the original domain.

Under this setting, the NN performance will depend on the number of hidden nodes

(H), the selection of the k variables used in the multivariate model and the time window

used for each variable. All these parameters can have a crucial effect in the forecasting

performance. Feeding a NN with uncorrelated variables or time lags may affect the

learning process due to the increase of noise. A NN with 0 hidden neurons can only

learn linear relationships and it is equivalent to the classic Auto-Regressive(AR) model.

By increasing the number of hidden neurons, more complex nonlinear functions can be

learned but also it increases the probabilityof overﬁtting to the data and thus loosing the

generalization capability. Since the search space for these parameters is high, heuristic

procedures will be used during the model selection step.

Three strategies are proposed for the variable selection:

– Single-Link NN (SLNN), the simple univariate model where the predictions are

based on the past values of the current link (p);

– All Direct Neighbor Link NN (ADNN), based on p plus the previous trafﬁc ob-

served in all direct neighbor links that inﬂuence p; and

– Dijkstra-Assisted NN (DANN), based on p plus the neighbor that is expected to

inﬂuence more the predicted link under the OSPF protocol. First, the Dijkstra algo-

rithm is used to compute the shortest OSPF paths between all nodes of the network.

Then, the subset with all paths that include p as an internal or end link is selected.

Finally, the heuristic selects the most common

direct preceeding neighbor of p in

the subset.

Regarding the multivariate methods, DANN selects only k = 2 variables, while ADNN

uses a higher numberof links (from3 to 7). For instance, when forecasting the Reading-

TVN (p=s18) trafﬁc, the ADNN variable set is {s18,b05,b01}

(Figure 1). There are 16

OSPF paths ending at TVN that include b05 and only 11 paths that go through b01.

Hence, DANN will select the former (i.e. {s18, b05}).

Based on previous univariate IP trafﬁc forecasting work [3], a small range of hidden

nodes will be tested, with H ∈ {0, 2, 4, 6}. Also, three sliding windows, based on the

daily (K

= 24) and weekly (K

= 168) cycles, will be considered: w

= {1, 24, 25},

= {1, 168, 169} and w

= {1, 24, 25, 168, 169}. In [3], this sliding window setup

obtained high quality results. When a multivariate model is used, then the same window

is applied to all links.

3.2 Holt-Winters Methods

The Holt-Winters (HW) [6] is a popular univariate forecasting technique from the fam-

ily of Exponential Smoothing methods. The predictive model is based on some under-

lying patterns such as a trend or a seasonal cycle (K

), which are distinguished from

random noise by averaging the historical values. Its popularity is due to advantages

such as the simplicity of use, the reduced computational demand and the accuracy of

the forecasts, specially with seasonal series.

The general model is deﬁned by:

Level S

= α

t−K

+ (1 − α)(S

t−1

+ T

t−1

)

Trend T

= β(S

− S

t−1

) + (1 − β)T

t−1

Seasonality D

= γ

+ (1 − γ)D

t−K

= (S

t−1

+ T

t−1

) × D

t−K

(4)

where S

, T

and D

stand for the level, trend and seasonal estimates, K

for the sea-

sonal period, and α, β and γ for the model parameters. When there is no seasonal

component, the γ is discarded and the D

t−K

factor in the last equation is replaced

by the unity. More recently, this method has been extended to encompass two seasonal

cycles (K

and K

) [9]. In this work, four HW variants will be tested in the model

selection phase: n – non seasonal (K

= 1); d – daily seasonal (K

= 24); w – weekly

seasonal (K

= 168); and D – double seasonal (K

= 24 and K

= 168).

4 Experiments and Results

The experiments were conducted off-line (i.e. after the data was collected) using the

RMiner [18],an open source library for theR statistical environment[19]. Inparticular,

In case of a draw (which rarely occurs), the heuristic simply selects one of the contenders.

The link c18 is not considered, since its origin (TVN) matches the link destination.

the RMiner uses the nnet package [17] to implement the NNs. The NNs were trained

with E = 100 epochs of the BFGS algorithm [20], from the family of quasi-Newton

methods and the number of runs was set to NR = 10. The HW initial values (e.g. level

estimate) were set by averaging the early observations [9] and the internal parameters

(e.g. α) were optimized using a 0.05 grid search for the best training error (RM SE).

Since the intention is to compared univariate and multivariate approaches, only the

links with preceding neighbors will be predicted, i.e., all sdd and bdd, in a total of 39

connections. The selected forecasting models for each method are shown in Table 1.

For the HW, the weekly cycle is the most common model (w) and the double seasonal

variant is never used. The weekly effect (w

) is also the most common case for strategy

ADNN. In contrast, the majority of the SLNN and DANN methods use the double

seasonal model (w

). Regarding the NN architectures, in general only linear models

are selected. The 15 nonlinear exceptions (H > 0) are listed in the table. These results

conﬁrm the notion that short term IP trafﬁc can be modeled by small networks.

The forecasts with the selected models were performed on the test sets (with 312

elements) for all links shown in Table 1. Thirty runs were applied for the NNs and the

results are shown as the mean RRMSE with the respective 95% t-student conﬁdence

intervals. The range of the best RRMSE values is high, showing that some links are

much harder to predict than others (e.g. 14.1% for b10 versus 82.5% for s02). Overall,

the HW is the worst strategy, since it is the best method for only 2 links (b05 and b14).

Regarding the backbone links, the univariate approach (SLNN) is the best NN choice

in 10 cases, followed by the ADNN (best in 7 links), while the DANN outperforms the

other methods for only one link (b17). This scenario changes when considering the core

to subnetwork links (sdd), where the DANN is the best method (with 12 wins), while

both SLNN and ADNN achieve statistically signiﬁcant lowest errors in 4 cases.

For demonstrative purposes, the left of Figure 4 presents the average DANN trafﬁc

forecasts for the ﬁrst 60 hours ofthe s03 series. In this case, a high quality ﬁt is achieved,

since the two curves are close. The observed (x-axis) versus the predicted values for

a given run (y-axis) is also shown. In the ﬁgure, the forecasts (points) are near the

diagonal line, which denotes the perfect forecast. Another relevant issue is related with

the computational complexity. The proposed solution is very fast and can be used in

real-time. For the example, with a Pentium Dual Core 3GHz processor, the DANN

model selection phase took 12 seconds, while the 30 runs of the ﬁnal NN training and

testing required only 2.2 seconds.

5 Conclusions

This work analyses the efﬁciency of several Neural Network (NN) approaches when

applied to predict hourly TCP/IP trafﬁc, collected from the United Kingdom Education

and Research Network (UKERNA). In particular, three strategies were tested: SLNN –

univariate approach based on past patterns from the current link; ADNN – which also

includes the past values from all direct neighbors; and DANN – a novel approach that

includes only one link neighbor, whose selection is based on the Dijkstra algorithm and

OSPF protocol. Also, a comparison was made with the Holt-Winters (HW) method,

which is popular for seasonal series.

Table 1. The forecasting RRM SE errors and selected models (in brackets).

Link SLNN ADNN DANN HW

b01 24.8±0.0 (w

) 23.9±0.0 (w

) 25.0±0.0 (w

) 25.2 (w)

b02 63.2±0.0 (w

) 89.5±0.0 (w

) 63.4±0.0 (w

) 68.7 (n)

b03 22.1±0.0 (w

) 22.1±0.0 (w

) 22.2±0.0 (w

) 27.8 (d)

b04 21.3±0.0 (w

) 21.5±0.0 (w

) 22.2±0.0 (w

) 25.2 (w)

b05 34.1±0.0 (w

) 34.7±0.0 (w

) 35.7±0.0 (w

) 34.0 (w)

b06 86.6±2.7 (w

, H=4) 58.1± 0.0 (w

) 58.4±0.0 (w

) 69.0 (w)

b07 19.7±0.0 (w

) 30.6±0.0 (w

) 20.3±0.0 (w

) 25.1 (w)

b08 40.7±0.0 (w

) 40.7±0.0 (w

) 41.2±0.0 (w

) 44.3 (w)

b09 56.5±0.0 (w

) 57.2±0.0 (w

) 57.5±0.0 (w

) 67.5 (w)

b10 14.1±0.0 (w

) 17.7±0.0 (w

) 15.4±0.0 (w

) 15.0 (w)

b11 54.1±0.0 (w

) 57.3±0.9 (w

, H=2) 54.3±0.0 (w

) 58.0 (n)

b12 62.7±5.9 (w

, H=2) 36.1± 0.0 (w

) 74.6±0.0 (w

) 45.4 (w)

b13 30.5±0.0 (w

) 31.2±0.0 (w

) 30.6±0.0 (w

) 31.7 (w)

b14 19.5±0.0 (w

) 19.4±0.0 (w

) 19.5±0.0 (w

) 19.0 (w)

b15 79.9±0.0 (w

) 78.7±0.0 (w

) 80.4±0.0 (w

) 87.0 (n)

b16 48.0±1.0 (w

, H=4) 37.5± 0.0 (w

) 38.7±0.0 (w

) 39.4 (w)

b17 31.5±0.8 (w

, H=2) 57.5±3.1 (w

) 28.3±0.0 (w

) 30.1 (w)

b18 57.3±0.0 (w

) 59.2±0.0 (w

, H=6) 58.4±0.0 (w

) 80.8 (w)

s01 42.3±0.4 (w

, H=2) 47.5±2.7 (w

, H=2) 41.8±0.0 (w

) 45.1 (w)

s02 82.8±0.0 (w

) 85.2±0.0 (w

) 82.5±0.0 (w

) 91.9 (w)

s03 33.6±0.0 (w

) 34.6±0.0 (w

) 32.4±0.0 (w

) 37.3 (d)

s04 41.3±0.1 (w

, H=2) 41.4±0.0 (w

) 41.8±0.0 (w

) 48.0 (w)

s05 41.4±0.0 (w

) 41.6±0.0 (w

) 42.0±0.0 (w

) 47.5 (w)

s06 39.6±0.0 (w

) 38.3±0.0 (w

) 38.2±0.0 (w

) 44.1 (w)

s07 45.1±0.0 (w

) 42.8±0.0 (w

) 42.9±0.0 (w

) 51.7 (w)

s08 27.5±0.0 (w

) 28.9±0.0 (w

) 28.3±0.0 (w

) 34.9 (w)

s09 28.6±0.0 (w

) 27.3±0.0 (w

) 28.3±0.0 (w

) 36.5 (w)

s10 35.9±0.5 (w

, H=6) 32.8± 0.0 (w

) 38.6±0.0 (w

) 33.2 (w)

s11 68.4±0.0 (w

) 69.6±0.0 (w

) 71.2±1.2 (w

, H=2) 74.5 (n)

s12 71.8±8.3 (w

, H=4) 69.0±0.0 (w

) 56.7±0.0 (w

) 65.4 (w)

s13 48.1±0.0 (w

) 44.7±0.0 (w

) 47.7 (w)

s14 36.8±0.0 (w

) 43.8±0.0 (w

) 34.0±0.0 (w

) 37.9 (w)

s15 26.5±0.0 (w

) 24.9±0.0 (w

) 23.6±0.0 (w

) 27.2 (w)

s16 33.4±0.0 (w

) 33.8±0.0 (w

) 32.3±0.0 (w

) 36.0 (d)

s17 28.3±0.5 (w

, H=2) 26.7±0.0 (w

) 25.5±0.0 (w

) 32.2 (n)

s18 54.2±0.0 (w

) 53.2±0.0 (w

) 51.9±0.0 (w

) 54.7 (n)

s19 39.8±0.0 (w

) 41.1±0.0 (w

) 40.1±0.0 (w

) 39.9 (w)

s20 64.7±0.2 (w

, H=2) 65.4±0.0 (w

) 61.3±0.0 (w

) 70.7 (d)

s21 34.2±0.3 (w

, H=2) 40.6±0.0 (w

) 32.6±0.0 (w

) 32.9 (w)

bold – statistical signiﬁcance under a pairwise comparison with other NN methods.

underline – best model.

A large number of experiments was conducted, with a total of 39 forecasted links.

Overall, the NN results are quite competitive, outperforming the HW model in all ex-

cept two cases. Regarding the univariate versus multivariate comparison, the results

10 20 30 40 50 60

Traffic (Mbits/s)

Time (x 1 hour)

s03 values

DANN forecasts

10 20 30 40 50 60

Fig.4. Example of the forecasts (left) and observed versus predicted values scatter plot (right).

differ according to the link characteristics. Within the backbone links, the SLNN is the

best option in 10 of the 18 series, while DANN only excels other strategies for one con-

nection (b17 of Figure 1). However, for the core to subnetwork links, the multivariate

DANN strategy provides the best forecasts in 12 of 21 cases, while SLNN achieves the

best performance in only 4 links. These results may be explained by the nature of the

network topology. The core to subnetwork links are peripheral funnels, thus they are

more likely to be inﬂuenced by one single neighbor. In contrast, the core routers are

large carriers, i.e., they direct trafﬁc from/to a larger number of nodes.

Since small networkswere selected,the NNs arevery fast and can be applied in real-

time. Thus, the proposed approach opens room for producing better trafﬁc engineering

tools and methods to detect anomalies in the trafﬁc patterns. This can be achieved with-

out producing any extra trafﬁc in the network and with minimal use of computation

resources, since this work was designed assuming a passive monitoring system.

In future work, the comparison will be extended to other forecasting techniques

(e.g. ARMA models [21]). Moreover, the proposed approach will be applied to trafﬁc

demands of speciﬁc Internet applications, such as Voice over Internet Protocol (VoIP).

Another promising direction is to explore incomplete information scenarios. For in-

stance, to see if it is possible to forecast the backbone link trafﬁc using only the subnet-

work to core connections, i.e., without knowing the past values of the predicted links.

Acknowledgements

This work is supported by the FCT project PTDC/EIA/64541/2006. We would also like

to thank Steve Williams from UKERNA for providing us with part of the data used in

this work.

References

1. K. Papagiannaki, N. Taft, Z. Zhang, and C. Diot. Long-Term Forecasting of Internet Back-

bone Trafﬁc. IEEE Trans. on Neural Networks, 16(5):1110–1124, September 2005.

2. V. Alarcon-Aquino and J. Barria. Multiresolution FIR Neural-Network-Based Learning Al-

gorithm Applied to Network Trafﬁc Prediction. IEEE Trans. on Systems, Man and Cyber-

netics - Part C, 36(2):208–220, 2006.

3. P. Cortez, M. Rio, M. Rocha, and P. Sousa. Internet Trafﬁc Forecasting using Neural Net-

works. In Proceedings of the IEEE 2006 International Joint Conference on Neural Networks,

pages 4942–4949, Vancouver, Canada, 2006.

4. B. Krishnamurthy, S. Sen, Y. Zhang, and Y. Chen. Sketch-based Change Detection: Meth-

ods, Evaluation, and Applications. In Proc. of Internet Measurment Conference (IMC’03),

Miami, USA, October 2003. ACM.

5. J. Jiang and S. Papavassiliou. Detecting Network Attacks in the Internet via Statistical Net-

work Trafﬁc Normality Prediction. Journal of Network and Systems Management, 12:51–72,

2004.

6. S. Makridakis, S. Weelwright, and R. Hyndman. Forecasting: Methods and Applications.

John Wiley & Sons, New York, USA, 1998.

7. G. Reinsel. Elements of Multivariate Time Series Analysis. Springer, San Francisco, CA,

second edition, 2003.

8. A. Lapedes and R. Farber. Non-Linear Signal Processing Using Neural Networks: Prediction

and System Modelling. Tech. Rep. LA-UR-87-2662, Los Alamos National Laboratory, USA,

1987.

9. J. Taylor, L. Menezes, and P. McSharry. A Comparison of Univariate Methods for Fore-

casting Electricity Demand Up to a Day Ahead. Int. Journal of Forecasting, 21(1):1–16,

2006.

10. Q. He, C. Dovrolis, and M. Ammar. On the Predictability of Large Transfer TCPThroughput.

In Proc. of SIGCOMM’05, Philadelphia, USA, August 2005. ACM.

11. H. Tong, C. Li, and J. He. Boosting Feed-Forward Neural Network for Internet Trafﬁc

Prediction. In Proc. of the IEEE 3rd Int. Conf. on Machine Learning and Cybernetics, pages

3129–3134, Shanghai, China, August 2004.

12. T.M. ThomasII. OSPF Network Design Solutions. Cisco Press, 1998.

13. W. Stallings. SNMP, SNMPv2, SNMPv3 and RMON 1 and 2. Addison Wesley, 1999.

14. X. Ding, S. Canu, and T. Denoeux. Neural network based models for forecasting. In Proc.

of Applied Decision Technologies Conf. (ADT’95), pages 243–252, Uxbridge, UK, 1995.

15. I.H. Witten and E. Frank. Data Mining: Practical Machine Learning Tools and Techniques

with Java Implementations. Morgan Kaufmann, San Francisco, CA, second edition, 2005.

16. T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning: Data Mining,

Inference, and Prediction. Springer-Verlag, NY, USA, 2001.

17. W. Venables and B. Ripley. Modern Applied Statistics with S. Springer, 4th edition, 2003.

18. P. Cortez. RMiner: Data Mining with Neural Networks and Support Vector Machines using

R. In R. Rajesh (Ed.), Introduction to Advanced Scientiﬁc Softwares and Toolboxes, IAEng

publishers, Singapore, In Press.

19. R Development Core Team. R: A language and environment for statistical computing. R

Foundation for Statistical Computing, Vienna, Austria, 2007. ISBN 3-900051-00-3.

20. M. Moller. A scaled conjugate gradient algorithm for fast supervised learning. Neural

Networks, 6(4):525–533, 1993.

21. G. Box and G. Jenkins. Time Series Analysis: Forecasting and Control. Holden Day, USA,

1976.