Receptor Response and Soma Leakiness in a Simulated

Spiking Neural Controller for a Robot

David Bowes, Rod Adams, Lola Cañamero, Volker Steuber and Neil Davey

Science and Technology Research Institute, University of Hertfordshire

College Lane, Hatfield, Hertfordhsire, U.K.

Abstract. This paper investigates different models of leakiness for the soma of

a simulated spiking neural controller for a robot exhibiting negative photo-

taxis. It also investigates two models of receptor response to stimulus levels.

The results show that exponential decay of ions across the soma and of a recep-

tor response function where intensity is proportional to intensity is the best

combination for dark seeking behavior.

1 Introduction

In real neural systems it is known that leakiness in individual neurons can be caused

by a variety of physical processes which can in turn lead to a variety of temporal

profiles. Moreover the response of receptors to intensity of stimulus could be either

linear or non linear [7]. Although different mechanisms of leakiness are possible,

some are easier to implement in a robot than others. It is important to identify which

mechanisms will require the least computational effort while producing the desired

behaviour.

In this paper we investigate the effect of the specific function representing leaki-

ness and receptor response, to the ability of an artificial neural system to respond

appropriately to stimulus gradients in order to perform negative photo-taxis.

Photo-taxic robots [6], [4], [5] based on Braitenberg vehicles [3], controlled by ar-

tificial neural networks, have produced both varying results and success [6]. We have

developed a robot controller using a simplified artificial spiking neuron model, im-

plemented in an event driven simulation [8], [2]. The artificial neuron has a leaky

soma which links to an axon hillock. The axon hillock initiates spikes in one or more

collaterals attached to the axon hillock. See Figure 1 for an illustration of the artificial

spiking neuron.

Using a modified Braitenberg fear vehicle [3], we simulated the behaviour of

negative photo-taxis. In the original Braitenberg fear vehicle the output of the left

light sensor is used to set the power output on the left motor, and a corresponding

arrangement is made on the right side of the vehicle. In our modified arrangement we

add sensory neurons, connected to interneurons, which then connect to the motor.

This gives a potentially wider range of behaviours. However this arrangement was

only satisfactory when the light intensity difference between the two light sensors was

Bowes D., Adams R., Cañamero L., Steuber V. and Davey N. (2008).

Receptor Response and Soma Leakiness in a Simulated Spiking Neural Controller for a Robot.

In Proceedings of the 4th International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 100-106

DOI: 10.5220/0001509001000106

 SciTePress

large. When the differences were not large, the robot was unable to correctly orientate

itself towards darkness.

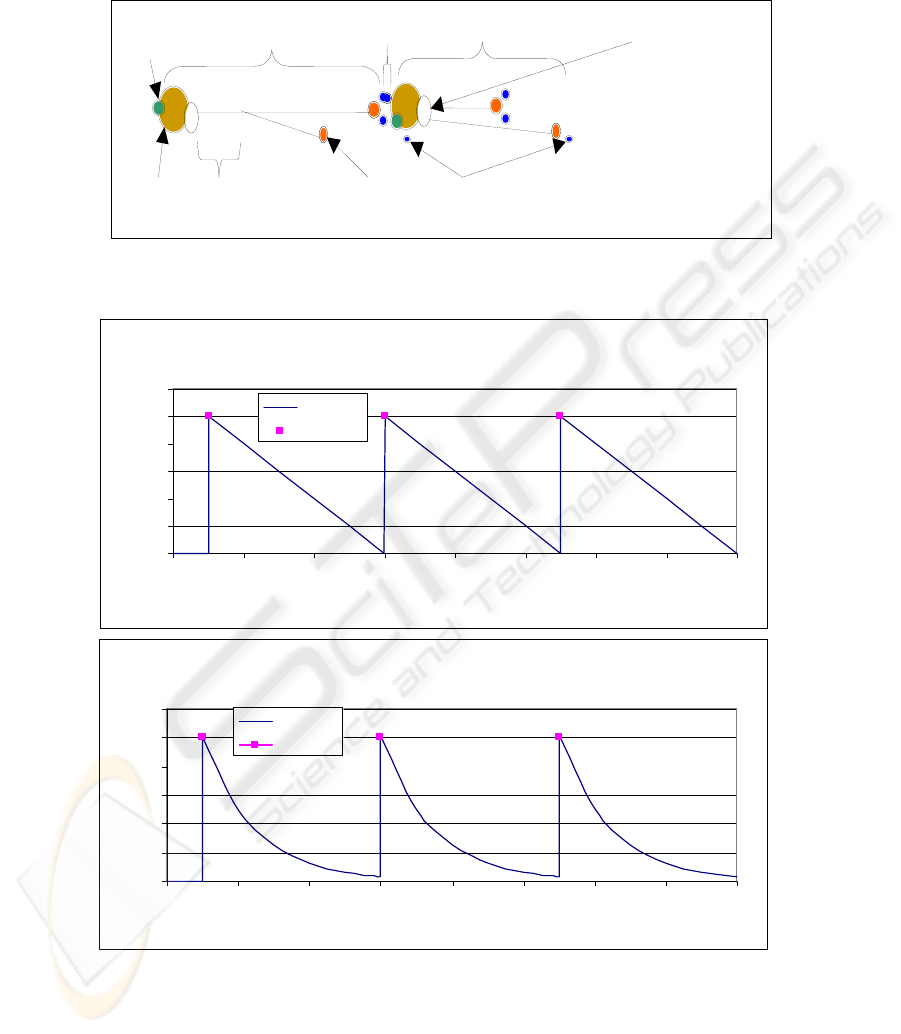
Fig. 1. The model of a simplified spiking neuron showing soma, axons, chemical receptor,

synapse and neurotransmitter (note that the dendritic tree is not modeled).

Linear Decay

0246810121416

Time

Potential

Addition

Exponential Decay

0 2 4 6 8 10 12 14 16

Time

Potential

Addition

Fig. 2. Membrane potential with different decay functions with a constant rate of voltage addi-

tions generated by the arrival of spike events (designated by Addition points in the graph).

Chemi-

receptor

euron

Synapse

Soma

Axo

tic bouton

Neurotransmitter

Neuro 2

Axon hillock

101

Two aspects of the model that could account for this lack of sensitivity were thought

to be: the nature of the leakiness of the soma and the relationship between light inten-

sity and firing rate of the light receptors.

In real neurons leakiness is controlled by a variety of mechanisms including volt-

age dependent and independent ion channels, active transport though pumps, ex-

changes and axial currents [7].

Subsequently we studied two models for leakiness: linear decay in voltage, which

simple, and an exponential decay which is more plausible and could be caused by

ions passing through pores along a concentration gradient, see Figure 2.

Both of these are biologically possible, but the latter system, which does not involve

the direct use of energy, is more likely in a biological organism where parsimony of

design is often found.

The relationship between light intensity and input current to a receptor neuron is

complex and may lead to a variety of mappings between light intensity and the firing

rate of a receptor.

To investigate this, two models for firing rate of a receptor cell, under different

light intensities, were studied: inter spike time being inversely proportional to light

intensity, or, inter spike time being proportional to the difference between the maxi-

mum possible intensity and actual intensity. The first of these produces a linear rela-

tionship between light intensity and firing rate and the second produces a hyperbolic

relationship. Both of these are biologically plausible [7]. The first model would result

in firing rate being proportional to light intensity and the second method would pro-

duce a non-linear relationship as shown in Figure 3.

Firing rate v Light intensity

0 20406080100

Light intensity as percentage of max

Firing rate (spikes/s)

Inverse inter spike time

Linear inter spike time

Fig. 3. Firing rates of the sensory neuron using a linear and hyperbolic relation. Note the poor

discrimination of the hyperbolic function at low light intensities.).

102

2 Methodology

The experiment to test which function produced the greatest rotation was carried out

on a robot, simulated in software. A schematic of the robot is shown in Figure 4.

Fig. 4. A schematic of the robot indicating the position of the two light sensors and two in-

terneurons which attach to the motors. Note the connections are excitatory which causes the

vehicle to perform negative photo-taxis.

Simulated receptor neurons were attached to light sensors. These sensory neurons

then connected to interneurons which subsequently attached to the motors with exci-

tatory ipsilateral connections (left receptor connects to left motor). At the start of each

experiment the robot was placed perpendicular to a linear light gradient, see Figure 5.

0 Distance from black : Proportional to light intensity : Arbitrary units 10000

Fig. 5. The Robot on the linear light gradient. The robot is placed orthogonally to the gradient

and is “pinned” in position so that it can only rotate (X marks the vertical axis of rotation).

The simulation prevented forward motion of the robot, but allowed rotation so that

the robot would spin on the spot (similar to an insect being tested for pheromone

orientation in a wind tunnel). The simulation was run for 10 seconds and the total

ht sensors

Moto

Wheels

Driven together

Bumper

Inter neuron

103

angle of rotation was recorded. The robot was placed at incremental distances from

the left side of the gradient, providing 9 data samples. Each permutation of decay

model, receptor firing model and position was repeated 7 times, resulting in a total of

252 experiments.

The two models for potential decay in the soma of the interneuron are:

• Linear decay: which is very simple to calculate

−=

+ tt

)1(

• Exponential decay: biologically more plausible

cc =

+ )1(

Where c is the synaptic concentration with constants α and β, where β < 1.

Two models for determining the time between firings of light receptor neurons

were:

• Inverse

min

T +∝

∝

producing a linear relationship between light intensity and neuron firing rate.

• Linear

(

)

min

TikT

−

∝

−

∝

producing a hyperbolic relationship between light intensity and firing rate.

Where k is the maximum stimulus level achievable, i is the intensity of stimulation

F is the firing rate and

min

is a constant which prevents the period being less than

0.01s (below this value the amount of processing increases significantly).

3 Results

The full results for all four experimental conditions are given in Figure 6. This shows

that significant rotation only occurs under the condition of exponential voltage decay

and inverse inter spike time and then only in the dark region.

A study of the motor logs for all conditions indicated that at high light levels, both

motors had been turned on to the maximum level due to very high rates of input fir-

ings. This had occurred because the soma of the interneuron had saturated and had

prevented the voltage dropping below the threshold value for spiking.

104

Amount of rotation for different light intensities

-0.2

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

0 1000 2000 3000 4000 5000 6000 7000 8000 9000

Distance from Black ( proportional to light intensity)

Accumulated angle of rotation (radians

)

Exp Decay, Inverse Inter Spike Time

Exp Decay, Linear Inter Spike Time

Linear Decay, Inverse Inter Spike Time

Linear Decay, Linear Inter Spike Time

Fig. 6. A graph of the amount of rotation achieved. This shows the results for the four condi-

tions: exponential voltage decay and inverse inter spike time, exponential voltage decay and

linear inter spike time, linear voltage decay and inverse inter spike time, and linear decay and

linear inter spike time. The exponential voltage decay and inverse inter spike time is the only

configuration where significant rotation occurred.

Linear decay of potential performed particularly poorly. In high light intensity the

decay of voltage in the interneuron was not sufficient to allow the voltage to fall be-

low the firing threshold – the rate of decay in this model is constant and is therefore

not related to the actual voltage. Moreover at low light intensities the voltage decay

was too rapid to allow the voltage to ever exceed the firing threshold. Exponential

decay of potential was much better: in this case the rate of decay is proportional to

voltage, producing much greater sensitivity at the interneuron.

As already noted a linear relationship between inter spike times and light intensity

at the light receptor neurons gives rise to a hyperbolic relationship between intensity

and firing rate. This gives poor discrimination at low light levels and the results dem-

onstrate the inadequacy of this encoding.

4 Discussion

In real neural systems it is known that leakiness in individual neurons can be caused

by a variety of physical processes, which can lead to a variety of temporal voltage

profiles. Moreover the response of receptors to intensity of stimulus could be either

linear or non linear [7].

Our results show that for the example of a negatively photo-taxic robot, an expo-

nential decay of membrane potential and an inverse relationship between light inten-

105

sity and inter spike time (resulting in a linear relationship between light intensity and

firing rate) produces the greatest rotation at low light levels.

At high light levels the rotation is limited due to both motors being stimulated at

the maximum rate because the interneurons receive levels of stimulus which prevents

the membrane potential from dropping below threshold.

Interestingly, the most effective neural model is also the most biologically plausi-

ble. Diffusion of ions through pores would naturally give rise to an exponential decay

whereas linearization of the decay would require additional voltage dependant mecha-

nisms.

The modified Braitenberg wiring using interneurons is biologically more realistic

than the original vehicle because it involves some level of processing by the interneu-

rons, but it is not sophisticated enough to cope with the full range of light levels. We

are currently investigating models of dynamic normalisation to achieve greater sensi-

tivity to small differences in light intensity.

References

1. Hodgkin, A. L. and Huxley, A. F: A quantitative description of ion currents and its applica-

tions to conduction and excitation in nerve membranes. J. Physiol. (Lond.), 117:500-544.

(1952).

2. Bowes,D.H; Adams,R.G; Cañamero,L; Davey,N: “A Simplified Spiking Neural Network

for a Robot” Technical report, Science and Technology Research Institute, University of

Hertfordshire (2007)

3. Braitenberg V: Vehicles: experiments in synthetic psychology. Elliot Sober (1984)

4. Floreano D: Evolutionary Robotics:A Short Tutorial (2005)

5. French, R.L.B.; Cañamero, L., "Introducing Neuromodulation to a Braitenberg Vehicle,"

Robotics and Automation, 2005. ICRA 2005. Proceedings of the 2005 IEEE International

Conference on , vol., no., pp. 4188-4193, 18-22 April (2005)

6. Bisset, D. L.; Vandenbergh, R. C: The Dynamics of Photo- Taxis: Applying the Agent

Environment Interaction System to a Simple Braitenberg Robot European Conference on

Artificial Life Vol 4, 327-336 (1997)

7. Kandel ER, Schwartz JH, Jessell TM: Principles of Neural Science, 4th ed. McGraw-Hill,

New York (2000)

8. Rochel, O; Martinez, D: An event-driven framework for the simulation of networks of

spiking neurons, European Symposium in Artificial Neural Networks, pp 295-300 (2003)

9. GM Sheperd: The Synaptic Organization of the Brain, 5thRev, Oxford UP ,New

York.(2004)

106