
Intelligent
Refueling Advisory System
Erica Klampfl
1
, Oleg Gusikhin
1
, Kacie Theisen
1
, Yimin Liu
1
and T. J. Giuli
2
1
Ford Research & Advanced Engineering, Systems Analytics & Environmental Sciences
Department, RIC Bldg, MD #2122, 2101 Village Rd., Dearborn, MI 48124, U.S.A.
2
Ford Research & Advanced Engineering, Vehicle Design & Infotronics Department
RIC Bldg, MD #3137, 2101 Village Rd., Dearborn, MI 48124, U.S.A.
Abstract. Recent advances in wireless communication technologies have led to
numerous new developments that take advantage of network access, ranging from
real-time information delivery essential for many driving decisions to harvesting
off-board computing power for remote vehicle diagnostics. Specifically, with the
ever increasing fuel cost, there is growing popularity of services that provide
information to drivers on current gas prices and alerts on upcoming changes to
gas prices. This paper demonstrates how to take currently available technology
one step further by providing a proactive refueling advisory system based on
minimizing fuel costs over routes and time. The system integrates vehicle data, a
navigation system, and internet connectivity to supplant the existing vehicle low
fuel warning with a comprehensive decision support system on refueling choices.
1 Introduction
Recent advances in wireless communication technologies have led to numerous devel-
opments that take advantage of internet connectivity. These developments support a
wide range of industries and applications. Focusing on the personal transportation sec-
tor, harvesting computing power accessible over the net can be used for remote vehicle
diagnostics. Another example is real-time information delivery used onboard vehicles
to assist drivers with decisions such as where to find the nearest gas station. A popu-
lar extension of this is an emerging service that offers access to current retail gasoline
prices. With ever increasing fuel prices, drivers are paying closer attention to their re-
fueling strategies, making when and where to refuel a more important and complex
question than in the past. Many drivers are willing to drive a few extra miles to get a
cheaper gas price. Drivers may even be willing to only purchase a few gallons of gas
today when refueling is necessary with expectations of lower gas prices the next day;
this results in more frequent stops, but lower total fuel costs.
The model we introduce in this paper offers users substantial benefits by identifying
the best possible refueling strategy over an entire route and multiple time periods, as
opposed to the best strategy based on current gas prices in a small local area. It includes
how to determine the best refueling strategy for a driver by considering their route, the
gas stations and gas prices along the route, the starting fuel level, good estimates of fuel
consumption along the route, and user preferences.
Klampfl E., Gusikhin O., Theisen K., Liu Y. and J. Giuli T. (2008).
Intelligent Refueling Advisory System.
In Proceedings of the 2nd International Workshop on Intelligent Vehicle Control Systems, pages 60-72
Copyright
c
SciTePress

Inputs to the system can come from several different sources. A driver’s route can
be determined in either of two ways: it can be manually input or for frequently driven
routes it can be predicted from past driving patterns (see [8] and [16]). Once the route
has been determined, gas stations along the route can be identified along with current
gas prices. Current gasoline prices can also be used to estimate future fuel prices by a
forecasting model. By connecting to the vehicle’s internal network, the current fuel level
can be obtained along with the vehicle’s average fuel economy, which can be used to
form a good estimate of fuel consumption for new routes. For frequently driven routes,
previously collected data from the vehicle internal network can be used determine route
specific fuel consumption.
We will first present background in Section 2 and then give an overview of our
system in Section 3. We then provide details on how we forecast future gas prices
and determine the refueling strategy in Sections 4 and 5, respectively. We present an
example in Section 6 and discuss future work and conclude in Section 7.
2 Background
In the United States, there are currently two main sources of current gasoline prices:
credit card transactions and networks of gas price spotters. GasBuddy [10] and GasPrice-
Watch [11] are examples of the latter approach. Both companies offer a web site and
mobile application where the user can look up gas prices for free. The gas prices re-
ported are collected from a network of gas price spotters who are usually volunteers.
Consequently, neither company can guarantee the accuracy of the information they pro-
vide. Oil Price Information Services (OPIS) [19] obtains their data from credit card
transactions, which makes it more reliable than other sources.
When a driver is deciding whether or not to stop to purchase gas, they usually con-
template if the gas prices will be going up or down in the next couple of days. Gas
prices at the pump largely depend on wholesale prices and are subject to cyclical fluc-
tuations. While some people follow fluctuations of retail gasoline prices and may have
reasonable predictions on when prices will rise or fall, the majority of drivers do not
know the likelihood of gas prices going up or down. There are a number of popular web
sites that offer the general population an educated guess on the future direction of gas
prices; one example is The Gas Game [20].
To assist drivers in making more informed refueling decisions, many car navigation
system manufacturers offer gas price services delivered to the vehicle through mobile
phone data services or satellite radio broadcast. Examples include the TomTom 920T
[17], Dash express [3], and n
¨
uvi 780 by Garmin [9] (most get their prices from OPIS).
Vehicle manufacturers, like Ford Motor Company, are even taking this one step fur-
ther by offering their factory installed navigation system with SIRIUS Travel Link [7].
In addition, some researchers have explored notifying drivers of the cheapest place to
refuel when their current gas level drops below a certain threshold (see [13] and [15]).
In comparison to the privately owned vehicle sector, the commercial trucking in-
dustry has considered complex decisions about when and where truck drivers should
stop for gas as a part of their route planning process for quite some time due to the tight
correlation between profits and fuel cost. They have developed optimization models to
61
assist with refueling decisions as each truck’s driving route is known and network in-
frastructures are in place to communicate with truck drivers on the road: an example is
Expert Fuel developed by Integrated Decision Support [14].
Our approach differs from the above in the several ways. First, we use forecasted
gas prices, so that we can consider future days on the route, making the best decision
over multiple days. While forecasting has been used for other consumer oriented help
applications, such as predicting when online customers should purchase airline tickets
[6], it is a new approach for providing refueling strategies. Another way that our ap-
proach is different is that our routes do not have to be predetermined, as we can get
routes directly from the vehicle GPS. In addition, we get other data directly from the
vehicle internal network, such as current fuel level and fuel consumption. Also, we can
recalculate on the fly a new strategy if the driver deviates from the original plan. Fi-
nally, our system acts as a proactive fuel gauge that notifies the driver before they are
approaching the gas station where they should stop (current low on fuel gauge warnings
provide data only relative to the internal fuel tank).
3 System Overview
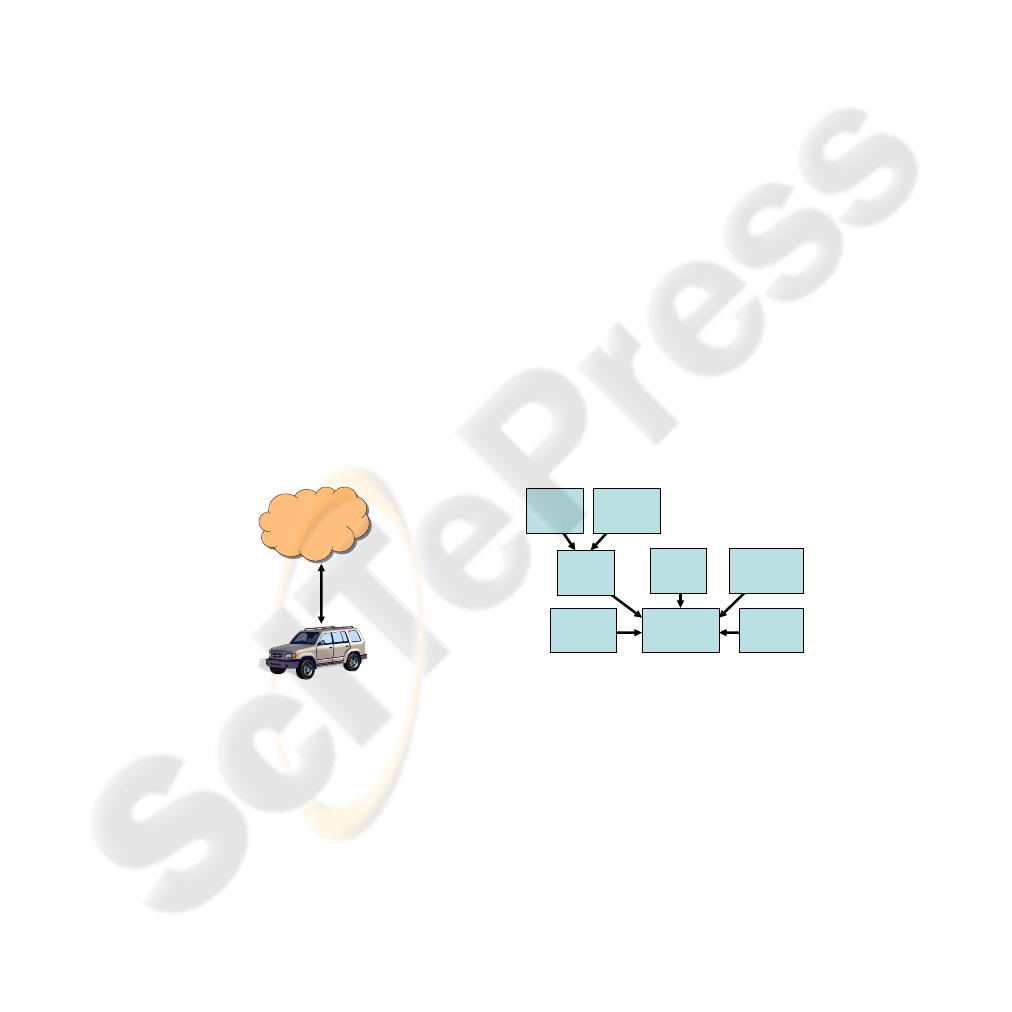
Our system combines web and in-vehicle components to assist the driver in minimizing
their fuel purchase costs, as seen in Figure 1. To use the system, a driver must first reg-
ister on a web portal and enter their fuel purchase preferences, such as how many times
per week they are willing to stop for gas and which brands they prefer. The web site
also assists the driver in mapping out their frequently traveled routes. The driver then
creates an approximate travel plan for the next week, which the system uses to identify
potential refueling stations. Future versions of our system will predict the driver’s future
driving routes without any input from the driver
Web server
Fig.1. System consisting of web to vehicle con-
nection.
Current
price
Historical
prices
User
preferences
Predicted
prices
Refueling
optimization
Vehicle
route
Wholesale
prices
Current
fuel level
Fig.2. This figure illustrates the data
flow used in the refueling strategy op-
timization algorithm.
To get the most out of our system, the driver’s vehicle should include a navigation
system and a means of connecting the vehicle to the internet, such as a telematics plat-
form (e.g., OnStar [18], BMW Assist [1]) or a cell phone with data service (e.g. GPRS
or EVDO). The vehicle maintains a connection to the web server and periodically up-
loads the vehicle’s current fuel level and GPS location. An optimization algorithm (see
Section 5.1) on the web server uses the fuel level to calculate when and where the driver
62

should refuel and how many gallons to purchase. If the algorithm determines that the
driver should stop, it sends this information to the vehicle’s navigation system and alerts
the driver.
Figure 2 shows the main data sources our system uses to calculate a refueling plan.
Future fuel prices for individual fueling stations are predicted using a forecasting al-
gorithm (see Section 4) that takes into account historical prices as well as wholesale
prices. Historical and current prices are obtained from a database maintained by OPIS.
User preferences and vehicle routes are obtained from the web portal, and the current
fuel level is directly obtained from the vehicle.
4 Forecasting Model
As previously mentioned, if the consumer had more information on gasoline prices at
each gas station along the specified route and predicted prices for the next few days,
determining a refueling plan that would minimize the total fuel cost over the trip would
be achievable. One important aspect in determining the consumer’s refueling strategy
is an econometrical model that reasonably predicts daily gasoline retail prices at each
station on the route. Many studies show that the retail gasoline price is highly correlated
with wholesale gasoline price, according to the production and distribution system of
gasoline in the U.S [2]; this provides the foundation for our approach.
We present a simple forecasting approach that predicts future retail gas prices at
individual stations when the following limited data is available: wholesale regional gas
prices, one-month future market wholesale prices, current station retail gas prices, and
historical retail station gas prices. To determine which wholesale price to use as the
explanatory variable in our forecasting model, we considered several wholesale prices
to see which provided the best correlation to retail gas prices. There are four regional
wholesale prices in the U.S.: mid-continent, Los Angeles, New York, and Gulf coast
markets. These four regions and the one-month future market wholesale prices have
the following correlation with retail prices at gasoline stations in Michigan: 0.89, -0.71,
-0.89, 0.92, and -0.91, respectively. In addition, we tested the correlations between the
average of two or more wholesale prices and the retail gasoline prices: all values were
less than 0.92. As a result, we chose the Gulf coast wholesale price as our explanatory
variables in the model, which yielded the best correlation to retail gas prices.
The Energy Information Administration (EIA) reported in 1999 [5] that the down-
stream gasoline price responses caused by upstream price changes can be represented
by the following equation:
D
t
= β
0
+
X
i
(β
i
U
t−i
) + ε. (1)
Here D
t
is the price offered to each gas station by the supplier at time t; it is a moving
average of the wholesale prices U
t−i
at time t for the previous days i such that i =
1, . . . , 6. The error term is ε, which also represents the downstream markup.
The markup of each gasoline station π
t
at time t is the retail gasoline price p
t
at
time t at each gasoline station minus the price D
t
paid to its suppliers; that is,
π
t
= p
t
− D
t
. (2)
63
In this study, we do not use the coefficients β provided by the EIA report, but esti-
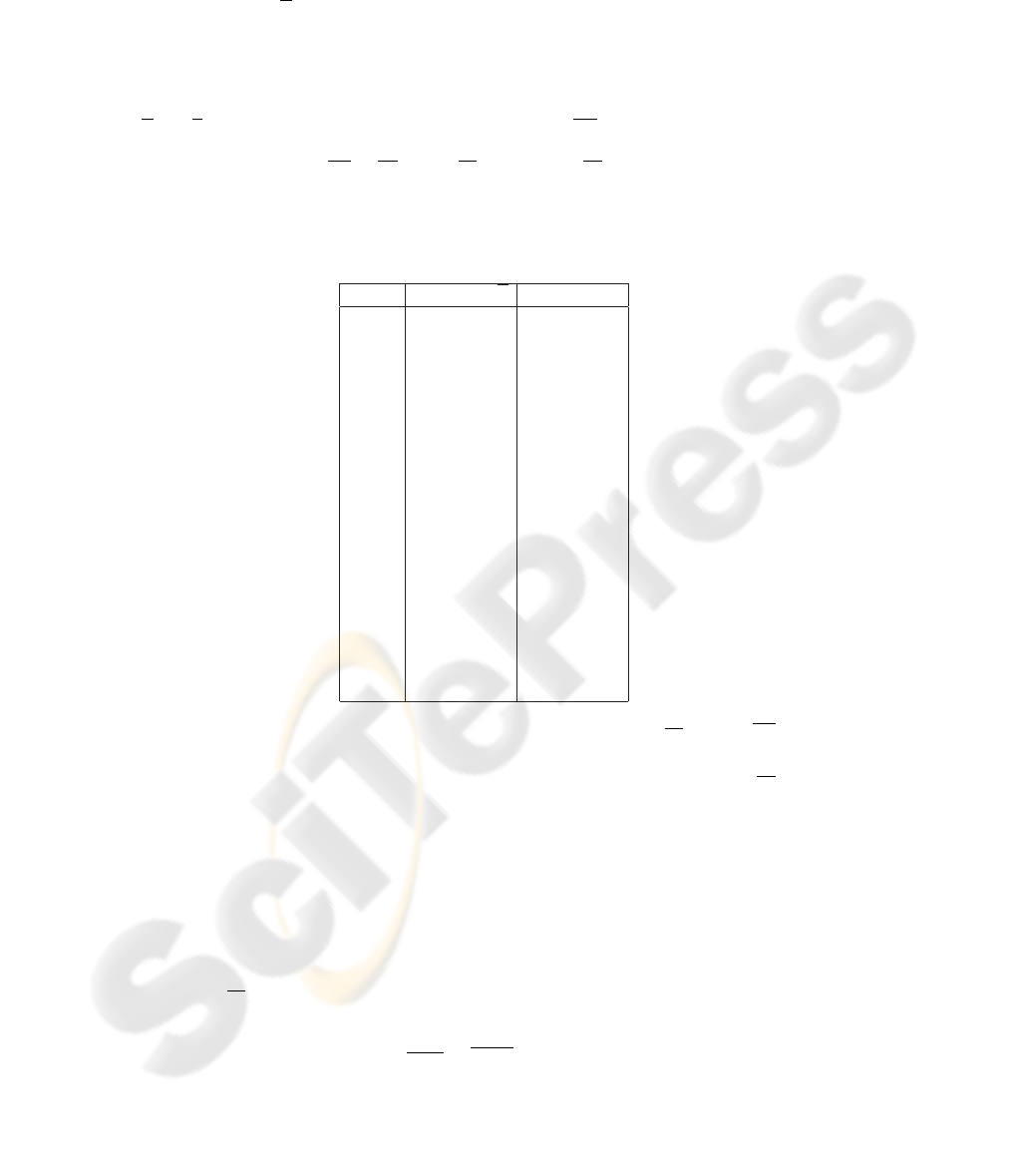
mate coefficients β by applying an Ordinary Least Square (OLS) linear regression [12]:
the retail gasoline price at time t is the dependent variable, and explanatory variables are
the wholesale prices U
t−i
for i = 1, . . . , 6, and the monthly dummy prices, M
k
, where
k = 1, . . . , 12 represents January through December, respectively, for any day t. The
results of this OLS linear regression are in Table 1. Applying the regression coefficients,
β and θ, we can obtain the estimated suppliers’ prices D
t
:
D
t
= β
0
+
X
i
(β
i
U
t−i
) +
X
k
(θ
k
M
k
). (3)
Table 1. Relationship between retail gas and mid-continent wholesale prices: R
2
= 0.97, ***Sta-
tistically significant at 99% confidence level, *Statistically significant at 90% confidence level.
Variable Coefficient (β) Standard Error
U
t−1
0.002 *** 0.001
U
t−2
0.001 0.001
U
t−3
0.001 0.001
U
t−4
0.001 0.001
U
t−5
4.531 e-04 0.001
U
t−6
0.003*** 0.001
M
2
-0.180 *** 0.014
M
3
-0.090*** 0.020
M
4
-0.039* 0.031
M
5
0.020 0.038
M
6
0.089*** 0.033
M
7
0.088*** 0.032
M
8
0.102 *** 0.025
M
9
-0.012 0.030
M
10
-0.012 0.030
M
11
0.001 0.041
M
12
0.009* 0.006
constant 0.950*** 0.059
So, the estimated markup of each gasoline station at time t is π
t
= p
t
− D
t
. How-
ever, we randomly chose some gasoline stations to study their markup and found some
interesting markup patterns. For each day of the week, even if the markup π
t
is dif-
ferent for every t, it is always higher at the end of a week and lower at the beginning
of a week. Since it is not feasible to test each gasoline station’s markup, we make the
assumption from our comprehensive testing that gasoline prices at each gasoline station
have a weekly pattern; without loss of generalization, we calculate the average markup
for each weekday, providing us with seven average markups for each gasoline station.
We call this average markup for each weekday ˜π
n
for n = 1, . . . , 7; i.e. for each day
of the week n, we calculate the average markup for n using historical data for n. For
example, to calculate ˜π
n
for n = 1 (Monday), we take the average markup over all
Mondays (π
t
such that t is a Monday) in our historical data. Hence, we can predict the
gas price for any station one day in advance by
p
t+1
= D
t+1
+ ˜π
n
, (4)
64

where n = 1, . . . , 7 represents Monday through Sunday, respectively, for any day t.
When retail gas price for time t is not available for a specific station, we can also use
equation (4) to estimate the missing price.
To forecast the gasoline prices at one specific gasoline station more than one day
in advance, we can do so using p
t+i
= D
t+1
+ ˜π
n+i
, for i = 1 to m, where m is the
number of days ahead for which the forecast is desired. Because we do not know the
wholesale or suppliers’ prices on days t+i, when i > 1, the accuracy of the forecasting
results will decrease as i increases.
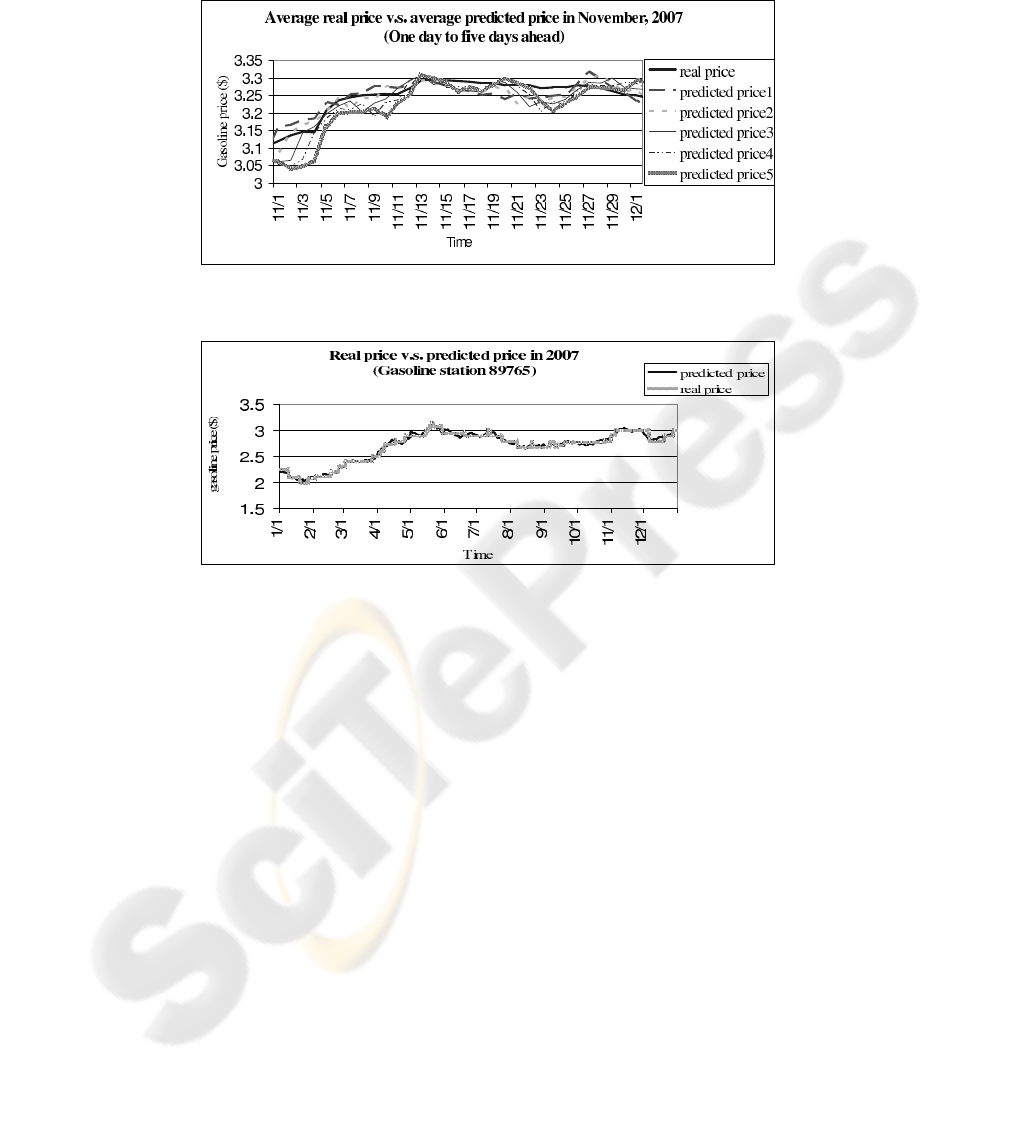
The graphs below show the prediction results from the simple price forecasting
model described above for gas purchases using 2007 daily data. Figure 3 and 4 dis-
play average daily retail gasoline prices (averages include prices for 931 stations) and
predicted gasoline prices in Michigan. Figure 3 shows the average daily retail gasoline
prices compared to the predicted gasoline prices based on the one-day ahead predic-
tion for Michigan over 2007. Figure 4 includes five predicted prices which are one-day
ahead, two-day ahead, three-day ahead, four-day ahead and five-day ahead, respectively,
for the month of November 2007. For example, when using the three-day ahead predic-
tions, we would use November 1, 2007 data to predict the price of gas on November 4,
2007. The mean of absolute residual values (i.e., the absolute difference between real
price and predicted price) for the one to five day ahead predictions are approximately
3.2 cents, 2.8 cents, 2.9 cents, 3.1 cents, and 3.3 cents; the standard deviation of the
absolute residual values is 2.3 cents, 2 cents, 2.1 cents, 2.2 cents and 2.4 cents, respec-
tively. Figure 5 show the predicted daily gasoline prices at one stations in Michigan as
an example to demonstrate the accuracy of predicted prices for an individual gas station.
Fig.3. Average retail price compared to average predicted retail price for 931 gasoline stations.
Some papers discuss factors that impact daily or weekly gasoline price fluctuation
[4], but few researchers have studied forecasting models for daily gasoline prices. Com-
pared to those models, our approach for price prediction provides a simple way when
limited data is available to estimate daily gasoline price at each gasoline station with
forecasting results that are within a reasonable range to the retail prices. In future re-
search, we plan to develop a more advanced forecasting model that will require more
data, but will be able to include effects of other factors on retail gasoline prices, such
as a gasoline station’s brand, distance to competitors, station characteristics, regional
income level, etc. Moreover, we will use an autoregressive integrated moving average
65
(ARIMA) model [12] to better understand the lag terms t−i (the number of days before
t that are considered) and their coefficients.
Fig.4. Average retail price and 5 average predicted prices of 931 stations in November, 2007.
Fig.5. Real retail price and predicted retail price at gasoline station 89765 in 2007
5 Solution Techniques
Once we have the forecasted gas prices, we are ready to use these as cost inputs to
the objective function in our optimization model. There are a number of different ap-
proaches for solving the optimal refueling strategy problem from heuristical approaches
to discrete optimization methods. In this paper, we first describe how to model the re-
fueling strategy optimization problem as a Mixed Integer Program (MIP) [21]. Next,
we briefly explore two simple heuristics: the first has the driver stop at the cheapest gas
station in the area whenever the driver runs out of gas, and the second recommends a
refueling stop within a certain tank capacity range.
5.1 Mixed Integer Program
We first describe the MIP optimization technique, introducing the input information,
discussing the variables, the objective function, and ending with a detailed description
of the constraints and overall model formulation.
66

Input Information. In this section, we describe the parameters that are inputs to the
MIP model. We divide these inputs into the following categories: inputs obtained from
vehicle internal network, inputs implicit from route specifications, inputs defined by
user to specify preferences, and inputs from the forecasting model. We define a route to
be a multi-day trip plan of around one week. After a week, the accuracy of the forecasted
gas prices diminishes. However, the week can be a rolling horizon, where the model is
solved every day for a new week time period.
We get the following information from the vehicle internal network:
Max = maximum number of gallons the gas tank holds
MPG = miles per gallon (note that this could be different depending on the route)
G
0
= initial amount of gas in the vehicle at the beginning of the route
As discussed in Section 3, driver routes are continually being collected on the vehicle
internal network to populate the user’s most frequently driven routes or can be set up
on the web portal by the driver for routes not previously driven.
Knowing these routes, we can determine the following inputs:
n = number of gas stations in route
S = set of gas stations in route = {1, 2, . . . , n}
m = number of driving days or time periods in the route
D = set of days = {1, 2, . . . , m}
d
i
= the distance from the starting point of the route to gas station i
ξ
i
= the distance from each station i back to the original route
NP I
t
= the new period index ∀ t ∈ D. The gas stations are sorted in the order in
which the driver will encounter them along the route. NP I
t
identifies the
first gas station encountered on day t. For example, N P I
1
= 1 is the index
for the first gas station in the first time period. If on the second day (t = 2)
the first gas station to visit is station 256, then NP I
2
= 256.
In addition to the routes, the user specifies the following preferences through the
web portal:
Min = minimum number of gallons of gas the driver wants to have in the fuel tank
at any given time
MST = maximum number of stops over the entire route (note that this
should take into consideration the number of miles driven so that the
problem does not become infeasible)
MSD = maximum number of stops in one day of the trip (note that this
should take into consideration the number of miles driven so that the
problem does not become infeasible)
The last input involves the cost of gas at each station. If the gas station occurs along
the route on the current day, then the cost of gas is the current gas price. If the gas
station occurs along the route on a future day or the current day’s price is not available,
then it comes from the forecasting model.
c
i
= cost of gas at station i.
We keep track of the first station in each time period, so we get the corresponding
forecasted gas prices p
t+i−1
for days i = 2, . . . , m for each station.
67

Variables. This model contains both binary and continuous variables. The binary vari-
ables help make choices of when to stop, whereas the continuous variables determine
how much gas to get at a station.
– The first variable, x
i
, is a binary variable that determines whether or not the driver
should stop at gas station i. In other words,
x
i
=
½
1 if stop at gas station i
0 otherwise
∀i ∈ S.
Recall that the time period is embedded in this variable as we keep track of it by
the value NP I
t
.
– The second variable, y
i
, is the amount (in gallons) of gas purchased from station i
for every i ∈ S.
Objective Function. The objective is to minimize the total amount spent on gas when
traveling on a specific route over a certain number of days. The user preferences of how
many times they are willing to stop also comes into play by adding a weighted penalty
to the number of stops. If the user does not set a preference for the number of stops, then
we let α = 0; that is, we don’t impose a penalty. The objective function is as follows
min
X
i
(c
i
y
i
+ αx
i
) (5)
Constraints. In this section, we will discuss the constraints that are involved in guar-
anteeing that the driver does not run out of gas, that the driver does not get more gas
than the fuel tank can hold, and if the driver stops at a station than the driver must get
gas.
The first constraint specifies that the vehicle must never run out of gas. So, when the
vehicle gets to station i, the amount of gas that the vehicle had at station i −1 needs to
be enough to get to station i and still have the minimum gallons required. Note that we
add the distance ξ
j
to account for the distance that the driver takes if they stop at some
station j < i to get back to their route.
Min ≤ G
0
−
d
i
MP G
+
X
j<i
y
j
−
X
j<i
ξ
j
MP G
x
j
∀ i ∈ S. (6)
The second constraint guarantees that the vehicle will never have more gas than the
amount held by the fuel tank. So, for every station visited,
G
0
−
d
i
MP G
+
X
j≤i
y
j
−
X
j<i
ξ
j
MP G
x
j
≤ Max ∀ i ∈ S. (7)
We also constrain the number of stops per route; this accounts for how much gas the
vehicle’s tank can hold so that the problem does not become infeasible.
X
i∈S
x
i
≤ M ST (8)
68

Or, if we only want a maximum number of stops per day, we address it by the
following two constraints. The first constraint is for all time periods except for the last
one, and the second constraint covers the last time period:
X
i∈S:i≥NP I
t−1
&i<NP I
t
x
i
≤ M SD ∀ t ∈ D \1,
X
i∈S:i≥NP I
m
&i≤n
x
i
≤ M SD. (9)
The last two constraints are linking constraints that guarantee if the driver does not
stop at station i to get gas then no gallons should be purchased; that is,
y
i
≤ (Max −Min)x
i
∀ i ∈ S and x
i
≤ y
i
∀ i ∈ S. (10)
Bounds. The variable x
i
is a binary variable. The variable y
i
is a real number that must
be greater than or equal to zero, but less than or equal to the size of the fuel tank minus
the preference of how much fuel should always be left in the tank. Note that the upper
bound on the y
i
variable is implied by the first linking constraint in (10). The bounds
are as follows: x
i
∈ B ∀ i ∈ S and 0 ≤ y
i
≤ Max −Min such that y
i
∈ < ∀ i ∈ S.
Problem Formulation.
min
x
i
, y
i
∀i ∈ S
X
i
(c
i
y
i
+ αx
i
)
s.t.
Min ≤ G
0
−
d
i
MP G
+
P
j<i
y
j
−
P
j<i
ξ
j
MP G
x
j
∀ i ∈ S
G
0
−
d
i
MP G
+
P
j≤i
y
j
−
P
j<i
ξ
j
MP G
x
j
≤ Max ∀ i ∈ S
P
i∈S
x
i
≤ M ST
P
i∈S:i≥NP I
t−1
&i<NP I
t
x
i
≤ M SD ∀ t ∈ D \ 1
P
i∈S:i≥NP I
m
&i≤n
x
i
≤ M SD
y
i
≤ (Max −Min)x
i
∀ i ∈ S and x
i
≤ y
i
∀ i ∈ S
x
i
∈ B ∀ i ∈ S and 0 ≤ y
i
≤ Max −Min
5.2 Heuristics
Two different heuristic approaches are considered as possible solution techniques. The
first approach has the driver stop for gas whenever the fuel gage hits a minimum allow-
able fuel level. For example, if this minimum level is 2 gallons then the driver will stop
at the gas station right before the fuel level drops to 2 gallons. When stoping for gas
the driver always refuels to the maximum tank capacity. This method may not give the
lowest total fuel cost over a trip, however it will result in the minimum number of stops
possible to complete the trip. The second method is a Greedy heuristic where the driver
continues along their given route until the fuel gage registers a predetermined amount.
As an example, let this predetermined amount be half a tank of gas. At this point, the
heuristic checks all of the given gas stations between half a tank and the minimum al-
lowable fuel level. The station with the lowest gas price in this range is selected as the
69

refueling point, and when the driver stops, they fill their tank to the maximum capac-
ity. The driver then continues along the route until the fuel level reaches half a tank,
at which point the process repeats itself. This method should show some improvement
in fuel costs compared with the previous heuristic and will eliminate the possibility of
purchasing small amounts of gas at any given stop.
6 Example Scenario
A sample scenario was created to demonstrate the various solution techniques and to
compare resulting MIP solutions when user preferences are considered. In this scenario,
a five day trip has been planned in which there are 1532 possible gas stations to stop at
along the route. For each gas station, the forecasted price of gas and the distance from
the starting point is known. The driver’s vehicle averages 22 miles per gallon, holds a
maximum 15 gallons of gas, and is starting the trip with 5 gallons of fuel. The driver
preferences are not to let the fuel level drop below 2 gallons and no stopping for gas
more than twice in one day or more than six times over the entire trip.
Table 2. Scenario Results for Optimization Methods.
Optimization Optimization with Penalty
Day ID Distance Price ($) Buy Day ID Distance Price ($) Buy
1 28 15.571 2.799 10.708 1 41 26.685 2.799 11.213
1 171 115.498 2.799 4.542 2 367 284.007 2.837 10.544
3 484 373.707 2.821 6.507 4 853 544.649 2.719 8.098
4 853 544.649 2.719 8.098 5 1240 722.803 2.698 7.539
5 1240 722.803 2.698 7.539 N/A
Total Trip Fuel Cost: $ 103.398 Total Trip Fuel Cost: $ 103.655
Table 2 displays the following results for the scenario: a listing of on which days
to stop, at which gas stations to stop, the price of gas at each station, and how much
gas should be purchased at each station. The first column (Optimization) provides the
solution when the objective function is to minimize to cost of fuel over the trip and α
is set to zero such that there is no penalty for the number of stops. The second col-
umn (Optimization with Penalty) provides the results for the optimization model that
includes a penalty in the objective function each time the driver has to stop for gas;
this enforces user preferences on how many times a day and per trip they are willing
to stop (see equation 5). Here we set α = 1, but the value of α could vary depending
on the number of gas stations considered in the route. If we compare the results for the
optimization models with different objective functions, we see the difference caused by
the penalty in the objective function: it eliminates an additional stop on the first day for
a slight increase in overall cost of around $.25.
Table 3 shows the results for both heuristic methods when applied to this scenario.
The first column gives the solution when the driver stops for gas right before their fuel
gage registers the minimum gas allowed (2 gallons in this scenario). The second column
gives the results of the greedy heuristic, which looks for the lowest priced gas between
when the fuel gage registers half a tank and 2 gallons.
70
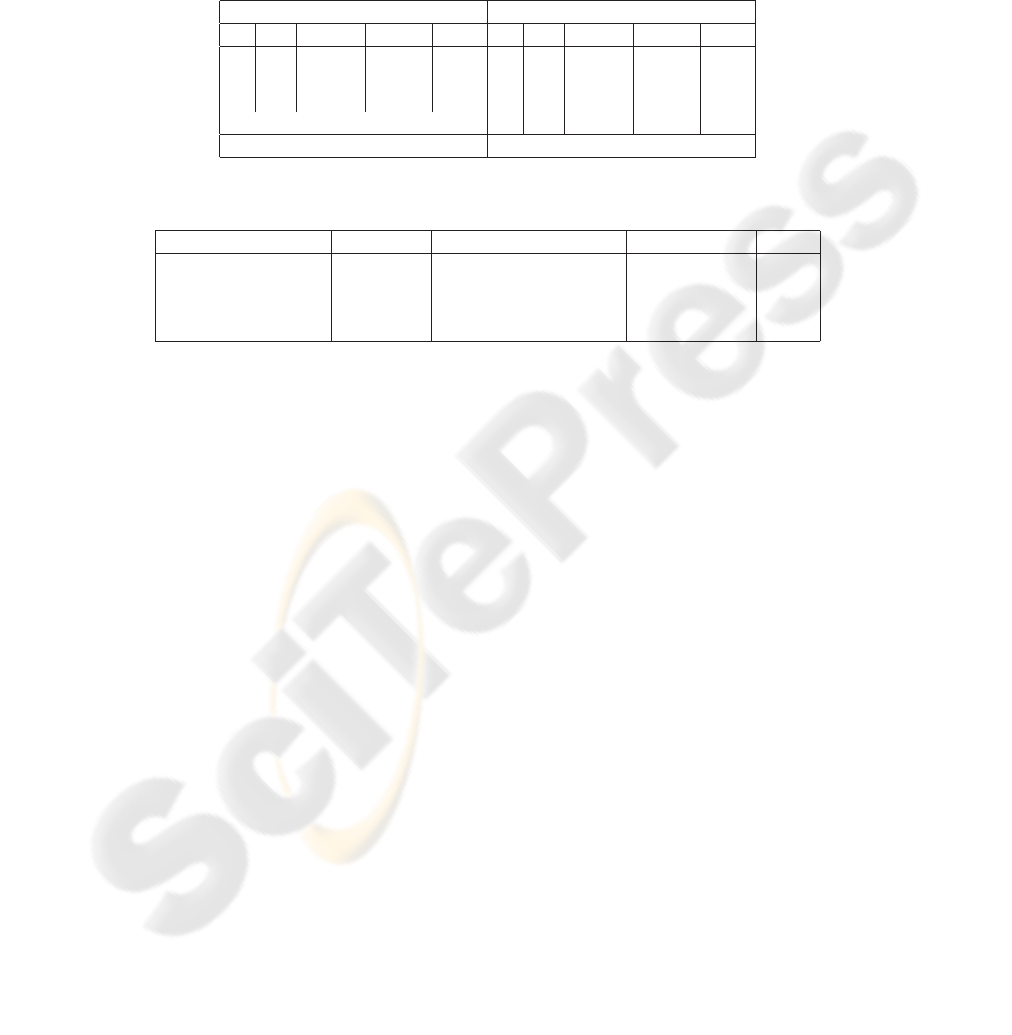
Table 4 compares the results of the four approaches. The heuristic, which has the
driver stop at the closest gas station when they reach 2 gallons of gas in their tank, results
in the fewest stops and eliminates only partially filling up the gas tank when stoping.
However, this technique does result in the highest total fuel cost which is 6.44% higher
than the original optimization technique.
Table 3. Scenario Results for Heuristic Methods.
Stop At 2 Gallons Greedy Heuristic
Day ID Distance Price ($) Buy Day ID Distance Price ($) Buy
1 101 65.892 2.999 12.995 1 41 26.685 2.799 11.213
2 432 350.930 2.946 12.956 2 381 290.172 2.837 11.977
4 1061 636.879 2.877 11.442 4 924 563.492 2.719 12.424
N/A 5 1446 829.094 2.698 1.78
Total Trip Fuel Cost: $ 110.06 Total Trip Fuel Cost: $ 103.945
Table 4. Technique Comparison.
Optimization Optimization with Penalty Stop at 2 Gallons Greedy
# Stops 5 4 3 4
Stops Fill < 10 Gallons 4 2 0 1
Total Cost ($) 103.398 103.655 110.06 103.945
% Over Lowest Cost N/A 0.25% 6.44% 0.53%
7 Conclusions
With fuel prices on the rise in the United States, drivers are increasingly concerned with
their refueling strategy. This paper presented a model to assist drivers with decisions
regarding where and when to refuel along with how much fuel to purchase. The model
takes into account various factors, such as user preferences (e.g. how often the driver
is willing to stop for gas) and vehicle specific information (e.g. the current fuel level).
Gas stations along a specified route can be identified and gas prices corresponding to
future days of the route can be determined using the forecasting method discussed in
Section 4. Once this information has been aggregated, it is used by the Mixed Integer
Programming model presented in Section 5.1 to provide the driver with an optimal
refueling strategy. As shown in section 5.2 heuristical approaches can also be used to
determine a refueling strategy.
Future versions of this model can be extended to include additional driver prefer-
ences or economic factors. For example, by considering flex-fuel vehicles, the refueling
decision becomes even more complex as the analysis would include tradeoffs between
the price per gallon of fuel, average miles per gallon associated with a particular route
and vehicle, and possibly the CO2 effects for multiple fuel types. In addition, we could
move towards a more advanced forecasting model and provide a refueling strategy that
would take into consideration multiple routes for a single origin destination pair.
The proposed model offers substantial benefits over existing approaches. First, it
provides an optimal refueling strategy using forecasted fuel prices over multiple time
71

periods and locations as opposed to a local strategy based on a small geographical
region and the current fuel prices in that area. In addition, the vehicle internal network
can be used to monitor the current fuel level and consumption to offer proactive advice
instead of waiting for the driver to request help from the system. Finally, over time the
system can learn a driver’s regular routes and associated fuel consumption to provide
more accurate recommendations in the proposed refueling strategy.
Acknowledgements
We would like to thank Jenny Lin at Corporate Economics of Ford Motor Company for
providing the 5 series of wholesale prices.
References
1. BMW. BMW website. http://www.bmwusa.com/Standard/Content/Owner/
BMWAssist/Default.aspx, 2008.
2. Borenstein, Cameron & Gilbert. Do gasoline prices respond asymmetrically to crude oil
price changes? TheQuarterlyJournalofEconomics,Vol.112,1997, 1999.
3. Dash. Dash website. http://www.dash.net/, 2008.
4. Eckert, & West. Retail gasoline price cycles across spatially dispersed gasoline stations.
JournalofLawandEconomics,April,2004, 2004.
5. Energy Information Administration. Price changes in the gasoline market. http://
tonto.eia.doe.gov/FTPROOT/petroleum/0626.pdf, 1997.
6. Farecast. Our Technology and Data website, 2008. http://www.farecast.com/
about/ourTechnology.do.
7. Ford Motor Company. Popular Ford SYNC System Expanded; New SIRIUS ”Travel Link”
Takes Navigation to New Level website, 2008. http://media.ford.com/article_
display.cfm\?article_id=27489.
8. J. Froehlich and J. Krumm. Route predictions from trip observations. Society of Automotive
Engineers (SAE) 2008 World Congress, April 2008.
9. Garmin. https://buy.garmin.com/shop/shop.do?pID=13479, 2008.
10. GasBuddy. GasBuddy website. http://www.gasbuddy.com/, 2008.
11. GasPriceWatch. GasPriceWatch website. http://www.gaspricewatch.com/, 2008.
12. William Greene. Econometric Analysis. Prentice Hall, 2007.
13. E. Horvitz, P. Koch, and M. Subramani. Mobile Opportunistic Planning: Methods and Mod-
els, pages 228–237. Lecture Notes in Computer Science. Springer Berlin, 2007.
14. Integrated Decision Support. Planning and Execution Solutions for Truckload Carriers: Ex-
pert Fuel website, 2008. http://www.idscnet.com/software/fuel.htm.
15. E. Kamar, E. Horvitz, and C. Meek. Mobile opportunistic commerce: Mechanisms, archi-
tecture, and application. In Proceedings of AAMAS 2008, Estoril, Portugal, May 2008.
16. A. Kapoor and E. Horvitz. Experience sampling for building predictive user models: A
comparative study. In Proceedings of CHI 2008, Florence, Italy, April 2008.
17. Ludovic Privat. TomTom to offer real-time fuel price to GO 920. GPS Business News,
January 10 2008.
18. OnStar. OnStar website. http://www.onstar.com/, 2008.
19. OPIS. OPIS website. http://www.opisnet.com/, 2008.
20. The Gas Game. The Gas Game website. http://www.thegasgame.com/, 2008.
21. L. Wolsey. Integer Programming. John Wiley & Sons, Inc., 1998.
72
