
An Authentication Protocol for Wireless Ad Hoc
Networks with Embedded Certificates
Robert E. Hiromoto
1
and J. Hope Forsmann
2
1
Department of Computer Science, University of Idaho, Moscow, Idaho 83844-1010, U.S.A.
2
Idaho National Laboratory, 2525 N. Fremont, Idaho Falls, Idaho 83415, U.S.A.
Abstract. Wireless ad hoc networks may be configured as a fixed topology of
sensors or allowed to migrate as mobile nodes. The flexibility of these networks,
therefore, provides opportunities for their deployment in real-time and in adverse
situations as encountered in civil and military applications. These advantages are,
unfortunately, curtailed by the unconstrained nature of these networks in pro-
viding a trusted level of connectivity. The establishment of secret keys and the
authentication of trusted ad hoc group nodes are essential elements for a secure
network. In this paper, we develop an authentication protocol for wireless ad hoc
networks that is derived from a canonical splitting of time- and frequency-space
(channel) over which information propagates under the constraint of a collision-
avoidance protocol.
1 Introduction
The rapid deployment of wireless ad hoc networks even under the most severe condi-
tions, has elevated their prominence in all aspects of homeland security and military
communications. However, these infrastructure-less networks are prone to require ex-
plicit network cooperation, route maintenance in the event of link failure, and informa-
tion losses resulting from data packet collisions. These routing protocols for dynamic
networks have been discussed in [11] and [19]. Furthermore, without data encryption
and trusted node authentication, these networks are vulnerable to malicious attacks that
may be categorized by the following techniques: eavesdropping; man-in-the-middle;
replay; impersonation; session hijacking; reflection; and interleaving attacks.
Intelligent information processing provides network security approaches that has
prompted researchers to propose numerous security protocols for the establishment of
secret keys; and in particular, the authentication of wireless ad hoc network nodes. A
taxonomy and classification of services that rely on authentication are studied by [17,
10]. The use of local time-stamp authentication protocols [14], a hop-by-hop authenti-
cation [26], recommendation and reference protocol that is inspired by human behav-
ior [24], location-limited channels with pre-authentication [20, 1], an end-to-end data
authentication scheme that relies on mutual trust between nodes [23], a threshold se-
cret sharing using an identity-based cryptosystem to provide end-to-end authentication
[6], under loosely time synchronized nodes with one-way chain as a cryptographic key
where each such value is associated with a time interval [25].
E. Hiromoto R. and Hope Forsmann J. (2008).
An Authentication Protocol for Wireless Ad Hoc Networks with Embedded Certificates.
In Proceedings of the 4th International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 89-99
DOI: 10.5220/0001509500890099
Copyright
c
SciTePress

In [3], a self-organized public-key management scheme is proposed that maintains
no centralized services, yet, allows each node to generate private-public key pairs; to
issue public key certificates for its neighboring nodes; and to perform authentication
via a chain of public-key certificates regardless of the network partition. Several re-
finements to this proposed scheme are presented in [2] where each certificate is issued
with a limited validity time period that contains its issuing and expiration time. After
expiration of the valid time period, new certificate are issued to its neighboring nodes.
In addition, nodes in alliance with their neighboring nodes form trust groups that com-
municate using the group’s private and public key. The authenticity between nodes is
performed by validating their cached public-key certificates chain. The public keys and
certificates are modeled as a directed graph for which transitive properties can identify
nodes belonging to a trust group.
A major difficulty with the solution specifications for certificate-based authentica-
tion, as described above, is the amorphous structure of wireless ad hoc networks in both
static and dynamic systems. The unconstrained nature of malicious attacks in such net-
works are, therefore, difficult if not impossible to protect against. Geometrically, the use
of public/private-key certificates is a one-dimensional parameterization of the problem
domain. Whether in the form of a certificate-chain or a cluster-key shared with multiple
neighboring nodes, the various approaches are limited by their reliance on artificial so-
lutions that do not embrace the dynamical properties or behavior of these systems. With
this in mind, we argue for a “canonical” reformulation of the authentication problem in
wireless ad hoc networks and derive an alternative solution technique that is described
in a two-dimensional setting.
If security is deemed critical then as in all practical engineering considerations,
tradeoffs must be identified and enforced. To this end, we propose a different approach
to authentication in wireless ad hoc networks that imposes a collision-avoidance policy
on data transmission that has the property of untangling the authentication process such
that certificates are no longer exchanged explicitly.
In the remainder of the paper, we outline the proposed approach, and provide pos-
sible means of implementations.
2 An Authentication Protocol with Embedded Certificates (APEC)
The proposed authentication protocol introduces a sequence of unique, non-overlapping
communication time-slots that are assigned to each authenticated node of the network.
Time-slots are used as an implicit certificate to ensure trust. In addition, we impose on
top of each time-slot a pseudo-randomly corollated frequency channel F
i
over which a
data packet must be sent in time-slot T
i
. This dependence between time-slots and fre-
quency channels introduces a two-dimensional description of network communication
and thus allows for a clear decomposition of the problem domain.
The protocol is described in terms of a cluster with a single cluster head or admin-
istrator node as follows:
1. Assume that an initial authentication phase has verified the trust of nodes that have
joined the cluster.
81

2. The cluster head sends a public key to all nodes in the cluster.
3. The public key is used by every node to select the appropriate addem, multipliers,
etc to construct a common pseudo-random number generator (PRNG) using a hash-
table. Two such PRNGs are constructed RandT() and RandF, that produces the
sequences for T
i
and F
i
; respectively.
4. From the public key, a random seed is produce and used to seed RandT(). Each T
i
that is generated is in turn used as a seed to generate a corresponding F
i
from the
pseudo-random number generator RandF().
5. After each complete communication time period, the order of the sequence of time-
slots are permuted.
At the end of these steps, a sequence of T
m
time-slots with their randomly corre-
lated frequency channel, F
m
, are created, and forms m-coordinate, 2-tuples (T
i
, F
i
).
In addition, the details of the PRNG construction are known to each entrusted node in
the network; and therefore, allows a deterministic recreation of all present and future
m-coordinate pairs. This becomes important when a node cannot send data packets to
the cluster head in one hop but instead requires a multi-hop link to reach its destination.
3 A Space-Time Coordinate Basis with Collision-Avoidance
Communication can be parameterized as a space-time, 2-tuple coordinate basis. Time
(time-slot), T
i
, is taken as the moment (over the time-slot duration) that a message
is sent or received. Space is the physical channel over which the message is sent or
received. For a wireless network this channel is associated with a particular radio fre-
quency, F
i
, over which a message is sent out or received. We characterize this 2-tuple
by (T
i
, F
i
).
In order to avoid ambiguities, it is important that a collision-avoidance protocol be
adopted for a wireless network so that no two data packets arrive at a given destination
during the same time-slot. This property is reflected in the following definition:
Definition: Two valid communication coordinates (T
i
, F
j
) and (T
r
, F
s
) within a wire-
less ad hoc network must necessarily satisfy the condition that T
i
6= T
r
; however, it
is not sufficient since some time-slots may be forbidden. (collision-avoidance assump-
tion).
The collision-avoidance assumption restricts a clustered network of wireless nodes
to communicate only over predetermined, non-overlapping send or receive time-slots.
As a consequence, certain types of external attacks can be detected if two or more
distinct data packets arrive during the same time-slot.
The collision-avoidance assumption is examined by Forsmann et al., [8]. The per-
spective of their study is the QoS of unmanned aerial vehicles for autonomous formation
flight. For the sake of this paper, we consider only the cluster formation with a single
cluster head node, and assume that all communication is directed between a cluster
head and each individual node within the cluster. It is, however, possible that the mobil-
ity of each vehicle (node) may require the use of intermediate nodes to form a multi-hop
message-forwarding link if the sending node drifts out of radio range with the cluster
82

head. Multi-hop network routing links are addressed using a modified version of the
AODV route-discovery protocol as described by Forsmann et al.
Under the assumptions of a collision-avoidance protocol and the two-dimensional
representation of communication events within a wireless mobile ad hoc network, we
introduce a cryptographic confusion algorithm that replaces the traditional certificate-
based authentication procedures that have been attempted for these infrastructure-less
networks. The following desired set of properties provide the foundation for our ap-
proach:
Property 1: A unique time-slot and frequency channel pair is assigned to only one node
within the network.
Property 2: It is desirable to conceal the selection of the radio frequency channel F
i
in
each round of a node’s communication time-slot sequence.
Property 3: For each communication period a new sequence order for a given node’s
time-slots T
i
are assigned.
Property 4: The length of a time-slot duration depends upon the time-skewing experi-
ence by each node’s clock. It will be assume that each node is equipped with a GPS
device for time synchronization.
The process for concealing the selection of T
i
and F
i
is performed using a pair of
orthogonal PRNGs as outline in Frederickson et al., [9]. Their work examined the issue
of reproducibility of Monte Carlo random walk algorithms for parallel execution. The
use of a single PRNG in a parallel processing environment has the effect of reordering
the sequence of pseudo-random numbers that are generated. Although this additional
randomness may seem advantageous, the final result cannot be compared for correct-
ness with the results of the sequential execution that uses the same PRNG. Without this
verification, it is not clear whether or not the parallel program has been implemented
correctly.
Analogously, a wireless ad hoc network represents a collection of parallel process-
ing nodes that can be assured a unique {T
i
, F
i
} pair for each entrusted node without
incurring inter-node co-channel interference. To ensure this property, each node must
be given a different random number sequence in a deterministic fashion. Figure 1 illus-
trates the orthogonal structure for a pair of PRNG that result in a reproducible random
number scheme.
Below, we summarize some typical PRNGs in use and techniques used in creating
parallel pseudo-random number generators (PPRNG).
4 Pseudo-Random Number Generation
4.1 Types of Generators
The following list are commonly used pseudo-random number generators:
– Additive and subtractive Lagged Fibonacci (LF)
– Generalized Shift Register (GSR)
83

Fig. 1. RanT and RanF .
– Multiplicative Linear Congruential (MLC) and
– Combination Generators (CG)
A uniform (double precision) floating-point random number sequence x
i
in the interval
[0, 1) or (0, 1) are produced by the following recursions:
MLC (a, m = 2
l
):
X
i
= aX
i−1
mod m; x
i
= X
i
/m, (i = 1, 2, ...)
GSR (r, s, ⊕
l
):
X
i
= X
i−r
⊕
l
X
i−s
; x
i
= X
i
/2
l
, (i = r, r + 1, ...) (1)
LF (r, s, ±m = 2
l
):
X
i
= X
i−r
± X
i−s
mod 2
l
; x
i
= X
i
/2
l
, (i = r, r + 1, ...)
CG:
Z
i
= X
i
Y
i
; (i = r, r + 1, ...)
where is either the exclusive-or-operator or addition modulo some integer m, and X
and Y are sequences from two independent generators. It is best if the cycle length of
the two generators is relatively prime, for this implies that the cycle length of Z will be
the product of that of the basic generators. One can show that the statistical properties
of Z are no worse than those of X or Y [15]. Good combined generators have been
developed by L’Ecuyer [13], based on the addition of Linear Congruential sequences.
4.2 Parallel Pseudo-Random Number Generation
Historically, the introduction of PPRNG was an attempt to address various efficiency
issues inherent in the parallel execution of scientific applications such as lattice gauge
and Ising model calculations. Within this context, the quality of PPRNGs have been
studied by a number of researchers [4], [5], [16], [18],[21]. More recently, their use in
games and graphics have drawn interest [22], [12].
As a brief overview, we list below several approaches that have been studied and
applied in the design of PPRNGs. The descriptions are only meant to provide a high
level, structural description of several different possible parallel techniques.
84

– Leapfrog – The pseudo-random sequence is partitioned in turn among nodes so
that node i gets the sequence r
i
, r
i+m
, . . ., where m is the total number of nodes or
time-slots.
– Sequence splitting – The sequence is partitioned by splitting it into non-overlapping
contiguous sections. In particular, if it is known that the cycle length of a pseudo-
random sequence is l
c
then node i + 1 gets the sequence r
[il
c
/m]+1
, r
[il
c
/m]+2
, . . .
r
(i+1)l
c
/m
.
– Independent sequences – For some generators, the initial seeds can be chosen in
such a way as to produce long period independent subsequences on each processor.
– Cycle parameterization – For PRNGs’ that have more than one distinct cycle, it is
possible to select a seed that begins in one cycle and a different seed that begins
in a different cycle resulting in two sequences that do not overlap. The Lagged
Fibonacci Generator is an example of a generator with this property. By associating
each seed with a cycle number i, parameter i determines the cycle from which the
sequence is drawn.
4.3 Reproducibility and Cycle Lengths
In order to ensure reproducibility, each node must be given a different random number
sequence in a deterministic fashion. This can be accomplished by creating a random
seed unique to each node (e.g., the time-slot) that in turn is used to seed a different
(orthogonal) random number generator that produces a second “independent ” pseudo-
random (frequency channel) sequence. This deterministic approach is reproducible and
requires no inter-node communication, whose costs are typically high. More impor-
tantly, the absence of inter-node communication is extremely desirable from a security
standpoint.
A pseudo-random number generator defines at most 2
b
different configurations
(states) where b is the number of bits that represent the number of possible states. The
sequence, after generating 2
b
different configurations, must repeat .
It is desirable, therefore, to use PPRNGs with the longest cycle length to guarantee
the minimal biasing of the results. This, however, does not eliminate the advantages of
a small cycle length as long as the coordinates that are produced are not exactly the
same. Hence even if the random number sequence repeats, if the {T
i
, F
i
} pair remain
unique, the bias remains low.
As a consequence, it is assumed that the correlation between pairs of pseudo-random
number generators has little effect on network authentication unless the bias results in
(T
i
, F
j
) cycles.
4.4 Security
Pseudo-random number generation is a process that either provides security or is vul-
nerable to attacks that can compromise the security of a system. The PRNG process
is provocatively attractive to attackers because it is typically a single isolated, hard-
ware/software component whose deterministic output is disguised as random. If an
attacker can substitute pseudo-random bits generated in a way that can be predicted,
security is totally compromised.
85
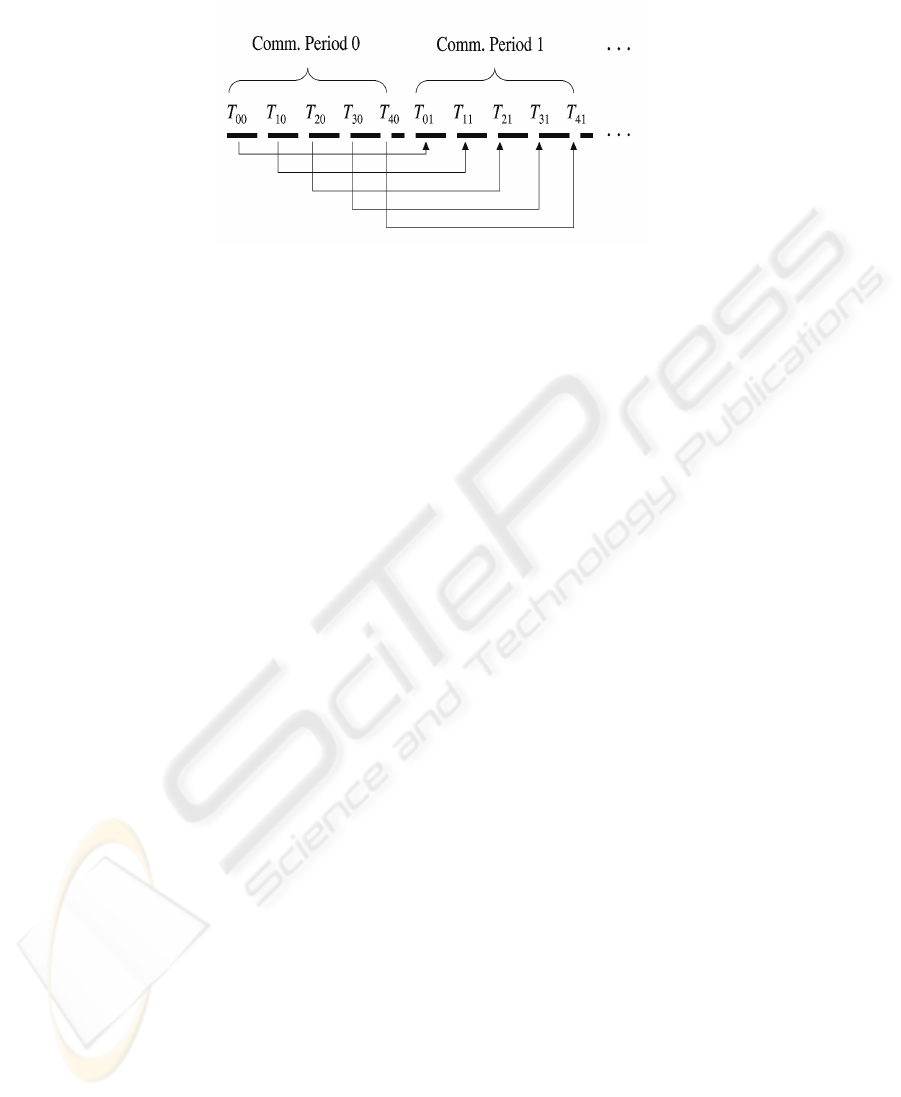
Fig. 2. Direct Mapping Constant Increment δt
i
= τ .
5 Time-Slot Selection
The sequence of time-slots for one complete communication period
{T
0
, T
1
, . . . , T
n
, . . . , T
m−1
, }
A communication period, τ, is defined as the sum over all m time-slots (m ≥ n) in
the closed interval [T
0
, T
m−1
],
τ =
m−1
X
i=0
T
i
.
The requirement (m ≥ n) for an n node wireless network is imposed for three reasons.
First, m may be viewed as a cryptographic parameter that introduces a level of confu-
sion, as is shown later. Second, the choice of m introduces idle time-slots over which
no data packets should be sent or received. Third, m provides a slight window (delay)
between the end of one time-slot and the beginning of the next.
After each communication period, a new sequence of unique non-overlapping time-
slots are assigned to each node. This assignment is defined by the following equation:
T
j,i+1
= T
j,i
+ δt
i
, (2)
for i, j = 0, 1, . . . , m. In this notation index j is the node number and i is the iteration
or communication period number.
There are several ways of selecting δt
i
. One simple approach is to maintain the
order of time-slots for each node from one iteration to the next. Figure 2 illustrates the
case for δt
i
= τ.
A second and possibly more secure approach is to apply a permutation on the order
of the previous time-slot sequence. The permutation of the sequence is shown in Fig. 3.
For a permutation π, we associate a permutation matrix P
π
and a distance matrix
D
π
whose values represent the number of column swaps from their original position to
their final position in the permutation. For example, if π = {0, 3, 2, 1}, then
86

Fig. 3. Permutation Mapping Variable Increment δt
i
.
P
π
=
1 0 0 0
0 0 0 1
0 0 1 0
0 1 0 0
,
and
D
π
=
0 0 0 0
0 0 0 −2
0 0 −1 0
0 +2 0 0
.
The distance matrix can then be used to define a time-slot increment vector δt
i
given by
δt
i
= τ θ
T
+ δtD
π
· θ, (3)
where
θ =
1
1
.
.
.
1
of length m, and
δt = τ /m.
The components of Eqn. 3 are then applied to Eqn. 2.
87

5.1 Multi-Hop Authentication
The requirement for pseudo-random reproducibility is most important in the instant
that a network topology has migrated beyond a single-hop radio range to a multi-hop
environment. In such a situation, a routing protocol is employed to initiate route dis-
covery. As part of the data transfer process, the destination node may have need of
the source nodes identity and the chosen route path. To obtain this information any
entrusted node intercepting the packets can recompute the node’s time-slot seed using
the original public-key and compute the appropriate frequency channel for the current
communication period. With this information, the source node and route path can be
identified. The implications of this scenario is that only trusted nodes can determine the
communication route, destination and source nodes in a calculable time frame.
5.2 Security Complexity
APEC is a cryptographic system protocol based on a source of random bits, whose
output is used in creating unique time-slot and frequency channel pairs. APEC employs
two “orthogonal” pseudo-random number generators that cooperate in parallel to assign
node-specific send/receive, time-slots that are in turn used to seed a pseudo-random as-
signment of time-slot, correlated frequency channels. In this construction, the sequence
of frequency channels can be systematically applied in turn to the same time-slot but on
different periods of the communication cycle.
The order of time-slots assigned to each node can remain in the same order or be
reordered to increase cryptographic confusion. In this paper, a reordering of the time-
slot sequence is presented using a simple permutation π.
The security complexity is stated by the following theorem.
Theorem: The brute force complexity for guessing the correct sequence of coordinate
basis pair for a b-bit random sequence and a permutation of the sequence order for m
time-slots is O(2
2b
× m!).
Proof: A pseudo random number generator is a finite state machine with at most 2
b
different states where b is the number of bits that represent the state. The brute force
complexity of guessing the time-slots is O(2
b
). However, since the frequency channels
are coupled to the seed of a unique time-slot the complexity of the coupled random
number states requires a total of O(2
2b
). If we also apply a permutation to the previous
time-slots sequence for every communication period the brute force complexity for m
time-slots is O(m!). The final complexity is the product of the time-slot, frequency
channel and the permutation operations. 2
6 Conclusions
Geometrically, the use of public/private keys as certificates for authentication in wire-
less ad hoc networks is a one-dimensional solution in a two- or higher-dimensional
problem domain. The novel abstraction taken here is to design an authentication pro-
tocol that embodies the dynamic processes and captures the essential behavior of the
88

system in a “self-certifiable” manner. In this context, we achieve a canonical formula-
tion of the authentication problem in wireless ad hoc networks and as such derive an
alternative solution technique devoid of explicit certificate passing.
The contributions of this paper is the design of a new authentication protocol that
relies on a collision-avoidance protocol to guarantee the detection of unauthorized at-
tempts to compromise a wireless ad hoc network of trusted nodes. The protocol creates
a random, yet deterministic sequence of coupled time-slots and associated frequency
channels that are unique to each node in the network. For each communication period,
the order of the sequence of time-slots may remain unaltered or the order can be re-
arranged deterministically without coordination via inter-node communication. If an
analogy can be made between frequency channels to colors in the visual range, the
communication in an APEC system would appear to be a coordinated light show.
References
1. D. Balfanz, D. K. Smetters, P. Stewart and H. Chi. Wong, “Talking to Strangers: Authen-
tication in Ad-Hoc Wireless Networks,” Symposium on Network and Distributed Systems
Security (NDSS ’02).
2. Chih-Peng Chang, Jen-Chiun Lin, Feipei Lai, “Trust-group-based authentication services for
mobile ad-hoc networks,” 1st International Symposium on Wireless Pervasive Computing,
16-18 Jan. 2006,
3. Srdjan Capkun, Levente Buttyan, Jean-Pierre Hubaux, “Self-Organized Public-Key Manage-
ment for Mobile Ad-hoc Networks,” in ACM International Workshop on Wireless Security,
WiSe 2002.
4. Chiu, T. W. “Shift-register sequence random number generators on the hypercube concurrent
computers,” in G. C. Fox, editor, The Third Conference on Hypercube Concurrent Computers
and Applications, Volume 2, pages 1421-1429 (1988).
5. Paul D. Coddington and Sung-Hoon Ko, “Techniques for empirical testing of parallel random
number generators,” Proceedings of the 12th international conference on Supercomputing,
pp. 282 - 288 (1998).
6. H. Deng, A. Mukherjee, D. P. Agrawal, “Threshold and Identity-Based Key Management and
Authentication for Wireless Ad Hoc Networks,” International Conference on Information
Technology: Coding and Computing (ITCC’04) (2004).
7. W. Diffie, P.C. van Oorschot, and M.J. Wiener, “Authentication and authenticated key ex-
changes,” Designs, Codes and Cryptography 2 (1992).
8. J. Hope Forsmann, Robert E. Hiromoto, and John Svoboda, “A Time-Slotted On-Demand
Routing Protocol for Mobile Ad Hoc Unmanned Vehicle Systems,” SPIE 2007, Orlando
Florida, April 9-12 2007.
9. P. Frederickson, R. Hiromoto, T. Jordan, B. Smith, and T. Warnock, “Pseudo-Random Trees
in Monte Carlo,” Parallel Computing, Vol. 1, No. 2, pp. 175-180, (December 1984).
10. S. Hahm, Y. Jung, S. Yi, Y. Song, I. Chong, and K. Lim, “Self-organized Authentication
Architecture in Mobile Ad-hoc Networks,” International Conference on Information Net-
working (ICOIN) (2005).
11. D.B. Johnson and D.A. Maltz, “Dynamic Source Routing in Ad Hoc Wireless Networks,”
Mobile Computing, vol. 353, Kluwer Academic Publishers (1996).
12. Sylvain Lefebvre and Hugues Hoppe, “Perfect Spatial Hashing,” ACM Trans. Graph. 25, 3,
579588 (2006).
89

13. P. L’Ecuyer, “Efficient and portable combined random number generators,” Comm. of the
ACM, 31:742774, 1988.
14. H. Lou, P. Zerfos, J. Kong, S. Lu, and L. Zhang, “Self-Securing Ad Hoc Wireless Networks,”
Seventh IEEE Symposium on Computers and Communications (ISCC’02).
15. G. Marsaglia, “A current view of random number generators,” In Computing Science and
Statistics: Proceedings of the XVIth Symposium on the Interface, pages 3-10, 1985.
16. M. Mascagni S. A. Cuccaro and D. V. Pryor, ”Techniques for testing the quality of parallel
seudorandom number generators”, In Proceedings of the Seventh SIAM Conference on Par-
allel Processing for Scientific Computing, pp. 279-284, Philadelphia, Pennsylvania, 1995.
SIAM.
17. D. Park, C. Boyed, E. Dawson ”Classification of Authentication Protocols: A Practical Ap-
praoch”, Proceedings of the Third International Workshop on Information Security.
18. O. E. Percus and M. H. Kalos, ”Random number generators for MIMD parallel processors,”
J. of Par. Distr. Comput., 6:477-497, 1989.
19. C. Perkins, ”Ad Hoc On Demand Distance Vector (AODV) Routing”, Internet Draft, draft-
ietfmanet-aodv-00.txt, November 1997.
20. F. Stajano and R. Anderson, “The Resurrecting Duckling: Security Issues in Ad-Hoc Wire-
less Networks”, M. Roe B. Christianson, B. Crispo, editor, Security Protocols, 7th Interna-
tional Workshop Proceedings, LectureNotes in Computer Science. Springer Verlag, 1999.
21. A. Srinivasan, D. M. Ceperley and M. Mascagni, ”Random Number Generators for Parallel
Applications,” in Monte Carlo Methods in Chemical Physics, D. Ferguson, J. I. Siepmann,
and D. G. Truhlar, editors, Advances in Chemical Physics series, Volume 105, John Wiley
and Sons, New York (1998).
22. Stanley Tzeng and Li-Yi Wei, “Parallel White Noise Generation on a GPU via Cryptographic
Hash,” Proceedings of the 2008 symposium on Interactive 3D graphics and games, (2008).
23. L. Venkatraman and D. Agrawal, “A Novel Authentication Scheme for Ad Hoc Networks,”
IEEE Wireless Communications and Networking Conference (WCNC 2000), vol. 3, pp.
1268-1273.
24. A. Weimerskirch and G. Thonet, “A Distributed Light-Weight Authentication Model for Ad-
hoc Networks,” Proc. of 4th International Conference on Information Security and Cryptol-
ogy (ICISC 2001).
25. S. Zhu, S. Setia and S. Jajodia, “LEAP: Efficient Security Mechanisms for Large-Scale Dis-
tributed Sensor Networks,” 10th ACM Conference on Computer and Communications Secu-
rity (CCS ’03) (2003).
26. S. Zhu, S. Xu, S. Setia and S. Jajodia, “LHAP: A lightweight hop-by-hop authentication
protocol for ad-hoc networks,” Proc. of ICDCS 2003 International Workshop on Mobile and
Wireless Network (MWN 2003), May 2003.
90
