A Predictive Controller for Object Tracking of a Mobile

Robot

Xiaowei Zhou, Plamen Angelov and Chengwei Wang

Intelligent Systems Research Laboratory

Lancaster University, Lancaster, LA1 4WA, U. K.

Abstract. In this paper a predictive controller for real-time target tracking in

mobile robotics is proposed based on adaptive/evolving Takagi-Sugeno fuzzy

systems, eTS. The predictive controller consists of two modules; i) a

conventional fuzzy controller for robot motion control, and ii) a modelling tool

for estimation of the target movements. The prediction of target movements

enables the controller to be aware and to respond to the target movement in

advance. Successful prediction will minimise the response delay of the

conventional controller and improve the control quality. The model learning

using eTS is fully automatic and performed ‘on fly’, ‘from scratch’. Data are

processed in ‘one-pass’ manner, therefore it requires very limited computational

resource and is suitable for on-board implementation on the mobile robots.

Predictions are made in real-time. The same technique also has the potential to

be used in the process control. Two reference controllers, a controller based on

the Mamdani-Type fuzzy rule-base, and a controller based on the simple linear

model, are also implemented in order to verify the proposed predictive

controller. Experiments are carried out with a real mobile robot Pioneer 3DX.

The performance of the three controllers is analyzed and compared.

1 Introduction

The main objective of the object tracking is controlling the robot to maintain a

constant distance and heading to the mobile object being tracked [1]. A simple first

priciple controller can be used for this purpose based on the linearisation of the

problem [2]. Alternatively, in a pursuit of more accurate tracking, a fuzzy controller

can be applied. A fine tuned fuzzy controller [3] can achieve higher accruacy

comparing to the simple linear controllers. However, one problem that the

conventional controllers are facing is that the controller generates the manipulated

value (control command) according to the observation of system status at the current

and the past time instants while the purpose of the control is to minimise the observed

error in the forthcoming (future) time instant. Taking into account the dynamic nature

of the target system, this delay, in response may lead to larger errors. For this reason,

a predictive controller which is able to predict the behavour of the target system is

recommended in such cases [4]. Instead of a response to the directly observed

measurements, the so called model-based predictive controller (MBPC) makes the

control decision based on the predicted values. Therefore, a predictive model is an

indispensable part of any MBPC scheme [4]. In [5] a Takagi-Sugeno (TS) fuzzy

Zhou X., Angelov P. and Wang C. (2008).

A Predictive Controller for Object Tracking of a Mobile Robot.

In Proceedings of the 2nd International Workshop on Intelligent Vehicle Control Systems, pages 73-82

 SciTePress

model has been used as a model predictor. This model, however, was pre-trained off-

line and was with a fixed strtucture. The eTS concept introduced recently [6]-[8]

allows the TS fuzzy model to be designed on-line, ‘on fly’ during the process of

control and operation. This is especially suiatble and convenient for applications such

as robotics where the autonomous mobile robots may be required to operate in a

completely unknown, dynamic, or harsh environment [9].

The main problems in controllers design [10] are; i) their stability; ii) their tuning.

The former problem is not treated in this paper. The latter one is usually approached

in off-line mode and also from the point of view of adpative control theory [2] which

is well developed for the linear case [11]. In a dynamcially changing environment

eTS fuzzy systems have their advantage of flexibility and open structure. Moreover,

they have been used in conjunction with so called indirect learning proposed by

Psaltis in 1998 [12] described in [6] and [12]. While Psaltis and Anderson et al. [14]

used off-line pre-trained and with fixed structure neural networks for their indirect

learning scheme in [6] and [13] evolving FLC is used that learns ‘on fly’, ‘from

scratch’ based on the operational data alone and no pre-training.

In this tracking problem, the desired velocity of the two side wheels of the robot is

controled. The distance, d and the angle to the moving target, θ are measured at each

sampling time, Figure 1. The objective of the control is to maintain a predefined

distance to the target so that the target is closely followed without a collison

(reference distance, d

ref

). A heading angle of 0

to the target is also required.

Fig. 1. Target tracking by a mobile robot.

The structure design of the conventional controller used as a basis benchmark for this

test of target tracking by the mobile robot is illustrated in Figure 2. The current state

described by the distance to the target, velocity of both wheels of the mobile robot

(left and right) measured by the sensors mounted on the mobile robot Pioneer 3DX is

fed back to the controller. The controller has a fixed structure and parameters that are

determined based on common knowledge of the problem.

Fig. 2. Controller schematic.

1.1 First Principles-based Controller

The first principles-based controller used for this task is based on the explicit linear

description of the problem. In order to follow the moving target, the acceleration of

the robot is assumed to be proportional to the distance to the target, d. Due to the

inertia of the real systems it takes a short period of time after a velocity command is

received by the motor the desired velocity to be reached. Therefore, the velocities of

both wheels (left and right) are selected as control values. The turning of the robot is

achieved by control of the velocity difference between the left and right wheels.

When the velocity of the left wheel is higher than the velocity of right wheel, the

robot makes a right turn and vice versa. Based on these principles, the wheel velocity

control model is described by the following equations:

rfright

lfleft

VVV

(1)

It consists of two components; V

, the component for maintaining d

ref

and the pair of

velocities, V

, and V

which determine the heading of the mobile robot. The two

components are defined by equations (2)-(3) below, also illustrated in Figure 3.

Figure 3a) and 3b) illustrate the linear components which describes the control

response in proportion to the distance and heading difference to the target

respectively. When the distance to the target is Far the velocity component, V

is set

to High, which leads to a larger acceleration of the robot. While the distance is below

ref

(set in our experiments to 400mm), the velocity component, V

is set to Negative.

Fig. 3a. Distance component. Fig. 3b. Angle component.

)(

1 reff

ddkV

−

(2)

⎪

⎩

⎪

⎨

⎧

θθθ

θθ

;

⎪

⎩

⎪

⎨

⎧

>−

θθθ

θθ

(3)

Where

are threshold values; k

and k

are coefficients.

1.2 Fuzzy Controller

In an attempt to achieve a more flexible and accurate tracking, a Mamdani type fuzzy

logic controller (FLC) has also been implemented [10]. It consists of five fuzzy rules:

The fuzzy rule base of the Mamdani type FLC:

Rule 1:

IF (d is Crash) AND (

is Negative)

THEN (V

is Quick Back) AND (V

is Quick Back)

Rule 2:

IF (d is Close) AND (

is Straight)

THEN (V

is Slow Back) AND (V

is Slow Back)

Rule 3:

IF (d is proper) AND (

is Small Positive)

THEN (V

is Hold) and (V

is Hold)

Rule 4:

IF (d is Not Far) AND (

is Small Negative)

THEN (V

is Slow Forward) AND (V

is Hold)

Rule 5:

IF (d is Far) AND (

is Positive)

THEN (V

is Slow Forward) AND (V

is Quick Forward)

Each rule describes a typical situation during the tracking task. Real-time readings are

obtained to form an input vector. The closeness from the measured input vector to the

prototypes (focal points) of each fuzzy rule is calculated based on triangular

membership functions illustrated in Figure 4. The result is aggregated to form the

degree of firing for each rule and normalised and aggregated further to form the

overall output of the FLC [10]. The antecedent part of the fuzzy rules is defined by

linguistically interpretable terms that describe the distance (Figure 4) and angle; the

consequent fuzzy sets are defined in respect to the velocity.

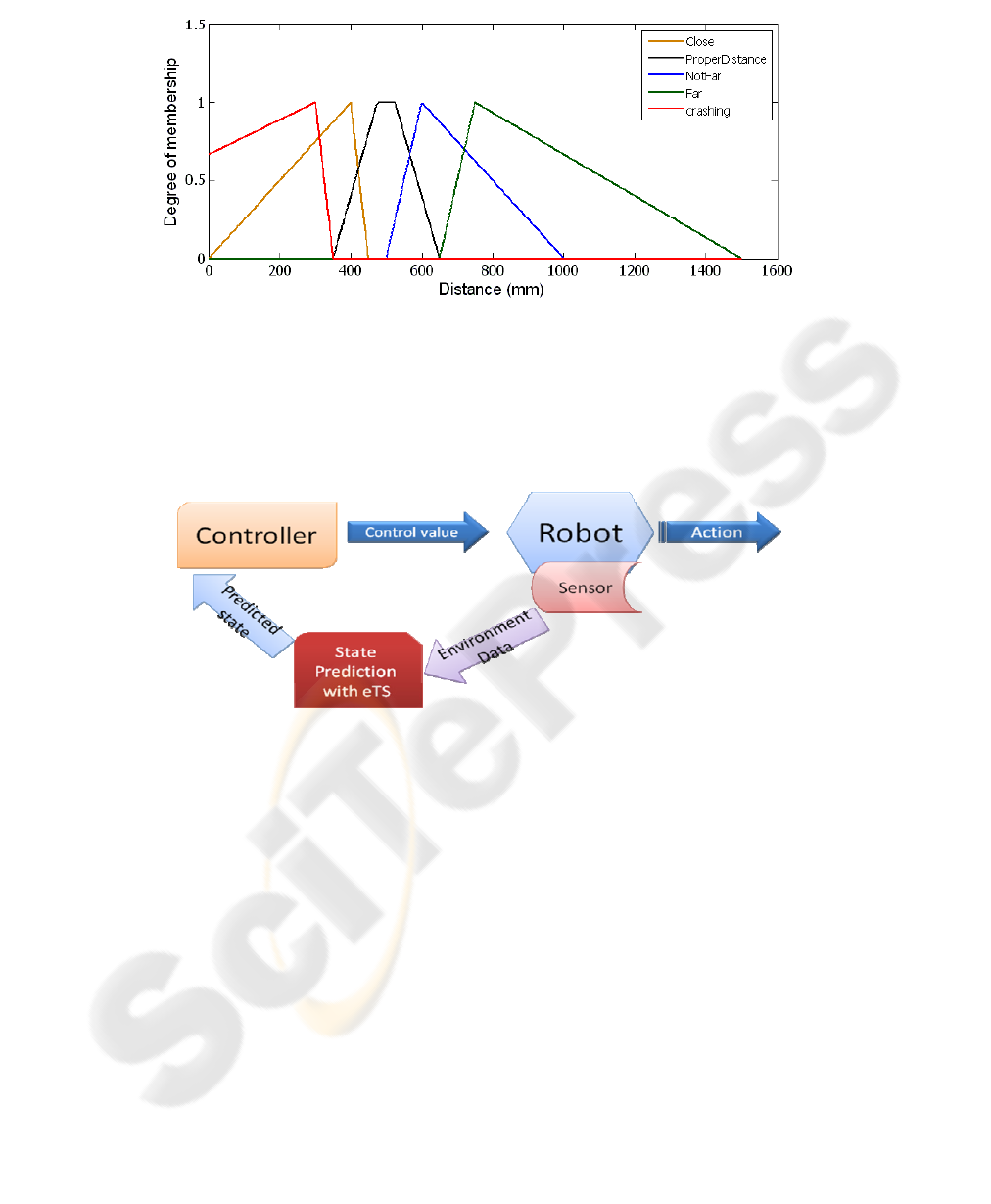
Fig. 4. Fuzzy Sets for Distance.

The fuzzy controller is tuned by an off-line optimization testing a group of randomly

chosen fuzzy sets settings.

1.3 Predictive Controller

Fig. 5. System Structure of the predictive controller.

In the design of the MBPC, a prediction module is added to the FLC described above.

The prediction module is based on eTS [6-8] and aims to predict the distance and

angle to the moving target one time instant ahead based on the information of current

distance, angle, and velocity of both wheels. These predicted values are then fed to

the FLC instead of the readings of the distance and angle at current step. The MBPC

then determines the control values in the same way, but based on the predicted values.

This leads to minimisation of the tracking error caused by the delay in the response in

velocity due the time required by acceleration. The evolving Takagi-Sugeno predictor

is described in more details elsewhere [6-8] and is sketched in the following diagram.

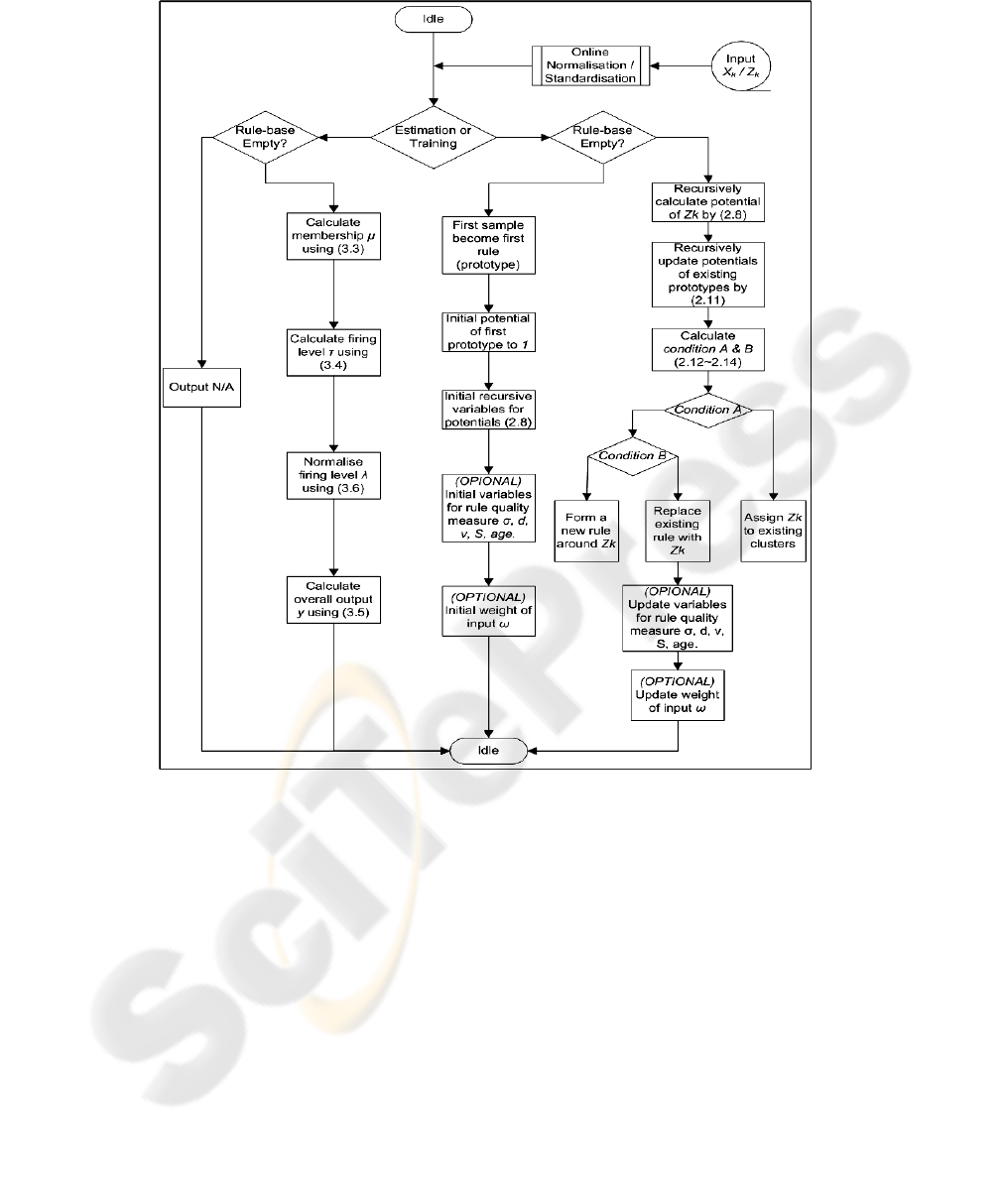
Fig. 6. Flow chart of the evolving Takagi-Sugeno (eTS) Predictor Algorithm.

2 Experimental Study

2.1 The Robots

The experiment is carried out with a Pioneer3 DX mobile robot [15] equipped with an

onboard PC and a laser ranging device. The laser scans a fan area of 180 degrees and

returns the distance and headings to the closest obstacle in this fan area. The

detectable range of the laser is [150mm, 10,000mm]. In the experiment, another

mobile robot played the role of the moving object to be tracked, following

automatically a predefined routine (see Figures 7 and 8). There is no external links

such as GPS and the wireless data connection is used only to download data. Thus,

the task is performed fully unsupervised by the mobile robot.



Fig. 7. The robots and the experiment.

Fig. 8. Route of the target object.

2.2 Experimental Settings

Four variables were measured in real-time:

1 distance to the object;

2 angle to the object;

3 the real velocity of the left wheel

4 the real velocity of the right wheel of the robot being controlled.

The sampling frequency is about 10Hz (100ms per sample). The control values are

generated at each sampling interval.

Table 1. An example of the data collected in real-time with the control outputs.

Time d, mm

θ,

Real Left,

mm/s

Real Right,

mm/s

Ctrl Left,

mm/s

Ctrl Right,

mm/s

0 205.295 -5.04 -110 -118 -763.923 -799.234

200 201.297 -5.53 -42 -10 -773.8 -812.551

400 207.336 -16.9 -43 -88 -716.216 -835.137

600 216.334 0.068 -93 -133 -750.034 -749.551

801 207.263 10.47 -107 -167 -739.24 -812.532

1001 246.715 3.49 -282 -274 -676.127 -651.682

The experiment was carried out outside Infolab21, Lancaster University, UK. For

each of the tested controllers a group of ten tests were carried out along the same test

route as shown in Figure 8. During the test the target object performed a series of

behaviours including acceleration, deceleration, turning, reversing, etc. The mobile

robot that is performing the tracking task has the controllers uploaded on its on-board

PC written in C language. The tracking task is performed fully automatically. Only

the laser ranging device was used to measure both the angle and the distance. The

velocity is measured by the tachometer (odometer) of the robot [15].An example of

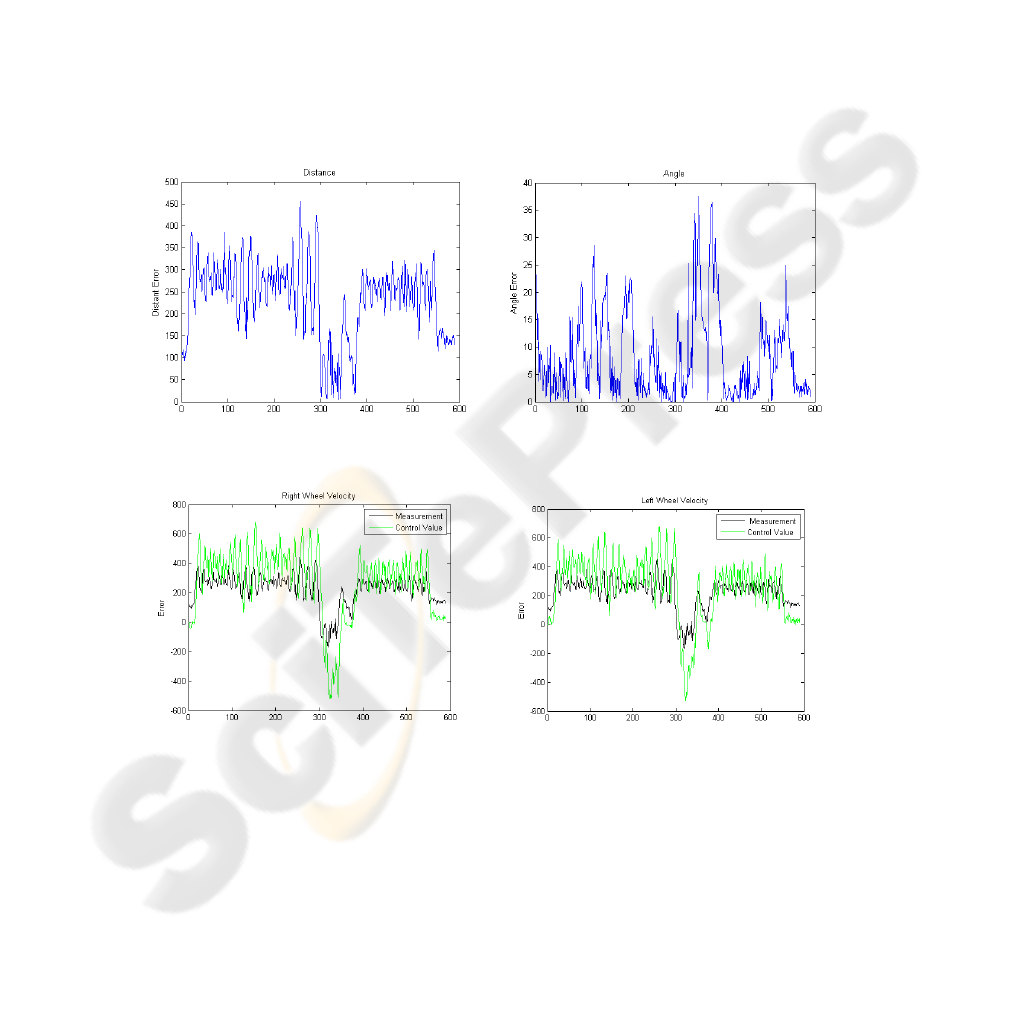
the measured distance and angle difference to the target is illustrated in figure 9a) and

9b). Several pre-tests were also carried out to find the suitable parameters for the

FLC. The distance and the angle to the target were measured in real-time. The

discrepancy between the real observation and the target values of distance and angle

has been used to calculate the errors. The mean absolute error (MAE), the standard

deviation (STD) and the root mean square (RMSE) are used as the criteria for the

comparison of the three controllers.

Fig. 9a) Distance measured in real-time. Fig. 9b) Angle measured in real-time.

Fig. 10. Control values versus real observations for velocity of the wheels.

3 Results Analysis and Conclusions

The results are tabulated in table 2. They show that the prediction module in the

predictive controller has assisted the fuzzy controller to achieve better control

precision in terms of the distance and to some extent in terms of the tracking angle

minimising the delay in control response. Note that as shown in table 1 and Figure 10,

there is some overshot (the control values generated by the fuzzy controller and the

predictive controller are larger than the desired velocity of the wheels). This is

because it has already taken into account the response delay in time required for the

acceleration/deceleration.

Table 2. Result Comparison.

d, mm

RMSE MAE STD RMSE MAE STD

First Principles Controller

83.3 129.2 110.1 4.8 9.35 8.14

FLC

70.2 120.3 113.7 4.9 7.43 7.34

MBPC 65.2 112.5

119.9

4.8

7.53 7.09

In table 2, on can see that the angle tracking by the FLC is worse than that of the First

principles-based controller. To improve on this aspect, more rules describing the

response to different observation in angles can be added to the fuzzy controller to

achieve higher control accuracy. Off-line techniques such as ANFIS [16] can be used

in order to get the optimal parameters of the fuzzy controller for the task.

In the future, real time image classification [9] and tracking techniques [17] can be

integrated with the proposed predictive controller. In this way, image-based

information can be used by the prediction module of the MBPC which is expected to

further improve the precision.

References

1. Liu P. X., M. Q.-H. Meng (2004) Online Data-Driven Fuzzy Clustering with Applications

to Real-Time Robotic Tracking, IEEE Transactions on Fuzzy Systems, vol.12, No 4, 2004,

pp.516-523.

2. Astrom K. and B. Wittenmark (1984) Computer Controlled Systems: Theory and Design,

Prentice Hall: NJ USA, 1984.

3. Carse B., T.C. Fogarty, A. Munro (1996) Evolving Fuzzy Rule-based Controllers using

GA, Fuzzy Sets and Systems, v.80, pp.273-294.

4. Clarke D, Advances in Model-based Predictive Control, Oxford University Press, Oxford,

UK, 1994.

5. Babuska R (1998) Fuzzy Modelling for Control, Kluwer Publishers, Dordrecht, The

Netherlands.

6. Angelov, P., Evolving Rule-based Models: A Tool for Design of Flexible Adaptive

Systems. Berlin, Germany: Springer Verlag, 2002.

7. Angelov, P., Filev, D., “An Approach to On-line Identification of Takagi-Sugeno Fuzzy

Models”, IEEE Transactions on System, Man, and Cybernetics, part B - Cybernetics,

vol.34, No1, 2004, pp.484-498. ISSN 1094-6977.

8. Angelov P and X Zhou (2006) Evolving Fuzzy Systems from Data Streams in Real-Time,

In Proc. 2006 International Symposium on Evolving Fuzzy Systems, Ambelside, Lake

District, UK, IEEE Press, pp.29-35, ISBN 0-7803-9719-3.

9. Zhou. X., P. Angelov, An Approach to Autonomous Self-localization of a Mobile Robot in

Completely Unknown Environment using Evolving Fuzzy Rule-based Classifier, First 2007

IEEE International Conference on Computational Intelligence Applications for Defense and

Security, April 1-5, 2007, Honolulu, Hawaii, USA, pp.131-138.

10. Yager R R and D P Filev (1993) Learning of Fuzzy Rules by Mountain Clustering, Proc. of

SPIE Conf. on Application of Fuzzy Logic Technology, Boston, MA, USA, pp.246-254.

11. Kailath, T, Linear systems, Prentice Hall, US, 1980.

12. Psaltis D, A Sideris, A A Yamamura (1998) A Multilayered Neural Network Controller,

Control Systems Magazine, vol. 8, pp. 17-21.

13. Angelov P P (2004) A Fuzzy Controller with Evolving Structure, Information Sciences,

ISSN 0020-0255, vol.161, pp.21-35.

14. Andersen H.C., F.C. Teng, A.C. Tsoi (1994) Single Net Indirect Learning Architecture,

IEEE Transactions on Neural Networks, v.5 (6), pp.1003-1005.

15. Pioneer-3DX (2004) User Guide, ActiveMedia Robotics, Amherst, NH, USA.

16. Jang, J.-S., RANFIS: adaptive-network-based fuzzy inference system, IEEE Transactions

on System, Man, and Cybernetics, vol.23, No3, 1993, pp.665-685.

17. Angelov P., R. Ramezani, X. Zhou, Autonomous Novelty Detection and Object Tracking in

Video Streams using Evolving Clustering and Takagi-Sugeno type Neuro-Fuzzy System,

2008 IEEE Intern. Conf. on Fuzzy Syst. within the IEEE World Congress on

Computational Intelligence, Hong Kong, June 1-6, 2008, to appear.