A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY

CONSTRUCTION

Yin-Fu Huang and Yu-Yu Huang

Graduate School of Computer Science and Information Engineering

National Yunlin University of Science and Technology, 123 University Road, Section 3, Touliu, Yunlin, Taiwan 640

Keywords: Ontology construction, ontology learning, Is-A and Parts-of relationships, word correlation, hierarchical

clustering.

Abstract: This paper proposed a general framework that could automatically construct domain ontology on a

collection of documents with the help of The Free Dictionary, WordNet, and Wikipedia Categories. Both

explicit and implicit features of index terms in documents are used to evaluate word correlations and then to

construct Is-A relationships in the framework. Thus, the built ontology would consist of 1) concepts, 2) Is-A

and Parts-of relationships among concepts, and 3) word relationships. Besides, the built ontology could be

further refined by learning from incremental documents periodically. To help users browse the built

ontology, an ontology browsing system was implemented and provided different search modes and

functionality to facilitate searching a variety of relationships.

1 INTRODUCTION

With high developments of digital media and

networks, everyone can create and deliver electronic

documents easily, rapidly, and unrestrictedly. More

and more publications are created on digital media,

but readers are troubled with such huge amounts of

data. For this reason, developing ontology that can

bring a conceptual schema of millions of documents

to readers is necessary.

A general description about ontology is that

ontology is a specification of an abstract, simplified

view of the world that we wish to represent for some

purpose, and it is increasingly important in many

information systems and semantic web (Yan-Hwang,

2005). This description gives us a brief

understanding about ontology, and some more

definitions about ontology can be found in (Riichiro,

2003 and Thanh, 2006), which let us realize what

these papers want to construct. Based on these

descriptions or definitions, we conclude that three

basic elements exist in ontology; i.e., concepts,

relations among them, and axioms to formalize the

definitions and relations. When it comes to relations,

the primary ones are Is-A and Parts-of relationships.

The framework of building ontology proposed in the

paper would focus on this issue. However,

constructing ontology is a time consuming and

tremendous work, even if it is built manually. For

example, the most famous ontology in biology, Gene

Ontology (http://www.geneontology.org/) was

defined by professionals one by one. In summary, it

is quite not easy to construct ontology automatically.

The paper developed a framework automatically

constructing domain ontology with the help of The

Free Dictionary (http://

www.thefreedictionary.com/), WordNet (http://

wordnet.princeton.edu/), and Wikipedia Categories

(http://en.wikipedia.org/wiki/Special:Categories).

Since there is still no famous ontology on the

computer science domain and many open resources

on the domain facilitate building the ontology, the

paper aims to construct the computer science

ontology as a case study. The built ontology would

consist of 1) concepts, 2) Is-A and Parts-of

relationships among concepts, and 3) word

relationships.

The remainder of the paper is organized as

follows. Section 2 describes related preliminary

work on ontology generation. In Section 3, the

framework to construct ontology from a collection

of documents is proposed. Then, the case study of

computer science ontology construction and the

ontology browsing system are discussed and

presented in Section 4. Finally, we make conclusions

in Section 5.

Huang Y. and Huang Y. (2008).

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 16-25

DOI: 10.5220/0001516800160025

 SciTePress

2 RELATED PRELIMINARY

WORK

Although there have been some researches exploring

on ontology, most of them focused on using specific

ontology to assist their work, rather than on building

ontology. On the other hand, other researches (Trent,

2002, Rowena, 2005, Dave 2001, Sin-Jae, 2001,

Yan-Hwang, 2005, Alexander, 2000, Riichiro, 2003,

Thanh Tho, 2006, Prieto-Diaz, 2003, Yuri A., 2003

and Ju-in Youn, 2004) addressed building ontology.

They could be classified into two categories in

building ontology (strictly speaking, some of them

are just to propose a schema of object entities). The

first one is to classify documents into their domain

based on key terms which are organized by several

words in documents (Florian, 2002, Dave, 2001,

Weipeng, 2001, Yin-Fu, 2007, Thanh Tho, 2006 and

Ju-in, 2004). The other one is to classify keywords

to construct a taxonomy structure based on

belonging documents, thesauri, or pre-built ontology

(Trent, 2002, Rowena, 2005, Sin-Jae, 2001, Yan-

Hwang, 2005, Alexander, 2000, Prieto-Diaz, 2003,

Vaclav, 2005 and Yuri A., 2003).

Youn et al. (Ju-in Youn, 2004) first constructed

the ontology by fuzzy function and relations, and

then classifies documents based on this ontology. In

fact, the ontology constructed here is just a word

relation tree similar to that proposed (Yin-Fu Huang,

2007). Besides, two papers (Florian, 2002 and Yin-

Fu, 2007) also provide schemas of documents, and

the classification on documents has the same

characteristics, since each cluster of documents (or

each tree node in word relation tree) implies the

same term feature. However, their methodologies

are different where one is how to select term features

to do clustering, and another is how to stretch the

current level to the next one.

Since building ontology is so tremendous, it

should be maintained incrementally, rather than

building from scratch. Some learning techniques to

refine the built ontology were proposed (P. Buitelaar,

2005, Asunción, 2003 and Alexander, 2001), and

even general relationship learning (not focusing on

Is-A or Parts-of relationships) has been discussed

(M. Kavalec, 2004, David, 2006 and A. Schutz,

2005). In our framework, new incremental

documents could be imported periodically, and then

the learning process uses them to refine word

relationships in the same way.

2.1 Key Terms for Generating

Ontology

Term-Document-Matrix (TDM) records the

frequency that each key term appears in documents,

and it is also called weighted word histogram

(Weipeng, 2001). Key terms and documents are two

dimensions in TDM. If we take the dimension of

documents as our classified target, key terms can be

viewed as feature (Florian, 2002, Dave, 2001,

Weipeng, 2001 and Teuvo, 2000), and vice versa.

Usually, it is necessary to build ontology to present

the overall context structure on web pages. Tijerino

et al. developed an information-gathering engine,

TANGO, to exploit tables and filled-in forms to

generate domain-specific ontology (Yuri A., 2003).

In our framework, TDM is treated as the implicit

feature to evaluate word correlations.

FOLDOC (http://foldoc.org/) is an online

computing dictionary, in which each keyword and

its relatives are tagged to show their relationships.

Apted and Kay followed its original relationships

between words, and transferred the whole keywords

in the dictionary into a clear relation graph of

keywords (Trent Apted, 2002). Although it has

stored about 14,000 computing terms till now, many

computing terminologies are not yet stored inside.

2.2 Features of Key Terms

Besides the documents as the input source,

additional dictionaries are required to build ontology

(Sin-Jae, 2001 and Alexander, 2000). The features

of key terms retrieved from documents and

dictionaries help to build ontology, which could be

generalized as three kinds; i.e., document vectors,

sememes, and the meaning coming from

dictionaries.

Sememes are defined as the smallest basic

semantic unit in HowNet (K. W. Gan, 2002). Some

papers (Yi, 2002 and Yan-Hwang, 2005) took

sememes as feature roles to do further processing.

However, many computing terms are special

terminologies, the meanings of which could be

different from their original words. Thus, viewing

sememes in computing terms as features could not

be feasible here. Finally, since FOLDOC does not

have enough computing terms for our work, the

instruction inside it is somewhat inadequate to

provide further features. Therefore, we choose The

Free Dictionary instead as the explicit feature

provider.

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION

2.3 Measuring the Correlations

between Key Terms

Many kinds of methods can be used to measure the

correlations between key terms. One of them is to

evaluate the ratio of co-occurrences in sememes

between key terms (Yi, 2002 and Yan-Hwang,

2005). Some are to apply similarity functions to

compute the similarities between key terms based on

document features, such as Cosine coefficient,

Jaccard coefficient, and Dice coefficient (Jim Z. C.,

2002). Among these similarity functions, Cosine

coefficient is the most frequently used (Weipeng,

2001 and Latifur, 2002). The others are to apply

fuzzy analyses to assign the similarities (Rowena,

2005, Weipeng, 2001, Thanh Tho, 2006 and Ju-in,

2004). In our framework, besides using Cosine

coefficient, several rules are also defined to measure

the correlations of key terms in Section 3.2.2.

2.4 Constructing the Relationships in

Ontology

There are several methods to construct the

relationships between concepts. The first method is

to apply hierarchical clustering such as fuzzy

hierarchical clustering (Rowena, 2005). Hierarchical

clustering could be further classified into top-down

and bottom-up approaches. Top-down approaches

consist of HFTC (Florian, 2002), hierarchical SOM

(Dave, 2001), and GH-SOM (Michael, 2000),

whereas bottom-up ones include HAC (Latifur,

2002). The second method is to use the existing

relations between concepts to identify the relation

(Trent, 2002, Sin-Jae, 2001 and Vaclav, 2005). The

last one is to build association networks of concepts

based on fuzzy similarity (Thanh Tho, 2006 and Ju-

in, 2004). National language processing (or

morphological analysis) also joins force (Yan-

Hwang, 2005). The other methods could be mixed

ones such as combining SOM clustering with

merging process (Weipeng, 2001) or with statistic

methods (Richard C., 1996 and W. B., 1992), and so

on.

Even if a few papers as mentioned built

ontology, none of them explored to construct the

relationships between concepts, such as Is-A or

Parts-of relationships. Is-A refers to a relationship

is a

⎯

⎯→ where A is a kind of B, and inherits

all the properties of B. On the other hand, Parts-of

refers to a relationship

parts of

CD⎯⎯⎯⎯→ where C is

a part of D and has only partial properties of D.

In the paper, Wikipedia Categories and WordNet

is considered as knowledge bases to assist in

retrieving Is-A and Parts-of relationships from the

dataset. Wikipedia Categories is a specific

classification of keywords, and each keyword in

Wikipedia at least belongs to one category. Thus, the

structure of Wikipedia Categories is a directed

graph, and can be used to retrieve Is-A relationships

from the dataset.

WordNet is a large lexical database of English

where nouns, verbs, adjectives, and adverbs are

grouped into sets of cognitive synonyms (synsets),

each expressing a distinct concept. There are two

types of Parts-of relationships in WordNet; i.e.,

Meronym and Holonym. Meronym denotes a

constituent part of (or a member of) something. For

example, X is Meronym of Y if X(s) are parts of

Y(s). But Holonym is opposite to Meronym.

Holonymy defines the relationship between a term

denoting the whole and a term denoting a part of the

whole. For example, X is Holonym of Y if Y(s) are

parts of X(s). The type of a Parts-of relationship

could be part, member, substance, so that there are

totally six kinds of Parts-of relationships; i.e., part-

meronym, member-meronym, substance-meronym,

part-holonym, member-holonym, and substance-

holonym. Since key terms investigated here are

nouns, we would retrieve these six kinds of Parts-of

relationships of nouns in WordNet

3 SYSTEM FRAMEWORK

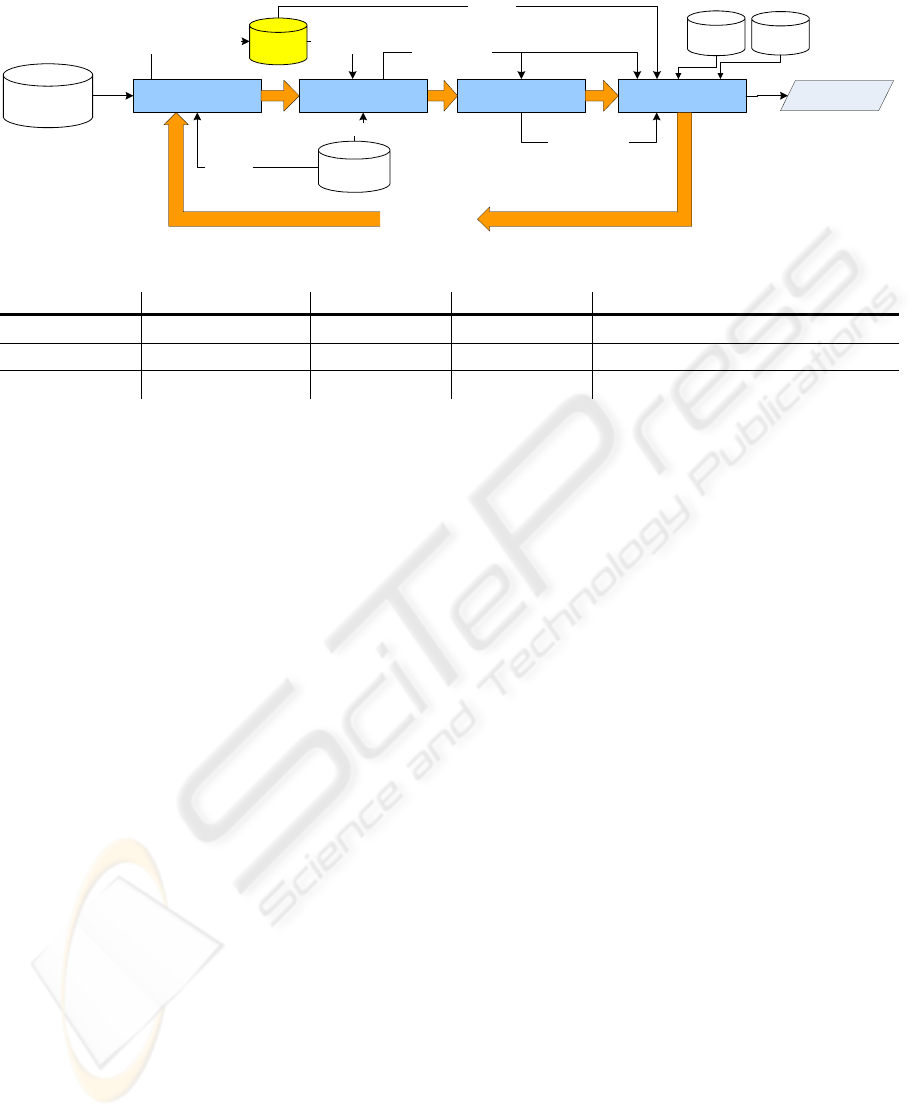
As shown in Fig. 1, the system framework of

ontology construction consists of four components

where the built ontology could be refined

periodically. The explanations are as follows.

(1) Relationship Summary Extractor: The

relationship summary extractor extracts the

computing terms from the documents archived

in INSPEC (http://www.iee.org/publish/inspec/)

to create Term-Document-Matrix, and also the

related words such as synonyms, antonyms, etc

from free dictionaries to create Relative-Matrix.

Both matrices are stored in the local database

for the next refinement.

(2) Correlation Matrix Generator: The correlation

matrix generator computes the correlations

between the key terms.

(3) Concept Hierarchy Constructor: The concept

hierarchy constructor builds a concept hierarchy

for further finding sophisticated relationships.

(4) Sophisticated Relationship Extractor: The

WEBIST 2008 - International Conference on Web Information Systems and Technologies

Relationship Summary

Extractor

Incremental T-D Matrix,

Incremental Relative Matrix

Concept Hierarchy

Constructor

Synonyms,

Antonym,

Acronyms

Relatives

Ontology

Sophisticated

Relationship Extractor

Correlation Matrix

Generator

Unique Acronyms

INSPEC

Bibliographic Info.

The Free

Dictionary

WordNetWikipedia

Concept Hierarchy

Key Terms

Learning Phase

Correlation Matrix

Local Matrix

Database

T-D Matrix,

Relative Matrix

Figure 1: System framework.

Figure 2: Relative-Matrix where KT and T represent terms, and KT

is the same as T

sophisticated relationship extractor retrieves the

Is-A and Parts-of relationships from individual

input and specific external knowledge bases

(e.g., Wikipedia and WordNet).

The built ontology in the learning phase could be

refined periodically where the whole processes

would be executed again, given incremental

documents as input.

3.1 Relationship Summary Extractor

The functionality of Relationship Summary

Extractor is to extract vector spaces used to evaluate

the correlations between key terms in the ontology.

We have two kinds of data sources; i.e., document

vector extracted from INSPEC bibliographic

information, and relative vector retrieved from sub-

dictionaries in The Free Dictionary.

For document vector, index terms (or keywords)

in every document could be distinguished into two

categories, subject headings and key phrase

identifiers that are also called controlled and

uncontrolled indexing respectively in IEL

(http://ieeexplore.ieee.org/Xplore/guesthome.jsp.).

Only the index terms filtered through the filtering

process would be the key terms in the ontology.

According to the definition of indexing in INSPEC

(http://www.lib.nus.edu.sg/lion/slb/d/SD/inspec/insc

ont.html), since uncontrolled indexing contains free-

language words or phrases assigned by INSPEC

indexers, and has a wider range of terms, it has less

weighting than controlled one. Thus, the Term-

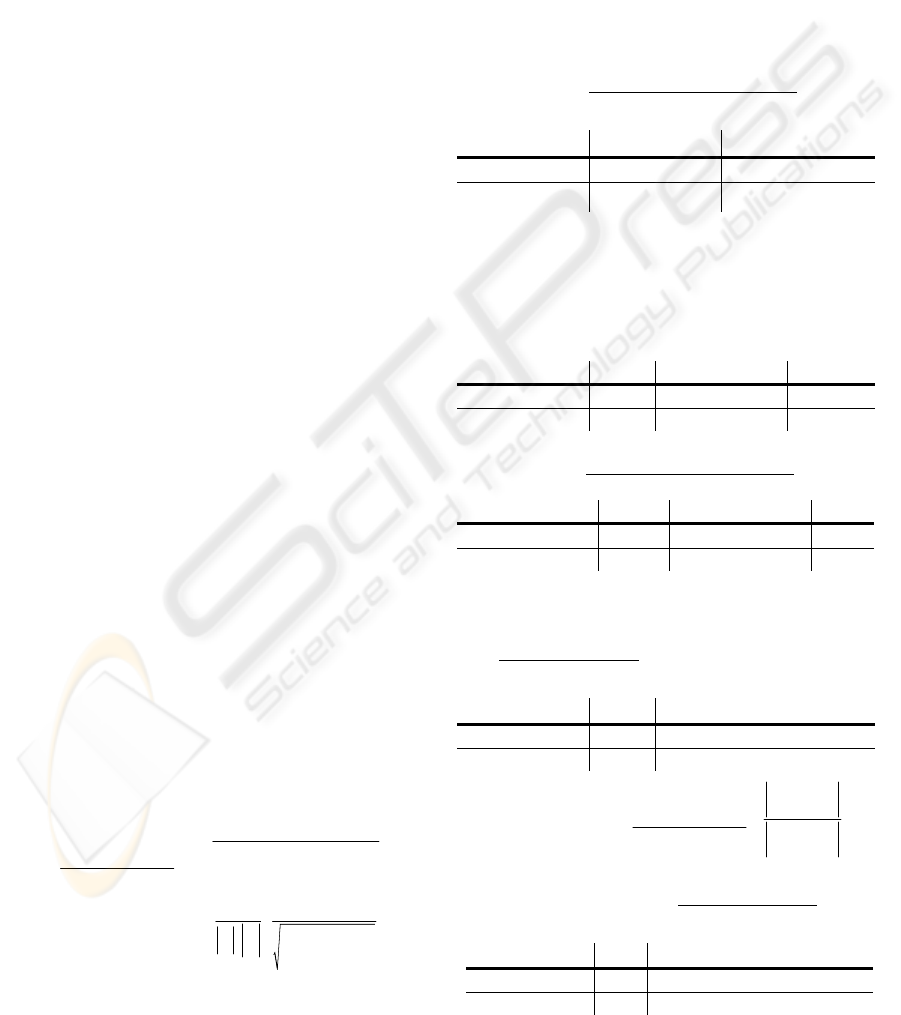
Document-Matrix is defined as follows.

where w

is the weight of key term i in document

j, m is the no. of key terms, n is the no. of

documents, KT is a key term, S is a set of key terms

with subject heading, and K is the one of key terms

with key phrase identifier.

For relative vector, the terms could be synonyms

or relatives. There are ten sub-dictionaries in The

Free Dictionary, but only four of them, called

Dictionary/thesaurus, Acronyms, Computing

Dictionary, and Wikipedia Encyclopedia, are used as

references. Since we aim to construct computer

science ontology, Computing Dictionary is chosen

as the target. The synonyms and antonyms of terms

are collected from Dictionary/thesaurus, the

acronyms from Acronyms, and the relatives from

Dictionary/thesaurus, Computing Dictionary, and

Wikipedia Encyclopedia. The Relative-Matrix

organized by relative vectors is shown in Fig. 2.

In summary, Relationship Summary Extractor

extracts each individual vector for each key term,

and finally produces Term-Document-Matrix and

Relative-Matrix.

3.2 Correlation Matrix Generator

The next step is to combine two matrices produced

in the last step into one matrix. However, since there

are some duplicate terms in these two matrices, such

as “database” and “databases”, a merging process

should be done before combining the matrices.

Key Terms Synonyms Antonyms Acronyms Relatives

, T

… … … T

, T

… … … T

, T

… … … …

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION

11 1 1

3, & in

2, in

1, in

0, otherwise

ij i i j

ij i j

iij

ij i j

mmjmn

www

wKTSKTKDoc

wKTSDoc

wKTKDoc

www

⎛⎞

=∈ ∈

⎧

⎜⎟

⎪

=∈

⎜⎟

⎪

⎨

⎜⎟

=∈

⎪

⎜⎟

⎪

⎜⎟

⎩

⎝⎠



 







3.2.1 Merging Duplicated Terms

Even if two index terms are individual, they could

be the same thing or have the same meaning, so

duplicates should be merged. For example,

single/plural nouns and unique acronyms are the

cases of duplicates. If there is more than one

duplicate, this step would merge document and

relative vectors of all duplicates. For single/plural

nouns, WordNet or a stemming process could be

used to solve this issue. For unique acronyms, we

can find them only for exact one key term in the

dataset. For example, acronym “SOM” can represent

either “Self Organizing Map” or “Semantic Object

Model”, so “SOM” is not a unique acronym.

However, acronym “RISC” plays the abbreviation

role only for “Reduced Instruction Set Computing”

in the dataset, so “RISC” is a unique acronym.

3.2.2 Combining Term Document Matrix

and Relative Matrix

After merging Term-Document-Matrix and Relative-

Matrix respectively, these two matrices would be

combined into Correlation-Matrix showing the

correlations between each term pairs. The

correlations between each term pairs could be

computed as

(, ) (, )

(1 ) ( , )

where 0.5 1.

yRMxy

TDM x y

Correlation KT KT Correlation KT KT

Correlation KT KT

=×

+− ×

≤≤

(1)

Here, Relative-Matrix is considered as more

important than Term-Document-Matrix, since the

former implies more explicit correlations between

terms than the latter.

As for Correlation

and Correlation

TDM

Equation (1), they can be computed as the following

equations

(, )

(1- ) where 0.5 1.

RM x y

Correlation KT KT Closely Related Relation

Relative Relation

ββ

=×

+× ≤≤

(2)

(, ) (, )

where 0 1.

xd yd

Cor r el a t i o n KT KT c os KT KT

TDM x y x y

dyd

cos

∑

•

===

•

∑∑

≤≤

(3)

Here again, Closely Related Relation is

considered as more important than Relative Relation,

since the former has stronger relationship than the

latter. Besides, Closely Related Relation and

Relative Relation can be assigned values according

to the following rules.

(1) Synonym relationship exists between KT

and

Case 1: If KT

is the synonym of KT

, or vice

versa, then Correlation

(KT

, KT

) = 1. e.g., T

the synonym of KT

, and KT

is the same as T

Case 2: otherwise, If KT

and KT

have the same

synonym, then Closely Related Relation

= 1. e.g.,

and KT

have the same synonym T

Key Terms Synonyms …

, T

...

, T

...

(2) Antonym relationship exists between KT

and

Case 1: If KT

is the antonym of KT

, or vice

versa, then Correlation

(KT

, KT

)= 0.5. e.g., T

the antonym of KT

, and KT

is the same as T

Key Terms … Antonyms …

…… ...

…T

, … ...

Case 2: otherwise, If KT

and KT

have the same

antonym, then Closely Related Relation = 1. e.g.,

and KT

have the same antonym T

Key Terms … Antonyms …

… T

… ...

… …, T

...

(3) Relative relationship exists between KT

and

Case 1: If KT

is the relative of KT

, or vice versa,

then Relative Relation

= 1. e.g., T

is the relative of

, and KT

is the same as T

Key Terms … Relatives

… ..., T

,...

… ...

Case 2: otherwise,

Tx Ty

Relative Relation

Tx Ty

∩

∪

where R

and R

are the sets of relatives for KT

and KT

, respectively. e.g., Relative Relation for KT

and KT

as shown below is equal to 3/9.

Key Terms … Relatives

… T

, T

… T

, T

WEBIST 2008 - International Conference on Web Information Systems and Technologies

3.3 Concept Hierarchy Constructor

To generate a concept hierarchy, we first apply a

hierarchical clustering technique to build a binary

clustering tree, and then reorganize the tree into a

taxonomy tree.

3.3.1 Hierarchical Clustering

For the hierarchical clustering algorithm used to

build the binary clustering tree, the clustering

criterion is based on Distance-Matrix transferred

from Correlation-Matrix according to Equation (4).

(, )1 (, ),

where 0 1.

ij ij

Distance KT KT Correlation KT KT

Distance

=−

≤≤

(4)

3.3.2 Reorganizing Binary Clustering Tree

Since each internal node in the binary clustering tree

built using the hierarchical clustering algorithm

contains exactly two children, we would reorganize

the tree into a taxonomy tree to represent a concept

hierarchy. Here, we also use the merging technique

to further reduce the height of the tree where a

threshold is defined as the merging condition. If the

distance between parent and child nodes is less than

the threshold, the child node would be merged into

the parent node. For the example as shown in Fig. 3,

child node N

contains two leaf nodes workflow

modeling and workflow analysis. For the threshold

0.005, since the distance (or gap) between node N

and N

is 0.002, less than the threshold, N

would be

merged into N

. In other words, there is only one

internal node N

left, which contains three leaf nodes

workflow specification, workflow modeling, and

workflow analysis.

Figure 3: Enlarged binary clustering tree.

3.4 Sophisticated Relationship

Extractor

Although both Is-A and Parts-of relationships

between the key terms could be retrieved from

WordNet, only a few words are for Is-A relationships

in the computer science domain in WordNet, and

therefore Wikipedia Categories covering more and

wider words, instead of WordNet, is used to generate

Is-A relationships.

For extracting Is-A relationships, we first label

each key term (or leaf node) in the concept hierarchy

generated beforehand, by finding the categories of

each key term in Wikipedia Categories. As the

example shown in Fig. 4, “Computer hardware

stubs” and “Computer buses” are two categories for

“CompactPCI” and four categories are for “ISA

bus”. Then, each key term in the concept hierarchy

can be labeled. Next, we try to label internal nodes

in the concept hierarchy. Since each internal node

(or cluster) consists of key terms or sub-clusters as

its children, the label should be the least common

categories to cover the children. Therefore, we use

breadth-first search to find the nearest ones among

the common categories in Wikipedia Categories. As

shown in Fig. 4, finding from two categories for

“CompactPCI” and four categories for “ISA bus”,

their least common category would be “Computer

buses”. In Wikipedia Categories, since each term

could have multiple categories, the label for an

internal node might be more than one. By the way, if

the common categories cannot be found or the key

terms do not exist in Wikipedia, some internal nodes

might have no labels. For this case, these internal

nodes are ignored and the process keeps on finding

the least common categories till the root is reached.

For extracting Parts-of relationships, we can

look up a word in WordNet where not only each

sense of the word, but also the relevant domains, is

indicated. Here, the six kinds of Parts-of

relationships of all key terms in WordNet, as

mentioned in Section 2.4, are retrieved as the Parts-

of relationships. During the extraction, we also give

the specified domain to increase the accuracy of

collected Parts-of relationships.

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION

ISA busCompactPCI

Motherboard

expansion slot

IBM hardware

Legacy

hardware

IBM PC

compatibles

Computer buses

Computer

hardware stubs

Motherboard ………………

………

……… ………………

………

Figure 4: Common categories of “CompactPCI” and “ISA

bus” in Wikipedia Categories.

3.5 Ontology Learning

After we construct the ontology for the first time, it

could be gradually refined in the learning phase. The

detailed process of each component in the learning

phase is explained as follows.

(1) Relationship Summary Extractor: The extractor

would extract newly incremental documents as

input, and the terms in the input could be two

types (i.e., existing key terms produced in the

previous phases and completely new index

terms). Both existing key terms and new index

terms are required to create incremental Term-

Document-Matrix, However, only new index

terms are used to create incremental Relative

Matrix.

(2) Correlation Matrix Generator: The generator re-

computes the correlation between each term pair

in different ways, but still using the same

formulas in Section 3.2.2, and then generates

the new correlation matrix. In the learning

phase, both matrices Correlation

TDM

and

Correlation

have some differences from the

ones in the first time computation.

For Correlation

TDM

, it consists of the following

correlations:

1. Existing key terms: they are computed from the

whole vectors, including the former vectors and

the incremental vectors.

2. New index terms: they are computed only from

the incremental vectors extracted from

incremental documents.

3. Existing key terms and new index terms: they are

computed only from the incremental vectors.

For Correlation

, it consists of the following

correlations:

1. Existing key terms: nothing to do.

2. New index terms: they are computed only from

the incremental relative vectors.

3. Existing key terms and new index terms: the

relative vectors of existing key terms and the

incremental relative vectors of new index terms

are used to compute the correlation.

(3) Concept Hierarchy Constructor: The constructor

builds a new concept hierarchy using the new

correlation matrix.

(4) Sophisticated Relationship Extractor: The

extractor retrieves the new Is-A and Parts-of

relationships in the same way.

To maintain the built ontology up-to-date, the

learning process should be executed periodically

(e.g., every six months).

4 IMPLEMENTATIONS

Since there is still no famous ontology on the

computer science domain, the computer science

ontology is constructed as a case study in the

implementation.

4.1 Computer Science Ontology

Construction

In the Relationship Summary Extractor step, we

select 500,000 computing documents with index

terms from the INSPEC database, and 1,848,308

inbuilt index terms are also collected. However,

most of them are not so important or belong to other

domains, so the following filters are used to filter

unsuitable ones.

Since most index terms appear infrequently in all

the documents, only 22,116 index terms appearing

not less than the average are selected as the sample.

In the Correlation Matrix Generator step, 22,116

index terms are merged into 17,350 ones after

stemming, and a correlation matrix is produced.

Finally, for constructing the computer science

ontology, only 10,933 index terms are selected as

the key terms to appear in the ontology through the

filtering process using computing dictionaries, as

shown in Table 1.

Table 1: Number of index terms in each step.

Each step Number of

index terms

Within 500,000 computing

documents

1,848,308

Appearing not less than the

average

22,116

After the stemming process 17,350

In the computer science domain 10,933

WEBIST 2008 - International Conference on Web Information Systems and Technologies

As mentioned in Section 3.2.2, since Relative-

Matrix implies more explicit correlations between

terms than Term-Document-Matrix, α value in

Equation (1) is set as 0.67 (i.e., the former is double

weighting than the latter). For the same reason, β

value in Equation (2) is also set as 0.67. The

statistics of the correlation matrix are presented in

Table 2. Then, we can use the correlation matrix to

construct the computer science ontology.

Table 2: Correlation distributions.

Correlation values Number of correlations

=1.0 10,933

>0&<0.1 3,019,716

>=0.1&<0.2 1,058

>=0.2&<0.3 36,294

>=0.3&<0.4 5,702

>=0.4&<0.5 485

>=0.5&<0.6 4

>=0.6&<0.7 225

>=0.7&<0.8 11

>=0.8&<0.9 0

>=0.9&<1.0 0

Total 3,074,428

In the Concept Hierarchy Constructor step, we

employ the software tool - Matlab to do hierarchical

clustering on Distance-Matrix transferred from

Correlation-Matrix. Furthermore, seven kinds of

methods computing hierarchical clustering are

tested, and then cophenetic correlation coefficient in

Matlab is used to evaluate how well the generated

clustering trees are. The cophenetic correlation for a

clustering tree is defined as the linear correlation

coefficient between the cophenetic distances

obtained from generated clustering trees, and the

original distances (or dissimilarities) used to

construct the tree. In other words, it is a measure of

how faithfully a tree represents the dissimilarities

among observations. The cophenetic correlation

coefficient for each generated clustering tree is

shown in Table 3. For the last three methods,

because of memory limitation, the hierarchical

clustering algorithm cannot generate their

corresponding trees. Finally, since the more the

cophenetic correlation coefficient is and the better

the clustering tree is, we choose the clustering tree

constructed by method unweighted average distance

as the results.

Table 3: Cophenetic correlation coefficients for generated

clustering trees.

Methods Cophenetic correlation

Shortest distance (default) 0.0984

Furthest distance 0.3993

Unweighted average distance 0.4965

Weighted average distance 0.4732

Centroid distance No tree generated

Weighted center of mass

distance

No tree generated

Inner squared distance No tree generated

The gap distribution in the binary clustering tree

is shown as Table 4. We take the threshold 0.005 as

the merging condition, and finally 7,358 clusters are

left to form the concept hierarchy.

Table 4: Gap distribution in the binary clustering tree.

Gap/heig

Merged

clusters

Clusters after

reorganizing

Reduce

ratios

<=0.01 5,381 5,551 0.49222

<=0.005 3,574 7,358 0.32693

<=0.002 2,053 8,879 0.1878

<=0.001 1,362 9,570 0.12459

<=0.0005 887 10,045 0.08114

<=0.0002 523 10,409 0.04784

<=0.0001 331 10,601 0.03028

=0 38 10,894 0.00348

In the Sophisticated Relationship Extractor step,

55 records of Parts-of relationships are extracted

from WordNet, after specifying the computer science

domain (if no specifying, we would have 657

records of Parts-of relationships). For Is-A

relationships, we label each node of the concept

hierarchy using collected categories from Wikipedia

Categories. Finally, 180,681 categories are

collected, and the partial concept hierarchy with Is-A

relationships is shown in Fig. 5.

Memorization

1.Central processing unit

2.Computer data

3.Computer memory

Computing

Workstation

UNIX

workstation

Computer

workstations

Computer

storage

1.Incomplete lists

2.Computer storage devices

3.Rotating disc computer storage media

4.Non-volatile memory

SCSI

Computer

hardware

Computing

………

……… ……… ……… ……… ……… ………

Figure 5: Partial concept hierarchy with Is-A relationships.

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION

4.2 Ontology Web Browsing System

In page Parts-of Relationship, Is-A Relationship, and

Word Relationship of our web browsing system,

users can specify a term to search or browse its

related information, and the results would guide

users through the corresponding website for further

information. As the example shown in Fig. 6, two

different functions such as search and browsing are

provided in page Is-A Relationship, and the next

page lists the result records with hyperlinks guiding

to Wikipedia.

Besides, the browsing system also provides

different search modes to facilitate searching the

built ontology. For example, in the fuzzy search

mode as shown in the left picture of Fig. 6, not only

the input term but also related terms judged by the

correlation matrix are joined to expand the search

scope.

Figure 6: Is-A Relationship page.

5 CONCLUSIONS

In this paper, the proposed framework could be used

to automatically construct domain ontology on a

collection of documents. Although there are some

methods for ontology construction, few of them

could be applied to special documents, such as

academic documents, since very few knowledge

bases can provide features or relationships on the

special terms in such documents. We think our

framework can be used not only on general

documents but also on special ones. Besides, new

incremental documents could be imported to the

framework periodically, and refine the built

ontology in the same way.

Although WordNet can be used to retrieve Parts-

of relationships, there are still not sufficient

relationships for academic terms, especially in a

specific domain such as the computing domain. In

the future, we hope that there will be a thesaurus

with plenty of domain terms and the relationships

between them, thereby improving the built ontology.

Besides, we also hope to define axioms to formalize

the definitions and relations on the built ontology.

REFERENCES

Trent Apted and Judy Kay, 2002. “Automatic construction

of learning ontologies,” Proc. ICCE Workshop on

Concepts and Ontologies in Web-based Educational

Systems, pp. 1563-1564.

Florian Beil, Martin Ester, and Xiaowei Xu, 2002.

“Frequent term-based text clustering,” Proc. 8

ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining, pp. 436-442.

Richard C. Bodner and Fei Song, 1996. “Knowledge-

based approaches to query expansion in information

retrieval,” Proc. 11

Biennial Conference of the

Canadian Society for Computational Studies of

Intelligence on Advances in Artificial Intelligence, pp.

146-158.

P. Buitelaar, P. Cimiano, and B. Magnini, 2005. Ontology

Learning from Text: Methods, Evaluation and

Applications, Frontiers in Artificial Intelligence and

Applications Series, Vol. 123.

Rowena Chau and Chung-Hsing Yeh, 2005. “Enabling a

semantic smart WWW: a soft computing framework

for automatic ontology development,” Proc.

International Conference on Intelligent Agents, Web

Technologies and Internet Commerce, pp. 1067-1071.

Michael Dittenbach, Dieter Merkl, and Andreas Rauber,

2000. “The growing hierarchical self-organizing map,”

Proc. the International Joint Conference on Neural

Networks, Vol. 6, pp. 15-19.

Dave Elliman and JRG Pulido, 2001. “Automatic

derivation of on-line document ontologies,” Proc.

International Workshop on Mechanisms for Enterprise

Integration: From Objects to Ontologies (MERIT

2001), the 15

European Conference on Object

Oriented Programming.

W. B. Frakes and R. Baeza-Yates, 1992. Information

Retrieval: Data Structures and Algorithms, Prentice

Hall.

Weipeng Fu, Bin Wu, Qing He, and Zhongzhi Shi, 2001.

“Text document clustering and the space of concept on

text document automatically generated,” Proc. IEEE

ICII Conference, Vol. 3, pp. 107-112.

K. W. Gan, C. Y. Wang, and Brian Mak, 2002.

“Knowledge-based sense pruning using the HowNet:

an alternative to word sense disambiguation,” Proc.

International Symposium of Chinese Spoken

Language Processing, pp. 189-192.

Asunción Gómez-Pérez and David Manzano-Macho, 2003.

“A survey of ontology learning methods and

techniques,” OntoWeb Deliverable 1.5.

Yi Guan, Xiao-Long Wang, Xiang-Yong Kong, and Jian

Zhao, 2002. “Quantifying semantic similarity of

Chinese words from HowNet,” Proc. International

WEBIST 2008 - International Conference on Web Information Systems and Technologies

Conference on Machine Learning and Cybernetics,

Vol. 1, pp. 234-239.

Yin-Fu Huang and Chun-Hao Hsu, 2007. “PubMed

smarter: searching the papers with implicit words

based on Gene Ontology,” Proc. 4

International

Conference on Information Technology and

Applications, Vol. 1, pp. 339-343.

Sin-Jae Kang and Jong-Hyeok Lee, 2001. “Semi-

automatic practical ontology construction by using a

thesaurus, computational dictionaries, and large

corpora,” Proc. Workshop on Human Language

Technology and Knowledge Management, pp. 1-8.

M. Kavalec, A. Maedche, and V. Svatek, 2004.

“Discovery of lexical entries for non-taxonomic

relations in ontology learning,” SOFSEM 2004:

Theory and Practice of Computer Science, LNCS

2932, pp. 249-256.

Latifur Khan and Lei Wang, 2002. “Automatic ontology

derivation using clustering for image classification,”

Proc. Workshop on Multimedia Information Systems,

pp. 56-65.

Teuvo Kohonen, Samuel Kaski, Krista Lagus, Jarkko

alojärvi, Jukka Honkela, Vesa Paatero, and Antti

Saarela, 2000. “Self-organization of a massive

document collection,” IEEE Transactions on Neural

Networks, Vol. 11, No. 3, pp. 574-585.

Yan-Hwang Kuo, Chang-Shing Lee, Shu-Mei Guo, and

YingHsu Chen, 2005. “Apply object-oriented

technology to construct Chinese ontology on the

internet,” Journal of Internet Technologies, Vol. 6, No.

4, pp. 385-394.

Jim Z. C. Lai and Wen-Feng Wu, 2002. “Design and

implementation of a classifier for Chinese e-mails,”

Proc. 7

Conference on Artificial Intelligence and

Applications, pp. 368-373.

Alexander Maedche and Steffen Staab, 2000. “Mining

ontologies from text,” Proc. 12

European Workshop

on Knowledge Acquisition, Modeling and

Management, pp. 189-202.

Alexander Maedche and Steffen Staab, 2001. “Ontology

learning for the semantic web,” IEEE Intelligent

Systems, Vol. 16, No. 2, pp. 72-79.

Riichiro Mizoguchi, 2003. “Tutorial on ontological

engineering - part 1: introduction to ontological

engineering,” New Generation Computing, Vol. 21,

No. 4, pp. 365-384.

Thanh Tho Quan, Siu Cheung Hui, and Tru Hoang ao,

2006. “Automatic fuzzy ontology generation for

semantic web,” IEEE Transactions on Knowledge and

Data Engineering, Vol. 18, No. 6, pp.842-856.

Prieto-Diaz Ruben, 2003. “A faceted approach to building

ontologies,” Proc. IEEE International Conference on

Information Reuse and Integration, pp. 458-465.

David Sánchez and Antonio Moreno, 2006. “Discovering

non-taxonomic relations from the web,” Proc. 7

International Conference on Intelligent Data

Engineering and Automated Learning, pp. 629-636.

A. Schutz and P. Buitelaar, 2005. “RelExt: a tool for

relation extraction in ontology extension,” Proc. 4

International Semantic Web Conference, pp. 593-606.

Vaclav Snase, Pavel Moravec, and Jaroslav Pokorny, 2005.

“WordNet ontology based model for web retrieval,”

Proc. International Workshop on Challenges in Web

Information Retrieval and Integration, pp. 220-225.

Yuri A. Tijerino, David W. Embley, Deryle W. Lonsdale,

and George Nagy, 2003. “Ontology generation from

tables,” Proc. 4

International Conference on Web

Information Systems Engineering, pp. 242-249.

Ju-in Youn, He-Jue Eun, Cheol-Jung Yoo, and Yong-Sung

Kim, 2004. “Adaptive documents classification system

based on ontology constructed by fuzzy function and

fuzzy relations,” Proc. International Conference on

Cyberworlds, pp. 182-187.

A FRAMEWORK AUTOMATING DOMAIN ONTOLOGY CONSTRUCTION