BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML

STREAMS

Stefan Böttcher, Rita Hartel and Christian Heinzemann

University of Paderborn, EIM - Electrical Engineering, Computer Science and Mathematics

Fürstenallee 11, 33102 Paderborn, Germany

Keywords: XML compression, XML data streams.

Abstract: XML data compression is an important feature in XML data exchange, particularly when the data size may

cause bottlenecks or when bandwidth and energy consumption limitations require reducing the amount of

the exchanged XML data. However, applications based on XML data streams also require efficient path

query processing on the structure of compressed XML data streams. We present a succinct representation of

XML data streams, called Bit-Stream-Based-Compression (BSBC) that fulfills these requirements and addi-

tionally provides a compression ratio that is significantly better than that of other queriable XML compres-

sion techniques, i.e. XGrind and DTD subtraction, and that of non-queriable compression techniques like

gzip. Finally, we present an empirical evaluation comparing BSBC with these compression techniques and

with XMill that demonstrates the benefits of BSBC.

1 INTRODUCTION

1.1 Motivation

XML is widely used in business applications and is

the de facto standard for information exchange in

fixed wired networks. Because of the verbose struc-

ture of XML, applications operating on continuous

XML data streams or requiring very large amounts

of XML data will likely benefit from XML compres-

sion techniques in platforms such as mobile net-

works where storage, bandwidth or energy are lim-

ited for the following reason. Applications save

energy and processing time not only when loading

compressed instead of uncompressed XML data, but

also they can execute path queries directly on the

compressed data format, i.e., without decompressing

it. We propose an XML compression technique,

called Bit-Stream-Based-Compression (BSBC),

which supports path queries while achieving in our

experiments a better compression ratio than other

XML compression techniques for XML data streams

which support path queries, i.e. XGrind and DTD

subtraction. Furthermore, BSBC achieves an even

better compression ratio than text compression tools

like gzip, and it sometimes even beats XMill.

1.2 Contributions

This paper proposes a novel approach to XML com-

pression, called Bit-Stream-Based-Compression

(BSBC) that combines the following properties:

• It removes redundancies within the structure

of the XML file by sharing identical sub-trees

• It separates an XML data stream into its con-

stituent parts: its tree structure extended by

pointers to common sub-trees, its names of ele-

ments and of attributes, and its values of text

constants and of attributes.

• It compresses the tree structure to a bit stream

and a sub-tree pointer stream, it collects bit

stream positions of names of elements and at-

tributes in inverted lists, and it groups structur-

ally related text and attribute values into con-

tainers to improve the compression ratio.

• It stores compressed data into packages allow-

ing thus shorter relative addresses in inverted

lists and value containers.

• It combines a fast bit stream-based navigation

technique along the child, descendant, follow-

ing-sibling, and following axes with direct ac-

cess to elements and attributes via inverted

lists. As the navigation along these axes can be

Böttcher S., Hartel R. and Heinzemann C. (2008).

BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML STREAMS.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 13-21

DOI: 10.5220/0001518000130021

 SciTePress

done on the bit stream alone, it needs a mini-

mum of space and can be done very fast.

• Combined with a preliminary step, which re-

writes queries containing backward axes into

equivalent queries containing only on forward

axes, BSBC allows fast navigation along all

XML axes.

As a result, BSBC has the following advantages.

In comparison to other approaches to path queries on

XML streams (e.g. AFilter (Candan et al., 2006))

that support only some axes and that require decom-

pression to process queries, BSBC supports the exe-

cution of path queries involving all XML axes, and

it does not require decompression for the purpose of

path query processing. Furthermore, our extensive

evaluation demonstrates that the compression ratio

achieved by BSBC outperforms that of other XML

compression techniques (like XGrind and DTD sub-

traction) that support path queries. To the best of our

knowledge, there is no other XML compression sys-

tem that combines the advantages of BSBC.

1.3 Paper Organization

The remainder of this paper is organized as follows.

Section 2 describes how a SAX stream is com-

pressed by two compression steps each of which

transforms an input data stream into two or three

compressed output data streams, and it explains how

the document structure is stored in a sub-tree pointer

stream and in a bit stream and separated from the

elements and attributes which are stored in inverted

lists. Section 3 describes how to implement naviga-

tion along the XML axes and extended navigation

on the bit stream, the sub-tree pointer stream, and

the inverted lists. Section 4 compares the compres-

sion ratio of BSBC with that of other approaches.

Section 5 compares BSBC to related work. Finally,

Section 6 summarizes our contributions.

2 THE STREAMS

– KEY OF OUR SOLUTION

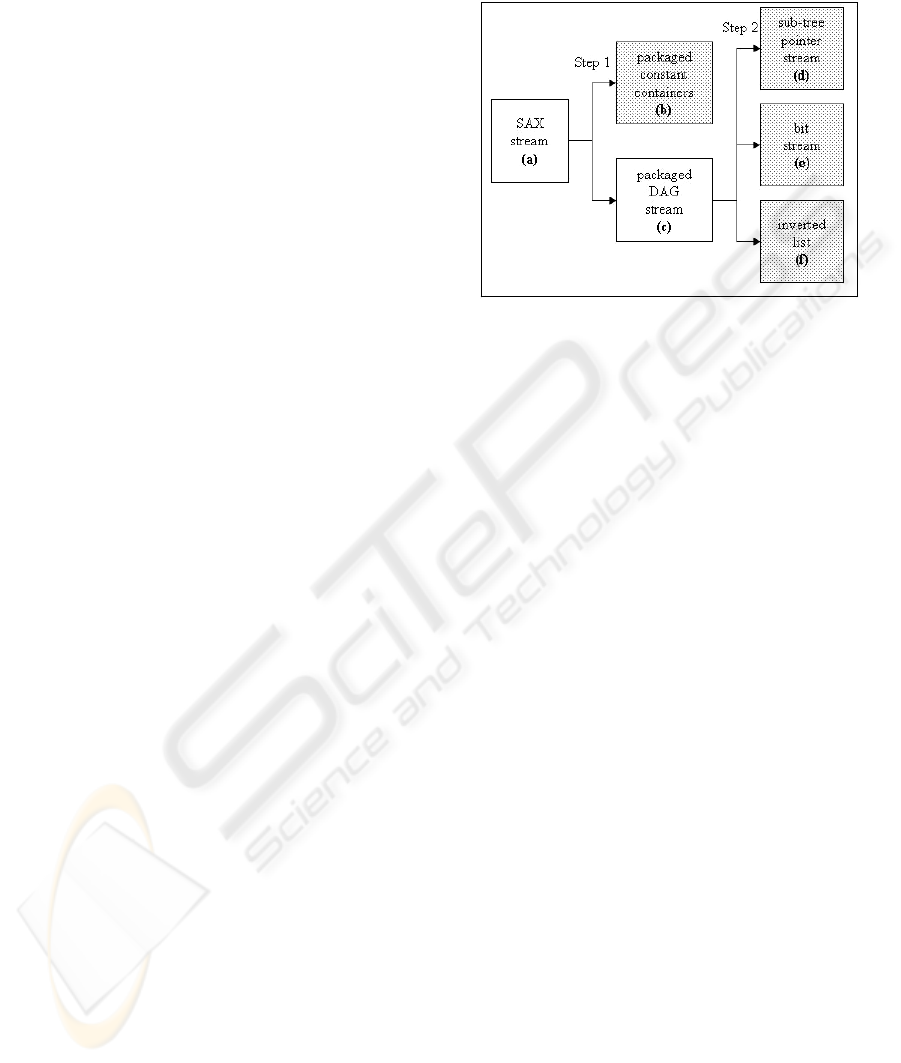
BSBC views XML data as an input stream of SAX

events that is transformed by two steps into four

other streams (c.f. Figure 1).

Step 1 transforms the SAX stream (a) into con-

stant containers (b) and an intermediate binary DAG

stream (c), which is in Step 2 transformed into a

sub-tree pointer stream (d) representing the back-

ward pointers to shared sub-trees within the DAG, a

bit stream (e) capturing the tree structure of the

XML data, and an inverted list (f), containing a

mapping from element names to positions within the

bit stream.

Figure 1: Compression Steps of the BSBC system.

2.1 Step 1: Separating XML into DAG

Packages and Constant Containers

As we expect a significantly higher repetition ratio

for element and attribute names than for constants,

we first separate element and attribute names from

constants, and we then use a different technique for

the compression of element and attribute names than

we use for the compression of constants.

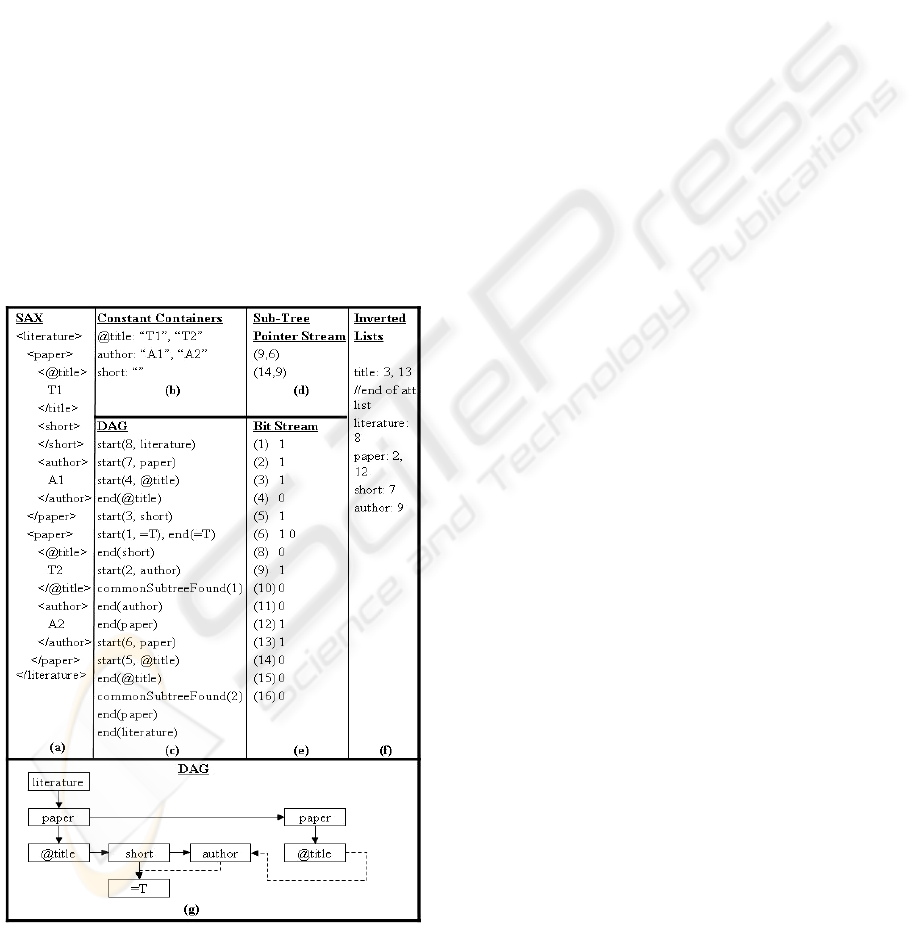
Step 1 is done as follows (for an example see

Figure 2). The input SAX stream (Figure 2(a)) is

parsed and separated into a stream of two different

kinds of packages: packages of constant containers

(Figure 2(b)), which contain the constants, i.e., the

text and attribute values of the SAX stream, and

DAG packages which contain the XML structure.

Figure 2(g) shows a graphical representation of the

binary DAG of the SAX stream of Figure 2 (a), i.e.,

all text nodes have been replaced with “=T” and

common binary sub-trees are shared, and Figure 2(c)

shows the DAG package generated from the SAX

stream.

The DAG packages are constructed by a DAG

processor like e.g. the one presented in (Böttcher

and Steinmetz, 2007) and consist of the following

kinds of events: startElement(id, label) and endEle-

ment(id, label), which are similar to the correspond-

ing SAX events, but which contain an additional,

unique node ID, and the additional event common-

SubtreeFound(id) which represents a backward

pointer to the sub-tree rooted by the node with ID id.

The structure-oriented SAX events, i.e., start-

Document, startElement, endElement, and endDocu-

ment, are passed to the DAG compressor. Hereby

the attributes are treated as follows: An attribute

WEBIST 2008 - International Conference on Web Information Systems and Technologies

definition of the form att=“value” is passed as an

event sequence startElement(“@att”), endEle-

ment(“@att”), which is sent to the DAG compres-

sor, whereas the pair (@att, value) is passed to the

constant containers and will be processed later.

Whenever a character-event is received, an event

sequence startElement(“=T”), endElement(“=T”) is

sent to the DAG compressor, and the pair (element,

value) is passed to the constant containers, where

element is the label of the parent node of the text

node.

However, if an event startElement(“E1”) is di-

rectly followed by an event endElement(“E1”) in

the SAX stream, i.e., if an empty element tag is

found, this is treated like a character-event receiving

an empty text node. That is, an event sequence star-

tElement(“=T”), endElement(“=T”) is sent to the

DAG compressor, and the pair (E1, “”) is passed to

the constant containers, where “” is the empty con-

stant. This is done to ensure that all leaf nodes are

either constants, which are represented by “=T”, or

attribute nodes, which are represented by a name

starting with ‘@’.

Figure 2: (a) SAX stream, (b) constant containers, (c) bi-

nary DAG stream, (d) sub-tree pointer stream, (e) bit

stream, (f) inverted lists of our example, and (g) graph of

the binary DAG.

For the storage of constants, we follow the idea pre-

sented in XMill (Liefke and Suciu, 2000) and sort

the constants according to their parent element into

separate data containers (i.e., the @title container,

the author container, and the short container in Fig-

ure 2(b)). Each container for constants with a parent

element Ei stores the text values included in Ei ele-

ments in the order in which they occur in the docu-

ment. Each container is then compressed using

BZip2 which implements Burrows-Wheeler Block-

Sorting (Burrows and Wheeler, 1994) followed by

Huffman-Encoding (Huffman, 1952).

In order to support (unbounded) XML streams,

we divide both structures (DAG and constants) into

packages: Whenever a certain number n of events

was received, the DAG that was compressed so far,

the path of non-compressed nodes (i.e., the nodes

from root to the current node, the next-siblings of

which were not yet inserted into the DAG), and the

compressed constant containers are passed to the

second step. This allows a pipelined approach that is

capable to compress (unbounded) XML data

streams.

2.2 Step 2: Transforming DAG

Packages into Multiple Streams

During decompression or query processing, we have

to correctly recombine element and attribute names

with included constants, i.e., we have to know the

correct relative positions of both kinds of data. For

this purpose, we generate the so called bit stream

during compression.

Within Step 2, we use the DAG stream for gen-

erating three new streams as follows. We separate

element names from the structure of the DAG

stream (Figure 2(c)), i.e., we transfer names to a

separate stream, called inverted lists (Figure 2(f)) to

hold the names of elements or their attributes. The

remaining structure of the DAG stream is stored in

the bit stream (Figure 2(e)) and the sub-tree pointer

stream (Figure 2(d)). These three streams together

enable the traversal of the XML document without

requiring decompression.

2.2.1 The Bit Stream and the Sub-tree

Pointer Stream

The bit stream simply contains a “1”-bit for each

event startElement of the DAG stream, and a “0”-bit

for each event endElement of the DAG stream.

In an intermediate table, a mapping from node

IDs to positions of the corresponding ‘1’-bit within

the bit stream is stored. Whenever a commonSub-

BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML STREAMS

treeFound(id)-event is read, the position pID of the

node with ID id is looked up, and the pair (current-

Pos, pID) representing the sub-tree pointer is written

to the sub-tree pointer stream, where currentPos is

the current position within the bit stream.

2.2.2 The Inverted Lists

In order to store the mapping of element names to

positions within the bit stream, BSBC uses inverted

lists, where each element name occurring in the

package is associated with a list of relative addresses

(N1,N2,…) where the elements with this element

name occur.

Each element name is thus stored only once per

package within the inverted list, regardless of how

often it occurs in the XML data. As furthermore no

additional pointers are needed, this succinct repre-

sentation of elements and their positions can sig-

nificantly save space.

While parsing the DAG stream, whenever re-

ceiving an event startElement(id, “E1”), a ‘1’-bit is

inserted into the bit stream (as described above), but

at the same time, the position P of the new ‘1’-bit

within the bit stream is written to the inverted ele-

ment list of the element E1.

This will be useful for the typical XPath location

steps /E1 and //E1 as outlined in Section 3. In the

rare case where the element name of an element at a

specific position N, say N=10, is needed, it is still

possible to search N in the sorted list of each ele-

ment E until the position N is found or until a num-

ber >N indicates that N will not occur in the sorted

list of positions of E elements.

Furthermore, it is possible to sort the inverted

lists within each package such that the entries for all

attribute names precede the entries for all elements.

This makes unnecessary all the “@”-characters used

as a prefix for each attribute name. Instead, all the

“@”-characters can be replaced by a single pointer

per package to the first inverted list of an element.

In order to reach a better compression result, we

do not repeat each element name in each package.

Instead, we define a symbol SE1 for an element

name E1 the first time it occurs in the compressed

data. And we replace each further occurrence of E1

in the following packages by its symbol SE1.

The inverted element list for the text nodes, i.e.,

the inverted element list for the element “=T” is not

stored in the final compressed data, as each ‘1’-bit

position that is not included in any inverted element

list has to be a text node.

2.3 Optimizing Query Evaluation by

Sparse Constant Pointers

Within the evaluation of path queries, we will have

to find a constant T for a given position P within the

bit stream that represents the placeholder “=T” for T.

With the help of the element label “E1” of the parent

of T, we can identify the correct constant container

CE1, but in order to identify the correct position of T

within CE1, we have to know, how many nodes with

label “=T” and with a parent node with label “E1”

exist up to the current context node.

Without any additional information, we would

have to count these nodes from the start of the docu-

ment, i.e., we would not be able to skip parts of the

compressed document during query evaluation.

In order to avoid this disadvantage, we attach to

every d-th bit D in the bit stream the information of

how many nodes with label “=T” and with a parent

node with label “E” exists up to D for each element

label E that has occurred within the document so far.

3 NAVIGATION ON THE

STREAMS

Each navigation step can start at the bit-stream posi-

tion P

start

of the start-element tag of an arbitrarily

chosen current context node C. We first explain ba-

sic navigation steps, and then use them to compose

more complex navigation steps on the compressed

XML data.

3.1 Basic Navigation using the

First-attribute, First-child and

Next-sibling Axes

Given the bit-stream position P

start

of the current

context node C, many navigation steps, e.g., finding

C’s next–sibling, requires finding the bit-stream po-

sition P

end

of C’s end-element tag.

3.1.1 Finding the Position P

end

of the

End-tag

In order to proceed to the bit stream position P

end

the “0”-bit in the bit stream that represents the end-

tag of the current context node, each start-tag has to

be closed by exactly one end-tag, i.e., we search the

corresponding “0”-bit for each “1”-bit on the bit

stream as follows. The search counts “0”-bits and

“1”-bits, starts at the bit stream position P

start

, and

continues counting bits of the bit-stream until the

WEBIST 2008 - International Conference on Web Information Systems and Technologies

number of “1”-bits is equal to the number of “0”-

bits, i.e., each start-tag has been closed.

end

may occur in a later package than P

start

. Note

that nevertheless, we can use relative addresses for

start

and P

end

because the operation ‘find position

end

of the corresponding end tag’ operates on the bit

streams only, i.e., searching for P

end

in the bit stream

of a later package does not disturb the use of small

relative addresses.

3.1.2 Proceeding to the Next-sibling

In order to find the bit stream Position PNS

start

of the

bit that tells us whether or not the current context

node has a next sibling, we first proceed to the posi-

tion P

end

of the “0”-bit in the bit stream that repre-

sents the end-tag of the current context node. The bit

at position P

end

+1, i.e., after the bit representing the

end-tag, is a “1”-bit representing the next-sibling if a

next-sibling exists, and a “0”-bit otherwise.

3.1.3 Distinguishing Elements and

Attributes from Text Constants

The current context node represented by a “1”-bit at

position P

start

in the bit-stream is an element name if

the node is an inner node, i.e., if the next bit stream

position P

start

+1 also contains a “1”-bit. However, if

the next bit stream position P

start

+1 contains a “0”-

bit, the current context node represented by the “1”-

bit at position P

start

is a leaf node, i.e., it either is a

constant, or it is an attribute name. It is a constant, if

and only if P

start

can not be found in any inverted list

of an attribute name.

3.1.4 Determining Element Names and

Attribute Names and Distinguishing

Elements from Attributes

Which name the element or attribute of the current

context node C has, can be distinguished by search-

ing position P

start

in the inverted lists. C is an attrib-

ute or an element, depending on in which kind of an

inverted list P

start

is found. Inverted lists for attributes

are distinguished from inverted lists for elements by

grouping inverted lists in each package and by pro-

viding a pointer to the first inverted list of an ele-

ment for each package.

3.1.5 Proceeding to the First-attribute Node

Let P

start

be the bit stream position of an element

node C. C has a first-attribute if and only if bit

stream position P

start

+1 contains a “1”-bit and repre-

sents an attribute. In this case, P

start

+1 represents C’s

first-attribute.

3.1.6 Proceeding to the First-child Node

In order to find the bit stream Position PFC

start

of the

bit that tells us whether the current context node has

a first-child, we have to proceed similar as when

searching for the first-attribute, except that whenever

a “1”-bit represents an attribute instead of the first-

child, we use the bit stream to proceed to the attrib-

ute’s next-sibling.

The attribute’s next-sibling is ei-

ther the next attribute, in which case we continue to

search for a next-sibling or it is the first-child or it

does not exist, which means that there is no first-

child.

3.2 Navigation using the other Forward

Axes

Given a position P

start

of the start-tag of the current

context node, we first determine the position P

end

the end-tag of the current context node as explained

before. The next step depends on the forward axis to

be used.

3.2.1 Proceeding to Descendant-or-Self::E1

When a location step //E1 requires searching a de-

scendant-or-self E1 element, the search is signifi-

cantly easier than standard path search for a de-

scendant-or-self E1. Only E1 elements with a bit

stream position PE1

start

in the interval of [P

start

, P

end

)

fulfill the descendant-or-self condition. Therefore, in

the packages that match these addresses

, we simply

lookup the inverted lists for E1 in order to find the

bit stream positions PE1

start

of E1 descendant nodes

with P

start

≤ PE1

start

< P

end

3.2.2 Proceeding to Child::E1 or to

Attribute::A1

When we search a child::E1 or an attribute @A1 re-

spectively, we use the inverted lists of E1 or @A1 in

all relevant packages to look for positions PE1

start

with P

start

< PE1

start

< P

end

, and we use the bit streams

to check that the depth of PE1

start

is exactly one more

This is where we find the first-child because further attributes of

C are stored as siblings of the first-attribute and the first-child is

stored as the ‘next-sibling’ of the last attribute in our simple ele-

ment stream.

We use PE1

start

end

as a shortcut for ‘P

end

belongs to a later

package than PE1

start

or they belong to the same package and

PE1

start

is less than P

end

’.

BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML STREAMS

than the depth of P

start

, i.e., the number of “1”-bits is

exactly one more than the number of “0”-bits in the

bit stream interval from P

start

to PE1

start

. These posi-

tions PE1

start

represent the element start-tags for the

child::E1 elements or the attributes @A1 that we are

looking for.

3.2.3 Proceeding to Following-sibling::E1

When we search a following-sibling::E1, we addi-

tionally lookup the bit stream position PP

end

of the

end-tag of the parent of current context node. PP

end

is the first bit stream position after P

end

where the

number of “0”-bits exceeds the number of “1”-bits

by one.

Then, we use the inverted lists of E1 in all rele-

vant packages to look for positions PE1

start

with P

end

< PE1

start

< PP

end

, and we use the bit streams to

check that the depth of PE1

start

is the same as the

depth of P

start

, i.e., the number of “1”-bits is equal to

the number of “0”-bits in the bit stream interval from

start

to PE1

start

. These positions PE1

start

represent the

element start-tags for the following-sibling::E1 ele-

ments that we are looking for.

3.2.4 Proceeding to Following::E1

Finally, when we search a following::E1, we use the

inverted lists of E1 to look for positions that are lar-

ger than P

end

or occur in a later package.

3.2.5 Looking-up a Specific Constant

When searching a constant V for a given position X

within the bit stream, we also regard the parent ele-

ment – or parent attribute in the case of attribute

values – E of V in the bit stream.

As described in Section 2.3, we have attached pe-

riodically sparse constant pointers to bit stream posi-

tions that define, how many text values V’ for a

given parent element or parent attribute E’ have

been parsed so far.

In order to search the text value for a given posi-

tion X, we have to go back within the bit stream to

the last constant pointer, i.e., to the last bit stream

position C that contains the text container offset and

lookup the offset O for the parent element – or par-

ent attribute – E. Afterwards, we start there to count

the number N of text nodes that have the parent ele-

ment – or parent attribute – E. This has to be done in

consideration of the sub-tree pointers as described in

Section 3.3. As some of the elements might contain

mixed mode, we have to consider, that one element

may not only contain a single text node as child, but

as well two or more.

The text value that we are looking for, can then

be found as the O+Nth text value within the constant

container of the element – or attribute – E.

3.3 Sub-tree Pointers

So far, we did not handle the sub-tree pointers stored

within the sub-tree pointer stream. Whenever we

reach a position p within the bit stream for which an

entry (p, pID) exists within the sub-tree pointer

stream, we store the position p on a stack and con-

tinue to parse the bit stream at position pID. When

the end of the sub-tree started at pID is reached, i.e.,

when we have read as many ‘1’-bits as ‘0’-bits, we

jump back to the position which is given on top of

the stack and remove this position from stack.

3.4 Backward Axes

We do not explicitly consider backward axes here,

as it is possible to rewrite each XPath query using

backward axes into an equivalent XPath query using

forward axes only. An approach on how to rewrite

backward axes is presented in (Olteanu et al., 2002).

4 EVALUATION OF THE

COMPRESSION

We have implemented BSBC using Java 1.5 and a

SAX parser for parsing XML documents. We have

evaluated BSBC on the following datasets:

1. XMark(XM) – an XML document that models

auctions (Schmidt et al., 2002)

2. hamlet(H) – an XML version of the famous

Shakespeare play

3. catalog-01(C1), catalog-02(C2), dictionary-01

(D1), dictionary-02(D2) – XML documents that

were generated by the XBench benchmark (Yao

and Özsu, 2002)

4. dblp(DB) – a bibliographic collection of publica-

tions

As can be seen in Table 1, the sizes of the docu-

ments reach from a few hundred kilobytes to more

than 300 Megabytes.

Table 1: Sizes of documents of our dataset.

document XM H C1 C2 DB D1 D2

Uncom-

pressed

size in MB

5.3 0.3 10.6 105.3 308.2 10.8 106.4

WEBIST 2008 - International Conference on Web Information Systems and Technologies

We compared BSBC with four other approaches:

- XGrind (Tolani and Hartisa, 2002) – a queryable

XML compressor

- gzip – a widely used text compressor

- XMill (Liefke and Suciu, 2000) – an XML com-

pressor using BZip2 for the compression of con-

stant values

- DTD subtraction (Böttcher, Steinmetz, and Klein,

2007) – a DTD-conscious XML compressor using

gzip for the compression of constant values that al-

lows query evaluation and partial decompression

During our experiments, we have chosen d=100, i.e.,

each 100

bit contains direct pointers into the con-

stant containers.

20%

40%

60%

gzip

33% 28% 21% 21% 18% 30% 30%

XMill

22% 21% 10% 10% 11% 18% 18%

XGrind

46% 32% 32% 54% 54%

DTDSub.

32% 34% 17% 17% 22% 29% 29%

BSBC

24% 22% 9% 9% 12% 18% 18%

XM H C1 C2 DB D1 D2

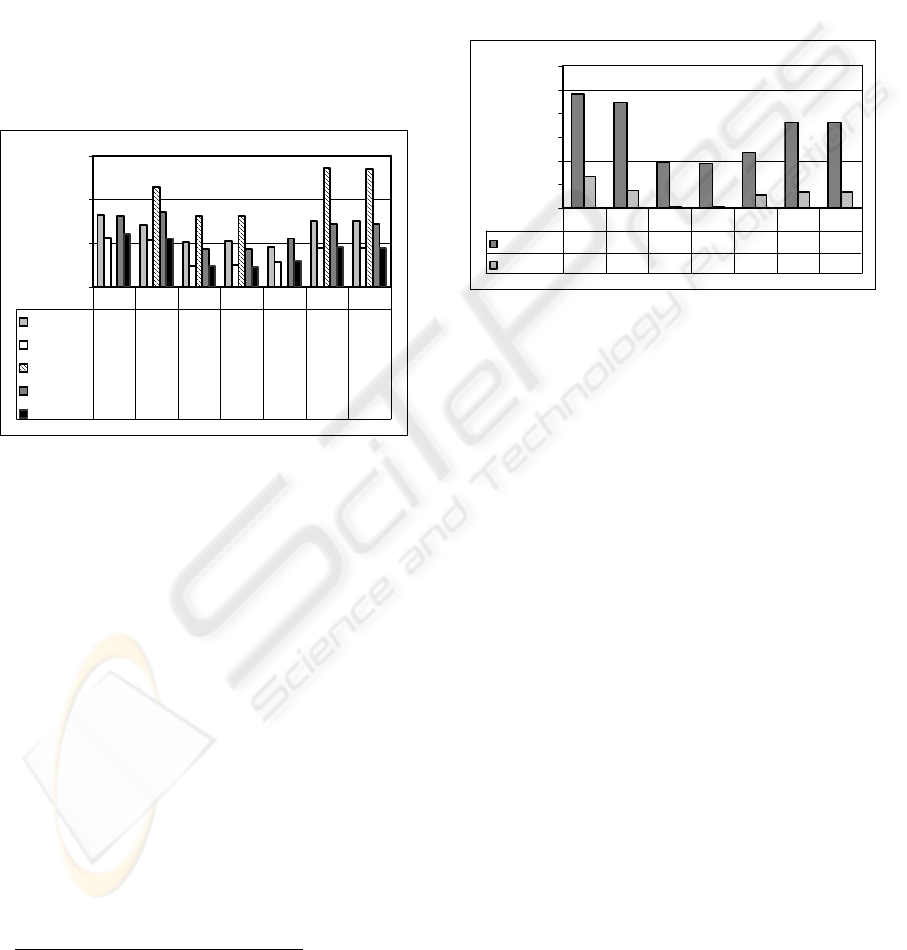
Figure 3: Compression ratio of the whole XML document.

The results of our experiments are shown in Figure

3. Using these datasets, XMill performs better for

XM, H, DB, D1 and D2 achieving compression ra-

tios that are up to 2% lower than those of BSBC,

whereas BSBC performs better for C1 and C2

achieving compression ratios that are up to 1%

lower than those of XMill. However, in contrast to

XMill, BSBC allows to evaluate queries on the com-

pressed data and to decompress data only partially.

Our approach, BSBC, performs significantly bet-

ter than gzip, and has the additional advantage over

gzip that query processing can be performed effi-

ciently directly on the compressed data. The im-

provements in compression ratios over gzip range

from 6% to 12%.

Compared to XGrind – an approach that allows

efficient query evaluation and partially decompres-

sion – our approach, BSBC, achieves a higher com-

pression ratio

. The difference of the compression

Note that on our test computer, we got access violations when

running XGrind on XM and DB and therefore the compression

ratios for these two documents are missing

ratios (XGrind minus BSBC) range from 24% to

36%.

Compared to DTDsubtraction, BSBC achieves a

higher compression ratio. The differences of the

compression ratios (DTDsubtraction minus BSBC)

range from 8% to 11%.

In a second series of measurements, we have

measured the size of the structure compression, i.e.,

the constant containers were removed from the com-

pressed data. The results of these experiments are

shown in Figure 4.

10%

15%

20%

25%

30%

Total

24% 22% 9% 9% 12% 18% 18%

Structure

6.5% 3.5% 0.3% 0.2% 2.6% 3.3% 3.3%

XM H C1C2DB D1D2

Figure 4: Structure compression compared to total com-

pression.

Our experiments have shown that especially the

structure compression of BSBC is extremely high.

While the total compression reaches a ratio of 9% to

24%, the structure compression ranges from 0.2% to

6.5%. The structure compression is up to 40 times

stronger than the total compression for C1, in gen-

eral it is at about 5 times stronger than total com-

pression.

5 RELATED WORK

There exist several XML compression approaches,

which can be mainly divided into three categories.

First, approaches that avoid redundancies within the

string values (of element and attribute names as well

as of constants) by using dictionaries and tokeniza-

tion. Second, approaches that avoid redundancies

within the structure, i.e., that avoid multiple occur-

rences of complete sub-trees within the XML docu-

ment tree. Finally, approaches that avoid redundan-

cies that occur when schema information is known.

All these approaches differ in their features, particu-

larly in whether the compressed data structures can

be decompressed partially, whether the compressed

data structures are queriable, and whether they sup-

port unbounded XML data streams.

BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML STREAMS

The last category (avoiding external redundan-

cies given by schema information) includes such ap-

proaches as XCQ (Ng et al., 2006) and DTD sub-

traction (Böttcher, Steinmetz, and Klein, 2007).

They both separate the structural information from

the textual information and then subtract the given

schema information from the structural information.

Instead of a complete XML structure stream or tree,

they only generate and output information not al-

ready contained in the schema information (e.g., the

chosen alternative for a choice-operator or the num-

ber of repetitions for a *-operator within the DTD).

Both approaches, XCQ and DTD subtraction, are

queriable and applicable to XML streams, but they

can only be used if schema information is available.

XQzip (Cheng and Ng, 2004) and the approach

presented in (Buneman, Grohe, and Koch, 2003) be-

long to the second category (avoiding structural re-

dundancies). They compress the data structure of an

XML document bottom-up by combining identical

sub-trees. Afterwards, the data nodes are attached to

the leaf nodes, i.e., one leaf node may point to sev-

eral data nodes. The data is compressed by an arbi-

trary compression approach. These approaches allow

querying compressed data, but they are not directly

applicable to infinite data streams.

An extension of (Buneman, Grohe, and Koch,

2003) and (Cheng and Ng, 2004) is the BPLEX al-

gorithm (Busatti, Lohrey, and Maneth, 2005). This

approach does not only combine identical sub-trees,

but recognizes patterns within the XML tree that

may span several levels, and therefore allows a

higher degree of compression. In comparison to

BSBC, this approach does not explicitly define how

to compress text constants and attribute values con-

tained in XML data and how to distinguish both in

the compressed XML format.

The first category (avoiding textual redundancies

by tokenization) allows for a much faster compres-

sion approach than the second one, as only local data

has to be considered in the compression as opposed

to considering different sub-trees as in the second

category.

The XMill algorithm (Liefke and Suciu, 2000) is

an example of the first category. It compresses the

structural information separately from the data. Data

is grouped according to its enclosing element and

collected into several containers, and each container

is compressed afterwards. The structure is com-

pressed, by assigning each tag name a unique and

short ID. Each end-tag is encoded by the symbol ‘/’.

This approach does not allow querying the com-

pressed data.

XGrind (Tolani and Hartisa, 2002), XPRESS

(Min, Park, and Chung, 2003) and XQueC (Arion et

al., n.d.) are extensions of the XMill-approach. Each

of these approaches compresses the tag information

using dictionaries and Huffman-encoding (Hufman,

1952) and replaces the end-tags by either a ‘/’-sym-

bol or by parentheses. All three approaches allow

querying the compressed data, and, although not ex-

plicitly mentioned, they all seem to be applicable to

data streams.

Approaches (Bayardo et al., 2004), (Cheney,

2001), and (Girardot and Sunderesan, 2000) are

based on tokenization. (Cheney, 2001) replaces each

attribute and element name by a token, where each

token is defined the first time it is used. (Bayardo et

al., 2004) and (Girardot and Sunderesan, 2000) use

tokenization as well, but they enrich the data by ad-

ditional information that allows for a fast navigation

(e.g., number of children, pointer to next-sibling, ex-

istence of content and attributes). All three of them

use a reserved byte to encode the end-tag of an ele-

ment. They are all applicable to data streams and al-

low querying the compressed data.

The approach in (Ferragina et al., 2006) does not

belong to any of the three categories. It is based on

Burrows-Wheeler Block-Sorting (Burrows and

Wheeler, 1994), i.e., the XML data is rearranged in

such a way that compression techniques such as gzip

achieve higher compression ratios. This approach is

not applicable to data streams, but allows querying

the compressed data if it is enriched with additional

index information.

The approach in (Zhang, Kacholia, and Özsu,

2004) is another succinct representation of XML. It

does not separate the raw data structure that de-

scribes the document tree from the tokens represent-

ing the elements. Therefore, one byte is required to

represent an end-tag, whereas our approach, BSBC,

only needs one bit. Furthermore, our separation of

structural data from element names does not only al-

low for a better compression as shown in the evalua-

tion; it also enables a more efficient evaluation of

path queries because raw bit data can be compared

more efficiently than tokens. A second difference is

our use of inverted element lists instead of token-

dictionaries, which additionally increases the speed

of path query evaluation significantly because the

number of possible path hits can be reduced quite

fast with a simple lookup within the inverted list.

To the best of our knowledge, the separation of

an XML stream into different compressed streams

linked by a bit stream that is also used to evaluate

path queries is unique to our compression technique,

WEBIST 2008 - International Conference on Web Information Systems and Technologies

and there is no other XML compression system that

combines the advantages of our approach.

6 SUMMARY AND

CONCLUSIONS

We have presented Bit-Stream-Based-Compression

(BSBC), a two-step XML compression approach

that is based on DAG compression and supports the

compression of XML streams and path queries on

compressed data by combining the following advan-

tages. First, both transformation steps can be exe-

cuted in a pipelined fashion, which avoids storing in-

termediate data or streams. Second, an XML data

stream is separated into its constituent parts: the

DAG structure, represented as a bit stream and a

sub-tree pointer stream; the sequence of elements

and attributes, stored in inverted lists together with

their corresponding bit stream positions; and finally,

the constants, stored in different containers depend-

ing on the element or the attribute embedding the

value. This separation allows adapting the compres-

sion technique to the node type, i.e., to compress ele-

ments and attributes different from constants. Third,

the bit stream and the sub-tree pointer stream sup-

port fast navigation along all the forward axes.

Forth, inverted lists not only provide a better com-

pression of elements and attributes, but, in combi-

nation with the bit stream, they also support efficient

path queries. Fifth, constants are grouped together

according to their embedding element or attribute to

achieve better compression.

Our comparative evaluation with other available

XML compression approaches shows that BSBC

achieves a better compression ratio within our ex-

periments than the other approaches that support

path queries, i.e. XGrind and DTD substraction, that

BSBC beats gzip, and that BSBC even sometimes

beats XMill.. BSBC is thus a very useful technique

for applications that require the exchange and query-

ing of large XML data sets or XML streams on plat-

forms with limited bandwidth or energy, as e.g. mo-

bile networks.

REFERENCES

A. Arion, A. Bonifati, I. Manolescu, A. Pugliese. XQueC:

A Query-Conscious Compressed XML Database, to

appear in ACM Transactions on Internet Technology.

R. J. Bayardo, D. Gruhl, V. Josifovski, and J. Myllymaki.,

2004. An evaluation of binary xml encoding optimiza-

tions for fast stream based XML processing. In Proc.

of the 13th international conference on World Wide

Web.

S. Böttcher, R. Steinmetz, N. Klein, 2007. XML Index

Compression by DTD Subtraction. International Con-

ference on Enterprise Information Systems (ICEIS).

S. Böttcher and R. Steinmetz, 2007. Data Management for

Mobile Ajax Web 2.0 Applications. DEXA.

P. Buneman, M. Grohe, Ch. Koch, 2003. Path Queries on

Compressed XML. VLDB.

M. Burrows and D. Wheeler, 1994. A block sorting loss-

less data compression algorithm. Technical Report

124, Digital Equipment Corporation.

G. Busatto, M. Lohrey, and S. Maneth, 2005. Efficient

Memory Representation of XML Dokuments, DBPL.

K. Selçuk Candan, Wang-Pin Hsiung, Songting Chen,

Jun'ichi Tatemura, Divyakant Agrawal, 2006. AFilter:

Adaptable XML Filtering with Prefix-Caching and

Suffix-Clustering. VLDB.

J. Cheney, 2001. Compressing XML with multiplexed hi-

erarchical models. In Proceedings of the 2001 IEEE

Data Compression Conference (DCC 2001).

J. Cheng, W. Ng: XQzip, 2004. Querying Compressed

XML Using Structural Indexing. EDBT.

P. Ferragina, F. Luccio, G. Manzini, and S. Muthukri-

shnan, 2006. Compressing and Searching XML Data

Via Two Zips. In Proceedings of the Fifteenth Inter-

national World Wide Web Conference.

M. Girardot and N. Sundaresan. Millau, 2000. An Encod-

ing Format for Efficient Representation and Exchange

of XML over the Web. Proceedings of the 9th Interna-

tional WWW Conference.

D.A. Huffman, 1952. A method for the construction of

minimum-redundancy codes. In: Proc. of the I.R.E.

H. Liefke and D. Suciu, 2000. XMill: An Efficient Com-

pressor for XML Data, Proc. of ACM SIGMOD.

J. K. Min, M. J. Park, C. W. Chung, 2003. XPRESS: A

Queriable Compression for XML Data. In Proceed-

ings of SIGMOD.

W. Ng, W. Y. Lam, P. T. Wood, M. Levene, 2006: XCQ:

A queriable XML compression system. Knowledge

and Information Systems.

D. Olteanu, H. Meuss, T. Furche, F. Bry, 2002: XPath:

Looking Forward. EDBT Workshops.

A. Schmidt, F. Waas, M. Kersten, M. Carey, I. Manolescu,

and R. Busse, 2002. XMark: A benchmark for XML

data management. Hong Kong, China.

P. M. Tolani and J. R. Hartisa, 2002. XGRIND: A query-

friendly XML compressor. In

Proc. ICDE.

B. B. Yao and M. T. Özsu, 2002. XBench - A family of

benchmarks for XML DBMS.

N. Zhang, V. Kacholia, M. T. Özsu, 2004. A Succinct

Physical Storage Scheme for Efficient Evaluation of

Path Queries in XML. ICDE

BSBC: TOWARDS A SUCCINCT DATA FORMAT FOR XML STREAMS