PAYSTAR: A DENOMINATION FLEXIBLE MICROPAYMENT
SCHEME
Sung-Ming Yen, Hsi-Chung Lin, Yen-Chang Chen
Dept of Computer Science and Information Engineering
National Central University, Chung-Li, Taiwan 320, R.O.C.
Jia-Jun Hung, Jui-Ming Wu
Networks and Multimedia Institute, Institute for Information Industry, Taiwan, R.O.C.
Keywords:
Cryptography, Electronic payment, Micropayment, One-time password, One-way hash chain.
Abstract:
In this paper, a micropayment scheme with flexible coin denomination mintage is proposed. This varying
denomination approach might be more reasonable for most micropayment applications. Furthermore, the
proposed scheme improves extensively the computational performance of both the customer as well as the
merchant. Storage cost of the customer is exactly the same as in the original PayWord micropayment scheme
and is thus applicable to implementations on small portable devices, e.g., smart card.
1 INTRODUCTION
Micropayment schemes have received growing atten-
tion recently, primarily because that these schemes
provide solutions for numerous Internet based appli-
cations. Micropayment schemes allow a customer to
transfer to a merchant a sequence of small amount
payments in exchange for services or electronic prod-
ucts from the merchant. Usually, it is inappropriate
to pay the total amount of money either in advance or
afterwards in some applications, and this makes mi-
cropayment schemes be especially useful. The result
is that efficient and cryptographically strong micro-
payment schemes are highly demanded to provide ac-
ceptable performance and also to solve dispute when
occurred.
For most application scenarios of micropayment,
both the computational cost and the storage cost
should be reduced to maintain acceptable perfor-
mance.
• Computational cost reduction: Since the pay-
ment is small and might be very frequent, this cost
should be reduced. Evidently, the employment of
public key cryptography should be minimized if
possible.
• Storage cost reduction: For most micropayment
applications, huge amount of payment records
might need to take care. Therefore, minimization
on storage cost will be helpful.
Furthermore, administrative cost that includes the
interactions with the trusted third party (usually the
bank) and the frequency of doing withdraw and de-
posit should also be minimized.
Due to the potential applications, many research
results about micropayment schemes design and their
performance enhancement have been published in the
past few years (Glassmann et al., 1995; Rivest and
Shamir, 1997; Jutla and Yung, 1996; Pedersen, 1997;
Stern and Vaudenay, 1998; Yen et al., 1999; Micali
and Rivest, 2002). One large category of micropay-
ment schemes (e.g., the PayWord scheme (Rivest and
Shamir, 1997) by Rivest and Shamir) use one-way
hash chain as the primary cryptographic tool to de-
velop the schemes.
A conventional one-way hash chain is recursively
defined from a secret value by performing a se-
quence of cryptographic hash computations, e.g.,
(SHA-1, 1995). This simple design of linear one-
way hash chain makes the PayWord-like micropay-
ment schemes have their intrinsic disadvantage that
more longer a one-way hash chain will lead to a less
efficient performance of generating a micropayment
coin. Some approaches (Jutla and Yung, 1996; Yen
et al., 1999) had been proposed trying to overcome
the above mentioned disadvantage, however each of
them has its merit and also limitation or even disad-
vantage.
In the conventional PayWord-like schemes and the
modified versions (e.g., (Jutla and Yung, 1996; Yen
387
Yen S., Lin H., Chen Y., Hung J. and Wu J. (2008).
PAYSTAR: A DENOMINATION FLEXIBLE MICROPAYMENT SCHEME.
In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 387-393
DOI: 10.5220/0001521103870393
Copyright
c
 SciTePress

et al., 1999)), each coin is defined to be of the same
smallest denomination, but this brings some perfor-
mance overhead for the merchant and also for the cus-
tomer if each payment will be a random times of the
smallest denomination.
Our Contribution. The main contribution of this
paper is that we propose a new micropayment
scheme, called the PayStar scheme, that employs the
proposed merged one-way hash chain and provides
a flexible design of varying denomination. The re-
sult is that average computational cost of generating
each smallest denomination for the customer is re-
duced extensively when compared with the conven-
tional PayWord scheme and the enhanced tree-based
scheme (Yen et al., 1999).
This performance enhancement is important for
micropayment schemes that will be implemented
based on small portable devices with limited resource,
e.g., smart card. Furthermore, the computational cost
of coin validation performed by the merchant is also
reduced extensively on average for most of the cases,
and the cost is basically independent to the amount to
pay.
2 RELATED WORK
Some notations and symbols used in this paper about
a one-way hash chain are given in the following.
Definition 1 When a function h is iteratively applied
r times to an argument v
n
, the result will be denoted
as h
r
(v
n
), that is
h
r
(v
n
) = h(h(···(h
| {z }
r times
(v
n
))··· )).
When the function h() in the iteration is instan-
tiated with a one-way hash function, such as SHA
(SHA-1, 1995), the result is a one-way hash chain as
shown below
v
0
= h
n
(v
n
) ← v
1
= h
n−1
(v
n
) ← · ··
·· · ← v
n−1
= h
1
(v
n
) ← v
n
.
Note that within the chain, each element v
i
is com-
puted as h
n−i
(v
n
).
2.1 Brief Review of the PayWord
Scheme
PayWord is a credit-based micropayment scheme pro-
posed by Rivest and Shamir (Rivest and Shamir,
1997). Prior to the first transaction taking place be-
tween a customer C and a merchant M, the following
preparatory steps need to be carried out.
(1) The customer generates a payword chain as fol-
lows:
v
0
← v
1
← v
2
← ·· · ← v
n−1
← v
n
where v
i
= h(v
i+1
) for i = n − 1,n − 2, ··· ,1,0,
and h() is a cryptographic one-way hash function.
The value v
n
is a secret value selected at random
by the customer.
(2) The customer signs, e.g., using RSA (Rivest et al.,
1978), on the root v
0
, together with the merchant’s
identity and other information:
Sign
C
(Merchant-ID||v
0
||Cert)
where “Cert” used as a proof of credentials is a
digital certificate issued to the customer by the
bank B. The certificate authorizes the customer to
mint his own payword chains. Note that the sig-
nature on (Merchant-ID||v
0
||Cert) acts as a com-
mitment.
(3) The customer then sends
Sign
C
(Merchant-ID||v
0
||Cert),
Merchant-ID, v
0
,Cert
to the merchant.
After completing successfully the above steps be-
tween the customer and the particular merchant, the
number v
i
(i = 1,2,. .., n) can now be used as the ith
coin to be paid. Each coin v
i
in the sequence is pre-
defined to be of one smallest denomination. When re-
ceiving a new coin v
i
from the customer, the merchant
verifies whether v
i−1
?
= h(v
i
). The merchant accepts v
i
as a valid payment only if the verification is success-
ful. Note that the merchant can store a validv
i
in place
of v
i−1
. The above process ensures that a sequence of
small payments can be paid to a specific merchant and
the customer has to perform only one computationally
expensive public key based digital signature which is
for the purpose of commitment.
Suppose v
x
is the previously spent coin and the
customer now needs to spend t times of the smallest
denomination, then the customer computes and sends
v
i
= v
x+t
to the merchant. When receiving v
i
from the
customer, the merchant verifies whether v
x
?
= h
t
(v
i
).
2.2 Micropayment based on
Unbalanced One-way Binary Tree
At the customer’s side, suppose that he only stores the
last coin v
n
, then he has to compute each required new
coin by a sequence of hash function computations. It
is evident that on average each new coin generation
WEBIST 2008 - International Conference on Web Information Systems and Technologies
388

will cost ((n − 1) + (n− 2) + ··· + 1)/n = (n − 1)/2
(or roughly n/2 for large n) hash computations.
In (Yen et al., 1999), the technique of one-way
hash chain was extended into a multi-dimensional
tree-based approach which is called the unbalanced
one-way binary tree (UOBT). An unbalanced one-
way binary tree is essentially a bundle of many one-
way hash chains, with their secret values (called the
seed nodes in PayWord scheme) being tied together
via another separate one-way hash chain.
In the unbalanced one-way binary tree with n
nodes (coins), given the seed value v
n
, each v
i
can
be computed using on average
O
(n
1/2
) hash compu-
tations (Yen et al., 1999). Therefore, the usage of un-
balanced one-way binary tree brings extensive perfor-
mance improvement over the conventional linear one-
way hash chain.
3 THE PROPOSED
DENOMINATION FLEXIBLE
MICROPAYMENT SCHEME
In most applications, each payment request for dif-
ferent purchase might differ from each other. Sup-
pose that each payment is a random amount between
one time to 2
k+1
times of the smallest denomina-
tion (say one cent), and the expected average pay-
ment is roughly 2
k
cents. In the conventional one-
way hash chain and the unbalanced one-way binary
tree designs, each coin v
i
is defined to represent the
smallest denomination. In such fixed denomination
approaches, the merchant needs to perform 2
k
hash
computations to validate the correctness of a payment
with 2
k
cents.
In this section, a new micropayment scheme with
variable denomination is proposed in which the com-
putational cost of payment validation performed by
the merchant is reduced for the average case. Ba-
sically, the computational cost is independent to the
amount being paid.
3.1 Varying Denomination Mintage
Scheme
Each payment will be assigned a denomination be-
tween [1, 2
k+1
]. Suppose the denomination of the
ith payment is D cents and D− 1 be binary encoded
as (d
k
,· ·· ,d
1
,d
0
)
2
. For this payment of D cents, a
merged one-way hash chain will be defined in the fol-
lowing
c
i,k
= h(c
i,k−1
kh(x
i,k
))
← c
i,k−1
=h(c
i,k−2
kh(x
i,k−1
))
← ·· · ← c
i,0
=h(ckh(x
i,0
)) ← c
where x
i, j
(j = k,k− 1,··· ,0) are secret values and c
is a public information. To pay D cents, the sequence
of values below (called the trapdoor sequence) will
be released to the merchant
(h
1−d
k
(x
i,k
),··· ,h
1−d
1
(x
i,1
),h
1−d
0
(x
i,0
))
where h
0
(x
i, j
) = x
i, j
.
The basic idea is to encode the denomination D (a
positiveinteger) into a merged one-wayhash chain. In
the trapdoor sequence, h
1−d
k
(x
i,k
) and h
1−d
0
(x
i,0
) will
be used to encode the most significant bit d
k
and the
least significant bit d
0
of D− 1, respectively. If d
j
= 1
then the secret x
i, j
will be released to the merchant,
otherwise h(x
i, j
) will be released. So, given c, c
i,k
,
and the corresponding trapdoor sequence, a unique
denomination D can be specified by the merged one-
way hash chain.
For example, let k = 2, the denomination of six
cents can be minted by releasing (x
i,2
,h(x
i,1
),x
i,0
).
3.2 PayStar Scheme with Varying
Denomination
Let the payment of each purchase be a random
amount between one cent to 2
k+1
cents with the ex-
pected average payment of (2
k
+
1
2
) cents, and we
wish to prepare a payment token of totally n cents
on average. The proposed PayStar scheme with ℓ =
n/(2
k
+
1
2
) merged one-way hash chains is shown be-
low.
(1) The customer prepares ℓ = n/(2
k
+
1
2
) indepen-
dent merged one-way hash chains all with the
same public information c and each being capable
of encoding denomination between [1,2
k+1
]. All
the last values c
i,k
(i = 1,2,·· · ,ℓ) of all the cor-
responding merged one-way hash chains are com-
puted. Fig. 1 illustrates the construction.
All the secret values x
i, j
of the merged one-way
hash chains can be defined as x
i, j
= h(x,i, j) or
alternatively by using conventional block cipher
x
i, j
= E
x
(i, j) where x is a secret value selected at
random by the customer. So, the customer only
needs to store a secret value, i.e., x.
(2) The customer signs on the merchant’s identity, the
public information c (which can be any constant),
the roots (c
1,k
,· ·· ,c
ℓ,k
) of all the merged one-way
PAYSTAR: A DENOMINATION FLEXIBLE MICROPAYMENT SCHEME
389

c
↓
↓↓
↓
c
1,0
↓
↓↓
↓
c
1,1
↓
↓↓
↓
…
↓
↓↓
↓
c
1,k
c
↓
↓ ↓
↓
c
i
,
0
↓
↓ ↓
↓
c
i
,
1
↓
↓ ↓
↓
↓
↓ ↓
↓
c
i
,
k
…
c
↓
↓ ↓
↓
c
l
,
0
↓
↓ ↓
↓
c
l
,
1
↓
↓ ↓
↓
↓
↓ ↓
↓
c
l
,
k
…
c
↓
↓ ↓
↓
c
2
,
0
↓
↓ ↓
↓
c
2
,
1
↓
↓ ↓
↓
…
↓
↓ ↓
↓
c
2
,
k
c
↓
↓ ↓
↓
c
j
,
0
↓
↓ ↓
↓
c
j ,
1
↓
↓ ↓
↓
↓
↓ ↓
↓
c
j
,k
…
c
↓
↓ ↓
↓
c
3
,
0
↓
↓ ↓
↓
c
3
,
1
↓
↓ ↓
↓
…
↓
↓ ↓
↓
c
3
,
k
… …
… …
… …
Figure 1: PayStar scheme with varying denomination.
hash chains, an integer parameter k, and the cer-
tificate issued by the bank
Sign
C
(Merchant-IDkck(c
1,k
,· ·· ,c
ℓ,k
)kkkCert)
where k is used to indicate that the denomina-
tion of payment is between [1, 2
k+1
] cents. The
above signature (used as the payment commit-
ment), Merchant-ID, c, (c
1,k
,· ·· ,c
ℓ,k
), k, and Cert
will be sent to the merchant before the first pur-
chase.
The merchant validates the correctness of the pay-
ment commitment and stores the commitment as
well as the following values for further transaction
verification
{c,(c
1,k
,· ·· ,c
ℓ,k
),k}.
(3a) To pay D cents to the merchant as the ith payment,
the customer prepares the corresponding trapdoor
sequence S
(s
k
,· ·· ,s
1
,s
0
)
= (h
1−d
k
(x
i,k
),··· ,h
1−d
1
(x
i,1
),h
1−d
0
(x
i,0
))
of the denomination D where (d
k
,· ·· ,d
1
,d
0
)
2
is
the binary representation of D− 1.
(3b) After receiving the trapdoor sequence S , the mer-
chant verifies the validity of S by computing
c
i,k
?
= h(·· ·h(h(ckh
d
0
(s
0
))kh
d
1
(s
1
))··· kh
d
k
(s
k
))
based on the definition of the merged one-way
hash chain and the stored root c
i,k
. Correct vali-
dation of S confirms the committed denomination
D. In fact, after verifying and storing the trapdoor
sequence S , the root c
i,k
is no longer necessary.
Therefore, a PayStar token is essentially a bundle
of many merged one-way hash chains, with their pub-
lic information c being tied together by selecting a
common value.
To avoid the merchant searching among all the
previously received payment from a specific PayStar
token to detect any possible double spending, the root
c
i,k
of each merged one-way hash chain can be re-
defined as c
i,k
=h(ikc
i,k−1
kh(x
i,k
)).
3.3 Security Analysis of the PayStar
Scheme
In the PayStar scheme, it is impossible for a dishon-
est customer to double spend, as long as the mer-
chant ensures that each merged one-way hash chain
of a PayStar token can only be used once. In prac-
tice, since the customer is forced to spend his merged
one-way hash chains in sequence and the merchant
promptly deletes the root c
i,k
after the i-th payment
is validated, the PayStar scheme is evidently double
spending free.
Similarly, it is impossible for a dishonest merchant
to double encash at the redemption, as long as the
bank ensures that each payment corresponds to a dif-
ferent merged one-way hash chain. It is also impossi-
ble for a dishonest merchant to over encash at the re-
demption since enlarging the denomination of a used
merged one-way hash chain requires the ability of ex-
tracting pre-images of some (at least one) items in
the trapdoor sequence. Clearly, the merchant’s abil-
ity of extracting pre-images contradict the one-way
property of the underlying hash function.
4 PERFORMANCE ANALYSIS
4.1 Computational and Storage Cost
Analysis
We assume that the probability of appearance of de-
nomination D (1 ≤ D ≤ 2
k+1
) for each payment is
the same. So, the expected amount of money (in
cent) that will be embedded in a PayStar token with ℓ
merged one way hash chains is
E = (1+ 2
k+1
)ℓ/2
(roughly ℓ×2
k
for large k). The customer takes on av-
erage 1.5× (k+ 1) hash computations to obtain each
necessary trapdoor sequence. Therefore, to spend
the whole PayStar token, the customer needs totally
1.5× ℓ× (k+ 1) hash computations, and the spending
of each “cent” costs on average
(1.5× ℓ × (k+ 1))/E ≈ (1.5× (k + 1))/2
k
hash computations. Here, we ignore the computa-
tional cost to prepare the PayStar token since this can
WEBIST 2008 - International Conference on Web Information Systems and Technologies
390

be off-line performed. Totally, 3 × ℓ × (k + 1) hash
computations are necessary to prepare the PayStar to-
ken.
Like in the original PayWord scheme and the
UOBT-based micropayment scheme, the customer
needs only to store the secret value x.
For the merchant, after receiving the trapdoor se-
quence representing a committed denomination D,
the related merged one-way hash chain will be em-
ployed to validate the denomination with on aver-
age 1.5 × (k + 1) hash computations. Therefore, for
the whole PayStar token, the merchant needs totally
1.5× ℓ × (k+ 1) hash computations, and the verifica-
tion of each “cent” costs on average
(1.5× ℓ × (k+ 1))/E ≈ (1.5× (k + 1))/2
k
hash computations which is exactly the same cost of
spending each cent by the customer.
Knowledge of the trapdoor sequence (with k + 1
hash values) is sufficient for the committed denom-
ination D, so now the merchant can remove the re-
lated root c
i,k
. If the whole PayStar token is spent,
the merchant needs to store ℓ trapdoor sequences, i.e.,
ℓ × (k + 1) hash values, for all of the committed de-
nominations.
Suppose that ℓ = 100, k = 5, and the bit length of
each hash value is 160, then the expected total amount
of money embedded in the PayStar token is E = 3250
cents and it costs the merchant about 12 kilobytes to
store all of the 100 trapdoor sequences. In this exam-
ple, the amount of money embedded in the PayStar to-
ken is quite sufficient for micropayment applications
and the storage cost remains acceptable and practical.
4.2 Alternative Merged One-way Hash
Chain
An alternative (generalized) merged one-way hash
chain is possible which can be used to improve the
performance of both the customer and the merchant.
Furthermore, this generalized merged one-way hash
chain will reduce the storage cost of the merchant.
To assign a denomination D, let D − 1 be repre-
sented with radix r as (d
k
,· ·· ,d
1
,d
0
)
r
where 0≤ d
i
≤
r − 1. With this design, the denomination can be in
the range 1 ≤ D ≤ r
k+1
. Now, a merged one-way hash
chain will be defined as
c
i,k
= h(c
i,k−1
kh
r−1
(x
i,k
))
← c
i,k−1
=h(c
i,k−2
kh
r−1
(x
i,k−1
))
← ·· · ← c
i,0
=h(ckh
r−1
(x
i,0
)) ← c
and the trapdoor sequence to be released to the mer-
chant becomes
(h
r−1−d
k
(x
i,k
),··· , h
r−1−d
1
(x
i,1
),h
r−1−d
0
(x
i,0
)).
In the trapdoor sequence, h
r−1−d
k
(x
i,k
) and
h
r−1−d
0
(x
i,0
) will be used to encode the most sig-
nificant digit d
k
and the least significant digit d
0
of
D− 1, respectively. Following the same reasoning in
Sect. 4.1, it is clear that the average cost for the cus-
tomer to spend and for the merchant to validate one
cent are both
(
r+ 1
2
× ℓ × (k + 1))/E = (r+ 1)(k+ 1)/(1+ r
k+1
)
hash computations, where E = (1+ r
k+1
)ℓ/2. As for
the storage cost, the customer needs only to store one
secret value and the merchant need to store ℓ trapdoor
sequences, i.e., ℓ × (k + 1) hash values.
Theorem 1 Let each x
i, j
be computed by x
i, j
=
h(x,i, j) with one hash computation. Then, the com-
putationally optimal design of merged one-way hash
chain for any predetermined maximum possible de-
nomination is to select r = 4.
Proof: Let D be the predetermined maximum pos-
sible denomination to be encoded, r the radix, k + 1
the length of the merged one-way hash chain, then
r
k+1
= D . The average number of hash computa-
tions that the customer needs to prepare the trapdoor
sequence is (k + 1) × (r + 1)/2, and this is also the
same amount of computation that the merchant needs
to verify the trapdoor sequence. For a specific radix
r, k+ 1 = log
r
D , so the computational cost becomes
(k+ 1) ×
r+1
2
=
r+1
lnr
×
lnD
2
.
For anypredetermined maximum possible denom-
ination D , to minimize the computational cost is to
minimize
r+1
lnr
and m(r) =
d(
r+1
lnr
)
dr
=
1
lnr
−
r+1
(lnr)
2
r
. We
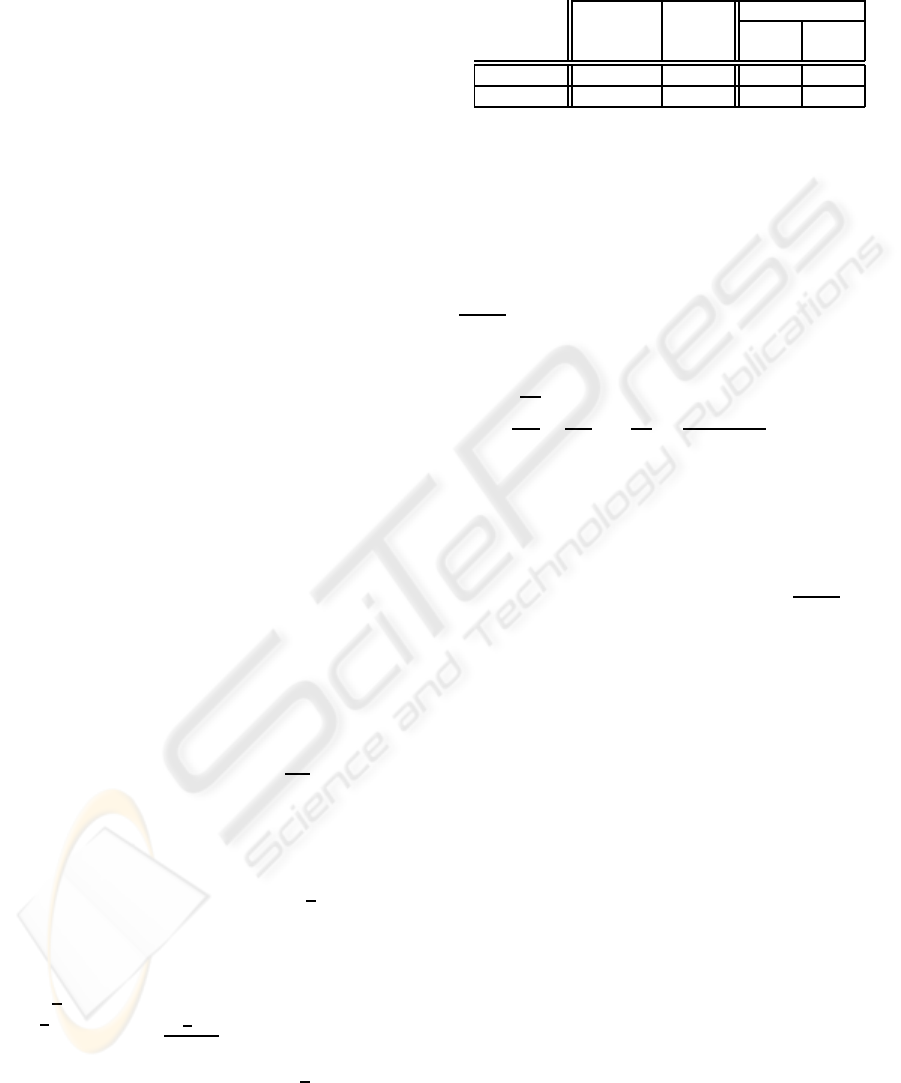
have m(3.59114) = 0 when r ≥ 2, and the mini-
mum value of
r+1
lnr
(for r ∈ IN and r ≥ 2) becomes
4+1
ln4
= 3.6067375 (see Fig. 2).
The result is that r = 4 for any D is the best selec-
tion in the proposed merged one-way hash chain. ⊓⊔
The result obtained in Theorem 1 shows that the
implementation of the optimized merged one-way
hash chain can be very easy since a representation
with radix of four can be obtained easily from a repre-
sentation with radix of two. With the same example of
Figure 2: The best selection of radix r.
PAYSTAR: A DENOMINATION FLEXIBLE MICROPAYMENT SCHEME
391

ℓ = 100 and 1 ≤ D ≤ 64 (E = 3250) mentioned previ-
ously, the length of each merged one-way hash chain
will be reduced to 3 (k = 2) when the radix r = 4 is
selected. Therefore, the storage cost of the merchant
will be substantially reduced to about 6 kilobytes (i.e.,
50% reduction) and the computational cost will be re-
duced to 83% for both of the customer and the mer-
chant.
In some cases where the denomination D is de-
signed to be in the range [1 ≤ D ≤ r
k+1
− δ] (where
δ is a large positive integer and δ < r
k
), to assign a
denomination D into the merged one-way hash chain,
radix r representation of (D−1+δ) instead of (D−1)
can be used to compute the trapdoor sequence. In
this modified version, the most significant digit d
k
will now usually have a larger value and h
r−1−d
k
(x
i,k
)
will take fewerhash computations. On the other hand,
the merchant will take more hash computations (when
compared with the customer) to verify the received
trapdoor sequence since he needs more hash compu-
tations to obtain c
i,k
. This design is of course reason-
able because the customer might have only a resource
limited portable device, e.g., smart card, but the mer-
chant can be equipped witha powerful computer. This
modified design becomes especially important due to
the result obtained in Theorem 1 that the optimal radix
r is four but not two, so δ might be a large value.
4.3 Comparisons with other Schemes
In this section, comparisons of performance among
the PayWord scheme (Rivest and Shamir, 1997), the
UOBT scheme (Yen et al., 1999), and the proposed
PayStar will be given. It is assumed that the smallest
denomination is one cent and the cost of each pay-
ment is uniformly distributed over the range of [1,t].
On average, each payment costs A =
1+t
2
cents.
Lemma 1 Let n be the length of a conventional one-
way hash chain and each payment costs A cents on
average. Then, in the PayWord scheme, the expected
computational costs for the customer to spend and for
the merchant to validate each cent are (
n
A
− 1)/2 and
one hash computations, respectively.
Proof: The expected total number of hash com-
putations required to be done by the customer dur-
ing the
n
A
payment transactions (an average case) is
T =
∑
n
A
i=1
(i− 1) · A =
n·(
n
A
−1)
2
.
Therefore, the expected computational cost for the
customer to spend each cent is T/n = (
n
A
− 1)/2 hash
computations. Apparently, the computational cost for
the merchant to validate each cent is one hash compu-
tation. ⊓⊔
Table 1: Comparison of computational cost per cent among
PayWord, UOBT, and PayStar.
PayStar
PayWord UOBT r = 2 r = 4
k = 5 k = 2
Customer 49.5 1.72 0.28 0.23
Merchant 1 1 0.28 0.23
Lemma 2 Suppose that there are p· q nodes (coins)
in an Unbalanced One-way Binary Tree (i.e., q one-
way hash chains each of length p, with their seeds tied
together via another one-way hash chain of length q)
and each payment costs A cents on average. Then,
the expected computational costs for the customer to
spend and for the merchant to validate each cent are
p+q−2
2A
and one hash computations, respectively.
Proof: The expected total number of hash com-
putations required to be done by the customer dur-
ing the
p·q
A
payment transactions (an average case) is
T =

p−1
2
+
q−1
2

×
p·q
A
=
p·q·(p+q−2)
2A
. In this anal-
ysis, for the sake of simplicity, we do not explicitly
consider the case in which a payment may need to
deliver two hash values from two adjacent one-way
hash chains. However, the above brief estimation re-
flects the usual cases in a UOBT setting.
Therefore, the expected computational cost for the
customer to spend each cent is T/(p·q) =
p+q−2
2A
hash
computations. Apparently, the computational cost for
the merchant to validate each cent is one hash compu-
tation. ⊓⊔
Following the example used in Sect. 4.1, a con-
crete comparison can be made by letting the cost of
each payment be a random value in the range [1, 64]
with the average cost A = 32.5, and the expected to-
tal amount embedded in a payment token be about
3250 cents. So, each payment token can be used
for approximately 100 payment transactions before
being exhausted. Parameters corresponding to the
above scenario are n = 3250 for the PayWord scheme,
p = q = 57 (p×q= 3249) for the UOBT scheme, and
ℓ = 100 for the proposed PayStar. Performance com-
parisons of the expected computational cost (number
of hash computations per cent) among these four pay-
ment schemes with the above setting are summarized
in the Table 1.
Table 1 shows that for the computational perfor-
mance of the customer, the proposed PayStar scheme
is substantially superior to all other schemes; and for
the computational performance of the merchant, the
proposed PayStar scheme is also superior to the Pay-
Word scheme and the UOBT scheme.
WEBIST 2008 - International Conference on Web Information Systems and Technologies
392

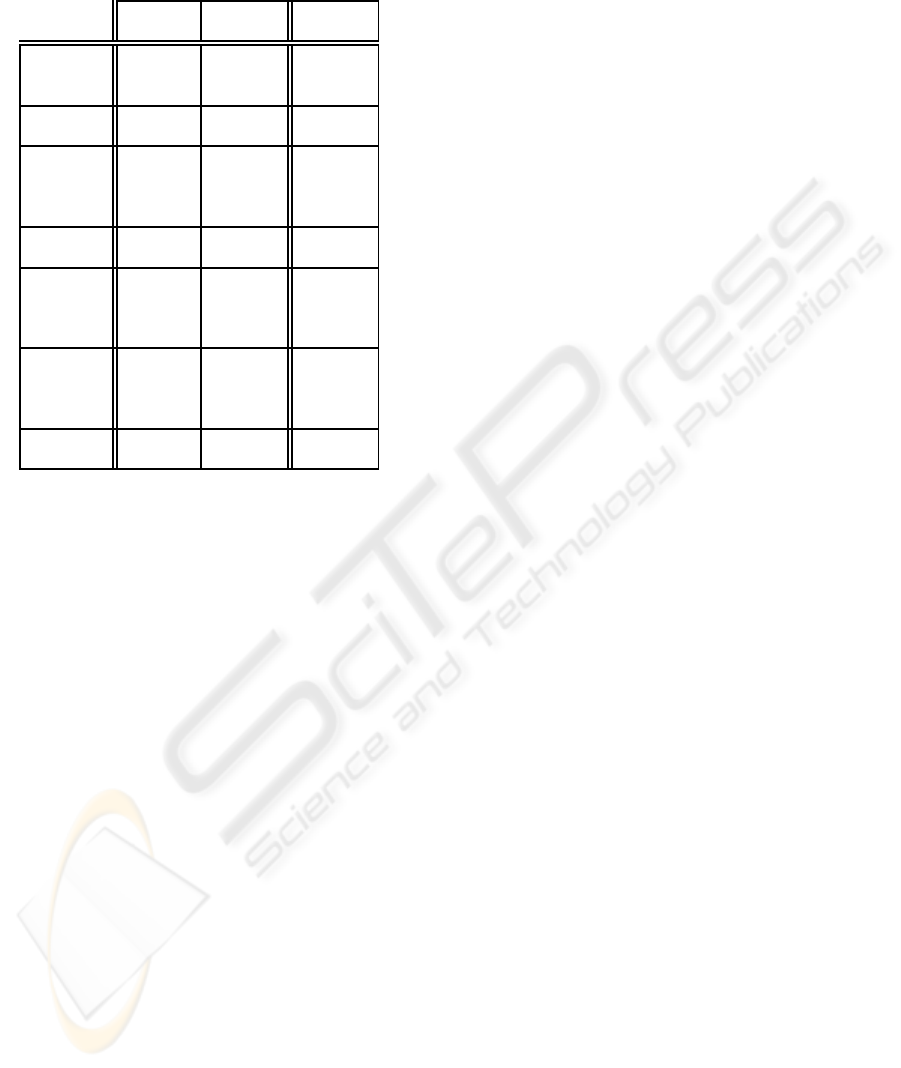
Table 2: Overall comparisons among PayWord, UOBT, and
PayStar.
PayWord UOBT PayStar
unbalanced merged
Building one-way
one-way one-way
block hash chain
binary tree hash chain
Denomi-
nation
fixed fixed flexible
Customer
computation very
cost
inefficient efficient
efficient
(per cent)
Customer
storage cost
very small very small very small
Merchant
computation very
cost
efficient efficient
efficient
(per cent)
Merchant
validation
depend on depend on independent
cost (each
total total to total
transaction)
amount amount amount
Merchant
storage cost
very small very small reasonable
4.4 Further Extension of the PayStar
Scheme
One further extension of the PayStar scheme is pos-
sible by collecting a few groups of merged one-
way hash chains together and each group with their
own predetermined maximum possible denomination.
This design is especially useful when the cost of each
payment might be diverse with large values.
On the other hand, if the PayStar token consists
of a few groups of merged one-way hash chains and
each group with their own predetermined merchant
identity, then a micropayment scheme for multiple
merchants can be readily constructed. One possible
approach of encoding the merchant’s identity into the
merged one-way hash chain is shown below
c
i,k
=h(Merchant-IDkc
i,k−1
kh(x
i,k
)).
5 CONCLUSIONS
The proposed PayStar micropayment scheme with
varying denomination by employing the merged one-
way hash chain performs substantially superior to
both the original PayWord scheme and also the
UOBT-based scheme. Computational performances
of both the customer as well as the merchant have
been enhanced. In the PayStar scheme, storage cost of
the customer is very small which enables the imple-
mentation of the scheme on small portable devices.
Although the merchant suffers from the penalty of
more storage cost, but the overhead is in fact ac-
ceptable according to our analysis on reasonable ex-
amples. Overall comparisons among the PayWord
scheme, the UOBT-based scheme, and the proposed
PayStar scheme are summarized in the Table 2.
ACKNOWLEDGEMENTS
This work was supported in part by Institute for Infor-
mation Industry, R.O.C.
REFERENCES
Glassmann, S., Manasse, M., Abadi, M., Gauthier, P., and
Sobalvarro, P. (1995). The millicent protocol for inex-
pensive electronic commerce. In Proc. of 4th Interna-
tional World Wide Web Conference, pages 603–618.
Jutla, C. and Yung, M. (1996). Paytree: Amortized-
signature for flexible micropayments. In Proc. of 2nd
USENIX Workshop on Electronic Commerce, pages
213–221.
Micali, S. and Rivest, R. (2002). Micropayments revisited.
In Proc. of Cryptographer’s Track at the RSA Confer-
ence, CT-RSA ’02, volume Lecture Notes in Computer
Science 2271, pages 149–163. Springer-Verlag.
Pedersen, T. (1997). Electronic payments of small amounts.
In Proc. of Security Protocols Workshop, volume Lec-
ture Notes in Computer Science 1189, pages 59–68,.
Springer-Verlag.
Rivest, R. and Shamir, A. (1997). Payword and micromint:
Two simple micropayment schemes. In Proc. of
Security Protocols Workshop, volume Lecture Notes
in Computer Science 1189, pages 69–87. Springer-
Verlag. Also in CryptoBytes, Pressed by RSA Lab-
oratories, Vol. 2, No. 1, pp. 7–11, 1996.
Rivest, R., Shamir, A., and Adleman, L. (1978). A method
for obtaining digital signatures and public-key cryp-
tosystem. Commun. of ACM, 21(2):120–126.
SHA-1 (1995). FIPS 180-1, secure hash standard. Technical
report, NIST, US Department of Commerce, Washing-
ton D.C.
Stern, J. and Vaudenay, S. (1998). Svp: A flexible micro-
payment scheme. In Proc. of Financial Cryptography
Conference, FC ’97, volume Lecture Notes in Com-
puter Science 1318, pages 161–172. Springer-Verlag.
Yen, S., Ho, L., and Huang, C. (1999). Internet micro-
payment based on unbalanced one-way binary tree.
In Proc. of International Workshop on Cryptographic
Techniques and E-Commerce, CrypTEC ’99, pages
155–162.
PAYSTAR: A DENOMINATION FLEXIBLE MICROPAYMENT SCHEME
393