EVALUATION OF K-/LATTICE-CLUSTERING ALGORITHMS FOR

RANDOM WIRELESS MULTI-HOP NETWORKS

Toshihiko Sasama, Ryo Monde and Hiroshi Masuyama

Department of Information and Knowledge Engineering, Tottori University, Koyama town, Tottori prefecture, Japan

Keywords:

Ad hoc networks, Broadcast, Clustering, Energy consumption, Protocol, Simulation, Wireless.

Abstract:

A k-clustering protocol is an algorithm in which the wireless network is divided into non-overlapping sub

networks, referred to as clusters, and where every node of a sub network is at most k hops from a distinguished

station called the cluster-head. A lattice-clustering protocol is an algorithm in which a given area is divided by

lattices and randomly distributed hosts in a lattice are one hop from the cluster-head. In this paper, we evaluated

the energy eﬁciencies for the broadcasts designed in both k-clustering and lattice-clustering protocols. The

evaluation showed that the k-clustering protocol is characterized by the smallest broadcasting power of each

node, and a lattice-clustering protocol constitutes a characteristic feature of the most minimal total energy

consumption. The main source of greater energy consumption in k-clustering protocol is a large number of

transmissions between adjacent node pairs.

1 INTRODUCTION

Ad hoc networks consist of wireless hosts that com-

municate without the need of any ﬁxed infrastructure.

These Ad hoc networks are well suited to speciﬁc

and often extreme situations, such as disaster-relief,

law-enforcement, and ﬁre-detection where each host

works as a sensor node, or simply for collaborative

computation in some short-term public events. A k-

clustering protocol is an algorithm in which the wire-

less network is divided into non-overlapping sub net-

works, referred to as clusters, and where every node

of a sub network is at most k hops from a distin-

guished station called the cluster-head. A lattice-

clustering protocol is an algorithm in which a given

area is divided by lattices and randomly distributed

hosts in a lattice are one hop from the cluster-head.

Clustering is commonly used in ad hoc networks in

order to limit the amounts of both energy consumed

for communication and information stored for rout-

ing at individual nodes. The clustering approach is

used to offer scalability and is efﬁcient in a dense net-

work. Several clustering algorithms have been pro-

posed for each different advantage. The basic idea of

(Wu and Dai, 2004) is to reduce the network density

through clustering using a short transmission range.

Then neighboring cluster heads which are 2 or 3 hops

away are connected using a long transmission range,

that is, without using any gateway selection process.

K-clustering, one of the main clustering protocol, re-

quires no special broadcasting power by heads, thus,

a surface can be clustered by nodes with a uniform

power. This advantage means that each node re-

quires and consumes a lesser amount of energy than

that of the 2-level clustering and the 1-level ﬂat ap-

proach. Since, in broadcasting, all nodes are em-

ployed in receiving a message, it is important to dis-

cuss total energy consumption. We assume the sit-

uation that a node broadcasts to all other randomly

distributed (n-1) nodes which can use synchronous ra-

dio transmissions in each of their transmitting ranges.

In this situation, we evaluate the energy efﬁciencies

for the broadcasts designed in both k-clustering and

lattice-clustering. The remainder of this paper is or-

ganized as follows: In Section 2, we introduced the k-

clustering algorithm. The lattice-clustering algorithm

is introduced in Section 3. Section 4 shows our sim-

ulation experiences and results. Finally, our conclu-

sions are expressed in Section 5.

236

Sasama T., Monde R. and Masuyama H. (2008).

EVALUATION OF K-/LATTICE-CLUSTERING ALGORITHMS FOR RANDOM WIRELESS MULTI-HOP NETWORKS.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 236-239

DOI: 10.5220/0001521302360239

 SciTePress

2 K-CLUSTERING ALGORITM

2.1 Algorithm

A k-clustering protocol is an algorithm in which ev-

ery node locates at most k hops from its belonging

cluster-head. Each node knows its own position and

its ID (or IP address), but it is assumed that each node

has no topological information. The transmission ra-

dius of every node is set to the same. Then, for a given

number n of nodes deploying randomly and uniformly

on a surface of size s, there exist the optical values of

both this transmission radius r and the clustering value

k which lead to the condition where everynode knows

cluster in which its belongs and every gate way knows

the list of its adjacent clusters. Gate way is a node

whose communication range contains nodes belong-

ing to other clusters. This study has been performed

by (Ravelomanana, 2005), he gave the theorem that,

for any ﬁxed constant l , there exists a constant C(l)

such that if r is set to

r =

(1+ l)|S|logn

πn

(1)

every node may have received all the identities of

each of its neighbors. In this paper, we use the above

r when l is 0, and the same k as in (Ravelomanana,

2005).k=an integer log(log n) discarded under the

decimal point.

[Algorithm]

1. Find a node with the smallest ID. Label a cluster

head to the node.

2. Let every node, located at most k hops from the

newest cluster head but not yet a member of other

clusters, be a member belonging to the newest

cluster head. Remove IDs from the cluster head

and the member nodes.

3. Repeat processes 1 and 2 until every node belongs

to a cluster.

4. Label a gateway to the node if a node belonging to

another cluster locates in the transmission radius

of the node.

An example of k=2: Fig. 1 shows an example of 2-

clustering where node ci (i=1-7) mean cluster heads.

2.2 Broadcasting in K-clustering

The procedure of broadcasting is as follows:

1. A source node broadcasts its information in its

transmitting range.

2. Each node which received the information broad-

casts it in the transmitting range.

Figure 1: A K=2 clustering where 2 dotted lines ... and

... mean 1 hop and 2 hops regions from each cluster head,

respectively.

Figure 2: An example of broadcasting in 2-clustering.

3. A cluster head which has received a source node’s

information broadcasts it to every one of its mem-

bers at most 2 steps.

4. A source node (gate way) which received the

information from a node (gate way) located in the

adjacent cluster broadcasts the information within

its transmitting range just like a source node in its

cluster.

Fig. 2 shows an example of broadcasting in 2-

clustering.

3 LATTICE-CLUSTERING

ALGORITHM

3.1 Algorithm

A lattice-clustering protocol is an algorithm in which

a given domain is divided by NN lattices as shown in

Fig.3 and randomly distributed hosts in a lattice are

one hop from the cluster-head. This lattice-clustering

protocol is divided into 2 kinds: one is where the

transmitting range of each cluster-head reaches all

8 adjacent cluster-heads and the other includes only

4 of the closest cluster-heads. They are labeled as

Lattice (8) and Lattice (4) in the following section.

[Algorithm]

1. Find the closest node to the center of each lattice-

cluster.

2. Label a cluster head to the node.

EVALUATION OF K-/LATTICE-CLUSTERING ALGORITHMS FOR RANDOM WIRELESS MULTI-HOP

NETWORKS

237

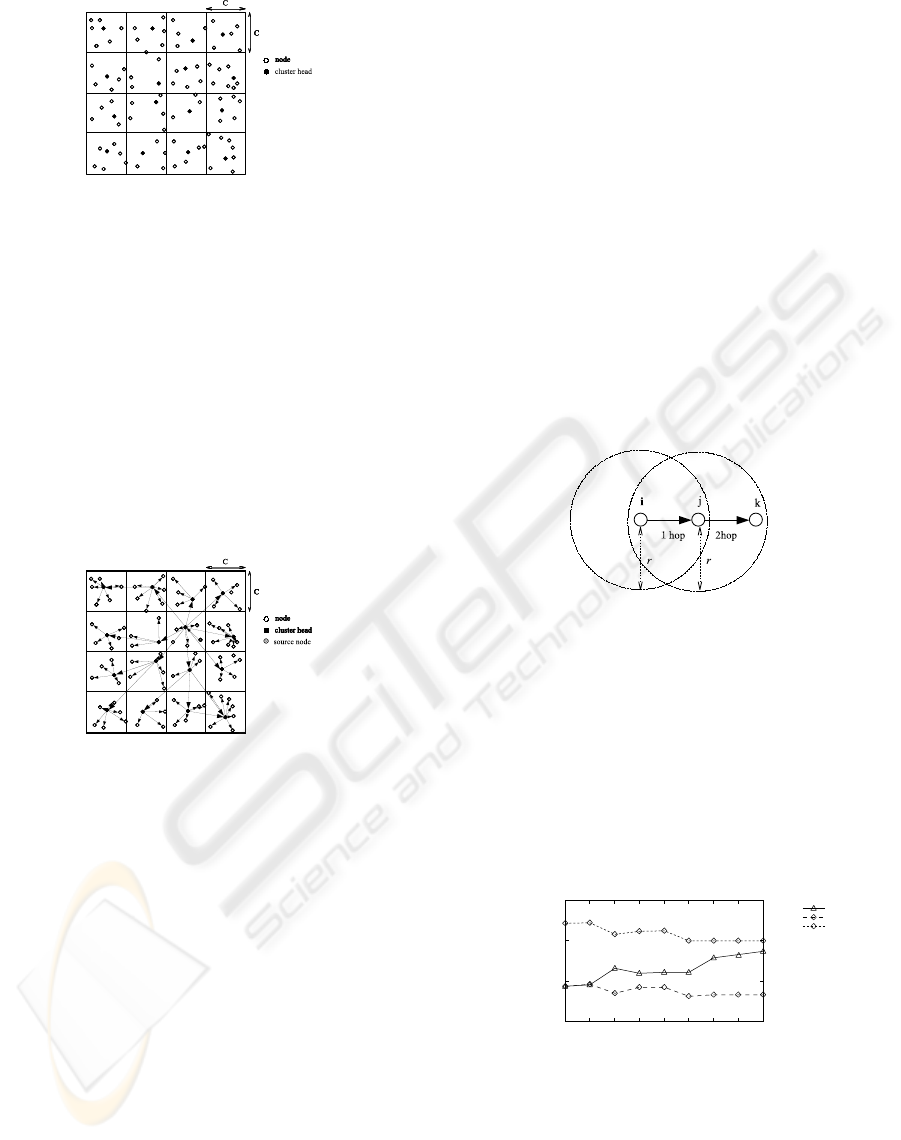
Figure 3: A lattice-clustering of 4 X 4.

3.2 Broadcasting in Lattice-clustering

The procedure of broadcasting is as follows:

1. A source node broadcasts its information in its

transmitting range.

2. A cluster head which received source node’s

information from the adjacent cluster head broad-

casts it to every one of its members in its own

lattice-cluster.

Fig. 4 shows an example of broadcasting in a 4 X 4

lattice-clustering.

Figure 4: Example of broadcasting in a 4 X 4 lattice-

clustering.

4 SIMULATION EXPERIENCES

AND RESULTS

We adopt a commonly encountered model of a net-

work where n homogeneous nodes are randomly

thrown in a given region S, uniformly and indepen-

dently, (Wieselthier, 2000). As is customary, the time

is assumed to be slotted and in each time slot every

node can act either as a transmitter or as a receiver,

but not both. In any given time slot, if and only if a

node acting as a receiver gets a message, exactly one

of its neighbors precisely transmits within the same

round. If more than two neighbors of a node trans-

mit simultaneously, the node is assumed to receive no

message. The neighbors of a node are not permanent

within a number of slots, because of unstable network

topology.

4.1 Simulation Experience

This section describes the input parameters and output

measures for the evaluation of the volume of energy

consumption in 2 kinds of clustering. For simula-

tion purposes, we consider a 100x100 square domain

where 100, 200,

...

, 800 and 900 nodes are randomly

distributed. In k-clustering, we set the values of clus-

tering k and the transmitting range as the values given

in (Ravelomanana, 2005) as mentioned in Section 1.

In lattice-clustering, we set a domain divided by 3x3,

4x4 ,

...

, 15x15, and 16x16. We evaluate the volume of

energy consumption for the broadcasting in transmit-

ting range r as r2 (Wieselthier, 2000). Therefore, the

broadcasting power Pik required from i to k as shown

in (2) and Fig. 5.

Pik = Pij + Pjk = r

+ r

= 2r

(2)

Figure 5: Broadcasting power required from i to k via j.

4.2 Results 1

Fig. 6 depicts the volumes of energy consumptions

required in a broadcast for the total number of nodes.

Fig. 7 depicts the broadcasting power required in each

cluster head for the number of nodes. As shown in

Fig. 6, Lattice (4) is best among three clustering algo-

rithms. Fig. 7 shows that k(=2)-clustering saves the

broadcasting power to cluster heads the most.

30000

50000

70000

90000

100 200 300 400 500 600 700 800 900

Energy counsumption

Number of node

mesh(4)

mesh(8)

Figure 6: Volumes of energy consumption required in a

broadcast.

4.3 Results 2

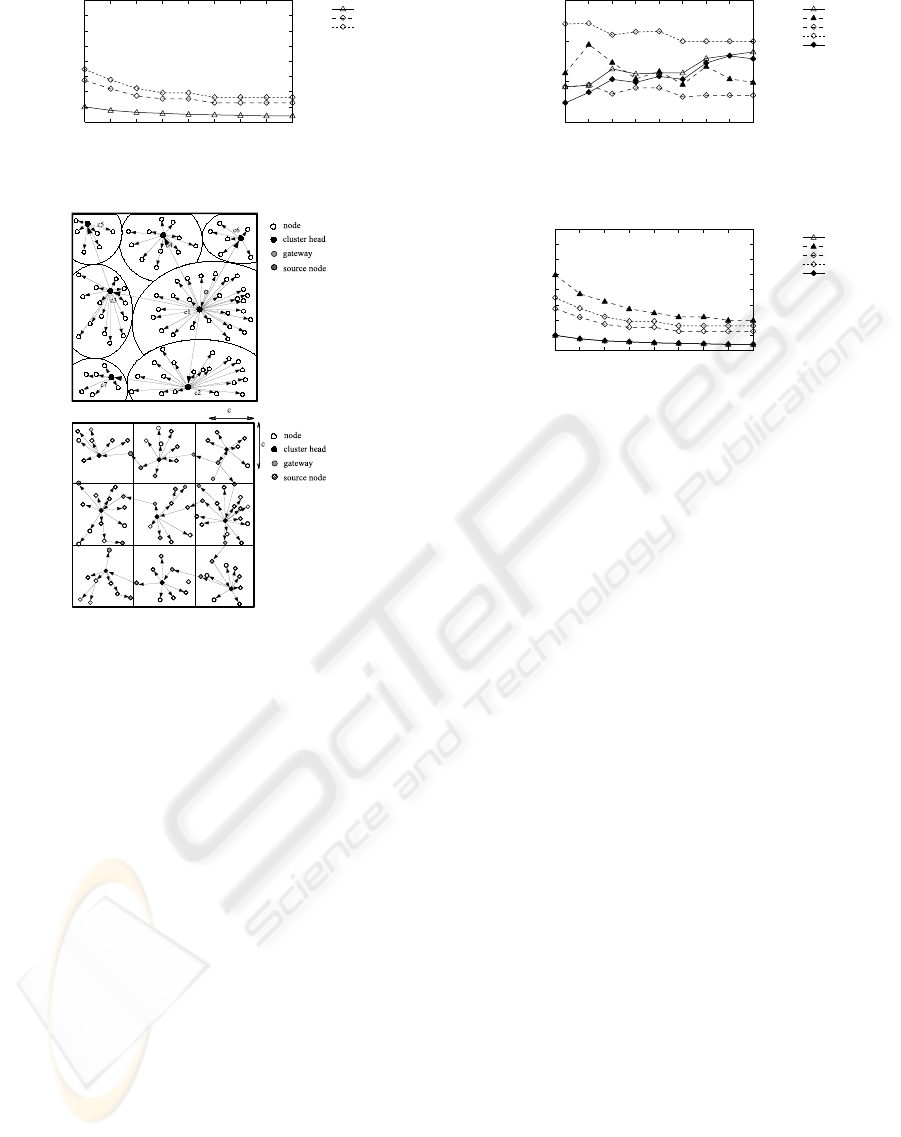
Further investigation in the following cases can be

considered: The k-clustering protocol adopts the di-

rect communication between adjacent cluster heads

WEBIST 2008 - International Conference on Web Information Systems and Technologies

238

100

120

140

160

100 200 300 400 500 600 700 800 900

Power of clusterhead

Number of node

mesh(4)

mesh(8)

Figure 7: Broadcasting power required in each cluster head.

Figure 8: Examples of broadcasting in new K-and lattice-

clustering.

(New k-clustering protocol). The lattice-clustering

protocol adopts mediate communications between ad-

jacent cluster heads (New lattice-clustering protocol).

We brieﬂy summarize the results in the case of these

new protocols. In the new lattice-clustering, a given

domain is divided by N X N lattices as is in the old

lattice-clustering protocol. In order to avoid an in-

crease in the number of gateways, the new proto-

col must take a certain measure, the details of which

are omitted in this paper due to space. The new k-

clustering protocol takes the same measure as in the

old k-clustering protocol. Fig. 8. shows examples of

broadcasting in new k- and lattice- clustering.

We evaluated the total energy consumption, the

average broadcasting powers of each head in Fig. 9

and 10, in 5 clustering protocols.

5 CONCLUSIONS

In this paper, we evaluated the energy efﬁciencies

for the broadcasts designed in both k-clustering and

lattice-clustering protocols. The evaluation showed

that the k-clustering protocol is characterized by the

30000

50000

70000

90000

100 200 300 400 500 600 700 800 900

Energy counsumption

Number of node

k(new)

mesh(4)

mesh(8)

mesh(new)

Figure 9: Comparison of the total energy consumption re-

quired in 5 clustering protocols.

100

120

140

160

100 200 300 400 500 600 700 800 900

Power of clusterhead

Number of node

k(new)

mesh(4)

mesh(8)

mesh(new)

Figure 10: Comparison of broadcasting power required in

each cluster head.

smallest broadcasting power of each node, and the

Lattice (4)-clustering protocol constitutes a charac-

teristic feature of the smallest total energy consump-

tion. The main source of the energy consumption in

k-clustering protocol is a large number of transmis-

sions between adjacent node pairs. Therefore, the ob-

tained results mean that, in the kind of communica-

tions such as those in broadcasting, direct communi-

cation between cluster heads should be also be taken

into the consideration. Further investigationshas been

performed for the new protocols: The k-clustering

protocol adopts direct communication between adja-

cent cluster heads, and the lattice-clustering proto-

col adopts mediate communications between adjacent

cluster heads.

REFERENCES

J. E. Wieselthier (2000). On the construction of energy-

eﬁcient broadcast and multicast tree in wireless net-

works.. IEEE INFOCOM.

V. Ravelomanana (2005). Distributed k-clustering algo-

rithms for random wireless multihop networks. IEEE

ICN.

Wu, J. and Dai, F. (2004). A distributed formation of a vir-

tual backbone in manets using adjustable transmission

ranges. IEEE ICDS.

EVALUATION OF K-/LATTICE-CLUSTERING ALGORITHMS FOR RANDOM WIRELESS MULTI-HOP

NETWORKS

239