COMBINED FUZZY SEMANTIC SIMILARITY MEASURE IN

OWL ONTOLOGIES

Vincenzo Cannella, Giuseppe Russo, Pierluca Sangiorgi and Roberto Pirrone

Universita’ degli Studi Palermo, Dipartimento Ingegneria Informatica - DINFO

Viale delle Scienze ed. 6 p.3, 90128 Palermo, Italy

Keywords:

Semantic Similarity Measure, OWL Ontologies, Semantic Web, Fuzzy Measure.

Abstract:

An algorithm is presented in this paper to calculate a semantic similarity measure inside an OWL ontology. The

formulation is based on a combined measure taking into account the two most important aspects involved in

the similarity computation. These are the structural properties of a concept, and the information content inside

the ontology. We deﬁne a fuzzy system to blend these information sources with a training process over some

ontologies. Finding a similarity measure between concepts of an ontology is a fundamental topic to accomplish

information exchange on the Web. Through this measure it is possible to perform sophisticated queries over

the web where the user is able to request concepts with a predeﬁned similarity (or even dissimilarity) degree.

1 INTRODUCTION

The deﬁnition of a measure for semantic similarity

is a very important task to accomplish in many pro-

cesses such as clustering and data mining, database

schema mapping, word sense disambiguation, infor-

mation indexing and information ﬁltering. Estima-

tion of semantic similarity measure in the same on-

tology (Gruber, 1993) or between distinct ontolo-

gies is a central need for the processes involving

the information exchange over the Web as deﬁned in

the cornerstone article from Tim Berneers-Lee about

the Semantic Web (Berners-Lee and Lassila, 2001)

(Berners-Lee et al., 2006). This work deals with a

possible deﬁnition of a semantic similarity measure

inside an ontology described through a OWL-DL ﬁle

(Helﬁn, 2004). OWL is the W3C standard for ontol-

ogy representation and is widely used in most appli-

cations over the web.

Deﬁning a semantic similarity measure requires a ﬁrst

agreement about the meaning of the term “similarity”.

In many works such as (Resnik, 1995) a terminolog-

ical clariﬁcation has been proposed. The more used

terms in the literature are similarity, relatedness and

distance. The distinction between similarity and re-

latedness regards the use of a functional relation be-

tween concepts. Two concepts are related if there is a

functional relation connecting them in some way. As

an example the subsumption relation (class-instance)

is a functional relation, and so is the meronymy re-

lation or whatever relation a user can deﬁne inside

a particular domain of interest. The distance term

is intended as the opposite of similarity. Semantic

distance, however, could be used with respect to dis-

tance between related concepts and distance between

similar concepts. The most used term in literature is

similarity but in this paper we refer to this term in a

broader way that is close to relatedness. The proposed

approach for this work is the deﬁnition and the imple-

mentation of a combined semantic similarity measure

to be computed on OWL-Dl ontologies. The proposed

measure is based on ontology structure and on the in-

formation provided by the attributes and the relations

that are deﬁned inside the ontology. For our purposes

similarity is deﬁned as follows: The more two con-

cepts are close in terms of their structural properties

and are correlated, the more they are similar. The

measure is a parametric one. Parameters tuning is

achieved by a fuzzy algorithm that mixes the com-

ponents of the measure deﬁnition.

The rest of the paper is arranged as follows: in the

next paragraph some related works are presented.

Third paragraph presents the proposed solution and

the algorithm. Next, some experimental results are

reported. Finally, some conclusions and future work

are presented.

181

Cannella V., Russo G., Sangiorgi P. and Pirrone R. (2008).

A COMBINED FUZZY SEMANTIC SIMILARITY MEASURE IN OWL ONTOLOGIES.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 181-186

DOI: 10.5220/0001522801810186

 SciTePress

2 RELATED WORKS

Many approaches have been proposed in literature to

deﬁne a measure for semantic similarity between con-

cepts. There are two fundamental categories of mea-

sures. The ﬁrst one is based on the topological dis-

tance between concepts in the ontology graph, while

the second one makes use of their information con-

tent. Some other approaches try to combine these two

aspects.

2.1 Graph Distance Models

A natural approach to deﬁne a measure in an ontol-

ogy is to use the distance between concepts because

an ontology is a graph where the edges represent rela-

tions between concepts and the nodes are the concepts

themselves. An earlier example of this measure was

proposed by (Rada et al., 1989) where the distance

between two concepts c

and c

is deﬁned as

dist(c

, c

) = min

p∈path(c

)

len

(p). (1)

where path(c

, c

) deﬁnes a possible path connect-

ing c

and c

. Starting from the Rada’s deﬁnition a

new measure is deﬁned in (Leacock and Chodorow,

1998) where some adjustments are adopted. The ma-

jor problem of this approach is related to the consid-

eration that all the edges in the graph represent uni-

form distances. This assumption is trivially wrong

when dealing with an ontology where the edges along

the path between two concepts can represent different

levels of generalization. So they cannot be assumed

to have the same weight in computing the distance.

Concepts with different depth with respect to the root

node are differently related. The more they are gen-

eral the more they are distant. A natural solution is

to weight the path with some function that takes into

account also the depth level of the concept. In (Wu

and Palmer, 1995) a measure is presented as the sum

of two different values.

sim(c

, c

) =

2 ∗ minlen

comm

)

minlen

(p) + 2min len

comm

)

. (2)

where len

comm

) is an intermediate distance deﬁned

starting from the most common subsumer of the two

nodes. Most recent approaches like (Castano et al.,

2004) concentrate their focus on the determination

of the weights related to the relation with neighbor

nodes.

2.2 Information Theory Models

The models inspired to information theory require

some additional information to deﬁne the similarity

measure. Usually the information is given by a cor-

pus of documents related to the ontology. In (Resnik,

1995) a measure is deﬁned on the following hypoth-

esis: the more two concepts share common informa-

tion, the more they are similar. The formulation for

the similarity is the following:

sim(c

, c

) = max

c∈S(c

)

[−log p

]. (3)

Where S is the set of concepts that subsumes both c

and c

. The frequency p

of the concept inside the

corpus, gives the added information value. In (Jiang

and Conrath, 1997) the distance between two con-

cepts is computed as the difference between the sum

of the information content of the two concepts and

the information content of their most speciﬁc com-

mon subsumer. In (Lin, 1999) a similarity that takes

into account the information shared by two concepts,

like Resnik, but also the difference between them is

proposed.

2.3 Combined Models

Another possible approach is to combine the previ-

ously presented techniques, to gain the beneﬁts pro-

vided by both the models. The structural approach for

ontologies expressed in OWL is restrictive because an

OWL ﬁle contains many information about classes,

attributes and relations that can be used. Furthermore

a combined approach can overcome some problems

due to the facts that in an ontology both structural

and information based contents are relevant. This ap-

proach seems to be very promising and is the one used

in our work. In (Nguyen and Al-Mubaid, 2006) a new

measure for similarity is deﬁned, which uses a new

feature called common speciﬁcity (CSpec) besides the

path length feature. The CSpec feature is derived from

the information content obtained from single concepts

and the overall ontology, given a related document

corpus. The formulation is:

CSpec(c

, c

) = IC

max

− IC(LCS(c

, c

)). (4)

where IC

max

is the maximum IC (ontology informa-

tion content) of concept nodes in the ontology and

LCS(c

, c

) is the least common subsumer of c

and

In (Wang et al., 2006) the HIC-AIC algorithm to com-

pute similarity is presented, which is based on hierar-

chal information content (HIC) and attributes infor-

mation content (AIC). This approach deﬁnes the sim-

ilarity measure as the sum of the two values starting

from an useful ontology model deﬁnition that we have

extended.

WEBIST 2008 - International Conference on Web Information Systems and Technologies

182

3 PROPOSED SOLUTION

3.1 Ontology Deﬁnition

As previously stated, the structure-based and

information-based methods for similarity calculation

depend on the ontology structure and neglect many

information such as relations and attributes. In

the following an approach based on hierarchical

content and behavioral information content is pre-

sented. The used ontology model deﬁnition that

is suitable for our purposes is a 6-tuple deﬁned as:

O = {C, R, A, H

, att, rel} where:

• C: concepts set.

• R: relations set.

• A: attributes set.

• H

: hierarchy structure, is a particular relation

called concept taxonomy. H

, c

) means that

is a sub-concept of c

• att: the concept-attribute function. It relates the

concepts of set C and the attributes of set A.

att(c

, a

) means that c

has an a

attribute.

• rel: the concept-relation function. It relates the

concepts of set C and the relations of set R.

rel(c

, r

) means that c

has a r

relation that con-

nect it with other concepts.

In this model only the functional part of ontologies

is explicitly stated, while the descriptive one is dis-

carded. This is formed by the lexicon of concepts, the

relations and the mapping functions of the functional

and descriptive parts. The purpose is to have a

clear description and to focus the attention to really

signiﬁcant terms to be used in practice.

3.2 Assumptions and Deﬁnitions

The proposed solution is based on some reasonable

assumptions about the domain that are summarized in

the following. The deﬁnitions are reported to help the

explanation of some crucial aspects of the solution.

Assumption 1: Given two concepts c

and c

, if a

an attribute of c

and c

is a sub-concept of c

, then

is an attribute of c

. In other words, a sub-concept

inherits all the attributes of his father node.

Assumption 2: Given two concepts c

and c

, if c

has

a r

relation and c

is a sub-concept of c

, then c

has

a r

relation. In other words, a sub-concept inherits

all the direct relations of his father node.

Deﬁnition 1: Ancestor, denoted as Ancestor(c

, c

Given three concepts c

, c

and c

, if c

is a sub-

concept of c

or c

is a sub-concept of c

and c

a sub-concept of c

or c

is a sub-concept of c

and c

is an ancestor of c

then c

is an ancestor of c

Deﬁnition 2: Most Recent Common Ancestor, de-

noted as MRCA(c

, c

). Given two concepts c

and

, the most recent common ancestor of c

and c

the concept c which is ancestor of both c

and c

and

has the minimum number of ancestors of c

and c

its descendants nodes.

Deﬁnition 3: Common Attribute, denoted as

CA(a

, c

). Given two concepts c

e c

, if a

is an

attribute of c

and c

, then a

is a common attribute

of c

and c

Deﬁnition 4: Common Relation, denoted as

CR(r

, c

). Given two concepts c

and c

, if r

is a relation of c

and c

, then r

is a common relation

of c

and c

Deﬁnition 5: Not-Inherited Common Attribute, de-

noted as NICA(a

, c

). Given two concepts c

and

, if a

is a common attribute of c

and c

, and a

isn’t an attribute of the most recent common ancestor

of c

and c

, then a

is a not-inherited common at-

tribute of c

and c

Deﬁnition 6: First Child of Most Recent Common

Ancestor, denoted as FCM(c

, c

). Denotes the

ﬁrst concept c

to cross starting from the Most Re-

cent Common Ancestor(c

, c

) to reach the concept

through the shortest path between the concepts c

and c

. FCM(c

, c

) denotes the other concept

child c

to cross reaching the concept c

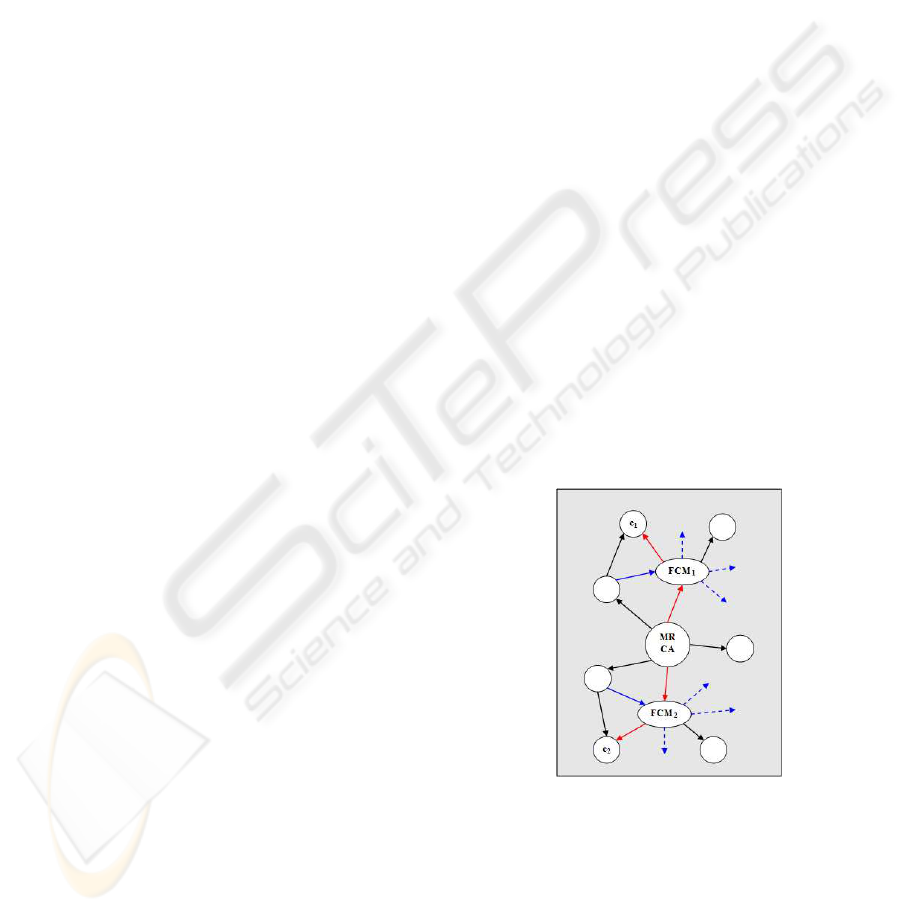
Figure 1: A typical ontology fragment.

Figure 1 shows a fragment of an ontology where it is

possible to see the two concepts to compare, the most

recent common ancestor, his ﬁrst child, the shortest

path between c

and c

through is-a relations (high-

lighted in red) and the relations of the two children

to be compared (highlighted in blue). Starting from

these deﬁnitions we are able to formalize our algo-

rithm for the semantic similarity measure.

A COMBINED FUZZY SEMANTIC SIMILARITY MEASURE IN OWL ONTOLOGIES

183

3.3 Proposed Algorithm

The proposed method is based on the assumption that

“two concepts are much more similar how less distant

and more correlated among them they are”. This sim-

ple deﬁnition makes intuitive the use of a fuzzy sys-

tem (Zadeh, 1992) to produce a similarity measure of

two concepts as a function of distance and correlation.

The measure will range in [0, 1].

The distance component is deﬁned by the following:

dist(c

, c

) = ShortestWeightedPath(c

, c

). (5)

This term is based on a structural approach (Graph

Distance Model). It denotes the distance between two

ontology concepts. It’s expressed as the minimum

weighted sum of relations crossed to reach c

from

The correlation component is given by:

corr(c

, c

) =

1 +

∗

1 +

(6)

where N

is the number of NICAs of c

and c

, T

the total number of attributes of c

and c

, N

is the

number of the CRs of FCMs of c

and c

, T

is the

total number of relations of the FCMs of c

and c

This term is based on a behavioral approach and de-

notes the correlation between two ontology concepts

in terms of their specialization considering the func-

tional aspect given by attributes and relations. In our

scenario, we consider that two concepts are corre-

lated, in a behavioral sense, “if they are able to ex-

press something similar”. The expression in (6) is

made by two gain terms. It means that correlation

increases if c

and c

share many attributes not inher-

ited from their MRCAs and if their ancestors share

many relations. This is a global measure of how c

and c

carry a similar information content. The rela-

tions to consider in this formula are only those giving

an informative contribution, while structural informa-

tion (like is-a, subclass-of, etc) is neglected. To pro-

ceed in measuring similarity, we have to estimate at

ﬁrst the relevant terms like ancestors, common and

not common attributes, common and not common re-

lations. In this way, we are able to measure Distance

and Correlation. These two values are used as crisp

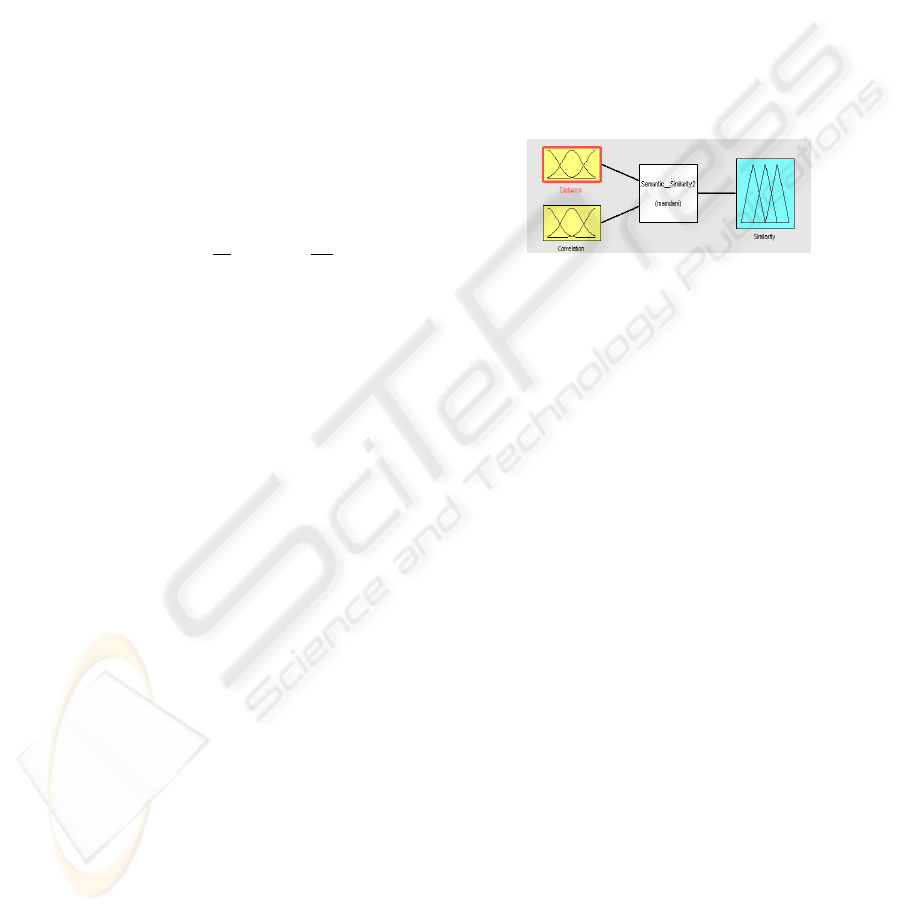
inputs in a fuzzy system (see Fig 2). We deﬁned the

fuzzy sets for the inputs and the similarity output us-

ing the following fuzzy rules:

• IF closed AND correlated THEN very similar

• IF closed AND average correlated THEN similar

• IF closed AND not correlated THEN average sim-

ilar

• IF far AND not correlated THEN very dissimilar

• IF far AND average correlated THEN dissimilar

• IF far AND correlated THEN average dissimilar

• IF average closed AND correlated THEN similar

• IF average closed AND average correlated THEN

average similar

• IF average closed AND not correlated THEN av-

erage dissimilar

We used Gaussian membership functions for the in-

puts, while the output has triangular one. Crisp simi-

larity is obtained from the output fuzzy set using the

centroid rule.

Figure 2: The Fuzzy System.

The proposed algorithm is based on measure combin-

ing the well known structural approach, the Shortest

Weighted Path, and an information-based one, which

relies on behavioral considerations about the concepts

in the ontology. In particular, the second term of

the measure estimates the behavioral specialization of

each node inside the ontology. This result considering

the analysis of attributes and relations. Differently

from other related works, relations inside the ontol-

ogy have particular relevance for the algorithm. Re-

lations are able to provide information regarding not

only the ontology structure, but also the contents the

ontology deals with.

3.4 Experimental Results

Before performing experiments the fuzzy system has

to be trained to tune the parameters of the membership

functions belonging to the fuzzy sets. For the training

phase we used some ontologies taken from a selection

of OWL ontologies (Protege’, 2004). Such ontologies

have been speciﬁcally developed for the Semantic

Web and provided by the Protege’ team of the Stan-

ford Medical Informatics at the Stanford University

School of Medicine. We have trained our fuzzy sys-

tem using the Matlab Fis Editor module to check our

fuzzy rules and to ﬁnd the appropriate membership

functions for the two input variables Distance and

Correlation and the output variable Similarity. Fig-

ures 3, 4, 5 show the membership functions adopted

for these three values.

WEBIST 2008 - International Conference on Web Information Systems and Technologies

184

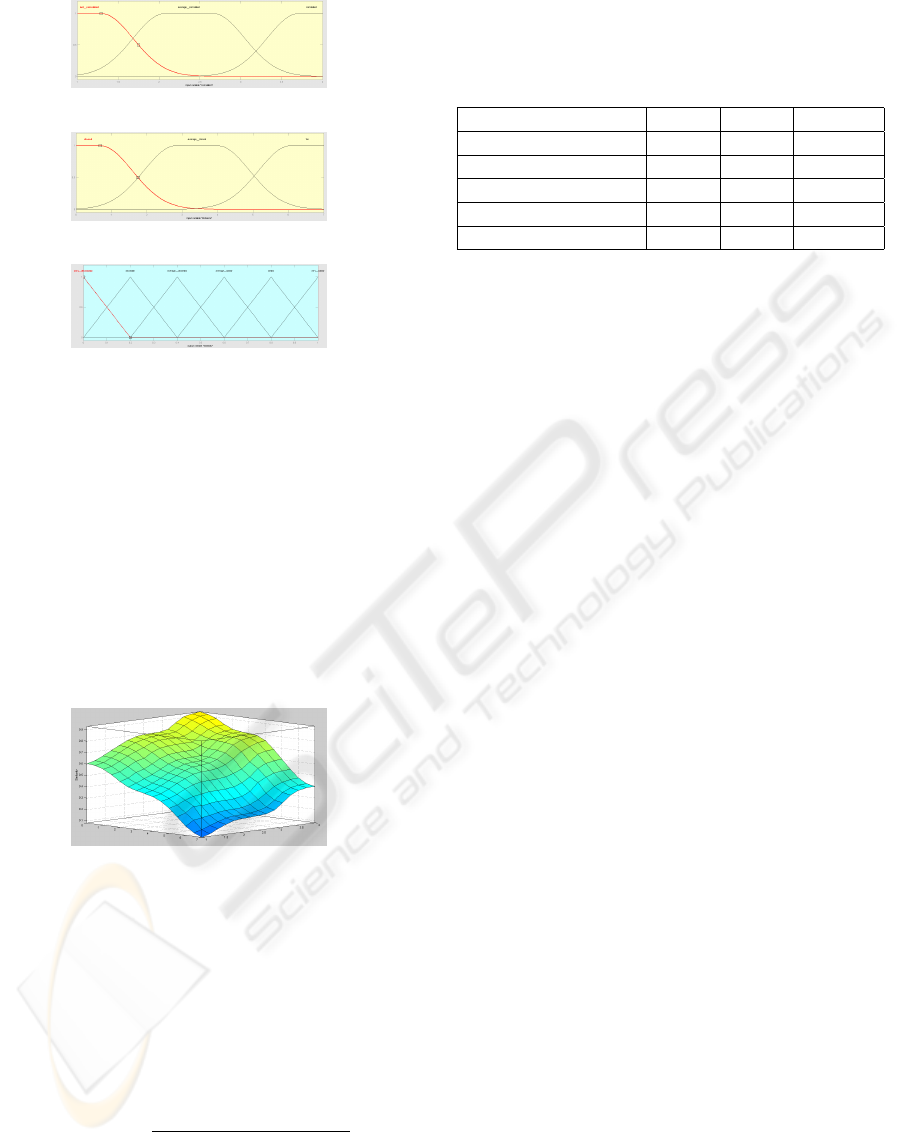
Figure 3: Correlation.

Figure 4: Distance.

Figure 5: Similarity.

We did not manipulate the output membership

functions for Similarity. We used standard triangu-

lar functions equally distributed over the whole range.

This prevents the system from over-ﬁtting particular

ontological structures. In this way we let the system

free to adapt to those cases when the user wants to

enhance the contribution of a single input variable

(Correlation or Distance) according to the arrange-

ment of the ontology under investigation. Figure 6

shows the surface describing the Similarity distribu-

tion, which reﬂects the adoption of equally spaced

membership functions. We tested the method on an

Figure 6: Surface Similarity Distribution.

ontology about the tourism domain contributed by

Holger Knublauch. This ontology is composed by 35

concepts, 21 attributes of 6 different types, 20 rela-

tions and its graphical representation is shown in ﬁg-

ure 7.

Finally, we have compared the results with

Resnik’s algorithm and Lin’s algorithm using respec-

tively the equation (3) and the equation (7) below.

sim(c

, c

) =

2 ∗ log(P(C))

log(P(C

)) + log(P(C

))

. (7)

In the literature these measures usually includes a

concept when computing its offspring. We excluded

the parent from the computation of its offspring due to

the use of OWL ontologies where the super-concept

owl:Thing

is deﬁned by default. The results are

shown in the following table:

Table 1: Experimental Results.

Concept 1 - Concept 2 R. Sim L. Sim F. C. Sim

Capital - National Park 0.640 0.640 0.404

Bunjee Jumping - Surf 0.502 0.502 0.454

Destination - Acc. 0.012 0.015 0.490

Museum - Town 0.012 0.012 0.195

Beach - City 0.640 0.503 0.511

The obtained values need to be explained in detail

because of the different interpretation with respect to

the other methods. This approach is able to carry out

the semantic aspect considering the domain of the on-

tology and making a measure related to the context.

Let’s consider the result obtained in semantic sim-

ilarity between Accommodation and Destination con-

cepts. Generally, we can say that this two terms are

dissimilar and traditional methods conﬁrm that, but

if we consider this terms in an appropriate context,

they could be semantically similar (related). In our

experimental domain about tourism they share the re-

lation hasAccommodation - hasDestination and result

more similar respect to traditional methods that ne-

glect the relations. We propose this as a better ap-

proach to Semantic Web technologies in System Inte-

gration, where using domain aspects is a crucial topic

for a good optimization of the systems. The evalua-

tion of the distribution of semantic similarity values

in the surface (see Fig. 6) gives the possibility to

set many different thresholds to discriminate the sim-

ilar concepts to be presented to users. The measure

is not linear and the attention is focused on [0.4 0.7]

range. As an example the value 0.404 between Cap-

ital and National Park in the domain is just over the

minimum range acceptable (0.4) if we want to present

more additional information. The value 0.454 be-

tween Bunjee-Jumping and Surf like the value 0.511

for Beach-City are acceptable and are the result of

the improvement given by the combined measure.

The ﬁrst couple is closer so the structural contribu-

tion gives an higher similarity value while the second

couple shares a relation. The obtained surface makes

clear that for our purposes it is possible to add addi-

tional and pertinent results, related to context as de-

creasing rating to end users that make queries in these

systems.

3.5 Conclusions and Future Work

In this paper an algorithm to calculate a semantic

similarity measure inside an OWL ontology was pre-

sented. This similarity method is based on a fuzzy

A COMBINED FUZZY SEMANTIC SIMILARITY MEASURE IN OWL ONTOLOGIES

185

Figure 7: A view of the ontology.

mix of a behavioral information approach and a struc-

tural one. The proposed measure results efﬁcient

when it is used in ontologies with many relations apart

of the structural ones (is a, part of, etc.). Thanks to

relations, is possible to retrieve signiﬁcant results for

the used domain, otherwise neglected by other meth-

ods. Our future work will provide an extension in the

similarity calculation using all the properties of the

OWL ontologies like the deﬁnition of union, intersec-

tion, restriction and all the other properties provided

from the OWL standard. We are also trying tho inte-

grate the proposed algorithm in a complete system at

the presentation level to obtain replies that are richer

than in the typical SPARQL environments.

REFERENCES

Berners-Lee, T. and Lassila, O. (2001). The semantic web.

In Scientiﬁc American.

Berners-Lee, T., Shadbolt, N., and Hall, W. (2006). The

semantic web revisited. In IEEE Intelligent Systems.

Castano, S., Ferrara, A., Montanelli, S., and Racca, G.

(2004). Semantic information interoperability in open

networked systems. In Proc. of the Int. Conference on

Semantics of a Networked World (ICSNW), in cooper-

ation with ACM SIGMOD 2004.

Gruber, T. R. (1993). A translation approach to portable

ontology speciﬁcations. In Knowledge Acquisition.

Helﬁn, J. (2004). Web ontology language (owl): Use cases

and requirements. In W3C Recommendation.

Jiang, J. J. and Conrath, D. (1997). Semantic similarity

based on corpus statistics and lexical taxonomy. In

Proceedings of International Conference on Research

in Computational Linguistics.

Leacock, C. and Chodorow, M. (1998). Combining local

context and wordnet similarity for word sense identi-

ﬁcation. In WordNet: An electronic lexical database.

MIT Press.

Lin, D. (1999). An information-theoretic deﬁnition of sim-

ilarity. In Proceedings of the 15th International Con-

ference on Machine Learning. Morgan Kaufmann.

Nguyen, H. and Al-Mubaid, H. (2006). A combination-

based semantic similarity measure using multiple in-

formation sources. In IEEE International Conference

on Information Reuse and Integration.

Protege’ (2004). Protege’ ontology library.

http://protegewiki.stanford.edu/index.php/. [On-

line; accessed October 2007].

Rada, R., Mili, H., Bicknell, E., and Blettner, M. (1989).

Development and application of a metric on seman-

tic nets. In IEEE Transactions on Systems, Man, and

Cybernetics.

Resnik, P. (1995). Using information content to evaluate se-

mantic similarity in a taxonomy. In Proceedings of fhe

fhe International Joint Conference on ArtiﬁciaI Intel-

ligence (IJCAI).

Wang, G.-H., Wang, Y.-D., and Guo, M.-Z. (2006). An

ontology-based method for similarity calculation of

concepts in the semantic web. In IEEE International

Conference on Machine Learning and Cybernetics,

pages 100–105.

Wu, Z. and Palmer, M. (1995). Verb semantics and lexical

selection. In Proceedings of32nd Annual Meeting of

the Associations for Computational Linguistics.

Zadeh, L. A. (1992). Knowledge representation in fuzzy

logic. In Yager, R. R. and Zadeh, L. A., editors, An

Introduction to Fuzzy Logic Applications in Intelligent

Systems, pages 1–25, Boston. Kluwer.

WEBIST 2008 - International Conference on Web Information Systems and Technologies

186