A FAST COMMUNITY BASED ALGORITHM FOR

GENERATING WEB CRAWLER SEEDS SET

Shervin Daneshpajouh, Mojtaba Mohammadi Nasiri ¹

Computer Engineering Department, Sharif University of Technology, Tehran, Iran

Mohammad Ghodsi ²

Computer Engineering Department, Sharif University of Technology, Tehran, Iran

School of Computer Science, Institute for Studies in Theoretical Physics and Mathematics, Tehran, Iran

Keywords: Crawling, Communities, Seed Quality Metric, Crawl Quality Metric, HITS, Web Graph, Hyperlink

Analysis.

Abstract: In this paper, we present a new and fast algorithm for generating the seeds set for web crawlers. A typical

crawler normally starts from a fixed set like DMOZ links, and then continues crawling from URLs found in

these web pages. Crawlers are supposed to download more good pages in less iterations. Crawled pages are

good if they have high PageRanks and are from different communities. In this paper, we present a new

algorithm with O(n) running time for generating crawler's seeds set based on HITS algorithm. A crawler

can download qualified web pages, from different communities, starting from generated seeds set using our

algorithm in less iteration.

1 INTRODUCTION

A major question a crawler has to face is which

pages are to be retrieved to have the "most suitable"

pages in a collection (Henzinger, 2003). Crawlers

normally retrieve a limited number of pages. In this

regard, the question is how fast a crawler collects the

"most suitable" pages. A unique solution to this

question is not likely to exist.

Different algorithms with different metrics have

been suggested to lead a crawl towards high quality

pages (Cho et al., 1998), (Najork, 2001). In (Cho et

al., 1998) Cho, Garcia-Molina, and Page suggested

using connectivity-based metrics. To direct a crawl,

they have used different ordering metrics: breadth-

first, backlink count, Page Rank (Brin and Page,

1998), and random. They have revealed that

performing a crawl in breadth-first order works

nearly well if "most suitable" pages are defined to be

pages with high PageRanks.

Najork and Wiener extended the results of Cho et

al. They examined the average page quality over the

time of pages downloaded during a web crawl of

328 million unique pages and showed that traversing

the web graph in breadth-first search order is a good

crawling strategy(Najork, 2001).

Based on Henzinger's work (Henzinger, 2003)

better understanding of graph structure might lead to

a more efficient way to crawl the web. In this paper,

we use this idea to develop our algorithm. First, we

define the "most suitable" pages and then show how

a crawler can retrieve them. We use three metrics to

measure the quality of a page.

We also present a new fast algorithm for

extracting seeds set from previously crawled pages.

Using offered metrics, we show that starting from

extracted seeds suggested by our algorithm, a

crawler will quickly collect the most suitable pages

from different communities.

From the study of different community

extraction algorithms: PageRank, Trawling, HITS,

and Network flow base community discovery, we

decided to use HITS-Ranking without keyword

search for community discovery and collecting

seeds set. We have found that bipartite cores are

useful for selecting seeds set. Bipartite cores contain

¹ This author's work was in part supported by a grant from

ITRC (N. T-500-1895-86-2-17.)

² This author's work was in part supported by a grant from

IPM (N. CS2386-2-01.)

Daneshpajouh S., Mohammadi Nasiri M. and Ghodsi M. (2008).

A FAST COMMUNITY BASED ALGORITHM FOR GENERATING WEB CRAWLER SEEDS SET.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 98-105

DOI: 10.5220/0001527400980105

 SciTePress

Hub and Authority pages. Since we are interested in

having Authority pages in our crawl, we would need

to start crawling from Hub pages. Hubs are durable

pages, so we can rely upon them for crawling.

The main idea in our method is to use HITS-

Ranking on the whole graph for extracting the most

important bipartite cores. We offer two bipartite core

extraction algorithms.

We have compared the results of the crawls

starting from our extracted seeds set with crawls

starting random nodes. Our experiments show that

the crawl starting from our seeds finds the most

suitable pages of web very faster.

To the best of our knowledge, this is the first

such seeds extraction algorithm. The running time of

proposed algorithm is O(n). Low running time with

community base properties makes this algorithm

unique in comparison with previous algorithms.

2 DISCOVERING SEEDS SET IN

LARGE WEB GRAPH

A crawler usually retrieves a limited number of

pages. Crawlers are expected to collect the "most

suitable" pages of web rapidly. We define the "most

suitable" pages of web as those pages with high

Page Rank. In terms of HITS algorithm, these are

called Authority pages. The difference is that HITS

finds the authority pages relating to keywords but

PageRank shows the importance of a page in the

whole web. We know that good hubs link to good

authorities. If we are able to extract good hubs from

a web graph and different communities, we will be

able to download good authorities that have high

PageRank of different communities.

2.1 Iterative HITS-Ranking & Pruning

We assume that we have the crawled web graph.

The goal is to extract seeds set from this graph so

that a crawler can collect the most important pages

of the web in less iteration. To do this we run HITS-

Ranking algorithm on this graph. This is the second

step of HITS algorithm. In the first step, it searches

the keywords in an index-based search engine. For

our purpose, we ignore this step and only run the

ranking step on the whole graph. In this way,

bipartite cores with high Hub and Authority rank

will become visible in the graph. Then, we select the

most highly ranked bipartite core using two

algorithms. We suggest, extracting seeds with fixed

size, and extracting seeds with fixed density; we

remove this sub-graph from the graph, repeat

ranking, seed extraction, and sub-graph removal

steps up to a point that we have enough seeds set.

Why do we run HITS-Ranking repeatedly? The

answer is: removing bipartite core in each step

modifies the web-graph structure. In fact, re-ranking

changes the hub and authority ranks of bipartite

cores. Removing high-ranked bipartite core and re-

ranking web-graph drive, bipartite cores appeared to

be from different communities. Thus, a crawler will

be able to download pages from different

communities starting from these seeds. Our

experiments prove that extracted bipartite cores have

a reasonable distance from each other.

We expect to crawl the most suitable pages,

because, in iterations of algorithm, we select and

extract high-ranked bipartite cores which have high

hub or authority ranks. It is expected that such pages

link to pages with high PageRank. Our experiments

prove the correctness of this hypothesis.

2.2 Extracting Seeds with Fixed Size

The procedure in Figure 1, extracts one bipartite

sub-graph with highest hub and authority ranks with

predetermined size given as an input. The procedure

is given a directed graph G, BipartiteCoreSize,

NewMemberCount and h, and a vectors.

BipartiteCoreSize specifies the desired size of

bipartite core we like to be extracted.

NewMemberCount indicates in each iteration of

algorithm how many hub or authority nodes should

be added to the hub or authority sets; h and a vectors

are hub and authority ranks of nodes in the input

graph G.

In the initial steps, the Algorithm sets HubSet to

empty and adds the node with highest authority rank

to AuthoritySet. While the sum of AuthoritySet size

and HubSet size is less than BipartiteCoreSize, it

continues to find new hubs and authorities regarding

the NewMemberCount and adds them to the related

set. We use this procedure when we like to extract

bipartite sub-graph with fixed size. Figure 1 shows

the details of this procedure. An interesting result we

have found in our experiments is that at the very first

steps, all the hubs have links to all authorities which

is a complete bipartite sub-graph. This leaded us to

suggest a density base extraction algorithm.

2.3 Extracting Seeds with Fixed

Cover-Density

The procedure in Figure 2 extracts one bipartite sub-

graph with highest hub and authority ranks in a way

A FAST COMMUNITY BASED ALGORITHM FOR GENERATING WEB CRAWLER SEEDS SET

that the sub-graph has the desired cover-density

function.

We define Cover-Density as follows:

(1)

||||

|),(|

*100

etAuthoritySHubSet

etAuthoritySHubSetE

This measure shows how many nodes in the

authority set are covered by nodes in hub set.

In initial steps, procedure sets HubSet to empty

set and adds the node with highest authority rank to

AuthoritySet. In addition, it sets CoverDensityCur to

100.

While CoverDensityCur is bigger than or equal

to input CoverDensity, procedure continues to find

new hubs and authorities. This algorithm adds only

one new node to the sets at each iteration of the

algorithm. If we increase the number of new nodes

to more than 1, this might cause the reduction of the

accuracy of desired cover density.

Figure 1: Extracting Bipartite Cores with Fixed Size.

2.4 Putting it All Together

Up to now, we have presented algorithms for HITS-

Ranking and bipartite core extraction based on hub

and authority ranks. Our goal is to extract a set of

desired number of seeds to crawl and download

pages from different web communities with high

PageRank in less iteration. We use the proposed

algorithms to achieve this goal. We assume that we

have a crawled web graph. Then we run HITS-

Ranking algorithm on the whole graph and use one

of the bipartite core extraction algorithms we have

presented. Then, we select arbitrarily one of the

nodes in the extracted hub set and add it to our seeds

set. Finally, we remove the extracted core from the

input graph and repeat these steps until we find the

ideal number of seeds.

We can use one of these two bipartite core

extraction algorithms that we have proposed:

Extract-Bipartite-Cores-with-Fixed-Size, Extract-

Bipartite-Cores-with-Fixed-CoverDensity. If we

wish bipartite cores to have a fixed size we use the

first algorithm and if we are looking for bipartite

cores having desired cover density, then we use the

second algorithm.

Figure 2: Extracting Bipartite Cores with Fixed Density.

We have experimented both of these algorithms.

As we cannot guess the suitable size of a web

community, we use the second method. The second

method can calculate the density of links between

hubs and authorities. If we have a complete bipartite

core then we are sure that all the authority pages are

Procedure Extract-Bipartite-Cores-with-Fixed-Size

Input: graph: G=(V,E) , integer:

BipartiteCoreSize, NewMemberCount;

vector: h,a.

1) HubSet =

∅

;

2) AuthoritySet= Add v with highest a(v) to

AuthoritySet;

3) While |AuthoritySet| + |HubSet| <

BipartiteCoreSize do

4) HubSet = HubSet ∪ (Find Top

NewMemberCount h(v) where v,w∈ E

and w in AuthoritySet and v not in

HubSet);

5) AuthoritySet= AuthoritySet ∪ (Find Top

NewMemberCount a(v) where w,v∈ E

and v in AuthoritySet and w not in

HubSet );

6) End While

output: HubSet, AuthoritySet

End Procedure

Procedure Extract-Bipartite-Cores-with-Fixed-

CoverDensity

Input: graph: G=(V,E) , integer:

CoverDensity;

vector: h,a.

1) HubSet =

∅

;

2) AuthoritySet = Add v with highest a(v) to

AuthoritySet;

3) CoverDensityCur = 100;

4) While CoverDensityCur ≥ CoverDensity do

5) HubSet = HubSet ∪ (Find Top

NewMemberCount h(v) where v,w∈

and w in AuthoritySet and v not in

HubSet);

6) AuthoritySet= AuthoritySet ∪ (Find

Top NewMemberCount a(v) where

w,v∈ E and v in AuthoritySet and w

not in HubSet );

7) CoverDensityCur =

||||

|),(|

*100

etAuthoritySHubSet

etAuthoritySHubSetE

;

8) End While

output: HubSet, AuthoritySet

End Procedure

WEBIST 2008 - International Conference on Web Information Systems and Technologies

100

from the same community. By decreasing the Cover-

Density measure, we decrease the degree of

relationship between authority pages. Because the

second method is more reliable than the first one, in

this paper we only present experimental results

achieved from using Extract-Bipartite-Cores-with-

Fixed-CoverDensity. The Extract-Seeds procedure

(Figure 3) use this bipartite core extraction algorithm

to return a valuable seeds set.

Figure 3: Seeds Extraction Algorithm.

The Extract-Seeds algorithm receives a directed

graph G and SeedCount as input. At the initial step,

algorithm sets SeedSet to empty. While the size of

SeedSet is less than SeedCount, the algorithm keeps

running. In the first line of While section, algorithm

calls HITS-Ranking procedure with G as the input

graph and 60 as HITSIterationCount. Kleinberg's

work shows that HITSIterationCount equal to 20, is

enough for convergence of hub and authority ranks

in a small sub-graph (Jon M. Kleinberg, 1999). We

have found experimentally that a number of more

than 50 is enough for convergence of hub and

authority ranks with the dataset we use. HITS-

Ranking algorithm returns two vectors, h and a,

containing result of hub and authority ranks of all

nodes in graph G. In the next line algorithm calls

Extracting-Bipartite-Cores-with-Fixed-CoverDensity

with G as input graph, 100 as cover density value,

and h and a as hub and authority vectors. This

function finds complete bipartite cores in the input

graph and returns complete bipartite nodes in

HubSet and AuthoritySet. In the next line, a node

randomly is selected from hub set and is added to

the SeedSet. Now algorithm removes the hub and

authority nodes and their edges from graph G. The

removal step helps us to find seeds from different

communities.

2.5 Complexity of Proposed Seeds

Extraction Algorithm

The running time of Seeds-ExtractionAlgorithm,

(Figure 3), is O(n), where n is the number of nodes

in the input graph.

The While loop of lines 2-12 is executed at most

|SeedCount| times. The work of line 4 is done in

O(n). Because the complexity of HITS-Ranking is

equal to

(K*2*L*n) where L the average number

of neighborhoods of a node, K |HitsIterationCount|,

and n is the number of nodes in the input graph. This

complexity is multiplied by 2 because there are two

steps for this kind of computation, one for hub

vector and the other for authority vector. In addition,

the normalization steps can be done in

(3n). So,

the complexity of HITS-Ranking is O(n).

The running time of Extracting-Bipartite-Cores-

with-Fixed-CoverDensity in line 4 is O(n). The

While loop of lines 4-8, in figure 2, is executed at

most |HubSet + AuthoritySet| times which can be

viewed as a constant number k. Finding and adding a

distinct hub node with highest rank to hub set, in line

5, takes

(k*n). Finding and adding a distinct

authority node with highest rank to authority set, in

line 6, takes

(k*n). So, the running time of

Extracting-Bipartite-Cores-with-Fixed-

CoverDensity is at most O(n).

The removal steps of lines 6-11, in Figure 3,

takes O(n) for removing identified hubs and

authorities.

Therefore, the total running time of Seed-

Extraction Algorithm is O(|SeedCount|*n), which is

equal to O(n).

3 EXPERIMENTAL RESULTS

In this section, we apply our proposed algorithm, to

find seeds set from previously crawled pages. Then,

we start a crawl using extracted seeds on the same

graph to evaluate the result. To show how applying

algorithm on old data can provide good seeds for a

new crawl, we start the crawl on a newer graph

using seeds set extracted from a previous crawl.

Procedure Extract-Seeds

Input: graph: G=(V,E) , integer: SeedCount;

1) SeedSet = ∅

2) While |SeedSet| < SeedCount do

3) h, a = HITS-Ranking( G , 60);

4) HubSet, AuthoritySet = Extracting-

Bipartite-Cores-with-Fixed-

CoverDensity(G, 100, h, a);

5) SeedsSet = SeedsSet ∪ Select a node

arbitrarily from HubSet;

6) For all v in HubSet do

7) Remove v and all E(v) from G;

8) End For

9) For all v in AuthoritySet do

10) Remove v and all E(v) from G;

11) End For

12) End While

output: SeedsSet

End Procedure

A FAST COMMUNITY BASED ALGORITHM FOR GENERATING WEB CRAWLER SEEDS SET

101

3.1 Data Sets

The laboratory for Web Algorithmics at the

University of Milan provides different web graph

data sets (Laboratory for Web Algorithmics, 2007).

In our experiments, we have used UK-2002 and UK-

2005 web graph data sets provided by this

laboratory. These data sets are compressed using

WebGraph library. WebGraph is a framework for

studying the web graph (Boldi and Vigna, 2004). It

provides simple ways to manage very large graphs,

exploiting modern compression techniques. With

WebGraph, we can access and analyze a very large

web graph on a PC.

3.1.1 UK-2002

This data set has been obtained from a 2002 crawl of

the .uk domain performed by UbiCrawler in 2002

(Boldi et. al, 2004). The graph contains 18,520,486

nodes and 298,113,762 links.

3.1.2 UK-2005

This data set has been obtained from a 2005 crawl of

the .uk domain performed by UbiCrawler in 2005.

The crawl was very shallow, and aimed at gathering

a large number of hosts, but from each host a small

number of pages. This graph contains 39.459.935

nodes and 936,364,282 links.

3.2 Data Set Characteristics

3.2.1 Degree Distribution

We had investigated the degree distribution of UK-

2002 and UK-2005. The results show that the In-

degree and Out-degree distribution are power laws

in these two datasets.

3.2.2 Diameter

The diameter of a web-graph is defined as the length

of shortest path from u to v, averaged over all

ordered pairs (u,v) (Albert et. al, 2000). Of course,

we omit the infinite distance between pairs that there

is not a path between them. This is called average

connected distance in (Broder et. al, 2000). We

estimated this measure on UK-2002 and UK-2005

data sets through experiments. Table 1 shows the

estimated diameter of these data sets together with

the number of nodes and edges.

We use the resulted diameter to evaluate the

distances between our extracted bipartite cores.

3.3 Date Preparation

3.3.1 Pruning

Most of the links between pages in a site are for

navigational purposes. These links may distort the

result of presented algorithm. The result of the

HITS-Ranking algorithm on this un-pruned graph

will result in hub and authority pages to be found in

a site. To eliminate this effect we remove all links

between pages in the same site.

We assume pages with the same host-name are

in the same site. Table 2 shows the number of nodes

and edges after pruning in the UK data sets.

Table 1: UK 2002 and 2005 Data Sets information before

pruning.

Data Set Nodes Edges

Diameter

Estimate

UK-2002 18,520,486 298,113,762 14.9

UK-2005 39.459.935 936,364,282 15.7

Table 2: UK 2002 and 2005 Data Sets information after

pruning.

Data Set Nodes Edges

UK-2002 18,520,486 22,720,534

UK-2005 39.459.935 183,874,700

3.4 Results of Extracted Seeds

We run our algorithm for seeds extraction, Extract-

Seeds, on UK-2002 and UK-2005. This algorithm,

as Figure 3 shows, sets CoverDensity to 100 for

seeds extraction. Figure 4 shows the size of

extracted hubs and authorities in different iteration

from UK-2002. It is clear that these cores are

complete-bipartite. To reduce the impact of outlier

hub sizes in the graphical presentation, we have used

a log diagram. Figure 5 depicts the size of the

extracted hubs and authorities in different iterations

for UK-2005.

Normally, the hub sizes are bigger than the

authority sizes. We obtained bipartite cores with

very large hub sizes in UK-2002. So, we have

limited the number of hubs to 999 in UK-2002 data

set.

3.5 Quality Analysis

3.5.1 Metrics for Analysis

We used some different metrics to evaluate the

quality of extracted seeds. The first metric is the

distance between extracted seeds. As we have

WEBIST 2008 - International Conference on Web Information Systems and Technologies

102

mentioned earlier, a crawler tends to extract web

pages from different communities. Using HITS-

Ranking and Iterative pruning we can conclude that

extracted seeds are from different communities. To

prove this, we measure the distances between

extracted cores. We have defined core-distances as

the nearest directed path between one of the nodes in

the source core to one of the nodes in the destination

core.

0.5

1.5

2.5

3.5

1234567 8910

Hub Authority

Figure 4: Log diagram of Hub and Authority sizes

Extracted from UK 2002 in different iteration.

The second metric, is the PageRank of pages that

will be crawled starting from these seeds. If the

average PageRank of crawled pages, at each step of

crawl, is bigger than a random crawl, especially at

the beginning, then we can conclude that a crawl

that starts from those seeds identified by our

algorithm will result in better pages.

The third metric is the number of crawled pages

at each step of crawling. If the number of crawled

pages starting from extracted seeds by our method at

each step is bigger than the number of crawled pages

starting at random set, then we can conclude that our

method leads a crawl toward visiting more pages in

less iteration too.

For the first metric, we measure the distance

between the cores. For the other two metrics, we

need to crawl the graph starting from seeds extracted

with our method and compare it with a crawl starting

from randomly selected seeds.

3.5.2 Result of Bipartite Core Distances

We have measured the distance between all bipartite

cores that were extracted from UK datasets and they

had a reasonable distance in comparison with the

diameter of the related graph. Figure 7, shows the

graphical representation of distances between 56

cores extracted from UK-2002. The number on top

of each node indicates the iteration number in which

the core has been extracted. Because the distance

graph between nodes may have not an Euclidian

representation, distances in this figure do not exactly

match with real distances. The other important

information is that bipartite cores in close iterations

have a distance equal or bigger than average

distance of related web graph. The cores that are

close to each other are identified in far iteration. As

an example, the distance between core extracted

from iteration 32 and the core extracted from

iteration 47 is one. In this sample, the minimum

distance between nodes is 1, maximum distance is

13 and average distance is 7.15. As the diameter of

UK-2002 data set is 14.9, core distances are fine.

0.5

1.5

2.5

3.5

12345678910

Hub Authority

Figure 5: Log diagram of Hub and Authority sizes

Extracted from UK 2005 in different iteration.

Figure 6: Graphical representation of distances between 56

extracted seeds from UK-2002 by our algorithm. The

number on top of each node(core) indicates the iteration

number in which the related node has been extracted.

3.5.3 Average PageRank and Visit Count

In this section, we evaluate the second and third

metrics we defined for evaluation. For UK-2002 we

have executed the Extract-Seed algorithm with

SeedCount=10. Therefore, the algorithm extracts one

seed from each core in iteration. Then, we have

started a crawling on UK-2002 data set

implementing BFS strategy and measured the

average PageRank of visited pages in each crawl

depth, and the number of pages visited in each crawl

depth. Then, we have compared the results with

those gained from a crawl starting from random

seeds for the same graph.

A FAST COMMUNITY BASED ALGORITHM FOR GENERATING WEB CRAWLER SEEDS SET

103

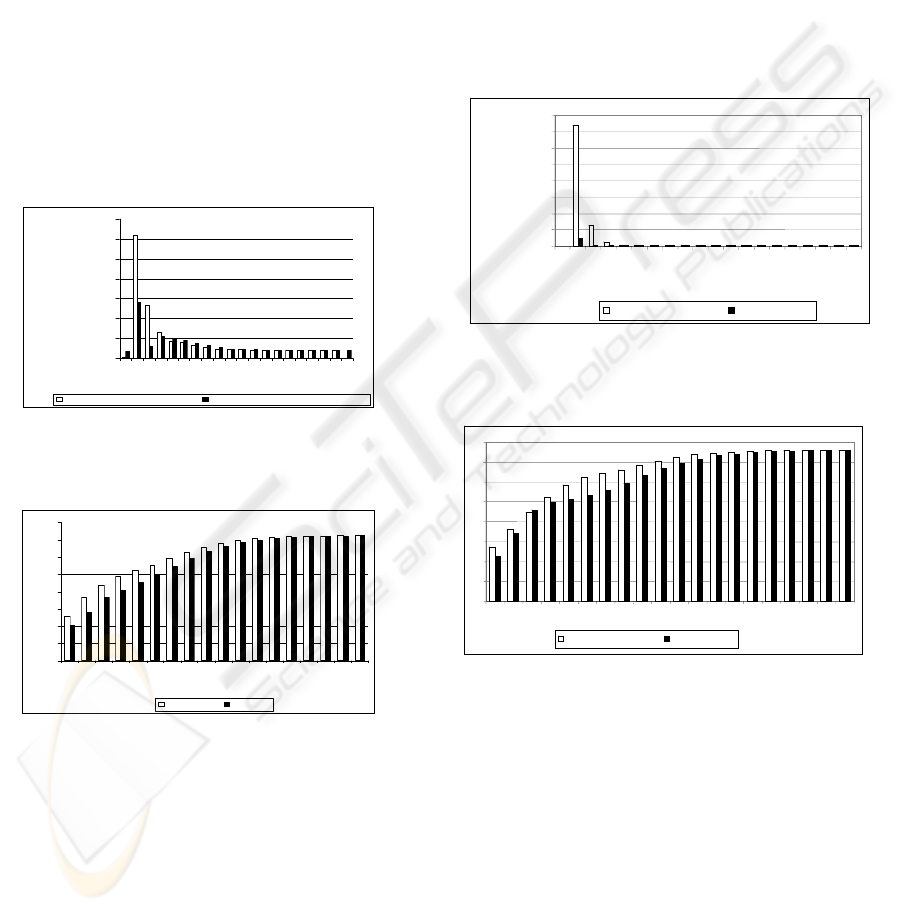
Figure 7 shows the comparison of average

PageRank of crawl starting from seeds extracted

with our method and a crawl starting from random

seeds. Except the first depth (iteration) of crawl, in

the other steps, up to step 4, the average PageRank

of pages crawled with our method appear to be

better. Specially, in the second and third iterations,

the difference is superior. In the later iterations

average PageRank of visited pages are close.

Figure 8 shows the comparison of log-number of

pages visited in each depth of crawl on UK-2002.

For better graphical representation, we have

computed log-count of visited pages. Apparently,

the results of our method are always better than

crawl starting random seeds and a crawl with seeds

extracted with our method downloads more pages in

less iteration. Figures 9 and 10 show the experiments

on UK-2005. The same results appear here too.

0.00E+00

5.00E-05

1.00E-04

1.50E-04

2.00E-04

2.50E-04

3.00E-04

3.50E-04

Iteration

PageRank

Our Algorithm Mean PageRank Random Algorithm Mean PageRank

Figure 7: Comparison between PageRank of Crawled

pages starting from 10 seeds extracted by our method on

UK-2002 and Random Seeds.

1 2 3 4 5 6 7 8 9 1011 12131415161718

Iteration

Log-Count Traversed pages

Our Method Random

Figure 8: Comparison between Log Count diagram of

pages visited at each Iteration starting from 10 seeds

extracted by our method and 10 seeds selected randomly

from UK-2002

3.5.4 Good Seeds for a New Crawl

Using proposed algorithm we have discovered seeds

from UK 2002 and UK 2005. Then we have

evaluated the utility of these seeds using three

evaluation criteria. These evaluations are good, but a

real crawler has not access to seeds of a web graph

which it is going to crawl. We should show that the

result is always good if we start the crawl using

seeds extracted from an old crawled graph.

In this section, we show the result of crawling on

UK 2005 using seeds extracted by our method and

compare it by randomly crawled seeds to simulate

the real environment. Before algorithm's execution,

we have checked the validity of seeds found from

UK-2002 in UK-2005 data set. If a seed does not

exist in the newer graph, then we remove that seed

from our seeds set. Our experiments show that only

11 percent of seeds exist in the new data set. In fact,

we have extracted 100 seeds from UK 2002 to be

sure that we have 11 valid seeds in UK 2005.

Figure 9: Comparison between PageRank of Crawled

pages starting 10 seeds extracted from UK-2005 by our

method and 10 Random seeds selected from UK-2005.

Figure 10: Comparison between Log Count Diagram of

pages visited at each Iteration starting from 10 seeds

extracted by our method from UK-2005 and 10 seeds

selected randomly on UK-2005.

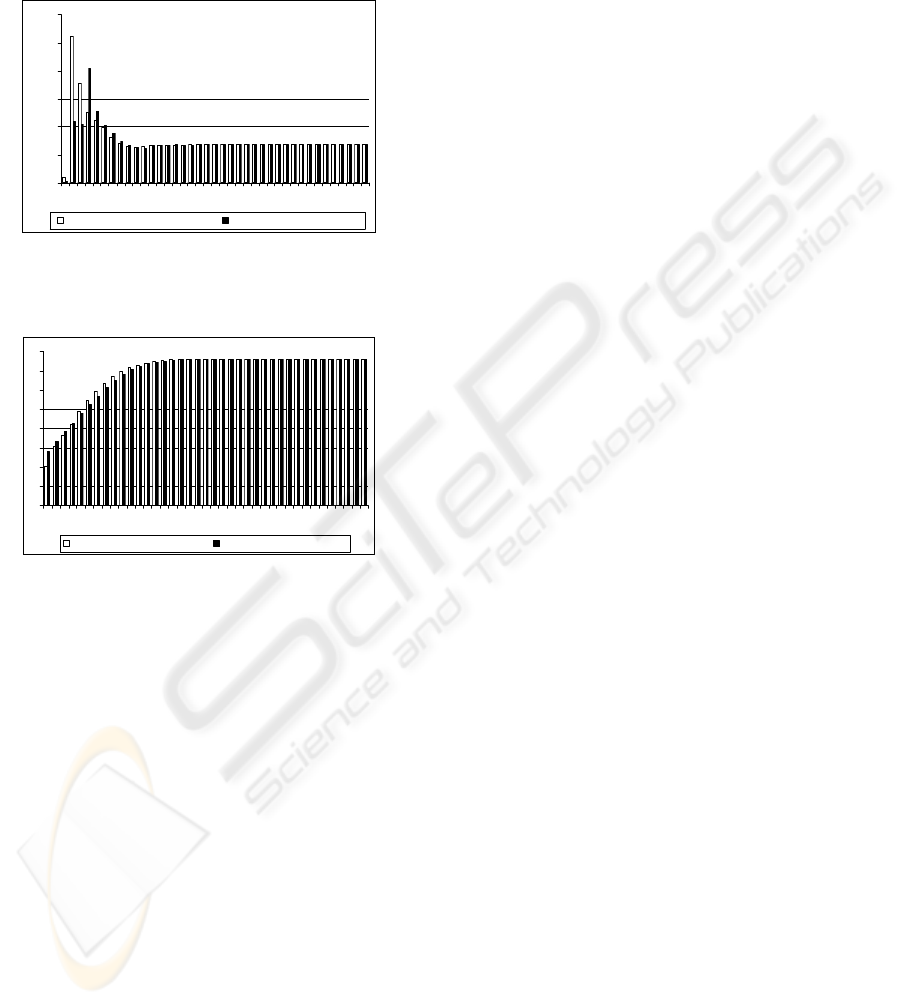
Figure 11, shows the comparison of average

PageRank of crawl starting from seeds extracted

with our method and a crawl starting from random

seeds. The result of our method is better until

iteration 3. Figure 12, shows the comparison of log-

number of pages visited in each depth of the crawl.

In this case, the result of our method is better than

the random case between steps 4 and 15. In fact, our

method download pages with high Page Rank till

iteration 3 and next it crawls more pages than the

134567 89

10 11 12 15 16

17 18 19 20

0.00E+00

2.00E-04

4.00E-04

6.00E-04

8.00E-04

1.00E-03

1.20E-03

1.40E-03

1.60E-03

123 4 5 6 7 8 9

10 11 12 13 14 15 16 17 18 19 20

Iteration

Our Method-Seed 2005

PageRank

Random Seeds

Our Method-Seed 200

Random Seeds

WEBIST 2008 - International Conference on Web Information Systems and Technologies

104

random case till iteration 15. After that, the result is

nearly the same. Therefore, we can conclude that a

crawler can download qualified web pages in less

iteration; starting generated seeds set using our

algorithm in less iteration.

0.00

5.00

10.00

15.00

20.00

25.00

30.00

1 3 5 7 9 111315171921232527293133353739

Our Method Seeds from UK 2002 Random Seeds from UK 2005

Figure 11: Comparison between PageRank of Crawled

pages starting 11 seeds extracted from UK-2002 by our

method and 11 Random seeds selected from UK-2005.

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39

Our Method Seeds from UK2002 Random Seeds from UK2005

Figure 12: Comparison between Log Count Diagram of

pages visited at each Iteration starting from 11 seeds

extracted by our method from UK-2002 and 11 seeds

selected randomly on UK-2005.

4 CONCLUSIONS

Crawlers like to download more good pages in less

iteration. In this paper, we have presented a new fast

algorithm with running time O(n) for extracting

seeds set from previously crawled web pages. In our

experiments we have showed that if a crawler starts

crawling from seeds set identified by our method,

then it will crawl more pages with higher PageRank

in less iteration and from different communities,

than starting a random seeds set. In addition, we

have measured the distance between selected seeds

to be sure that our seeds set contains nodes from

different communities. According to our knowledge,

this is the first seeds extraction algorithm that is able

to identify and extract seeds from different

communities.

Our experiments were on graphs containing at

most 39M nodes and 183M edges. This method can

be experienced on larger graph in order to

investigate the resulting quality on them too.

Another aspect where improvement may be

possible is the implementation of the seeds that are

not found in a new crawl. In our experiments, we

have simply ignored nodes present in an older graph

but not in the newer one. This aspect may be

improved by finding similar nodes in the newer

graph.

ACKNOWLEDGEMENTS

Authors would like to thank Mohammad Mahdian

for his helpful and valuable comments on earlier

draft of this work.

REFERENCES

Henzinger, M. R., 2003. Algorithmic challenges in Web

Search Engines. Internet Mathematics, vol. 1, no. 1,

pp. 115-123.

Cho, J. Garcia-Molina, H. and Page, L., 1998. Efficient

Crawling through URL ordering. In Proceedings of

the 7th International World Wide Web Conference,

April, pp.161-172.

Najork, Wiener, J. L., 2001. Breadth-First Search

Crawling Yields High-Quality Pages, Proceedings of

the 10th international conference on World Wide

Web,pp. 114-118.

Brin, S. and Page, L., 1998. The anatomy of a large-scale

hypertextual Web search engine. Proceedings of the

seventh international conference on World Wide Web

7, pp. 107 – 117.

Jon M. Kleinberg, J., 1999. Authoritative Sources in a

Hyperlinked Environment. Proc. 9th ACM-SIAM

Symposium on Discrete Algorithms, pp.604-632.

Laboratory for Web Algorithmics, [Online], Available:

http://law.dsi.unimi.it/ [19 Jan. 2007]

Boldi, P., and Vigna, S., 2004. The WebGraph framework

I: Compression techniques. In Proc. of the Thirteenth

International World Wide Web Conference, pp. 595-601.

Boldi, P., Codenotti, B., Santini, M., Vigna, S., 2004,

UbiCrawler: A Scalable Fully Distributed Web

Crawler, Journal of Software: Practice & Experience,

vol.34, no 8, pp. 711-726.

Albert, R. Jeong, H. Barabasi, A. L., 2000, 'A random

Graph Model for massive graphs', ACM symposium on

the Theory and computing.

Andrei Z. Broder, Ravi Kumar, Farzin Maghoul,

Prabhakar Raghavan, Sridhar Rajagopalan, Raymie

Stata, Andrew Tomkins, Janet L. Wiener, 2000. Graph

structure in the Web. Computer Networks, pp. 309-320.

A FAST COMMUNITY BASED ALGORITHM FOR GENERATING WEB CRAWLER SEEDS SET

105