PROCESSING AND MANAGING COMPLEX OWL DATA
Hussam Abuazab
1
and Atilla Elci
Department of Computer Engineering, Eastern Mediterranean University, Gazimagusa, North Cyprus, Turkey
1
Al Ghurair University, Dubai, U.A.E.
Keywords: OWL class sets, DeMorgan’s Law, minusOf, Auxiliary identity.
Abstract: In this paper we introduce new OWL class sets that can be obtained through and manipulated by Boolean
operators. The need for new class sets come in order to process and manage complex OWL data, and to
improve the expressive power of OWL language. A particular need for such sets arises in processing
complex data involved in ontology for human disease which is being developed. The class sets introduced in
this paper include the definition of minusOf, De Morgan's Law, and Auxiliary Identity properties.
1 INTRODUCTION
OWL is rich with constructs in class expression
category like owl:oneOf, owl:disjointWith,
owl:unionOf, owl:complementOf; and in Enumerated
values like owl:dataRange. Also, Boolean class
combinations extended to include owl:intersectOf,
which play major role in representing intricacies in
ontology (Bennacer, 2004). Yet, ontology of
diseases (Ashburner, 2000) give way to complex
data and combinations there of which is very
cumbersome to represent using the existing class
definitions and operators, which result on poor
representations of the ontology. Although there are
several reasons for poor ontology described on
(Hepp, 2006), lack of some class set definition is a
reason for this problem. The new class set will help
on minimize the gap between conceptual data
schemes and ontologies, which rise as hot topic on
the march of developing tools for building strong
ontologies (Jarrar, 2003).
In the following section, we introduce new class sets
to use in representing complex data of ontology of
diseases. Section 3 discusses the use of these new
sets in diagnosing in the presence of symptoms of
multiple ailments. Section 4 concludes the paper.
2 COMPLEX CLASS SETS
In this section we introduce three new OWL class
selectors and their resultant class sets, namely,
minusOf, De Morgan's Law, and Auxiliary
Identity.
2.1 minusOf Class
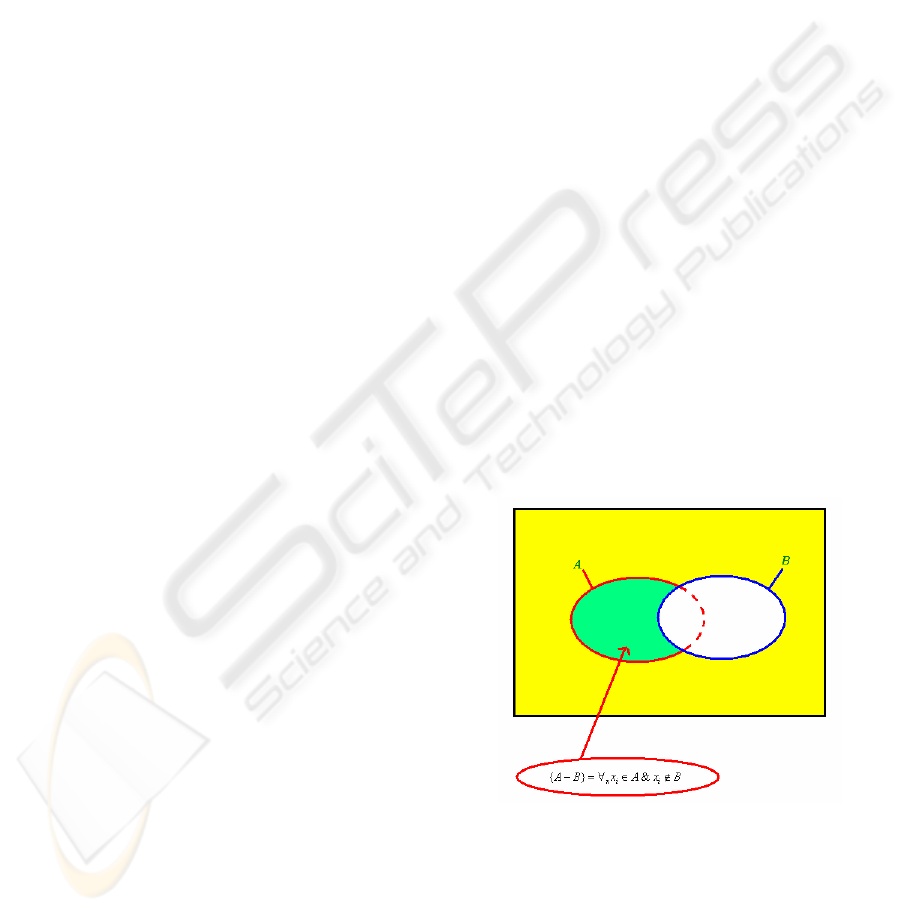
The minusOf represents the set
BxAxBA
iix
∉
∈
∀
=
−
&}{ where A & B are
OWL class sets, for example symptoms of two
diseases.
Figure 1: The class of minusOf.
A: symptoms of Disease A.
B: symptoms of Disease B.
So, minusOf (A,B) represents the symptoms of
disease A excluding those shared with the symptoms
of disease B.
237
Abuazab H. and Elci A. (2008).
PROCESSING AND MANAGING COMPLEX OWL DATA.
In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 237-240
DOI: 10.5220/0001528402370240
Copyright
c
SciTePress

2.2 DeMorgan's Law Class
De Morgan's Law class represents the
CBA ∩∩ =
___
CBA ∪∪ , which implies that the
intersect elements are not satisfied. Let’s assume
that A, B, and C are classes of symptoms of three
different diseases, and then
CBA ∩∩ implies that
the common symptoms are not satisfied.
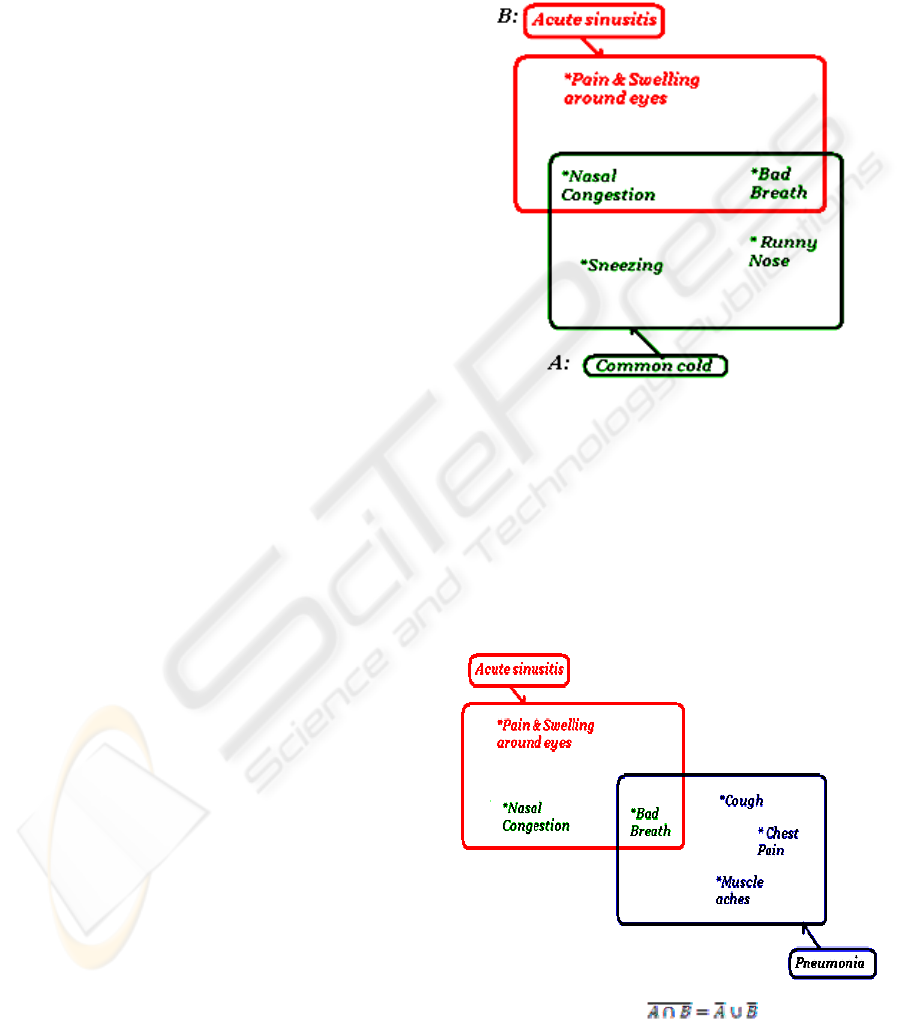
In the way of an example let’s consider the
following OWL description of three diseases on
figure 2, for example, acute sinusitis, pneumonia and
common cold. Each disease has known symptoms,
and some symptoms may be common among all or
between any two diseases.
Figure 2: OWL description of three diseases.
Figure 2 (cont): OWL description of three diseases.
Studying the above OWL description, it is clear that
there are some common symptoms between the three
diseases. Figure 3 shows the intersections between
the three classes of symptoms of the three diseases.
Figure 3: Class of De Morgan's Law.
Bad Breath is the common symptom among the
three diseases. The patient must suffer from bad
breath so he/she may be said to have been infected
by at least one or more of the three diseases, acute
sinusitis, and pneumonia and common cold. In case
the patient is not suffering from bad breath, this
implies that he/she must not have been infected by
any of the three diseases.
This can be represented by De Morgan's Law as
following:
CBA ∩∩ =
___
CBA ∪∪
where A is for symptoms of acute sinusitis, B is for
pneumonia, and C is for common cold.
WEBIST 2008 - International Conference on Web Information Systems and Technologies
238
So instead of calculating the values of
_
A
,
_
B , and
_
C , and then finding the union of these classes,
applying De Morgan's Law, will result in
professional solution in means of time and
complexity.
2.3 Auxiliary Classes
Auxiliary Classes represent the sets:
1.
A
A
B
A
=+
By supposing A: symptoms of Disease A, and B:
symptoms of Disease B, the set
AABA
=
+
implies that the patient suffers from symptoms of
disease A, and the shared symptoms of diseases A
and B, so the patient infected by disease A.
2.
B
A
B
AA +=+
−
In this case, the patient suffers from symptoms of
disease A, and symptoms of disease B, except the
ones common with disease A, so the patient effected
by disease A and B.
3.
BCACABA
+
=++ ))((
In this case, the patient suffers from symptoms of
disease A, and symptoms of disease B, so, let us say,
the patient suffers from sneezing – symptom of
common cold – and from pain and swelling around
eyes – symptom of Acute Sinusitis – also, the patient
suffering from chest pain - symptom of Pneumonia –
so, for sure, the patient is suffering from bad breath
which is the intersect symptom of both Acute
Sinusitis and Pneumonia. See Fig. 2.
3 DISCUSSION
The mentioned three complex classes are comply to
the standards of OWL classes regarding the name
(URIref) with the “rdf:ID” attribute; also, the class
may have properties and instances. The tag for
defining the new classes is OWL:Class.
The
minusOf class is used to implement the cases
where the shared symptoms of two diseases are not
available while the non-shared symptoms of one
disease are available; let us assume a patient is
suffering from sneezing, which may imply that
he/she is infected by common cold, but the patient is
neither suffering from nasal congestion nor bad
breath, which implies the patient is not infected by
acute sinusitis for sure, as A-B is true for the patient.
So the symptoms of pain and swelling around eyes
need not be investigated, and the result is diagnosed
more precisely and in lesser time. Reference Figure
4.
Figure 4: minusOf Class.
The De Morgan's class is used to simplify the
diagnosing path, for example, if the patient is not
suffering from bad breath then he/she is not infected
by either of common cold, acute sinusitis, or
pneumonia. This also indicates that one of the other
non-common symptoms may be investigated to
determine which ailment is present. Reference
Figure 5.
Figure 5: .
The minusOf Class may have the property
hisExcludedInstance to represent the instances of
PROCESSING AND MANAGING COMPLEX OWL DATA
239

class A which are shared with class B. The
DeMorgan'sLaw Class may have the property
nonCommonInstance to represent the complement of
the common instances between the input classes.
Of the
Auxiliary Classes, the first class
A
A
B
A
=+ , if the patient is suffering from
sneezing – symptom of common cold – and from
nasal congestion – symptom of both common cold
and acute sinusitis – then the patient is infected by
common cold for sure, while more investigations are
required to decide whether he/she infected by acute
sinusitis as well. The second class of the Auxiliary
Classes
,
B
A
B
AA
+
=+
−
, states that if the
patient is suffering from sneezing – symptom of
common cold – and from pain and swelling around
eyes – symptom of acute sinusitis but not of
common cold – then the patient is infected either by
common cold or acute sinusitis or both diseases.
The third
Auxiliary Class,
BCACABA +=++ ))((
, indicates that if the
patient is suffering from common cold – disease A –
and sometimes suffering from acute sinusitis or
pneumonia, so the patient for sure suffering from
bad breath.
4 CONCLUSIONS
In this paper, we introduced new ontology classes.
The minusOf class is used for example to represent
the symptoms of a disease except those shared with
some other disease which implies that the patient is
infected by one but not the other disease. The
DeMorgan’s Law class is utilized to check the
availability and non-availability of common
symptoms of more than one disease, which implies
that the patient is not infected by all diseases causing
the shared non-available symptoms. Finally, three
auxiliary classes are defined to represent various
symptoms’ availability.
The
minusOf and DeMorgan's Law classes
introduced in this paper will play prime role on
easing the representation of complex knowledge,
especially medical knowledge, and the knowledge
that requires such sort of complex classes. The three
auxiliary classes defined are meant to ease the
querying process by deducing the common instances
and individuals of different classes.
In the future more of such specialized classes may
be introduced in order to enhance OWL’s level to
represent more complex knowledge. Also, similarity
may be drawn with implementing combination of
logic gates that subsume certain knowledge,
consequently easing the processing of related data
sets.
REFERENCES
Bennacer, N. Bourda, Y. Doan, B. "Formalizing for
querying learning objects using OWL", Supelec,
France Sept. 2004; ISBN: 0-7695-2181-9
M. Ashburner, C. A. Ball, J. A. Blake, D. Botstein, H.
Butler, J. M. Cherry, A. P.Davis, K. Dolinski, S. S.
Dwight, J. T. Eppig, M. A. Harris, D. P. Hill, L. Issel-
Tarver, A. Kasarskis, S. Lewis, J. C. Matese, J. E.
Richardson, M. Ringwald, G. M.Rubin, and G.
Sherlock. Gene ontology: tool for the unification of
biology. the gene ontology consortium. Nat Genet,
25(1):25–9, 2000. 1061-4036 Journal Article.
Martin Hepp, Jos de Bruijn GenTax: A Generic
Methodology for Deriving OWL and RDF-S
Ontologies from Hierarchical Classifications,Thesauri,
and Inconsistent Taxonomies Int’l Journal on
Semantic Web and Information Systems (IJSWIS), ,
pp. (2006b)
Jarrar, M., Demey, J., Meersman, R.: On Using
Conceptual Data Modeling for Ontology Engineering.
In Spaccapietra, S., March, S., Aberer, K., (Eds.):
Journal on Data Semantics (Special issue on Best
papers from the ER, ODBASE, and COOPIS 2002
Conferences). LNCS, Vol. 2800, Springer, pp.:185-
207. October 2003.
WEBIST 2008 - International Conference on Web Information Systems and Technologies
240
