
WORKFLOW TREES FOR REPRESENTATION AND MINING OF
IMPLICITLY CONCURRENT BUSINESS PROCESSES
Daniel Nikovski
Mitsubishi Electric Research Laboratories, 201 Broadway, Cambridge, U.S.A.
Keywords:
Business process management, Process mining, Petri nets.
Abstract:
We propose a novel representation of business processes called workflow trees that facilitates the mining of
process models where the parallel execution of two or more sub-processes has not been recorded explicitly in
workflow logs. Based on the provable property of workflow trees that a pair of tasks are siblings in the tree
if and only if they have identical respective workflow-log relations with each and every remaining third task
in the process, we describe an efficient business process mining algorithm of complexity only cubic in the
number of process tasks, and analyze the class of processes that can be identified and reconstructed by it.
1 INTRODUCTION
The organization and optimization of business pro-
cesses within an enterprise is essential to the success
of that enterprise in the marketplace, and the explicit
management of business processes within dedicated
software suites has emerged as an important class of
information technology (van der Aalst and van Hee,
2002). Key to the successful management of business
processes is the nature of the models used for pro-
cess representation, construction, maintenance, and
improvement. Whereas some kind of graphical repre-
sentation has been used almost universally, the types
of proposed models and the semantics associated with
them have varied widely. Some of the more popu-
lar representations include Petri nets (van der Aalst
et al., 2004), finite state machines and Markov models
(Cook and Wolf, 1998a), as well as special-purpose
graphic formalisms such as AND/OR trees (Silva
et al., 2005) and block diagrams (Schimm, 2004). In
most cases, these graphic representations are also as-
sociated with a corresponding formal language that is
interpretable by BPM sequencing middleware. For an
extensive comparison between business process mod-
eling formalisms from several perspectives, see, for
example (List and Korherr, 2006).
The abundance of modeling formalisms suggests
that there isn’t a single best representation, but rather,
multiple trade-offs exist when adapting formalisms to
a particular task, and the wide choice of available for-
malisms is in fact beneficial. The specific task of in-
terest addressed in this paper is the learning from data
of representations for processes with implicit concur-
rency. We propose a solution to this problem in the
form of a novel representation for business processes,
and an associated algorithm for mining such mod-
els from data with very favorable computational com-
plexity (cubic in the number of process tasks).
2 PROCESS MINING AND
IMPLICIT CONCURRENCY
The objective of process mining algorithms and sys-
tems is to construct an explicit process model from
recorded event logs (van der Aalst and Weijters,
2004). This functionality is especially useful when
a new business process management (BPM) system
is deployed at a customer site and explicit models
of the existing processes have to be produced as a
starting point for analysis, process re-engineering,
etc. The traditional alternative to process mining
— the manual construction of process models, usu-
ally using graphic editors — can be very time- and
labor-intensive, because it typically involves inter-
views with executives, and also very imprecise, be-
cause humans can only describe the way they imag-
ine business processes operate, and not the way these
business processes actually operate. At the same time,
if the business processes already involve information
technology (e.g. enterprise resource planning sys-
30
Nikovski D. (2008).
WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS PROCESSES.
In Proceedings of the Tenth International Conference on Enterpr ise Information Systems - ISAS, pages 30-36
DOI: 10.5220/0001671900300036
Copyright
c
SciTePress

tems, customer relationship management systems), in
all likeliness, abundant execution logs from these sys-
tems already exist. In such cases, using these execu-
tion logs to automatically extract process models can
result in major savings in time and effort and improve
model accuracy significantly.
The objective of process mining is to find a model
of a business process (represented in a suitable for-
malism) solely by inspecting the relative order of
tasks as manifested in logs collected from the re-
peated execution of the business process. It is as-
sumed that N different tasks t
i
, i = 1, N, t
i
∈ T from
the set T can be distinguished in the execution log.
The workflow logs are divided into disjoint episodes
that correspond to the processing of one work case
each. During one episode, the case takes one possible
path through the process. An episode is represented
as a sequence of tasks, and indicates the sequential
order in which a particular case was processed. The
objective of process mining algorithms, then, is to in-
spect the entire workflow log and induce a process
model that could have produced this log. It is usu-
ally desired that the induced model be as compact as
possible, and have no duplicate tasks.
Initial research recognized that process mining is
a special case of inductive machine learning (ML),
hence generic ML techniques, most commonly based
on heuristic search, are applicable to this problem.
Early examples of this approach included the algo-
rithms of Cook and Wolf (Cook and Wolf, 1998a;
Cook and Wolf, 1998b), which employed greedy in-
duction over model spaces representing Markov mod-
els and Petri nets. While successful, the heuristic na-
ture of search in model spaces does not guarantee the
discovery of the optimal model, where optimality is
usually defined as a trade-off between model accuracy
and parsimony. Further complicating the problem of
finding the optimal model is the issue of data suffi-
ciency — certainly, if the exact relationship among
tasks is not manifested in the execution logs, a correct
(and much less, optimal) model cannot be mined from
these logs.
A major shift from heuristic search and inductive
methods occurred with the emergence of constructive
algorithms, such as α, α+, and β (van der Aalst et al.,
2004; de Medeiros et al., 2004). These algorithms
pre-compute the relations between each pair of tasks
as manifested in the execution log and organize the
identified relations in a tabular format. After that, the
algorithms construct a model based on this relations
table only, without having to examine the execution
log ever again.
Perhaps the best known example of this class of
constructive algorithms is the α algorithm proposed
by van der Aalst et al., 2004. The business process
representation used by this algorithm is structured
workflow nets (SWF-nets) — a carefully chosen and
precisely defined subset of Petri nets that avoids unde-
sirable situations such as deadlocks, incomplete tasks,
indeterminate synchronization, etc.
A significant novel idea of the α algorithm is to
pre-process the execution log and determine the pair-
wise relations between all pairs of tasks. These so
called log-based ordering relations between a pair of
tasks a and b are as follows:
• a > b iff there exists at least one episode of the log
where a is encountered immediately before b,
• a → b iff a > b and b 6 >a,
• a#b iff a 6 >b and b 6 >a, and
• a k b iff a > b and b > a.
The assumption of these algorithms is that the sup-
plied workflow log is complete, i.e. it reflects cor-
rectly the relations between the tasks in the real pro-
cess that produced the log. This assumption is rea-
sonable for most execution logs collected from real
enterprise information systems. Once the relation be-
tween each pair of tasks has been identified to be one
of these four relations, the algorithm proceeds to con-
struct a minimal SWF-net that satisfies the relations.
Based on the provable property that a → b implies that
a SWF-net place exists immediately between tasks a
and b, van der Aalst et al., 2004 devised an algorithm
that builds an SWF-net in eight steps, without any
heuristic search.
The α algorithm is able to mine a large class
of SWF-nets. However, one important limitation of
the α algorithm and its derivatives is that they can-
not detect all cases of concurrency in a business pro-
cess. Concurrent tasks in SWF-nets are represented
by means of a construct involving auxiliary AND-
split and AND-join tasks (cf. Fig. 1). We will refer
to this construct as an AND-block. If we compare it
to the case of task choice (exclusive OR, or an OR-
block), where only one of several tasks is executed,
it is evident that an OR-block involves no such aux-
iliary tasks (cf. Fig. 2). The α algorithm can mine
processes with AND-blocks as long as the two aux-
iliary tasks, the AND-split and the AND-join, have
been recorded explicitly in the workflow log. We will
call such processes explicitly concurrent, i.e., when
concurrency is present, the initiation and completion
of parallel execution is explicit in the log.
However, it cannot be expected that workflow logs
would contain explicit AND-splits and AND-joins,
because they do not correspond to actual tasks in the
problem domain — whenever parallel execution has
WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS
PROCESSES
31

&-s
A
B
&-j
Figure 1: A WF-net for representing parallel execution:
tasks A and B are executed concurrently. Here the tasks
labeled &-s and &-j are auxiliary and have the sole purpose
of explicitly specifying concurrency.
A
B
Figure 2: A WF-net for representing exclusive choice: ei-
ther task A or task B is executed, but not both.
been performed in a given legacy IT system, the de-
cision to initiate it and the logic to synchronize its
completion is usually buried somewhere deep into ex-
ecutable code, and it is precisely the objective of the
process mining algorithm to extract it and model it
explicitly.
When explicit AND-splits and AND-joins are ab-
sent from the workflow file (which we expect to be the
typical situation), the mining algorithm would have to
deal with implicitly concurrent business processes. In
numerous cases, the α algorithm and its descendants
would have difficulties in handling implicit concur-
rency. One specific instantiation of this problem is
when an AND-block is nested within an OR-block.
For example, van der Aalst, 2004 discussed the pro-
cess in Fig. 3, and concluded that if the synchroniz-
ing AND-split and AND-join tasks were not present
in the workflow log, the exact workflow net could not
be recovered by the α algorithm.
The reason why implicit concurrency is challeng-
ing for the α algorithm and its descendants is that
they never create new tasks other than those already
present in the workflow log, and hence cannot create
the explicit AND-blocks necessary to represent con-
currency in the SWF net formalism. This suggests
that perhaps it would be worthwhile to explore alter-
native representations and mining algorithms that can
&-s
B
C
&-j
E
D
A
Figure 3: This WF-net that cannot be recovered by the α
algorithm, if the auxiliary tasks &-s and &-j are missing
from the workflow log.
handle implicit concurrency better, while still aiming
at constructive solutions that build compact relation
tables from workflow logs. Another desirable prop-
erty of such algorithms would be more favorable com-
putational complexity — the run time of the α algo-
rithm and its derivatives is exponential in the number
of tasks N, since they involve search within the space
of all pairs of sets of tasks, i.e. the powerset of the
set of all tasks. For practical purposes, a mining algo-
rithm of low-degree polynomial complexity would be
much more desirable.
3 WORKFLOW TREES FOR
REPRESENTATION OF
BUSINESS PROCESSES
We propose a representation of business processes
that is based on the natural hierarchical organization
of work in most enterprises. The representation is
in the form of an ordered tree, where the leaves of
the tree represent tasks, and the internal nodes of the
tree represent the functional blocks in which these
tasks are organized. This representation is similar to
the block representation used by Schimm (Schimm,
2004) and the AND-OR graphs proposed by Silva et
al. (Silva et al., 2005) in the type of the blocks used.
Based on its hierarchical organization, it is also close
to the way sub-diagrams can be defined in UML 2.0
Activity Diagrams.
In this paper, we will consider trees that have four
building blocks, labeled as follows: parallel (AND),
choice (OR), sequence (SEQ), and iteration (ITER).
The meaning of the AND and OR blocks is as shown
in Figs. 1 and 2, in Petri net notation. The meaning
of the SEQ construct is obvious, and is shown in Fig.
4. For the iteration construct, two definitions are pos-
sible, depending on whether zero executions of a task
are allowed, or it has to be executed at least once. The
two alternative definitions are shown in Fig. 5.
These constructs are very similar to those used in
van der Aalst and van Hee, 2002 (with the exception
of the iteration construct, which must involve at least
two tasks there). It has been shown that by starting
with one of these constructs, and recursively substi-
tuting its component tasks with compound blocks of
more tasks, a large class of sound and safe nets can be
constructed. Our proposal for workflow trees formal-
izes this intuition: the structure of the tree prescribes
the steps that must be taken during this process of top-
down recursive construction of a business process. It
also describes a way to convert a workflow tree (WF-
tree) into a SWF-net: by traversing the WF-tree in
ICEIS 2008 - International Conference on Enterprise Information Systems
32
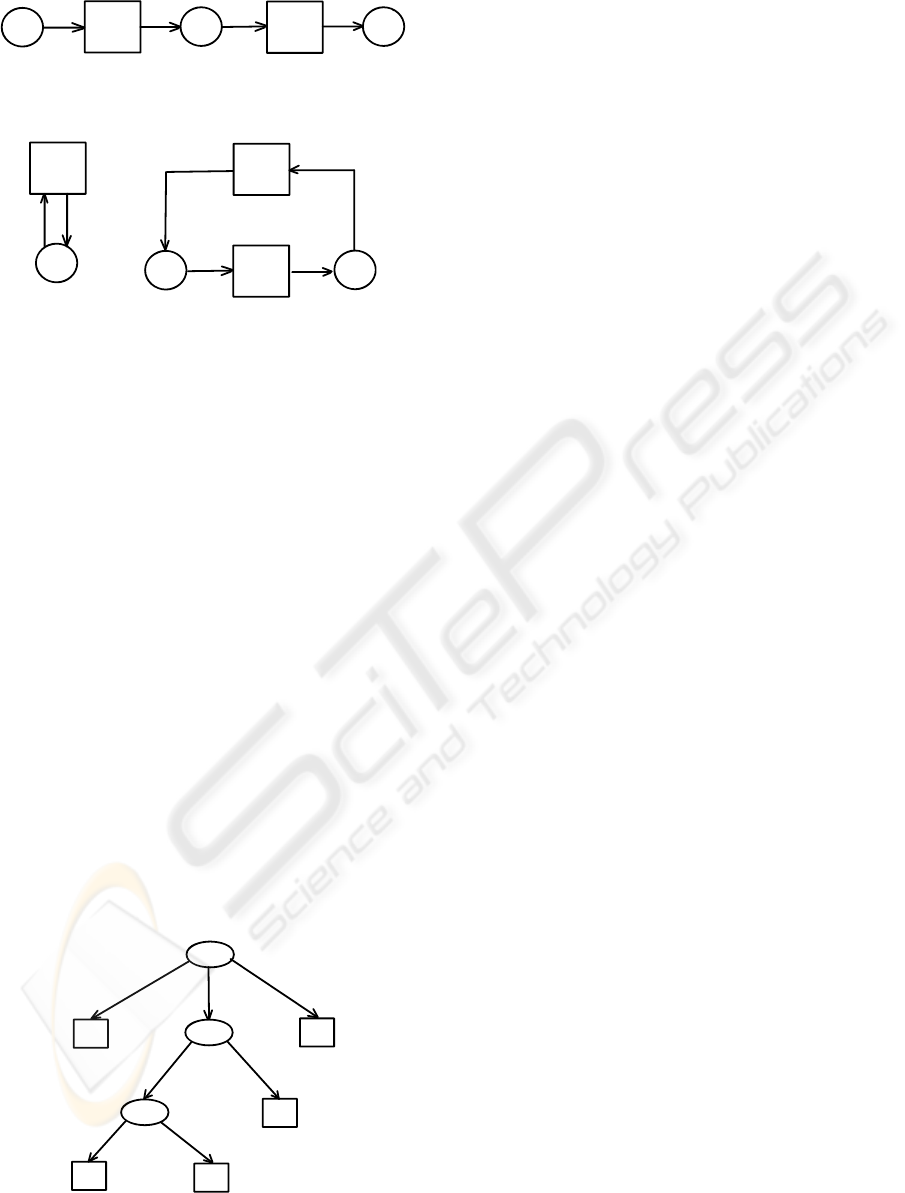
A
B
Figure 4: A WF-net that specifies sequential execution:
tasks A and B are always executed strictly in this order.
A
B
Figure 5: Two possible WF-nets that specify iterative exe-
cution. The net on the left allows zero or more executions
of task A, while the net on the right specifies that task B
should be executed at least once (and possibly many more
times).
any convenient order, each tree node is replaced by
its corresponding Petri net, as described above, and if
any of the children of this node are nodes themselves,
the procedure is recursively repeated until all tasks in
the resulting SWF-net are atomic tasks. As an exam-
ple, Fig. 6 shows the WF-tree that would result in the
SWF-net previously shown in Fig. 3, if expanded as
described.
While this general approach to constructing busi-
ness process models is intuitive and has been explored
before, the specific representation in a tree-like form
that we propose allows us to analyze and identify the
properties of this representation that are useful for the
purposes of process mining. In particular, we are in-
terested in the relations between pairs of tasks that are
entailed by this representation. We define a set of re-
lations AND, OR, SEQ, and IT ER that are n-ary, and
can hold between two or more tasks. Two tasks in
the WF tree have one of these relations between each
other. (In this case, the relation is binary.) We specify
A
D
B
C
E
SEQ
OR
AND
Figure 6: A workflow tree that corresponds to the WF-net
from Fig. 3.
that the binary relation between a pair of tasks in a
WF-tree is determined by the node of the tree that is
the least common ancestor (LCA) of these two tasks.
For example, for the SWF-net in Fig. 3 (respectively,
the tree in Fig. 6), the tasks A and E are in the SEQ
relation, and B and E are in the OR relation.
In the general case, it would be possible to have
process models with nested blocks of the same type,
for example an OR block nested immediately within
another OR block. In the corresponding WF-tree, this
would be expressed as one OR node having as a child
(direct descendant) another OR node. While certainly
possible and valid, such WF-trees are redundant, and
it is usually desirable to eliminate this redundancy.
We define a compact workflow tree (CWF-tree) to be
a workflow tree where no two nodes of the same label
have a direct parent/child relationship.
Before analyzing the properties of the described
relations, we will note that as a corollary of this spec-
ification and the nature of our specific definition of an
iterative block, no two tasks can be in the IT ER re-
lation. This is due to the fact that a tree node labeled
with ITER always has only one child, and hence can-
not be the LCA of any pair of distinct tasks. (This
is true regardless of which alternative definition of an
ITER block is chosen from the two shown in Fig. 5).
The remaining three relations have the following
properties. When these relations are binary, the binary
AND and OR are transitive and symmetric, while the
binary SEQ is transitive and asymmetric ((aSEQb) ⇒
¬(bSEQa)). Ternary relations can be defined by
aRb ∧ bRc ⇒ R(a, b, c), whereas relations of arbi-
trary arity have the property that R(a
1
, a
2
, . . . , a
n−1
) ∧
a
n−1
Ra
n
⇒ R(a
1
, a
2
, . . . , a
n−1
, a
n
). Here R can be any
of the three relations AND, OR, and SEQ. Note that
in combination with the asymmetry of the binary SEQ
relation, the n-ary SEQ relation is guaranteed to hold
only between arguments in the correct order, while the
symmetry of the binary AND and OR ensure that their
n-ary counterparts hold for an arbitrary order of their
arguments. For the sake of analytical convenience, we
will also define the symmetric relation LIN, such that
aLINb iff aSEQb∨bSEQa. The meaning of this rela-
tion is linear order — it holds true between two tasks
when one of them follows the other.
Note also that if three or more tasks are in the
same relation, it is not necessarily true that each pair
of them has the same LCA — since more than one
tree node can be labeled with the same block label,
it is completely possible that three or more tasks are
in the same relation, but are not descendants of three
different children of the same node.
What is true, though, is that any three tasks a,
b, and c of the same WF-tree can have at most two
WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS
PROCESSES
33

distinct relations R
1
, R
2
from the set {AND, OR, LIN}
among them.
Lemma 1. aR
1
b ∧ bR
2
c ⇒ aR
1
c ∨ aR
2
c, for R
1
, R
2
∈
{AND, OR, LIN}.
Proof. For full proof, see the accompanying online
technical report (Nikovski and Baba, 2007).
Furthermore, due to the symmetry of the three re-
lations AND, OR, and LIN, the lemma holds for all
possible symmetric exchanges in the order of tasks in
these relations. A direct corollary of this lemma (in
one respective instantiation as regards relation sym-
metry) is that if two tasks a and b are in relation R
1
(aR
1
b), and one of them (a) is in relation R
2
with
some third task c (aR
2
c), there are only two possi-
bilities for the relation between b and c: it is either
bR
1
c or bR
2
c. The former case (bR
1
c) holds when the
LCA of a and b is a descendant of the LCA of a and
c, while the latter case (bR
2
c) holds when the LCA of
a and c is a descendant of the LCA of a and b.
The latter case is of particular interest, and it is
true that the logical implication in question holds in
the other direction, too, even regardless of the exact
relation between a and b. By defining LCA(·, ·) to be
the function that returns the node of a WF-tree that
is the LCA of its two arguments, and the binary re-
lation Descendant such that Descendant(d, a) holds
true when node d is a descendant of node a, we can
show that if nodes a and b happen to share the same
relation R respectively with a third task c, it is nec-
essarily true that their LCA is a descendant of their
respective LCAs with this third task:
Lemma 2. aR
1
b ∧ aR
2
c ∧ bR
2
c ∧ R
1
6≡ R
2
⇒
Descendant[LCA(a, b), LCA(a, c)].
Proof. For full proof, see the accompanying online
technical report (Nikovski and Baba, 2007).
The same stipulation about the validity of this
lemma with respect to the symmetry of R
1
and R
2
ap-
plies here, too. It follows immediately that LCA(a, b)
is a descendant of LCA(b, c), as well. We can also
prove that LCA(a, c) ≡ LCA(b, c):
Lemma 3. (aR
1
b ∧ aR
2
c ∧ bR
2
c ∧ R
1
6≡ R
2
) ⇒
(LCA(a, c) ≡ LCA(b, c)).
Proof. Since both LCA(a, c) and LCA(b, c) are ances-
tors to LCA(a, b) by virtue of Lemma 2, and three
leaves in the same tree can have at most two distinct
LCA nodes, then they must be the same node, i.e.
LCA(a, c) ≡ LCA(b, c).
Also note that the condition that exactly two rela-
tions hold among the three tasks in Lemmata 2 and 3
is essential: if it is the same (one) relation that holds
between each pair of tasks, nothing can be said about
the relative position in the tree or number of their re-
spective LCA nodes.
Now we are prepared to analyze the relations be-
tween a pair of tasks and all other tasks, and prove
that two tasks are children (direct descendants) of the
same node iff they are in the same respective relation
with all other tasks. This property holds for com-
pact workflow trees that do not contain redundant par-
ent/child nodes of the same label, and also do not con-
tain intermediate nodes of type IT ER.
Theorem 1. (∀
c
∃
R
aRc ∧ bRc) ⇔ [∃
L
Child(a, L) ∧
Child(b, L)].
Proof. For full proof, see the accompanying online
technical report (Nikovski and Baba, 2007).
This theorem shows that we can identify tasks that
must have the same parent node in the CWF-tree by
comparing their respective relations with every other
task — if they all match, then the two tasks share the
same parent. We will use this theorem to devise a
computationally efficient process mining algorithm in
the next section. Note that the analysis will be limited
to CWF-trees without IT ER nodes, since the pres-
ence of such nodes makes impossible the application
of this theorem.
4 MINING OF WORKFLOW
TREES
In the previous section, we assumed that a CWF-tree
was given, and analyzed the properties of the rela-
tions among its tasks. In this section, we describe how
such a tree can be constructed, if all that is given is a
complete workflow log from the operation of the cor-
responding process. We will use a definition of log
completeness identical to that proposed by van der
Aalst et al., 2004.
Before we describe the algorithm for mining
workflow trees, we have to explain how all possible
pairwise relations between two tasks in a model are
determined. The binary relation AND is identical to
the relation k used in the α algorithm: aANDb ⇔
a k b. The relation SEQ is based on the relation
→ from that algorithm (a → b ⇒ aSEQb), but un-
like the latter, is transitive, and is more comprehen-
sive. From the above implication and the transitiv-
ity property aSEQb ∧ bSEQc ⇒ aSEQc, it follows
that aSEQb ∧ b → c ⇒ aSEQc, that is, the relation
SEQ is simply the transitive closure of →, and can be
found by any suitable algorithm, for example Floyd-
Warshall of complexity O(N
3
) (Sedgewick, 2002).
ICEIS 2008 - International Conference on Enterprise Information Systems
34

As described previously, aLINb ⇔ aSEQb ∨ bSEQa.
Finally, the OR relation is based on the # relation, but
is much more limited. It holds only when the SEQ
relation does not hold: aORb ⇔ a#b ∧ ¬(aLINb).
Consequently, the first step of the mining algo-
rithm is to partition the set of all task pairs (t
i
,t
j
),
i = 1, N, j = 1, N, i 6= j into three subsets of task
pairs that obey the original three relations →, k, and
#, respectively. This is done by means of establish-
ing the > relation first by performing a single scan of
all traces in the workflow log, identically to the oper-
ation of the α algorithm (van der Aalst et al., 2004).
The computational complexity of this step is linear in
the length of the workflow log, but is independent of
the number of tasks N. Establishing →, k, and # from
> can be done in time O(N
2
).
The resulting partition of task pairs can be rep-
resented conveniently in the matrix M
α
whose en-
try M
α
i, j
contains the relation label for the pair (t
i
,t
j
),
i = 1, N, j = 1, N, i 6= j. The diagonal entries M
i,i
,
i = 1, N are undefined and excluded from considera-
tion. Note that M
α
is not symmetric, in general.
The second step is to build the relation matrix M
of the workflow tree mining algorithm, whose entries
are based on the entries M
α
and the definitions de-
scribed above. The order of filling in the matrix M is
strictly as listed above: AND, SEQ, LIN, and OR, and
since LIN labels overwrite SEQ labels, the end result
is a partition of the task pair set into three relation
subsets labelled with AND, OR, and LIN. Again, the
diagonal elements of M are undefined and excluded
from consideration. Note that in contrast to M
α
, M is
symmetric. The complexity of this step is O(N
2
).
The third, and central, step of the algorithm is to
find the difference ∆
i, j
between each distinct pair of
rows (i, j), i 6= j in the matrix M, defined as ∆
i, j
=
∑
N
k=1
δ(i, j, k), for
δ(i, j, k)
.
=
1 iff i 6= k ∧ j 6= k ∧ M
i,k
6= M
j,k
0, otherwise.
(1)
If ∆
i, j
= 0 for a distinct pair of tasks (i, j), i 6= j,
this means that these two tasks have identical respec-
tive relations with respect to all remaining tasks, and
by virtue of Theorem 1 applied in the forward direc-
tion, they must have the same parent. In such case,
we can build a workflow subtree that has a root node
labeled with M
i, j
, and children t
i
and t
j
.
When more than one element ∆
i, j
= 0 (excluding
the symmetric element ∆ j, i which is also necessar-
ily zero because of the symmetry of ∆), it is not nec-
essarily always true that all corresponding nodes are
children of the same relation node. This is only true
when every pair of them (i, j) will have pairwise dis-
tance ∆
i, j
= 0 (from Theorem 1, applied in the reverse
direction.) In the general case, there might be sev-
eral sets of tasks, such that each pair of tasks t
i
and t
j
within the same set has distance ∆
i, j
= 0, but distances
between tasks from different sets are not zero. Such
distinct, non-overlapping sets of tasks can be deter-
mined easily by scanning the matrix ∆ row-wise, and
adding a task t
i
to an existing set only if its distance
∆
i j
to all other tasks t
j
in that set is zero; when it has
distance ∆
ik
= 0 to some other task t
k
thas is not in
any existing set, a new set is initiated with members t
i
and t
k
.
Once all such sets have been found, a sub-tree is
constructed for each of them. The root of this subtree
is labeled with the relation that holds among these
tasks. Due to the semantics of WF-trees, a sub-tree
is simply a composite task that can participate in a
higher-level block just like any other atomic task. Be-
cause of this, we can create a new task label for each
sub-tree so identified. Let the set of these new com-
posite tasks be T
new
; this set complements the initial
set of atomic tasks T . The tasks t
i
∈ T
new
are given
successive ordinal numbers beyond N. Let also the
atomic tasks that are members of one of the cliques be
defined as T
inc
; each task in T
inc
is a child of a member
of T
new
. Finally, let also a set T
act
of active tasks be
identified, and initialized at this point as T
act
:= T .
The complexity of this (third) step is O(N
3
), be-
cause it is dominated by the cost of computing the ma-
trix ∆. (As noted, identifying sets and building sub-
trees requires a single scan of ∆, or only O(N
2
).) The
next series of steps are largely similar to the one just
described, only they work on a progressively modified
active set of tasks. The newly created composite tasks
in T
new
are added to the set of active tasks T
act
, while
atomic tasks that have already been included in some
sub-tree are excluded from T
act
. New sub-trees are
again constructed on the current tasks in T
act
, and the
process is repeated until only one task remains in T
act
— the root of the entire WFT. For a detailed descrip-
tion of these steps, see (Nikovski and Baba, 2007).
The overall complexity of this series of steps is again
O(N
3
), because new rows and columns of the matri-
ces M and ∆ are introduced only for new composite
tasks, and there can be at most N −1 such tasks. Each
new row or column has O(N) elements, and the com-
putation of each element takes O(N).
The last step of the algorithm is to re-order the
children of all LIN nodes, so that the SEQ relation
among them holds, and re-label those nodes with the
label SEQ. This completes the construction of the
workflow tree. Since, by construction, each com-
posite node has at least two children, this workflow
tree is also compact. The complexity of this step
is O(N
2
logN), since the induced tree has at most
WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS
PROCESSES
35

N − 1 internal nodes, each of which has O(N) chil-
dren which are sortable in O(N logN) time. Based on
the complexity of each step, the overall computational
complexity of the algorithm is O(N
3
).
5 CONCLUSIONS
We have described a representation of business pro-
cesses called workflow trees that is intuitive and
matches the hierarchical organization of most busi-
ness processes used in practice. While similar to
other business process representations used in the
past, workflow trees have precise semantics and prop-
erties which derive directly from their tree-like repre-
sentation. These properties can be leveraged to devise
a computationally efficient process mining algorithm
that can recover business process models with concur-
rent tasks that have not been specified as such explic-
itly in workflow logs. The algorithm operates by an-
alyzing and comparing the mutual relations between
pairs of tasks, suitably organized in matrices, and this
determines its favorable computational complexity —
cubic in the number of process tasks.
This computational efficiency is achieved at the
expense of a slight sacrifice in the representational
power of workflow trees in comparison to other for-
malisms, such as workflow nets (van der Aalst et al.,
2004). The set of process models that can be repre-
sented by workflow trees is a strict subset of the set
of models that can be represented by workflow nets
— there exist some processes that can be represented
by workflow nets, but not by workflow trees, most no-
tably some processes with complex concurrency and
mixed synchronization.
A more serious limitation of the current version of
the mining algorithm is that it cannot recover models
with looped execution. While such models are eas-
ily represented by workflow trees, using several pos-
sible iterative constructs, the mining algorithm pro-
posed in this paper relies on the property of induced
trees that each of their internal nodes must have at
least two children. This effectively excludes iterative
constructs from the set of blocks that can be used for
building induced models.
However, this is not a principled restriction — in
fact, the presence of looped execution can easily be
detected as a by-product of computing the transitive
closure SEQ of the → relation. If there exists a task
a such that aSEQa, then the process must contain a
loop. However, identifying how many loops exist,
where the corresponding IT ER constructs should be
positioned in a workflow tree, and how the tree should
be mined in the presence of such constructs, is still an
open problem to be addressed by future work.
REFERENCES
Cook, J. E. and Wolf, A. L. (1998a). Discovering models
of software processes from event-based data. ACM
Trans. Softw. Eng. Methodol., 7(3):215–249.
Cook, J. E. and Wolf, A. L. (1998b). Event-based detection
of concurrency. In SIGSOFT ’98/FSE-6: Proceed-
ings of the 6th ACM SIGSOFT international sympo-
sium on Foundations of software engineering, pages
35–45, New York, NY, USA. ACM Press.
de Medeiros, A., van Dongen, B., van der Aalst, W., and
Weijters, A. (2004). Process mining: Extending the α-
algorithm to mine short loops. BETA Working Paper
Series, WP 113, Eindhoven University of Technology,
Eindhoven.
List, B. and Korherr, B. (2006). An evaluation of conceptual
business process modelling languages. In SAC ’06:
Proceedings of the 2006 ACM symposium on Applied
computing, pages 1532–1539, New York, NY, USA.
ACM Press.
Nikovski, D. and Baba, A. (2007). Workflow trees
for representation and mining of implicitly con-
current business processes. Technical Report
TR2007-072, Mitsubishi Electric Research Labs,
www.merl.com/publications/TR2007-072.
Schimm, G. (2004). Mining exact models of concurrent
workflows. Comput. Ind., 53(3):265–281.
Sedgewick, R. (2002). Algorithms in C. Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA.
Silva, R., Zhang, J., and Shanahan, J. G. (2005). Probabilis-
tic workflow mining. In KDD ’05: Proceeding of the
eleventh ACM SIGKDD international conference on
Knowledge discovery in data mining, pages 275–284,
New York, NY, USA. ACM Press.
van der Aalst, W., Weijters, T., and Maruster, L. (2004).
Workflow mining: Discovering process models from
event logs. IEEE Transactions on Knowledge and
Data Engineering, 16(9):1128–1142.
van der Aalst, W. M. P. and van Hee, K. M. (2002). Work-
flow Management: Models, Methods, and Systems.
MIT Press.
van der Aalst, W. M. P. and Weijters, A. J. M. M. (2004).
Process mining: a research agenda. Comput. Ind.,
53(3):231–244.
ICEIS 2008 - International Conference on Enterprise Information Systems
36
