ANOMALY DETECTION ALGORITHMS IN

BUSINESS PROCESS LOGS

F´abio Bezerra and Jacques Wainer

IC-UNICAMP, Campinas, S˜ao Paulo, Brazil

Keywords:

Anomaly Detection, Process Mining, Business Process Systems.

Abstract:

In some domains of application, like software development and health care processes, a normative business

process system (e.g. workﬂow management system) is not appropriate because a ﬂexible support is needed to

the participants. On the other hand, while it is important to support ﬂexibility of execution in these domains,

security requirements can not be met whether these systems do not offer extra control, which characterizes a

trade off between ﬂexibility and security in such domains. This work presents and assesses a set of anomaly

detection algorithms in logs of Process Aware Systems (PAS). The detection of an anomalous instance is based

on the “noise” which an instance makes in a process model discovered by a process mining algorithm. As a

result, a trace that is an anomaly for a discovered model will require more structural changes for this model

ﬁt it than a trace that is not an anomaly. Hence, when aggregated to PAS, these methods can support the

coexistence of security and ﬂexibility.

1 INTRODUCTION AND

MOTIVATION

In some application domains, such as software de-

velopment and hospital processes, the process con-

trol can not be normative as the control provided by

workﬂowmanagementsystems. In these domains, the

business process is not completely known before exe-

cution. For example, in a hospital process the system

can not obligate the execution of a speciﬁc task during

a care (e.g. administration of a drug). Even consider-

ing the similarity with other cases, such a care could

be unique, which demands a ﬂexible approach to its

participants (e.g. physician) that could be the right to

execute another task (e.g. request an examination).

On the other hand, a ﬂexible system is vulnera-

ble to fraudulent executions, which imposes a trade

off between ﬂexibility and security. Thus, it is impor-

tant to develop methods that can support the adoption

of such ﬂexible systems without losing their security

property. Since a BPMS (Business Process Manage-

ment Systems) usually log the events (or tasks) exe-

cuted during process execution, it would be interest-

ing to aggregate into a BPMS a tool that can dynami-

cally detect anomalous executions in the log. By and

large, a log generated by such systems is comprised

of process instances, referred in this work as traces,

which are a stream view of process instances. For

instance, a trace abc means that the task a was con-

cluded before task b, and task b was concluded before

task c.

A common intuition is to consider a fraudulent

execution an infrequent or rare event. Nevertheless,

this paper argue that although an anomalous trace is

an infrequent event, an infrequent trace not neces-

sarily indicates an anomaly, as will be shown later.

This premise imposes a challenge: What infrequent

trace could be classiﬁed as anomalous? This work

will present some algorithms that collaborate in this

mission, and it will asses the effectiveness of the pro-

posed anomaly detection solutions.

Moreover, despite the motivation related to prob-

lems stated above, anomaly detection is becoming an

exciting area within data mining arena, since many

surprising and rare events are of interest in security,

surveillance, epidemiology, fraud detection, among

others. However, to our knowledge, little effort has

been made with the investigation of anomaly detec-

tion algorithms in the context of process aware sys-

tems. The work in (van der Aalst and de Medeiros,

2005) represents an attempt to fulﬁll this gap, but it

is a limited solution because it assumes that a process

model is known or could be inferred from a known

“normal” log.

In order to deﬁne an anomaly detection tool, we

are interested in applying process mining techniques

Bezerra F. and Wainer J. (2008).

ANOMALY DETECTION ALGORITHMS IN BUSINESS PROCESS LOGS.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 11-18

DOI: 10.5220/0001674700110018

 SciTePress

to discover anomalies or outliers in the log. Pro-

cess mining were created to be used to discovery

or mine process models from logs (Agrawal et al.,

1998; Maruster et al., 2001; de Medeiros et al., 2003;

van der Aalst et al., 2004). For example, process

mining techniques can be used to discover how peo-

ple work, to support business process modeling, and

to diagnose the enterprise work practice (Hammori

et al., 2006). Another usage of process mining tech-

niques is to construct social networks as presented in

(van der Aalst Minseok Song, 2004). In the anomaly

detection algorithms of this work, the classiﬁcation of

an anomalous trace is based on the “noise” which a

trace makes in a process model discovered by a pro-

cess mining algorithm. These algorithms are based on

the rationale that if a trace is not an instance of a pro-

cess model, then the model will require some struc-

tural changes to the model ﬁt the trace. In the case of

an anomalous trace, such structural changes will be

probably higher.

In the next section we report some related work.

The process mining tool that is used to support the

anomaly detection methods is presented in Section 3.

Also in Section 3, we present the metric that is used

to quantify the “noise” made by a trace for a model ﬁt

it. After that, three different approaches of anomaly

detection in logs of PAS are presented in Section 4.

Conclusions and future work are in Section 6.

2 RELATED WORK

Anomaly detection is an exciting area which has been

applied in different application ﬁelds, and it has re-

ceived a special attention of data mining community.

For instance, in (Donoho, 2004) the author presents

how data mining techniques can be used to early de-

tect inside information in option trading. In (Fawcett

and Provost, 1997) the authors present a system which

is used to detect fraudulent usage of a cellular (cel-

lular cloning). Moreover, disease outbreak detec-

tion has been proposed by detecting anomalies in the

event logs of emergency visits (Agarwal, 2005), or

the retail data for pharmacies (Sabhnani et al., 2005).

There are solutions concerned with the intrusion de-

tection in networks (eg. (Lee and Xiang, 2001; Noble

and Cook, 2003)). Other efforts are concerned with

the detection of fraudsters in auctions or e-commerce

sites(e.g. (Pandit et al., 2007)).

Nevertheless, in the context of process aware sys-

tems, little effort has been done to the development of

anomaly detection methods. To our knowledge, only

the work in (van der Aalst and de Medeiros, 2005) is

closer related to our research. In that work the authors

present two methods whose support tool is a pro-

cess mining algorithm, the α-algorithm (van der Aalst

et al., 2004). In these methods, a known log com-

prised of “normal” traces is mined to deﬁne a classi-

ﬁer, whose function is audit a separated log. However,

those methods are not suited in some domains of ap-

plication because a “normal” log is not known or a

“normal” model can not be known before execution.

Differently, our approaches are applied directly over

the audit log, and they do not consider the existence

of a known model, nor do they consider the existence

of a log without anomalous traces.

The accuracy of our anomaly detection algorithm

can be related to three items: (i) the process mining

algorithm; (ii) the metric used to quantify the modiﬁ-

cation in a model for ﬁt a new trace (“noise” metric);

and (iii) the process model representation. Therefore,

it would be interesting to assess other process mining

algorithms. For example, the algorithm described in

(Schimm, 2004) mines a similar process model rep-

resentation (block-structured models). Perhaps other

process mining approaches could be used, e.g. α-

algorithm (van der Aalst et al., 2004) or genetic min-

ing (de Medeiros et al., 2006); however, these process

mining algorithms utilize other process model repre-

sentation, so they will demand another metric to eval-

uate the inclusion cost of a trace. In the context of

“noise” metric, the set of conformance check metrics

presented in (Rozinat and van der Aalst, 2005) could

be assessed.

3 INCLUSION COST AND

INCREMENTAL PROCESS

MINING

The inclusion cost is a metric used to evaluate the

amount of modiﬁcations done in an old process model

in order to deﬁne a new process model which ﬁts a

merged trace. Thus, to cope with such a metric, it

is important to use a process mining algorithm which

incrementally deﬁne a process model. In this work

we adopted the incremental process mining algorithm

based on rewriting rules, presented in (Wainer et al.,

2005). Such a mining algorithm discovers a model

whose meta-model is based on a combination meta-

models presented in (Agrawal et al., 1998; Cook and

Wolf, 1998). The meta-model presented in (Cook

and Wolf, 1998), which is based on selection struc-

tures (OR), deﬁne models that are syntactically more

complex than the models deﬁned by the meta-model

presented in (Agrawal et al., 1998), which is based

on parallel structures (AND). For example, while the

ICEIS 2008 - International Conference on Enterprise Information Systems

T = { t1, t2, t3 }

t1 + t2

M1 M2 M3 Mn. . .

If M3 is the smallest,

M3 is selected

M3 + t3

If M31 is the smallest,

M31 is selected

M31 M32 M33 M3n. . .

FINISH

CONTINUE

M31 is the

mined model

for set T

Figure 1: Greedy search for traces in set T.

and

T = { abcd, acbd, abce }

and

Size = 6

Size = 9

Size = 4

abcd acbd

M abce

Figure 2: Mining example of a set of traces T.

parallelism between three tasks can be easily rep-

resented by an AND-Block, using an OR-Block it

would demand six selection branches. On the other

hand, the meta-model presented in (Cook and Wolf,

1998) deﬁnes models whose expressiveness is greater

than the models deﬁned by meta-model presented in

(Agrawal et al., 1998). Therefore, a mix of these

approaches represents a balance between complexity

and expressiveness.

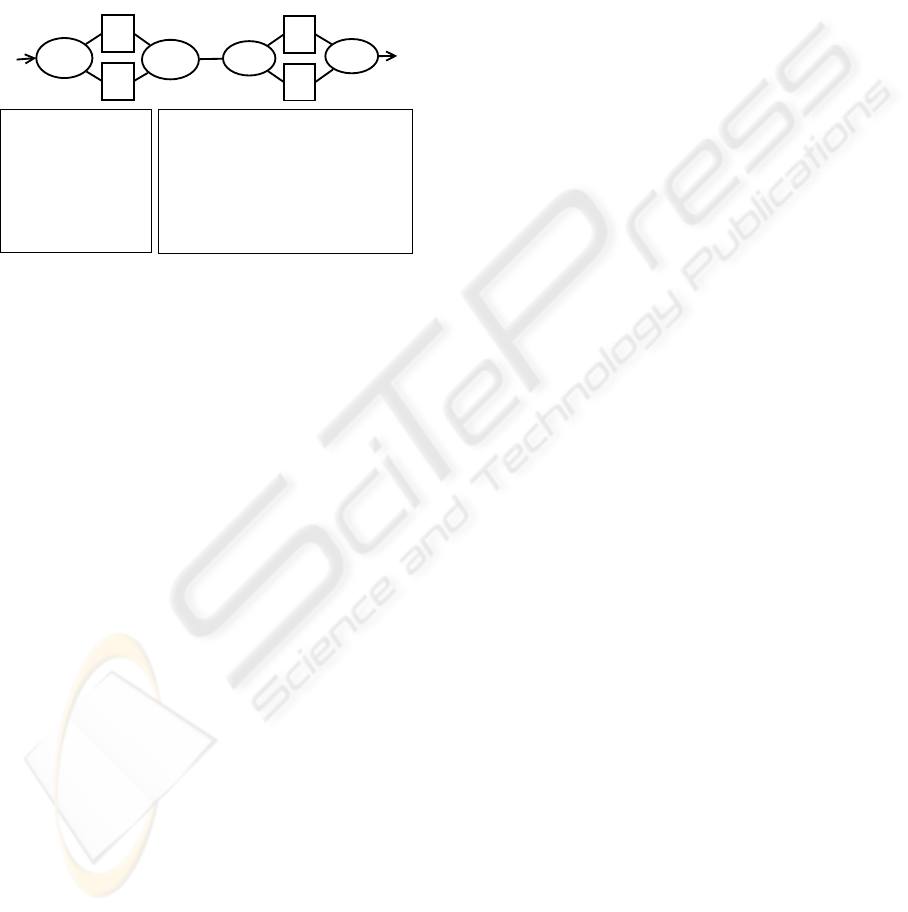
The model is a directed graph M = (V(M), E(M))

whose verticesV(PM) are the tasks or AND/OR con-

structs (split and join), while the edges E(PM) repre-

sent the play order of its vertices. For example, Fig-

ure 2 depicts three process models whose tasks are

represented by a labeled rectangle while AND-Blocks

and OR-Blocks are represented by a labeled ellipse.

AND-Blocks indicate a parallelism, and OR-Blocks

indicate a choice. The Equation 1 illustrates how the

inclusion cost is evaluated for a trace t ∈ T, such that

T is a set of different traces of a log. It is based on two

process models deﬁned through the incremental pro-

cess mining algorithm – an old model (M

), which is

created with the traces T − t, and a new model (M

which is created with the traces T.

IC(M

, M

) = |V(M

)| − |V(M

)| (1)

Such an incremental mining algorithm constructs

a model through the amalgamation of a trace over a

model, which could be modiﬁed, generating another

model. After that, another trace of log will be merged

generating a new model, an so on. The procedure

ﬁnishes when all unique traces were merged, result-

ing a process model. The incremental construction is

based on a set of rules classiﬁed as (i) structural rules

and (ii) introduction rules. The structural rules do

not change a model, but they are used to identify the

points of application of the introduction rule, whereas

the introduction rules introduce structural blocks such

as AND/OR Split/Join. The algorithm tries to amal-

gamate a trace into a model in different ways, either

applying different sequences of rules, or merging the

traces in a different sequence. Therefore, it has two

drawbacks that imposes serious limitations of its us-

age on larger logs, which are the large search space

generated by the rules and the amount of models gen-

erated at the end of mining.

To solve this limitation we added a greedy search

for minimal models after the amalgamation of each

trace. Figure 1 illustrates schematically how the pro-

cess mining works on a log of three traces. Among

all derived models, we select the smallest one. A

model M is smaller than a model M’ if M has less

vertices than M’. The selection of the smallest model

reduces the search space, so it improves the execution

time of algorithm. In addition, such an algorithm re-

turns a structured model that ﬁts all traces and is likely

minimal, which are requirementsof completeness and

minimality as stated in (Schimm, 2004; Rozinat and

van der Aalst, 2005).

Figure 2 illustrate how a process mining works.

The ﬁgure shows three models generated when min-

ing a set of traces T = {abcd, acbd, abce}. The ﬁrst

trace abcd deﬁnes a sequential model whose size is

four. Then, the second trace acbd is merged with the

sequential model, and a bigger model of size six is

generated for ﬁtting the merged trace. Finally, the

ANOMALY DETECTION ALGORITHMS IN BUSINESS PROCESS LOGS

third trace abce is merged, generating a third model

with size nine. Therefore, this simple example illus-

trates how the inclusion of a trace can produce a mod-

iﬁcation in the model.

4 ANOMALY DETECTION

METHODS

Possible traces

a - b - c

a - b - d

b - a - c

b - a - d

Some incomplete logs

a - b - c

a - b - d

b - a - c

OR (c, d)

AND (a, b)

a - b - c

b - a - c

b - a - d

AND (a, b)

OR (c, d)

and

a - b - c

a - b - d

b - a - d

OR (c, d)

AND (a, b)

Figure 3: Mining of a process model with an incomplete

log.

Despite the different semantics associate with an

anomalous trace (e.g. noise, exception, or fraud), for

the purpose of this work an anomalous trace is an ir-

regular execution that differs from a process model

which was dynamically discovery during anomaly de-

tection process. This work adopts this approach be-

cause in some application domains a complete pro-

cess model is not known before execution. There-

fore, it is hard to adopt a precise deﬁnition of what

an anomalous trace is. On the other hand, a common

presupposition in literature is to consider an anomaly

like a rare event. However, classifying a trace based

only on its frequency in the log is not simple since it is

probable that some “normal” traces be infrequent, for

some “normal” operational procedures are preferable

than others. Moreover, it would be very difﬁcult to

deﬁne a frequency which better describes an anoma-

lous trace. For instance, it does not seem appropriate

to classify as anomalous all traces whose frequency is

inferior to 5%.

Figure 3 depicts a process model, its possible

traces, and some subset of possible traces that can

reconstruct the same model. A possible trace is an

execution instance of a model, so the tasks a and b

have to appear in a possible trace of model in Figure

3 while c and d do not. In the ﬁrst incomplete subset,

the ﬁrst pair of traces ([a− b − c] and [a− b− d]) in-

ducts an “OR Block” to represent a choice (OR (c, d)),

while the last pair of traces ([a−b−d] and [b−a−d])

inducts an “AND Block” to represent a parallelism

(AND (a, b)). In this example, the trace [b− a − c]

is an instance of original model although it has not

been used to mine it. Thus, even if it was infrequent

in the log, it would not be possible to classify it like an

anomalous trace. Therefore, how to classify a (rare)

trace in the log as an anomalous one?

The anomaly detection methods adopt the follow-

ing hypothesis: most of the “normal” traces, if taken

individually, will be more frequent than anomalous

traces, and anomalies and a few “normal” traces will

be rare in the log. The traces that are not anomalies

when mined should generate a process model, and try-

ing to ﬁt the anomaly into this model will require a

lot of structural changes in the models; therefore an

anomaly is the trace whose inclusion produces a large

modiﬁcation to the model generated by other traces in

the log.

1. T is a list of all different traces of L;

2. For each t ∈ T do

3. Deﬁne a list L

′

= {L without one instance of t};

4. Deﬁne a sampling S with 50% of traces from L

′

;

5. Create a model M based on traces of S;

6. If t is not instance of M then

7. Add t to list A;

Figure 4: Anomalous trace classiﬁer based on sampling.

The algorithm of Figure 4 will consider each of

the unique traces in the log as a possible anomaly, and

each candidate will be an anomaly if it is not an in-

stance of a process model created with a sampling of

log. The sampling comprises 50% of traces from log,

and it is redeﬁned for each unique trace of log. The

composition of sampling is crucial because if anoma-

lies are rare as assumed, the set S will unlikely contain

an anomaly itself. Thus it can be seem as a sampling

of the “normal” traces, so it would reveal a approxi-

mation of the “normal” model.

Nevertheless, there are many things that can go

wrong with such assumptions and thus with the algo-

rithm. For example, the set S can comprise anoma-

lies which “contaminates” the mined model M; thus,

t could be an instance of M even though it may be

anomaly. That danger can be lessen by reducing the

size of the sample S. On the other hand, if the size

of S is too small, it may not be a large enough sam-

pling of the “normal” model because a too simple

“normal” model will be mined, so a “normal” trace

may be marked as anomalous.

The algorithm of Figure 5 classiﬁes a trace as

anomalous if such a trace has the highest inclusion

cost, and its cost is higher than 2 (lines 4 and 9). This

approach is called iterative because it is repeated until

there is not such a trace in the log. The select(C, F)

ICEIS 2008 - International Conference on Enterprise Information Systems

1. T is a list of all different traces of L;

2. F is a list of frequent traces in log;

3. C = T − F is a list of anomalous candidate traces;

4. h ← select(C, F);

6. While inclusion cost of h is higher than 2;

7. Add h to list A;

8. Remove h from list C;

9. h ← select(C, F);

Figure 5: Iterative anomalous trace classiﬁer.

function returns nil or one trace that has the highest

inclusion cost, and the inclusion cost of each candi-

date t is evaluated based on a model constructed with

the traces from C∪ F − {t}.

The step in line 2 select all frequent traces in the

log. We say that a trace is frequent if its frequency is

at least 10%. Such a step is used for optimization rea-

sons, because the next (line 3) reduces the number of

candidate anomalous traces. However, even with that

optimization, the select(C, F) function may compro-

mise the execution time of whole algorithm.

The stop condition threshold represents our be-

lief that even a “normal” trace may demand struc-

tural changes in a model mined with the remaining

traces of a log, but possibly in a smaller scale. How-

ever, although such a threshold is a heuristic value, it

was induced by an assessment done with 150 “nor-

mal” logs. We say that such logs are “normal” be-

cause they are based on traces of a know model that

was randomly created for each log. In our intuition,

knowing the values and frequencies of inclusion cost

of traces in scenarios of “normal” logs, an inclusion

cost threshold for a “normal” trace could be inferred.

In this assessment, we collected the inclusion cost of

each unique trace for each log, and we evaluates some

statistic metrics of these costs, as follows: 1st quar-

tile = 0; median = 0; 3rd quartile = 2; mean = 1.306;

min = 0; and max = 7.

The algorithm of Figure 6 is similar to the itera-

tive algorithm presented in Figure 5, but it selects all

anomalous traces in a single step. Similarly, it uses a

threshold value to classify the traces as anomalous or

normal. Therefore, is has an execution time smaller

1. α=2; {A threshold amount of modiﬁcation}

2. T is a list of all different traces of L;

3. F is a list of frequent traces in log;

4. C = T − F is a list of anomalous candidate traces;

5. For each t ∈ C do

6. M is a model mined with traces from T − t;

7. c is the inclusion cost of trace t over M;

8. If c ≻ α then

9. Add t to list A;

Figure 6: Anomalous trace classiﬁer based on threshold.

than the iterative approach, because all anomalous

traces are identiﬁed in the ﬁrst and unique iteration.

Although we have used constant values for thresh-

old and sampling factor in the algorithms, we know

that a variance in these values could inﬂuence their

accuracy. For example, if we increase these values,

possibly the true (TPR) and false (FPR) positive ratios

would decrease. Nevertheless, the values presented in

each algorithm represent the best accuracy conﬁgura-

tion of our preliminary tests.

5 ASSESSMENT OF

ALGORITHMS

We have assessed the algorithms with a set of syn-

thetic logs which have been created based on the

traces of known process models. Two reasons inﬂu-

enced our choice for synthetic data. First, it is hard

(perhaps inexact) to identify an anomalous trace in a

real log, so it would impose some limitations on the

assessment. For example, in (Pandit et al., 2007) the

authors report some problems regarding the assess-

ment of their anomaly detection system with real data.

Last but not least, a real log is not available. There-

fore, as we know the process model that was used to

create a log, it is easy to identify the anomalous traces

in the log since an anomalous trace is a trace that is

not an instance of a known model.

5.1 Methodology

The experiments were based on 780 logs with differ-

ent conﬁgurations. Initially, we randomly created 130

process models which were the matrix of logs. Such

models could instance at least 8 unique traces and at

most 15 unique traces. For each model, we instanced

80 traces that were used to compose the log and rep-

resent the normal traces to the experiment. In addi-

tion, the unique traces of each log were added in a

non uniform frequency distribution. After that, we

merged some anomalous traces to deﬁne six types of

log, as follows: (i) a log A that has one single anoma-

lous trace; (ii) a log B that has two single anoma-

lous traces; (iii) a log C that has three single anoma-

lous traces; (iv) a log D that has one double anoma-

lous trace; (v) a log E that has two double anomalous

traces; and (vi) a log F that has three double anoma-

lous traces.

With regard to the anomalous traces, they were

generated as instances of a process model created

after shifting AND-Blocks to OR-Blocks, and vice

versa. Such a process model is known only during log

ANOMALY DETECTION ALGORITHMS IN BUSINESS PROCESS LOGS

and

Possible traces

a - b - c

a - b - d

b - a - c

b - a - d

Possible traces

a - d - c

a - c - d

b - d - c

b - c - d

Figure 7: Example of deﬁnition of anomalous traces.

generation, but it is unknown during anomaly detec-

tion assessment. The instances of this new (shifted)

process model are used to deﬁne the anomalous traces

for the original model. Then, after an instance has

been created some events could be removed of the

trace, or two random events could be interchanged.

Figure 7 illustrates an example of deﬁnition of

anomalous traces. The possible traces of upper model

are anomalous for the lower model, and vice-versa. In

this example, while the tasks c and d could not play

together in the upper model, they are played together

in the lower model. Moreover, while the tasks a and b

would have to play together in the upper model, they

are not played together in the lower model. Besides,

the approach used to create the anomalous traces rep-

resents our intuition that anomalous traces are similar

to “normal” traces, for they are based on the same set

of tasks. In other words, we believe that in real scenar-

ios a fraudster will not attempt to execute new tasks,

but he will try to make “little changes” in a standard

operational procedure, because it will be more difﬁ-

cult that his fraud be detected.

After the deﬁnition of logs, we carried out the ex-

periments with the three algorithms described in Sec-

tion 4. The results were organized in three classes:

(i) logs with single anomalous traces (A, B, and C);

(ii) logs with double anomalous traces (D, E, and F);

and (iii) all logs (A, B, C, D, E, and F). The following

subsection describes the results.

5.2 Results

Figures 8, 9, and 10 depict a graphical analysis tool

(ROC graphs, (Fawcett, 2004)) utilized to compare

the performance of the three proposed anomaly detec-

tion algorithms (or classiﬁers) in three different sce-

narios. Each point in those ﬁgures represent one of

the three algorithms, labeled as follows: S for sam-

pling approach; I for iterative approach; and T for

threshold approach. In a ROC curve, the best clas-

siﬁer is that one closer to optimal point of coordinates

(0, 100). The x-axis represents the ratio of false pos-

itives (FP rate), and the y-axis represents the ratio of

true positives (TP rate). The diagonal line in the cen-

Figure 8: Logs with at most three single or three double

anomalous traces.

Figure 9: Logs with at most three single anomalous traces.

Figure 10: Logs with at most three double anomalous

traces.

ICEIS 2008 - International Conference on Enterprise Information Systems

Figure 11: Assessment Summary.

ter of graph is used to identify good or bad classiﬁers.

Points above the diagonal line indicate good systems,

while points below the line indicate bad systems. The

ﬁgures illustrate a convex curve that is tangent to the

iso-performance classiﬁers, that is, classiﬁers that are

possibly optimal. Moreover, there is an upper line

that is tangent to the curve, where it touches the opti-

mal classiﬁer. The inclination of line depends on the

number of positives examples (anomalous traces) in

the data, which in the case of this assessment were

25%.

Figure 11 shows a summary of results in the fol-

lowing scenarios: logs with single anomalous traces;

logs with double anomalous traces; and logs with

single or double anomalous traces. It presents three

performance metrics, as follows: ACC indicates the

accuracy of algorithm, that is, how many traces in

the log were correctly classiﬁed; TPR, which is an

acronym of True Positive Rate, indicates the ratio of

anomalous (positive) traces that were correctly classi-

ﬁed; and FPR, which is an acronym of False Positive

Rate, indicates the ratio of normal (negative) traces

that were incorrectly classiﬁed.

Among the algorithms, the sampling approach had

the best accuracy either in the scenario of logs with

single anomalous traces or in the scenario of all logs.

However, such an approach was sensible to repetition

of anomalous traces in the log; as one can notice in

Figure 11, the threshold approach had the best accu-

racy rate in the scenario of logs with double anoma-

lous traces. Also, the TPR of sampling approach was

signiﬁcantly smaller than the others in the scenario

of logs with double anomalous traces. That perfor-

mance difference is justiﬁed. The sampling approach

is based on the instance traces, while iterative and

threshold approaches are based the unique traces.

Considering the execution time of algorithms, the

sampling approach had the best performance. The av-

erage time of execution for algorithms were as fol-

lows: 4.896 s for sampling approach; 9.016 s for

threshold approach; and 16.275 s for iterative ap-

proach. In the worst case, the algorithms were exe-

cuted in the following times: sampling = 466.422 s;

threshold = 670.625 s; and iterative = 1145.160 s.

6 CONCLUSIONS

Normative information systems are not appropriate in

application domains like software development and

health care processes, because users needs a ﬂexible

support. On the other hand, such a ﬂexibility in these

systems can not be considered without improving se-

curity issues. Besides, little attention has been given

to the anomaly detection area in the context of busi-

ness process systems. To fulﬁll this gap this work pre-

sented three different approaches to detect anomalous

traces in a log of process aware systems.

Despite the application context of algorithms has

been presented for security in ﬂexible environments,

such algorithms are a proposal to detect anomalies,

which have a larger semantic. For example, in the

context of software development one could apply the

algorithms to detect exceptions, while in process min-

ing context one could use the algorithms to remove

noise of logs before mining a model.

Several examples have been treated by our im-

plementation. Considering the results, the sampling

algorithm demonstrated to be a good solution, es-

pecially when applying it on logs without repeated

occurrences of anomalous traces. Nearly 99% of

anomalous traces were correctly identiﬁed, yet ap-

proximately 11% of “normal” traces were incorrectly

classiﬁed (false positives). Thus, the accuracy rate

can be improved reducing the cost of anomalous iden-

tiﬁcation. To do so, we deﬁned a research agenda

to achieve such an improvement, either testing other

process mining algorithms, or testing other metrics of

model modiﬁcation. Also, the sampling approach was

less time consuming among the tested algorithms.

ACKNOWLEDGEMENTS

This work was supported by fellowships of CAPES

and CNPq, which are Brazilian research agencies.

Moreover, the authors would like to thank the anony-

mous revisions.

ANOMALY DETECTION ALGORITHMS IN BUSINESS PROCESS LOGS

REFERENCES

Agarwal, D. K. (2005). An empirical bayes approach to

detect anomalies in dynamic multidimensional arrays.

In ICDM, pages 26–33.

Agrawal, R., Gunopulos, D., and Leymann, F. (1998). Min-

ing process models from workﬂow logs. In EDBT

’98: Proceedings of the 6th International Conference

on Extending Database Technology, pages 469–483,

London, UK. Springer-Verlag.

Cook, J. E. and Wolf, A. L. (1998). Discovering models

of software processes from event-based data. ACM

Trans. Softw. Eng. Methodol., Vol. 7(3):p. 215–249.

de Medeiros, A., van der Aalst, W., and Weijters, A. (2003).

Workﬂow mining: Current status and future direc-

tions. In Meersman, R., Tari, Z., and Schmidt, D.,

editors, On The Move to Meaningful Internet Systems,

volume 2888 of LNCS.

de Medeiros, A. K. A., Weijters, A. J. M. M., and van der

Aalst, W. M. P. (2006). Genetic process mining: A

basic approach and its challenges. Lecture Notes in

Computer Science, 3812:203–215. ISSN 0302-9743.

Donoho, S. (2004). Early detection of insider trading in op-

tion markets. In KDD ’04: Proceedings of the tenth

ACM SIGKDD international conference on Knowl-

edge discovery and data mining, pages 420–429, New

York, NY, USA. ACM Press.

Fawcett, T. (2004). Roc graphs: Notes and practical consid-

erations for researchers.

Fawcett, T. and Provost, F. (1997). Adaptive fraud detec-

tion. Data Mining and Knowledge Discovery, Vol.

1:p. 291–316.

Hammori, M., Herbst, J., and Kleiner, N. (2006). Interactive

workﬂow mining - requirements, concepts and imple-

mentation. Data Knowl. Eng., Vol. 56(1):p. 41–63.

Lee, W. and Xiang, D. (2001). Information-theoretic mea-

sures for anomaly detection. In IEEE Symposium on

Security and Privacy.

Maruster, L., van der Aalst, W. M. P., Weijters, T., van den

Bosch, A., and Daelemans, W. (2001). Automated

discovery of workﬂow models from hospital data. In

Krse, B., Rijke, M., Schreiber, G., and Someren, M.,

editors, Proceedings of the 13th Belgium-Netherlands

Conference on Artiﬁcial Intelligence (BNAIC 2001),

pages 183–190.

Noble, C. C. and Cook, D. J. (2003). Graph-based anomaly

detection. In KDD ’03: Proceedings of the ninth ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, pages 631–636, New York,

NY, USA. ACM Press.

Pandit, S., Chau, D. H., Wang, S., and Faloutsos, C. (2007).

Netprobe: a fast and scalable system for fraud de-

tection in online auction networks. In WWW ’07:

Proceedings of the 16th international conference on

World Wide Web, pages 201–210, New York, NY,

USA. ACM Press.

Rozinat, A. and van der Aalst, W. M. P. (2005). Confor-

mance testing: Measuring the ﬁt and appropriateness

of event logs and process models. In Business Process

Management Workshops, pages 163–176.

Sabhnani, R., Neill, D., and Moore, A. (2005). Detecting

anomalous patterns in pharmacy retail data. In Pro-

ceedings of the KDD 2005 Workshop on Data Mining

Methods for Anomaly Detection.

Schimm, G. (2004). Mining exact models of concurrent

workﬂows. Comput. Ind., Vol. 53(3):p. 265–281.

van der Aalst, W. M. P. and de Medeiros, A. K. A.

(2005). Process mining and security: Detecting

anomalous process executions and checking process

conformance. Electr. Notes Theor. Comput. Sci., Vol.

121:p. 3–21.

van der Aalst, W. M. P., Weijters, T., and Maruster, L.

(2004). Workﬂow mining: Discovering process mod-

els from event logs. IEEE Trans. Knowl. Data Eng.,

Vol. 16(9):p. 1128–1142.

van der Aalst Minseok Song, W. M. (2004). Mining social

networks: Uncovering interaction patterns in business

processes. In Desel, J., Pernici, B., and Weske, M.,

editors, Business Process Management: Second Inter-

national Conference, volume 3080 of LNCS, pages pp.

244 – 260.

Wainer, J., Kim, K., and Ellis, C. A. (2005). A workﬂow

mining method through model rewriting. In Fuks, H.,

Lukosch, S., and Salgado, A. C., editors, Groupware:

Design, Implementation, and Use: 11th International

Workshop, volume 3706, pages p. 184–19, Porto de

Galinhas, Brazil. CRIWG 2005.

ICEIS 2008 - International Conference on Enterprise Information Systems