AN IMPLEMENTATION OF XML DATA INTEGRATION

Weidong Pan, Jixue Liu and Jiashen Tian

School of Computer and Information Science, University of South Australia

Mawson Lakes, Adelaide, SA 5095, Australia

Keywords:

XML, data Integration, enterprise inﬁormation sytsem, DTD, document, data transformation.

Abstract:

Data integration is essential for building modern enterprise information systems. This paper investigates the

implementation of XML data integration through transforming XML data from different data sources into a

common global schema. Following the work our research group has done earlier, the paper is focused on the

implementation of XML data transformation. First, the proposed methodology to realize XML data integration

is sketched. Then, the representation of a DTD and document and other relevant concepts for transforming

XML data are presented. The transforming operations deﬁned by a set of operators are outlined focusing on the

required functionality for data integration. Building upon these, the implementation of the data transformation

operations is investigated. The current implementation is reported with a simpliﬁed example illustrating how

the methodology can be applied for practical enterprise information integration.

1 INTRODUCTION

Data integration is essential for building modern en-

terprise information systems since data is normally

distributed on different platforms. In order to inte-

grate these data together to provide a unique view

for users, there is a need for technologies to imple-

ment the conversion of data from different sources to

a common uniﬁed schema. Since XML has been in-

creasingly used for data representation and exchange

across the Internet, it is of speciﬁc importance to in-

tegrate XML data from multiple data sources into a

global schema with a unique structure. This paper

investigates the implementation of XML data inte-

gration, more speciﬁcally, it aims to realize the inte-

gration through converting XML data from different

schemas into a uniﬁed global schema.

A number of earlier research has devoted to XML

data integration. The techniques proposed can be

summarized into two main procedures, scheme map-

ping and data conversion. The former aims to de-

velop techniques to map XML data from different

sources to a common global schema, through which

XML data distributed at different sources can be rep-

resented in a unique view; the latter aims to, based

on the mapping between an original and a destina-

tion schema, develop techniques to convert XML data

from different sources into a destination platform that

conforms to an integrated global schema. Data con-

version can be done through query processing or ex-

ecuting a sequence of transformation operations. By

query processing, users retrieve data from a document

and then build another document using the retrieved

data. W3C’s XQuery (Boag et al., 2007) and XSLT

(Kay, 2007) are two typical query languages. Data

conversion can also be implemented by executing a

sequence of data transformation operations deﬁned by

a set of operators. Data transformation operators have

been proposed in a number of previous work, some

are similar to XML algebra expressions derived from

relational data model (Zamboulis, 2004). In general,

they just provide operators for XML document update

and have not provided a systematic set of transforma-

tion operators with a clear semantic. Although a few

has considered DTD transformation when document

is being transformed (Erwig, 2003), none has covered

the full DTD syntax. In addition, to the best of our

knowledge, the implementation issue of the operators

has not been well addressed and accordingly their per-

formance has not been deeply studied from the view-

points of practical applications.

To address these problems, our research group has

proposed a set of XML data transformation operators

to realize XML data integration (Liu et al., 2006).

Compared with other data transformation operators,

our operators include two types of transformation: 1)

DTD transformation, and 2) document transforma-

tion. This can ensure the output documents of the

operators always conform to the output DTDs, which

is critical to the semantics of output data. Our op-

erators are deﬁned with the consideration of the full

syntax of DTDs and documents, especially the nested

111

Pan W., Liu J. and Tian J. (2008).

AN IMPLEMENTATION OF XML DATA INTEGRATION.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - DISI, pages 111-116

DOI: 10.5220/0001677401110116

 SciTePress

brackets in element type deﬁnitions, multiplicity con-

straints attached to those nested brackets, and disjunc-

tion. They are complete for the transformation of

DTDs and documents. In addition, they are semanti-

cally traceable when being used to realize XML data

integration; each has a particular intention and creates

a particular semantic effect towards the overall goal.

Up to this point, we have completed a preliminary im-

plementation of these operators using Java and JSP

techniques. This paper is to report our recent research

in XML data integration, focusing on the implemen-

tation of the operators, as the performance analysis

for the operators has been presented in another paper

(Tian et al., 2008).

The paper is organized as follows. In Section 2, an

overview of the proposed methodology is presented.

Section 3 illustrates the representation of XML data,

providing some essential concepts and terms. Section

4 describes the data transformation operations deﬁned

by the data transformation operators. Section 5 looks

into the implementation of the operators. Section 6 re-

ports the current implementation and presents a sim-

pliﬁed example to illustrate how the approach is used

in practical enterprise information integration appli-

cations. The ﬁnal section summarizes the paper and

indicates the further work.

2 OVERALL DESCRIPTION OF

OUR METHODOLOGY TO

REALIZE XML DATA

INTEGRATION

As stated in the previous section, what we aim to

achieve is XML data integration by converting XML

data to a uniﬁed schema from different sources with-

out losing valuable semantic information. It is com-

plicated by the ﬂexible XML syntax that allows differ-

ent ways to represent the data of same semantics. We

realize XML data conversion using a set of transfor-

mation operators that supply enough transformation

power and preserve the data semantics to a certain de-

gree.

The proposed methodology to achieve XML data in-

tegration is through data transformation. All the

DTDs and the conforming documents from different

data sources are converted to a uniﬁed XML format

that conforms to the integrated global schema. As

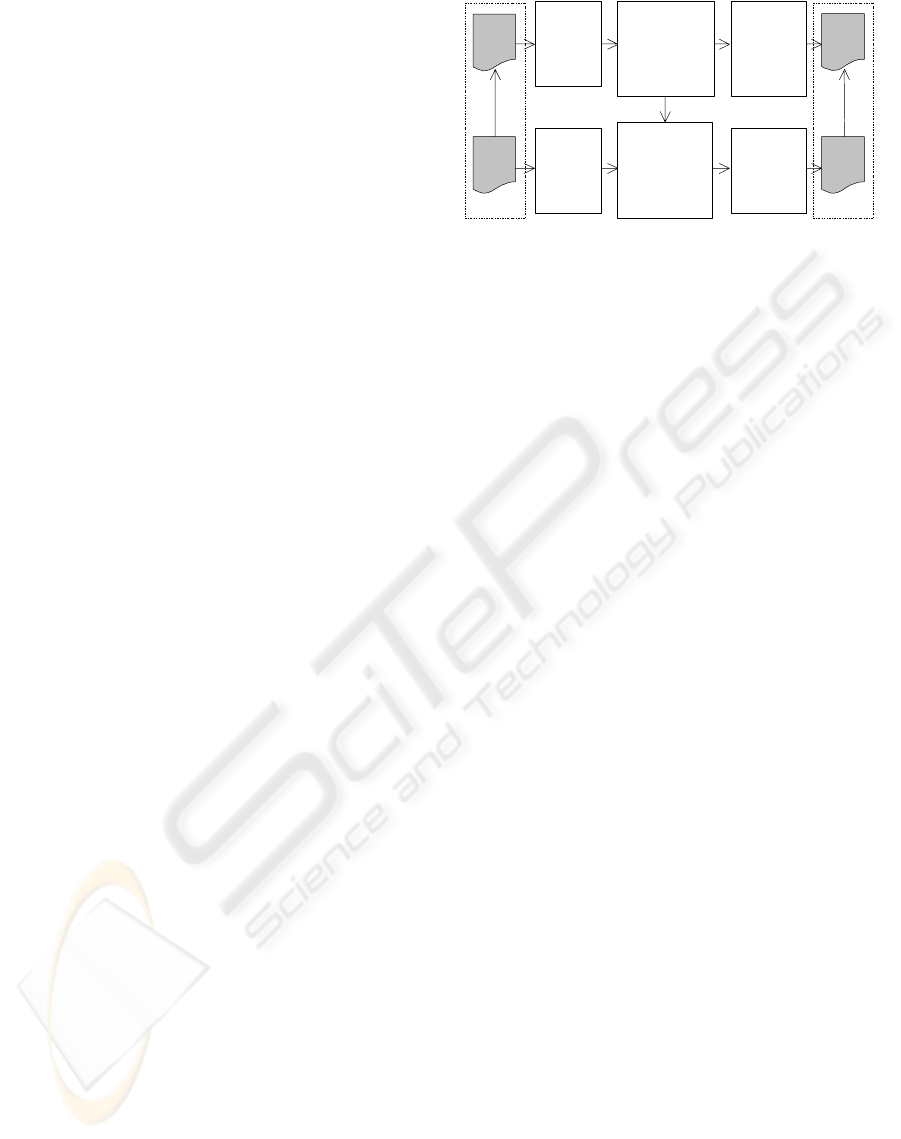
illustrated in Figure 1, in the conversion of a DTD

from a particular source, a four-tuple expression is

built based on the given DTD ﬁle. Then, the tuple ex-

pression is transformed to a new one through execut-

ing a sequence of data transformation operations, de-

DTD

file

Source

conforms to

XML

file

Destination

Trans

form the

document trees

by executing a

series of

transformation

operations

Restore the

transformed

tuple

expression

into a DTD

file

Restore the

transformed

document

trees into an

XML file

supplies

information

conforms to

DTD

file

XML

file

Transform the

tuple expression

by executing a

series of

transformation

operations

Build

document

trees from

the XML

file

Build a

four-tuple

expression

from the

DTD file

Figure 1: Framework for XML data transformation.

ﬁned by a set of operators. After the transformation,

the new tuple expression is restored into a new DTD

ﬁle, achieving a conversion from the previous DTD

to a new one. The transformation of an XML doc-

ument from a particular source to a targeted schema

has a similar process except that it requires the sup-

port from the transformation of its conformed DTD

to ensure the output document has a compatible se-

mantic structure.

In the sections that follow, we will elaborate the

methodology outlined here.

3 XML DATA REPRESENTATION

3.1 DTD Representation

A DTD deﬁnes the structure of its corresponding doc-

uments by a list of element type declarations. In the

proposed approach, this information is represented by

a four-tuple D = (EN, G, β, ρ), where EN is the set of

the element names in the DTD; G is the set of type

constructors which deﬁne the elements; β is the set of

the functions connecting an element with its type con-

structor; and ρ is the root of the DTD. Figure 2 shows

a simpliﬁed DTD example and its corresponding tu-

ple expression. It is extracted from a DTD used in a

publishing company for publication information.

Note, to save space, the headers and the string type

#PCDATA in the DTD are intentionally left out. An

element in G can be a single element, or a component

including multiple elements in conjunctive or disjunc-

tive sequences. For example, if g ∈ G, then g can be in

the following forms: g = e (e ∈ EN), g = Str (Str is a

symbol denoting #PCDATA), or g = g

, g

or g

[g]

, where g

and g

are recursively deﬁned, and c ∈

{‘?’, ‘1’, ‘+’, ‘∗’}. The multiplicity c deﬁnes the mul-

tiplicity constraints of g. Transforming a DTD also

involves the transformation of the multiplicities. For

handling multiplicities, ‘?’, ‘1’, ‘+’ and ‘∗’ are rep-

resented by the intervals [0, 1], [1, 1], [1, n] and [0, n],

ICEIS 2008 - International Conference on Enterprise Information Systems

112

<!ELEMENT root (name,publ)*>

<!ELEMENT publ (year,(book|article)+)*>

<!ELEMENT book (title,ISBN, price)>

<!ELEMENT article (title,journal,issue?,page)>

(a) A Simpliﬁed DTD example

EN = {root, name, publ, year, book, article, title, ISBN,

price, journal, issue, page}

G = {Str, [name, publ]

∗

, [year, [book|article]

]

∗

, [title,

ISBN, price], [title, journal, issue

, page]}

β(root) = [name, publ]

∗

, β(publ) = [year, [book|article]

]

∗

β(book) = [title, ISBN, price],

β(article) = [title, journal, issue

, page],

β(year) = β(name) = β(title) = β(ISBN) = β(price) =

β( journal) = β(issue) = β(page) = Str.

(b) The tuple expression of the DTD example

Figure 2: A DTD example and its tuple expression.

respectively. The operations of two multiplicities c

and c

are conducted relying on the operations of their

intervals. Thus, c

⊕ c

(= c

) has the semantics of

the multiplicity whose interval encloses the intervals

of c

and c

, e.g., +? = ∗ and 1? =?. Similarly, c

c

is the multiplicity whose interval equals to the inter-

val of c

taking that of c

and adding that of 1, e.g.,

?? = 1 and ∗  + =?.

3.2 Document Representation

A well-formed XML document is a textual rep-

resentation of data and is composed of elements

with hierarchically nested structures as deﬁned in

its corresponding DTD. In our methodology, a doc-

ument is represented by a series of trees T = (e :

val T

··· T

), where T

··· T

are recursively

deﬁned child trees of T , e : val is the root of T and

the parent of T

··· T

, and e ∈ EN, val is a text

string if the root node contains a value, otherwise, it

is omitted. Figure 3 is an example showing an XML

document represented by such trees.

3.3 Hedge and Hedge Conformation

A hedge H is a sequence of trees under one

node in a document. For instance, in the doc-

ument shown in Figure 3, T , T

, T

, and

(title:ABC)(ISBN:-345)(Price:50) are four hedges. A

hedge may contain smaller hedges. Here our in-

terest is in which child trees of a node belong to

a hedge conforming to a speciﬁc type construc-

tor. For example, let g

= [A, [B, C

]

∗

, D

]

, β(e) =

and T =(e((A)(B)(B)(C)(A)(B)(C)(D))), then hedge

(A) conforms to [A], hedge (B)(B)(C) conforms to

[B, C

]

∗

, hedge (A)(B)(B)(C) conforms to g, and hedge

(A)(B)(B)(C)(A)(B)(C)(D) conforms to g

. A hedge H

conforms to g is denoted by H

By using the hedge notation, the child trees of a

node can be logically split and thus, the cardinality

constraints of a structure can be checked.

<root>

<publ>

<article><title>FGH</title><journal>J1</journal><issue>2</issue><page>55-58

</page></article>

<article><title>T8</title><journal>J1</journal><issue>2</issue><page>8-15

</page></article>

</publ>

<publ>

</publ>

</root>

( a ) A simplified document example

T = (root: T

)

= ((name: “M. Fox”) (publ: (T

))), T

= ((name: “K. Page”) ··· )

= ((year: “2006”) (book: ···))

= ((year: “2005”) ···), T

= ((year: “2004”) ···)

······

( b ) The document trees for the example

Figure 3: A document example and its tree expression.

4 XML DATA

TRANSFORMATION

OPERATIONS

In the proposed methodology, the transformation of

XML data is implemented through executing a series

of data transformation operations against the tuple ex-

pression and the document trees. The data transfor-

mation operations are deﬁned by a set of operators.

Because of the syntax differences between DTD and

document, each operator has deﬁned two parts: one

for transforming the DTD and the other for transform-

ing its conforming documents. The formal deﬁnition

of each operator has been presented in (Liu et al.,

2006). This section will provide an overall descrip-

tion of the data transformation operations deﬁned by

those operators.

The DTD transformation operation that each opera-

tor performs is listed in Table 1. Because the doc-

ument transformation operation of each operator is

to convert a given document into one with a struc-

ture that conforms to the transformed DTD, the ta-

ble also reveals the information for what transfor-

mation operation will be carried out on the con-

forming document by each operator. For instance,

unnest operator converts the DTD β(e) = [g

, g

]

into a new DTD β

(e) = [g

, g

]

. The operator

also transforms the document by converting the hedge

AN IMPLEMENTATION OF XML DATA INTEGRATION

113

Table 1: The DTD transformation operation of each opera-

tor.

Operator DTD transformation operations

opin opin([g

, ·· · , g

]

) −→ [g

, ·· · , g

]

c?

where c ⊇?

opout opout([g

, ·· · , g

]

) −→ [g

?

, ·· · , g

?

]

where i = 1, ··· , n(c

⊇?)

min(c

, i, [g

|·· · |g

]

) −→ g = [g

min |·· · |g

|·· · |g

]

cc

, where c ⊇ c

and if i = 0:

∀ j = 1, · ·· , n(c

= c

); else i ∈ [1, ··· , n]:

= c

∧ ∀ j 6= i(c

= c

)

mout(c

, i, [g

|·· · |g

]

) −→ g = [g

··· |g

|·· · |g

]

, where if i = 0 : j = 1, ··· , n

mout (c

⊇ c

∧ c

= c

 c

); else i ∈ [1, ··· , n]:

⊇ c

∧ c

= c

 c

and ∀ j 6= i(c

= c

)

rename rename(e, e

) −→ e

, where e

6∈ parent(e)

shi ft Let g = g

, g

, shift(g

, g

) −→ g = (g

, g

)

group group(g) −→ [g]

ungroup ungroup([g]

) −→ g

expand Let g

∈ g ∧ e 6∈ parent(g

), then

expand(g

, e) −→ g = e ∧ β(e) = g

collapse Let g

= e

∧ β(e) = [g

]

and g

∩ parent(e) = φ

then collapse(e) −→ g

= [g

]

nest Let g = [g

, g

]

∧ c ⊇ +,

nest(g

) −→ g = [g

, g

]

unnest Let g = [g

, g

]

∧ c

= +|∗,

unnest(g

) −→ g = [g

, g

+

]

f act Let g = [[g

, g

]

|·· · |[g

, g

]

, then

fact(g

) −→ g = [g

, [[g

]

|·· · |[g

]

de f act Let g = [g

, [[g

]

|·· · |[g

]

, then

defact(g

) −→ g = [[g

, g

]

|·· · |[g

, g

]

Let g

= e

, ·· · , e

and g

= ¯e

¯c

, ·· · , ¯e

¯c

merg where ∀ i = 1, · · · , m(β(e

) = β( ¯e

)),

then merg(g

, g

) −→ [e

¯c

× ·· · ×e

¯c

]

Let g

= [e

, ·· · , e

]

, c = ∗|+, then split(g) −→

¯c

, g

¯c

, ·· · , g

¯c

, where h ≥ 2 and ¯c

= c  +, ¯c

split = · · · = ¯c

h−1

=?, ¯c

= ∗ and g

= [e

, ·· · , e

= [e

, ·· · , e

], ··· , g

= [e

, ·· · , e

] and

∀ i = 1, · · · , m(e

= e

∧ ∀ j = 2, ·· · , h(β(e

i j

) =

β(e

))) and all e

i j

(i = 1, ··· , m; j = 2, ···h) are

distinct and are not in parent(g)

Let g = [e

, ·· · , e

]

, f = [ ¯e

¯c

, ·· · , ¯e

¯c

]

∀ e

∈ g(β(e

) = Str), ∀ ¯e

∈ f (β( ¯e

) = Str),

pro j c

, ·· · , c

, ¯c

, ·· · , ¯c

∈ [1, ?], c

⊇c

and ∀ ¯e

¯c

∈

f ( j = 1, · · · , w)( if ∃ e

∈ g so that e

= ¯e

then

¯c

⊇c

, else ¯c

=?), then proj(g, f ) −→ f

··· H

which conforms to β(e) into a hedge

··· H

that conforms to β

(e).

The operations that transform a DTD and its conform-

ing documents into a target schema from its original

schema progress in two recognized phases. In the ﬁrst

phase, the XML data is converted into a ﬂat form;

and in the second phase, the ﬂat form is converted

into the target schema. A ﬂat form is deﬁned by

β(e) = [g

|··· |g

]

, where n ≥ 1 and ∀i = 1, · · · , n(c

1|? ∧ g

= [e

, ··· , e

]), ∀ j = 1, ··· , m

i j

∈ EN ∧ c

i j

1|? ∧ β(e

i j

) = Str). Obviously such a ﬂat form has the

minimum layers of brackets to keep the semantics of

disjunctions and conjunctions. It can help to simplify

the comparison of two data schemas. Here the idea is

to respectively convert the original schema β

(e) and

the target schema β

(e) into the ﬂat form B

(e) and

(e), and then convert B

(e) into B

(e) through a se-

ries of projection operations. Suppose the operation

sequence from β

(e) to B

(e) is Φ, then carry out the

revered sequence Φ

−1

against B

(e) to convert it into

an equivalent schema β

(e). By this process, β

(e)

is converted to β

(e), which agrees with the structure

deﬁned in β

(e). Note all the operations in Φ

−1

are

respectively the inverse operations in Φ, e.g., if min

is executed in Φ, then the corresponding operation is

mout in Φ

−1

5 IMPLEMENTATION OF THE

XML DATA

TRANSFORMATION

OPERATIONS

5.1 Main Challenges

There are a number of challenges in the development

of the XML data transformation operators when is-

sues such as information preservation, nested brack-

ets, and mutually nested conjunction and disjunction

are considered. Obviously these issues must be ade-

quately addressed for practical enterprise information

integration applications.

It is essential to preserve the semantics of data

when carrying out a data transformation. The rela-

tionships between data elements must be preserved.

For example, before and after a data transformation,

it is desired that the title and ISBN of a book are put

under the same element. This derives a requirement

that the data transformation operations must be able

to be reversed. Although our operators have been de-

ﬁned by carefully considering this requirement, it is

very complicated to realize the reverse due to the con-

sideration of the full XML syntax. As an example, let

(e) = [g

]

∗

, if we do min(?, 0, [g

]

∗

), we’ll get

(e) = [g

]

∗?

, that is [g

]

because ?? =? and

∗? = +. Clearly we cannot go back to the origi-

nal β

(e) by doing mout(?, 0, [g

]

) because in that

case, we attain β

(e) = [g

]

∗

. A solution to such

problems is not to carry out the multiplicity opera-

tion immediately but just keep the information. That

means we should store the operation ?? attached to g

in the β

(e) in a particular data structure, rather than

getting their operation result immediately. This leads

to the data structure and the algorithm implementing

the operations more complicated.

5.2 Overall Implementation

Framework

The overall framework for implementing a data trans-

formation operator can be brieﬂy described as fol-

lows. Based on the element e to be operated, the β(e)

ICEIS 2008 - International Conference on Enterprise Information Systems

114

is located from the tuple expression built from a given

DTD, and then its output part is updated. This real-

izes the conversion from β(e) to β

(e), the latter will

determine the transformed DTD of the operator. The

β(e) is also provided for the document transforma-

tion. The node e in the document is found through

parsing the document tree, then all the hedges con-

forming to β(e) under the node are converted into

the new ones conforming to β

(e). The conversion

requires considerable complicated operations against

the hedges, including comparison, group, modiﬁca-

tion, re-structure, etc.

5.3 The Implementation of Document

Transformation

To transform a document from its original schema

into a targeted one by using our operators, ﬁve tasks

must be performed: 1) construct document trees from

the given XML ﬁle; 2) locate the nodes to be operated

in the document trees; 3) identify the hedges requir-

ing conversion under each of the nodes; 4) transform

the hedges into a new format according to the opera-

tor; and 5) store the modiﬁed document trees into an

XML ﬁle.

Some of the tasks can be accomplished with the

help of the XML DOM parser (Maruyama, 2002). It

is invoked to traverse the document tree, and when

the node e to be operated is found, it transmits all its

child trees to a procedure. The latter identiﬁes the

hedges that conform to the β(e) provided by the DTD

transformation. If such a hedge is identiﬁed, then task

4 will start and the hedge will be converted according

to the deﬁnition of the operator. At the last, an XML

ﬁle is built by storing the new hedges to it, which can

be accomplished by the parser.

An algorithm has been developed to identify the

hedges that conform to a particular type deﬁnition

from the child trees of a node. It splits the child trees

into logic groups using the hedge notations and then

checks their conformation to a given type deﬁnition.

Its input arguments include: 1) a type deﬁnition ex-

pression gg to which the child trees conform; 2) a type

constructor gg

to which the hedges to be identiﬁed

must conform; 3) the child trees of a node; and 4) an

index from which to start the search in the child trees.

In the algorithm, gg is used as the rule to parse the

child trees, gg

is used as the criterion to check if a

hedge is the one to be identiﬁed.

The algorithm produces two indexes as its output.

The elements between them in the child trees form the

hedge identiﬁed by the algorithm. Due to the space

limit, we are not able to provide the algorithm in this

paper. The interested readers can contact us to get it.

6 THE OPERATOR PACKAGE

AND ITS APPLICATIONS FOR

ENTERPRISE INFORMATION

INTEGRATION

To apply the proposed methodology to realize enter-

prise information integration, we have developed a

Complete XML Data Transformation System. Fig-

ure 4 shows its entry interface. From the interface,

users can, across the Internet, perform various data

transformation to realize enterprise information inte-

gration. They can carry out the data transformation

in a step-by-step mode or ask the system to automati-

cally accomplish a series of transformation operations

for them.

Figure 4: The entry interface of the system.

In the following, we will brieﬂy illustrate the appli-

cations of the method in practical enterprise informa-

tion integration via an example. Recently, publica-

tions are no longer just the distribution of the printed

works, e.g. book or journal. They now include vari-

ous electronic media, e.g. CD, web, etc. In different

publishing companies, the publication information is

normally encoded in different XML formats. It thus

requires techniques to integrate these information to-

gether to provide users with publication information

in a uniﬁed format. Suppose an enterprise informa-

tion system adopts the DTD shown in Figure 5 to

provide users with publication information. Note the

headers and the string type #PCDATA of the DTD are

not included in the ﬁgure to save space. Clearly in

order to provide users with publication information

using such a structure, all the relevant publication in-

formation encoded in other formats, including the one

shown in Figures 2 and 3, must be converted to match

the structure.

Our methodology can be used to realize the publica-

tion information integration. The basic process is, by

AN IMPLEMENTATION OF XML DATA INTEGRATION

115

using the data transformation operators, publication

information encoded in other format is converted to a

ﬂat form, and then further converted into an equiva-

lent structure which conforms to the integrated global

schema.

<!ELEMENT root (course,ref*)*>

<!ELEMENT ref (book|article|VCD|videoTape)>

<!ELEMENT book (title,author,publisher,ISBN,ISSN?,year)>

<!ELEMENT article (title,author,source+)>

<!ELEMENT VCD (title,publisher,ISSN)>

<!ELEMENT videoTape (title,publisher,ISSN)>

<!ELEMENT source (URL*|conference|journal)>

<!ELEMENT conference (cname,organizer,venue,time,URL?)>

<!ELEMENT journal (jname,Vol,No?,PG?)>

......

Figure 5: A common global DTD structure.

7 SUMMARY AND FURTHER

WORK

This paper has presented a framework for implement-

ing XML data integration via converting XML data

from different data sources to an integrated global

schema. The representation of DTDs and documents,

and the transforming operations of XML data, de-

ﬁned by a set of operators, have been illustrated. The

implementation of the transformation operations has

been investigated and a package of the operators has

been reported. In the proposed method, the full XML

syntax has been covered, including nested brackets in

element type deﬁnitions, multiplicity constraints at-

tached to those nested brackets, and disjunction, for

which other work has not provided sufﬁcient support.

Using the methodology, the transformed documents

always conform to the transformed DTDs, which is a

property that is not possessed by any query languages

and algebras where users require detailed program-

ming of the transformation procedure. With our work,

users are freed from using complex language syntaxes

and they just need to combine operators for achieving

their desired XML data integration.

Our next work includes the reﬁnement of the oper-

ators and the automated XML data conversion using

the operators according to a sequence of operations

deﬁned based on the mapping between the original

and target schema. The latter is also the one we will

continue to investigate.

REFERENCES

Boag, S., Chamberlin, D., Fernandez, M. F., Florescu, D.,

Robie, J., and Simeon, J. (2007). Xquery 1.0: An

xml query language. 1st International Conference on

Template Production.

Erwig, M. (2003). Toward the automatic derivation of xml

transformations. LNCS 2814 - ER 2003 Workshops

ECOMO, IWCMQ, AOIS, and XSDM Proceedings,

pages 342–354.

Kay, M. (2007). XSL Transformations (XSLT), Version

2.0. http://www.w3.org/TR/xslt20/.

Liu, J., Park, H., Vincent, M., and Liu, C. (2006). A for-

malism of XML Restructuring Operations. LNCS -

ASWC, pages 342–342.

Maruyama, H. (2002). XML and Java: developing Web ap-

plications. Addison-Wesley, Boston, Massachusetts.

Tian, J., Liu, J., Pan, W., Vincent1, M., and Liu, C. (2008).

Performance Analysis and Improvement for Transfor-

mation Operators in XML Data Integration. APWeb

08, pages 214–226.

Zamboulis, L. (2004). Xml data integration by graph re-

structuring. BNCOD, pages 57–71.

ICEIS 2008 - International Conference on Enterprise Information Systems

116