ODDI
A Framework for Semi-automatic Data Integration
Paolo Ceravolo, Ernesto Damiani, Marcello Leida
Universit
`
a degli studi di Milano, Dipartimento di Tecnologie dell’Informazione
via Bramante, 65, 26013 Crema (CR), Italy
Zhan Cui, Alex Gusmini
Intelligent Systems Research Centre, BT Group, Orion Building - Adastral Park - Martlesham Heath
IP5 3RE Ipswich - Suffolk, U.K.
Keywords:
Data Integration, Mapping Generation, Matching Operators, Clustering, Semantic, Formal Concept Analysis.
Abstract:
Recent works on Business Intelligence do highlight the need of on-time, trustable and sound data access
systems. Moreover the application of these systems in a flexible and dynamic environment requires for an
approach based on automatic procedures that can provide reliable results.
A crucial factor for any automatic data integration system is the matching process. Different categories of
matching operators carry different semantics. For this reason combining them in a single algorithm is a non
trivial process that have to take into account a variety of options.
This paper proposes a solution based on a categorization of matching operators that allow to group similar
attributes on a semantic rich form. This way we define all the information need in order to create a mapping.
Then Mapping Generation is activated only on those set of elements that can be queried without violating any
integrity constraints on data.
1 INTRODUCTION
Data Integration is becoming a relevant problem in
applications that needs to access, analyse and display
data coming from heterogeneous data sources.
In principle Data Integration can be done by a pro-
cedural approach, i.e. creating an ad-hoc integration
with respect to a set of predefined needs, such as in
(Hammer et al., 1995). But, when the queries to be
applied on the sources cannot be define a-priori, a
declarative approach is required. Due to flexibility re-
quirements the declarative approach is more diffused,
and here we limit our discussion to it. According to
the declarative approach, we call local schemata (L)
the set of representations referring to local sources,
while the global schema (G) is the representation in-
tegrating the different local sources. Research issues
regarding Data Integration problem can be grouped in
three big clusters: a first cluster of issues focus on
the generation of G that can be either normative, as in
(Braun et al., 2000), or inductive, as in (Hakimpour
and Geppert, 2002). A second cluster of issues fo-
cus on how to represent the mapping between G and
L. Here two main approaches exist. In the Global as
View approch the mapping is provided on G objects
by using a L vocabulary while in the Local as View
approch the mapping is provided on L objects by us-
ing a G vocabulary. In (Lenzerini, 2002) a detailed
discussion underlines how these approaches impact
on application modeling and data reasoning. The last
cluster of issues focuses on the problem of query an-
swering, studying the computational complexity re-
lated to the different solutions, as in (Abiteboul and
Duschka, 1998) or in (Halevy, 2001), and defining
effective algorithms for dealing to it, as for instance
in (Grahne and Mendelzon, 1999) or (Duschka et al.,
2000). These problems cover nearly the totality of
the relevant theoretical aspects involved in Data In-
tegration. Moreover, with the increasing number of
interaction and complexity of relations, human inter-
action is becoming an help that can not be considered
anymore: the mapping must be generated by means
of an automatism providing high level of quality in
the final mapping between the data sources analyzed.
Here outcomes the importance of sound matching op-
erators that can discover semantics relations between
15
Ceravolo P., Damiani E., Leida M., Cui Z. and Gusmini A. (2008).
ODDI - A Framework for Semi-automatic Data Integration.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - DISI, pages 15-24
DOI: 10.5220/0001678000150024
Copyright
c
 SciTePress

elements of the system.
Matching operators are very susceptible to the
data in input, because different operators are tailored
to different data, and no generic matching function
can be designed. For this reason the only way for
implementing a generic Data Integration algorithm is
to support different matching operators. Moreover,
combining them in a single algorithm is a non triv-
ial process that have to take into account a variety of
options.
This paper deals with the problem of managing
a pallet of matching operator supporting different se-
mantics. The approach chosen is to combine all the
available association produced by different operators
in a cluster. This cluster collect all the elements that
can be associated and express the semantics of the as-
sociations. This way in the cluster we have all the
information need in order to create a mapping. Also
Mapping Generation is activated only on those set of
elements that can be queried without violating any in-
tegrity constraints. Our system is named Ontology
Driven Data Integration (ODDI), it is based on For-
mal Concept Analysis (FCA)(Ganter et al., 2005) as
searching space in order to discover concept-level re-
lations for Mapping Generation, and uses an ontology
as data access layer. Using an ontology as common
conceptualization brings several benefits but the more
relevant is that due to the sound logic basis it is possi-
ble to perform reasoning task on the knowledge base
such as Consistency Checking and Classification (Cui
et al., 2007).
The paper is structuerd as follows: Section 2 in-
troduces the formally a generic Data Integration Sys-
tem, focusing then to our definition of mapping; then
in Section 3 the matching process is described, pro-
viding initially our formalization and then a catego-
rization of the traditional matching operators. Section
4 describes the mapping generation module, focusing
on the use of FCA as a formalism for representing
the information. The paper is enriched with an exam-
ple of the generation of the FCA lattice starting from
a local schema S and a global schema G. Section 5
concludes the paper, outlining conclusions.
2 DATA INTEGRATION
The system we propose in this paper is based on
Global as View approach (Calvanese et al., 1998), be-
cause the G is given trough an ontology and the map-
ping are constructed by associating to the concepts of
G the set of attributes in L that carry the same infor-
mative value of the attributes of these concepts. For-
mally we can define a data integration system as triple
I =< G, L,M >; where G is the global representation,
L the local set of local representations composed by n
single representations s
1
,s
2
,...,s
n
and M is the map-
ping between L and G. The mapping M is the re-
sult of a complex process taking as input M
t
, a set
of matching relations among the simple elements of
G and L and generating the mapping M defined as
M =< M
p
,M
o
>; where M
p
is a mapping between
objects of the local representation L and the global
representation G (such as for instance concepts in an
ontology or table in a database) and M
o
is a mapping
between elements of L: relations between objects of
the same source schema s
a
in L, such as the typical
primary-key→foreign-key, but also relations between
elements of different source schemas s
i
, s
j
of L that
are semantically related.
In general two data set can be integrated only if
they describe a common set of real world facts. Of
course this common set does not have to cover the
totality of the described facts. In (Parent and Spac-
capietra, 1998), relations between facts described by
different data sets are defined by set relationships. Ac-
tually this approach is partially inappropriate because
the instances of two data sets can describe the same
facts at different detail levels or they can describe dis-
tinct facts to be related in G.
According to our work a mapping between data sets
can be oriented to two distinct goals:
• Composition. In this case some redundant infor-
mation is assumed to be stored in the data sets.
The mapping acts on this redundant information
in order to aggregate new compositions of data
items. In this perspective G contains views that
recompose the data items contained in L in a new
structure.
• Summarization. In this case the information
stored in the data sets can be reduced to a com-
mon type. The mapping expresses the commu-
nality shared by different data items. In this per-
spective G contains views that summarize the data
items contained in L in a more compact represen-
tation.
In principle a mapping can cover both these goals. If
an human agent generate the mapping, she will nat-
urally distinguish between the two cases. But if the
mapping is generated by an algorithm, achieving the
right goal mainly depends on the operator adopted for
matching the data items.
The system that we propose consists of two mod-
ules: the first that generates M
t
, given G and L. The
second module generates M
p
and M
o
, by representing
M
t
as an FCA used as searching space to find seman-
tic relations between elements of G, and L.
ICEIS 2008 - International Conference on Enterprise Information Systems
16

3 MATCHING
Matching (M
t
) is the problem of discovering relations
between elements of two different representations (G
and L in this case). The matching at simple element
level can be defined as a relation:
e
i
s
k
∼
=
δ
e
j
g
Where
∼
=
is a binary relation from the set of the fol-
lowing relations: equality, inclusion and specification
(=, <, ⊂). While δ, associated to
∼
=
, can be a bi-
nary ([0,1]) or a fuzzy value ([0..1]) depending on the
method chosen to implement the matching operator
and represents the strenght of the relation. Then ele-
ments of m
t
are: e
i
s
k
= e
j
g
if the data items carried by
e
i
s
k
satisfy e
j
g
with a sound and complete information
(i.e. name and firstName). Or in case of inclusion
e
i
s
k
< e
i
g
if the data items carried by e
i
s
k
provide a por-
tion of the information required for satisfying e
j
g
(i.e.
street and address). e
i
g
< e
i
s
k
if the data items carried
by e
i
s
k
contain more information than the one required
for satisfying e
j
g
(i.e. street and address). Or, in case
of specification, e
i
s
k
⊂ e
i
g
if the data items carried by
e
i
s
k
satisfy e
j
g
with a sound but more general informa-
tion (i.e. email and contact).
In addition an element e can also be subject of a
transformation, allowing to bring e under the range of
a binary relation. We use ∆ as a symbol for meaning
these transformation. So we can have a matching such
as:
∆e
i
s
k
∼
=
δ
e
i
g
if the information carried by e
i
s
k
allow a transforma-
tion that satisfy the semantics of e
i
g
. As an exam-
ple, if e
i
g
represent the nationality of a person and e
j
s
h
his telephone number, we can derive, using a pattern
based operator, the nationality from the international
prefix of the telephone number.
The values
∼
=
and δ are the output of a matching
function φ(e
i
s
k
,e
j
s
h
) that evaluates the semantic rela-
tions between two elements e
i
s
k
and e
j
s
h
.
A variety of methods for implementing the match-
ing function φ were proposed in the literature in order
to define correspondences among elements belonging
to different representations.
The most exhaustive and theorically grounded sur-
vey in this field is (Rahm and Bernstein, 2001), where
a classification of the most traditional methods is pro-
vided. Another important classification is (Euzenat
and Shvaiko, 2007) where semantic aware matching
operators are also considered.
This classification can be organized differentiating
the approaches on the basis of some matching criteria.
The combination of these criteria allows to describe
all the possible approaches for matching function φ.
We can divide the criteria used to define the matching
function in two big groups, according to the informa-
tion item that is considered:
• Schema level: In this case the matching is derived
on the basis of the metadata describing the ele-
ments of the representations analyzed. It can con-
sider only the element itself or an element accord-
ing to its position in a structure. Often this criteria
lacks on providing semantic information because
the meta-data itself could not provide enought in-
formation to the system to associate a semantics
to the element. For example consider dateA and
dateB in a table Product representing respectively
shipping date and expiring date of a product. It
is intuitive to understand that the information pro-
vided only by meta-data in not sufficient.
• Instance level: In this case the matching is per-
formed by comparing the data contained in the el-
ements. Analysing the data, we can obtain more
information associated to the elements considered
that can be used to provide semantics to the ele-
ments. Following the example of Shipping Date
and Expiring Date analysing the instances we dis-
cover that DateA is always before DateB and,
if we modeled this constrain in the ontology, is
easy to associate the right element from the local
source L to the element of the global source G.
an additional categorization of the approaches can be
defined, according to the method used to compare the
elements:
• Element based: Only a single element is taken
into account.
• Structural based: An element is analyzed in rela-
tion to the elements having a given structural clo-
sure to it (i.e. Tables, Data Sources, Foreign Keys,
elements in the same table, etc.).
• Language based: Many techniques are based on a
linguistic approach, evaluating the linguistic clo-
sure among names and textual descriptions of el-
ements.
• Constraint based: Other techniques evaluate the
closure among elements on the basis of con-
straints such as keys and relationships.
The matching process developed in our system sup-
port several matching approaches providing a reach
pallet of semantically different operators. The results
of the different operators finally needs to be combined
somehow by a merging function.
ODDI - A Framework for Semi-automatic Data Integration
17

3.1 Identifier Constraints and Attribute
Relations
After the generation of M
t
, to complete the mapping
it is necessary to generate also the two sets M
p
and
M
o
. As defined in section 2, M
o
is the mapping oc-
curring between elements in the local schema L; these
relations can be derived from a set of Identifier Con-
straint(IC): a group of matching relations from M
t
,
related each other by means of Boolean operators ∨
and ∧. For example we consider the ontology in fig.
1 as global schema G and the three data sources rep-
resented in fig. 2 as local schema L. Let’s assume that
the concepts in the global schema contain the follow-
ing attributes:
Customer =







FullName,
Address,
Contact,
FiscalCode







Employee =

FullName,Address,Contact

RepairOperation =











Date,
StartingTime,
EndingTime,
Type,
CustomerSatis f action











Figure 1: A simple ontology used for our example.
Ah-hoc wrappers are used extract all the useful infor-
mation about the elements in the two schemas G and
L. We consider as elements the columns of the tables
in L and the attributes of the concepts in G. The in-
formation provided by the wrappers are: name, type,
belonging table or concept, belonging schema and all
the available relations between elements.
The matching function analyses the elements ex-
tracted and generates the relations reported in table
1. The ∆, in the example, is a pattern-based opera-
tor used to discover the country (international prefix)
and the province (district number) of a Costumer or
an Office.
As considered previously, wrappers provide also
information about referential integrity constrains ex-
tracted from the local sources L. The ∧ operator is
used to relate the elements, because it is important to
consider all the relations discovered to generate the
IC.
In the example in fig. 2 there are two referential
integrities that can be extracted from the data base
meta-data:
REL DB1 =





O f f iceCode
O f f ice
DS1
∧
O f f iceCode
Empl oyee
DS1





(IC1)
REL DB3 =





OperationID
RepairOperation
DS3
∧
OperationID
CostumerSatis f action
DS3





(IC2)
To compete the set of IC we need to consider also the
semantic relations relating elements belonging to dif-
ferent local representations. We named semantic rela-
tions those relations among tables of different sources
that carry the same informative value and this way al-
low to generate virtual join among tables. We gener-
ate these ICs considering the matching relations from
M
t
that refer to elements of the local schema, connect-
ing the relations using the ∧ operator.
SEM REL 1 =



CostumerNumber
Costumers
DS1
∧
CostumerID
CostumerSatis f action
DS3



(IC3)
SEM REL 2 =





Department
Department
DS2
∧
O f f iceCode
O f f ice
DS1





(IC4)
SEM REL 3 =





EmployeeNumber
Empl oyee
DS1
∧
Technician
RepairOperation
DS3





(IC5)
SEM REL 4 =



FirstName
Empl oyee
DS1
∧
ContactFirstName
Costumer
DS1



(IC6)
SEM REL 5 =



LastName
Empl oyee
DS1
∧
ContactLastName
Costumer
DS1



(IC7)
Once the set of IC is generated the next step is to
discover the relations between elements of the global
schema G and elements of the local schema L we call
this relations Attribute Relation (AR). Considering al-
ways the elements of the set M
t
, for each element in
the global schema G, an AR is a binary relation (= or
<) with the elements form L that the matching process
considers similar. If more than one element from L
ICEIS 2008 - International Conference on Enterprise Information Systems
18

Figure 2: The Data Sources used for our example and the relations between them.
Table 1: List of matching relations between meta-data elements in the example, here are listed also the semantic relations
between data sources.
FirstName
Employee
DS1
= ContactFirstName
Customer
DS1
LastName
Employee
DS1
= ContactLastName
Customer
DS1
O f f iceCode
O f f ice
DS1
= Department
Department
DS2
EmployeeNumber
Employee
DS1
= Technician
RepairOperation
DS3
CustomerNumber
Customer
DS1
= CustomerID
CustomerSatis f action
DS3
FullName
Employee/Customer
Onto
= CustomerName
Customer
DB1
Phone
Customer
DS1
= TelePhone
O f f ice
DS1
Task
Employee
Onto
= Task
Department
DB2
Date
RepairOperation
Onto
= Date
RepairOperation
DB3
Start
RepairOperation
Onto
= Start
RepairOperation
DB3
End
RepairOperation
Onto
= End
RepairOperation
DB3
Type
RepairOperation
Onto
= Type
RepairOperation
DB3
Satis f actionLevel
RepairOperation
Onto
= CustomerSatis f action
CustomerSatis f action
DB3
FirstName
Employee
DS1
< CustomerName
Customer
DS1
LastName
Employee
DS1
< CustomerName
Customer
DS1
FirstName
Employee
DS1
< FullName
Employee/Customer
Onto
LastName
Employee
DS1
< FullName
Employee/Customer
Onto
AddressLine1
Customer
DS1
< Address
Employee/Customer
Onto
AddressLine2
Customer
DS1
< Address
Employee/Customer
Onto
Street
O f f ice
DS1
< Address
Employee/Customer
Onto
City
O f f ice
DS1
< Address
Employee/Customer
Onto
PostalCode
O f f ice
DS1
< Address
Employee/Customer
Onto
Phone
Customer
DS1
⊂ Contact
Employee/Customer
Onto
Email
Employee
DS1
⊂ Contact
Employee/Customer
Onto
TelePhone
O f f ice
DS1
⊂ Contact
Employee/Customer
Onto
∆(TelePhone
O f f ice
DS1
) < Address
Employee/Customer
Onto
∆(Phone
Customer
DS1
) < Address
Employee/Customer
Onto
ODDI - A Framework for Semi-automatic Data Integration
19

can be associated to the element in G we relate by the
∧ operator the elements from L belonging to the same
table or belonging to tables related by an IC. Then we
relate these groups using the ∨ operator. In case of
relations of type ⊂ the elements in AR are related us-
ing the only ∨ operator. Referring to the example the
relations generated are reported in table 2.
Referring to table 1 is possible to see that the el-
ement FiscalCode
Customer
ONT O
is not present and then a
relation can not be generated, so we can presume that
this information is missing in the local schema. Any-
way it is possible to overcome this limit assuming that
the value of this element is defined as the output of a
function Fc with fullname, birthplace, birthdate and
sex as arguments. This function can not be defined
automatically by the system for this reason it is de-
fined externally (for example as a Java class) and the
system refers to it by an annotation on the element
FiscalCode
Customer
ONT O
.
This way we can generate the AR for the miss-
ing attribute. Analysing the annotation we extract the
names of the arguments and by applying the matching
function with the elements of the local schema L we
discover new matching relations that can be used as
arguments of the function Fc. With the new match-
ing relations it is possible to define the AR related to
FiscalCode:
FiscalCode
Customer
ONT O
= Fc






CustomerName
Customer
DS1
DateO f Birth
Customer
DS1
PlaceO f Birth
Customer
DS1
Sex
Customer
DS1






(AR10)
The ICs and the ARs are then used as fundamental
information to generate the Formal Concept Analysis
lattice used to generate the remaining mappings M
o
and M
p
.
4 MAPPING
The goal of a mapping is to relate elements having
the same informative value in the different represen-
tations analyzed.
According to section 2 a mapping can follow the
procedural or the declarative approach. This second
approach is more flexible because it allows to act on
the mapping information during the query processing
phase and it can be used to summarize or compose
elements of the schemas G and L.
A mapping relation is then a relation between en-
tities of type 1:1, 1:n, m:1 or n:m. For instance
given a set of elements {e
1
s
a
,e
2
s
a
...e
n
s
m
} belonging to
a representation s
a
,...,s
n
in L and a set of elements
{e
1
g
,e
2
g
,...e
n
g
} belonging to a representation G, a map-
ping can relate the elements such as for instance,
e
k
g
→ e
1
s
a
ψe
1
s
b
ψ...ψe
n
s
m
in a GaV fashion and e
i
s
j
→
e
1
g
ψe
2
g
ψ...ψe
n
g
} in a LaV fashion.
Where ψ represents an arbitrary constrain that can
range from set-theoretic operators (∩,∪, ...) to more
complex combination e
k
g
→ φ(T ) where φ is an arbi-
trary formula that combines the arguments and T is
a series defined as T = {e
1
s
a
,e
2
s
a
φe
5
s
c
,e
1
s
b
φe
2
s
b
,...,e
n
s
m
}
Referring to section 3.1. AR10 is an example of com-
position.
Following an all-in-one fashion we exploit the
searching space given by modeling our information
as an FCA lattice, processing the lattice to generate
the set of mapping M
p
and the relations M
o
for the
elements involved in the mapping.
4.1 FCA-based Mapping Generation
The mapping generation process is based on Formal
Concept Analysis (FCA) (Ganter et al., 2005) to dis-
cover relations between objects (O
i
s
n
and O
j
g
) of the
two schemas L and G.
FCA has strong mathematical foundations; it is a
branch of lattice theory and its goal is to generate a
lattice representing the relations between objects and
attributes. The relations between the objects and the
attributes are modeled using a formalism called FCA
Context.
An FCA context can be represented as a matrix
with objects (rows) and attributes (columns), the ma-
trix is used to model relations between objects and at-
tributes: where a relation exists a true Boolean value
is inserted in the respective cell, a false value other-
wise.
Given an FCA context ℜ as described above we
can define it as a triple ℜ =< O,A, R > where O =
o
1
,o
2
,...,o
n
are the set of objects, A = a
1
,a
2
,...,a
m
the set of attributes and R the set of relations r
(x,y)
=
o
x
 a
y
between elements of A and O defined as:
o
x
 a
y
=

true if a
y
is an attribute of o
x
f alse otherwise
A formal concept in the concept lattice is defined to
be a pair (O
i
, A
i
) such that: (i) O
i
⊆ O; (ii) A
i
⊆ A;
(iii) every object in O
i
has every attribute in A
i
; (iv)
for every object o
x
in O that is not in O
i
, there is an
attribute a
y
in A
i
that the object does not have; (v) for
every attribute a
x
in A that is not in A
i
, there is an
object o
y
in O
i
that does not have that attribute. O
i
is
called the extent of the concept, A
i
the intent.
These concepts can be partially ordered by inclu-
sion: if (O
i
,A
i
) and (O
j
,A
j
) are concepts, we define
a partial order ≤ by saying that (O
i
,A
i
) ≤ (O
j
,A
j
)
ICEIS 2008 - International Conference on Enterprise Information Systems
20

Table 2: List of Attribute Relations (AR) relating elements from the local schemas L to elements of the global schema G.
Task
Employee
ONT O
=
n
Task
Department
DS2
o
(AR1)
Type
RepairOperation
ONT O
=
n
Type
RepairOperation
DS3
o
(AR2)
CustomerSatis f action
RepairOperation
ONT O
=
n
Satis f actionLevel
CostumerSatis f action
DS3
o
(AR3)
Date
RepairOperation
ONT O
=
n
Date
RepairOperation
DS3
o
(AR4)
StartingTime
RepairOperation
ONT O
=
n
StartingTime
RepairOperation
DS3
o
(AR5)
EndingTime
RepairOperation
ONT O
=
n
StartingTime
RepairOperation
DS3
o
(AR6)
Fullname
Employee/Customer
ONT O
=











CustomerName
Customer
DS1
∨
(FirstName
Employee
DS1
∧ LastName
Employee
DS1
)
∨
(ContactLastName
Costumer
DS1
∧ContactFirstName
Costumer
DS1
)











(AR7)
Contact
Employee/Customer
ONT O
=











TelePhone
O f f ice
DS1
∨
Email
Employee
DS1
∨
Phone
Customer
DS1











(AR8)
Address
Employee/Customer
ONT O
=















(AddressLine1
Customer
DS1
∧ AddressLine2
Customer
DS1
∧
∆(Phone
Customer
DS1
))
∨
(Street
O f f ice
DS1
∧City
O f f ice
DS1
∧ PostalCode
O f f ice
DS1
∧
∆(TelePhone
O f f ice
DS1
))















(AR9)
whenever O
i
⊆ O
j
. Equivalently, (O
i
,A
i
) ≤ (O
j
,A
j
)
whenever A
j
⊆ A
i
.
In this section we provided just an introduction to
FCA for the sake of clearness. For a more exhaus-
tive theoretically grounded coverage, please refer to
(Ganter et al., 2005).
To generate the FCA lattice we define a set of
clusters generated by the ICs and ARs: a cluster c
i
is defined by all the elements that belong to a rela-
tion ICi or ARi. For example in case of the relation
object referring Fullname
Employee/Customer
ONT O
the corre-
spondent cluster c
i
is defined by:
c
FU LLNAME





















FullName
Employee
ONT O
FullName
Customer
ONT O
CustomerName
Customer
DS1
FirstName
Employee
DS1
LastName
Employee
DS1
ContactLastName
Costumer
DS1
ContactFirstName
Costumer
DS1





















We assume that the attributes A are the clusters
c
1
,c
2
,...,c
n
of the set C and the objects O are the
union of the set of object o
s
n
from s
n
in L (tables in
a data source) and the set of objects o
g
from G (con-
cepts of the ontology).
The mapping process then generates a formal context
ℜ =< O,C,R > where R, the set of relations r
(x,y)
=
o
x
 c
y
is defined as:
o
i
 c
j
=



true if the cluster c
j
contains
an attribute a
k
of o
i
f alse otherwise
Applying lattice theories on ℜ a lattice ℑ is gener-
ated. Figure 3 shows the lattice representation of the
formal context represented in Table 3 generated using
Concept Explorer (http://conexp.sourceforge.net/).
Figure 3: FCA Concept Lattice.
The lattice generated is processed in order to discover
semantic relations between objects o
n
s
from the source
ODDI - A Framework for Semi-automatic Data Integration
21

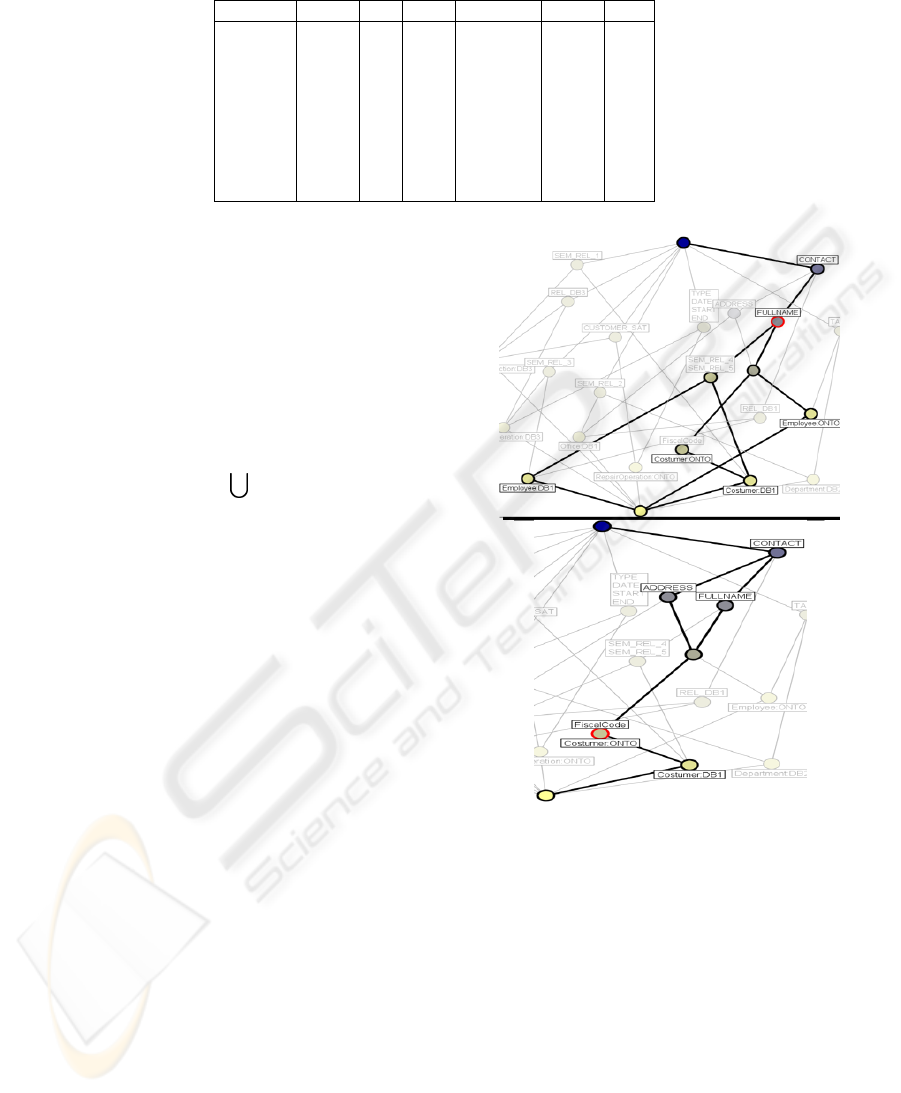
Table 3: The FCA context table.
hunts fly bird mammal swim fish
Lion × ×
Finch × ×
Eagle × × ×
Hare ×
Ostrich ×
Bat × ×
Shark × × ×
Penguin × ×
Whale × ×
schema s
n
in L (the tables of a data source) and the set
of objects o
g
from G (the concepts of the ontology).
The mapping algorithm analyses the FCA concept
lattice and generates, for each objects o
g
of G, a set of
element T
o
g
= {t
e
1
g
,t
e
2
g
,...,t
e
j
g
} where t
e
j
g
is related to
an attribute of a concept of G and is defined as:
t
e
j
g
=< c
k
,W >
with:
c
k
∈ C|∀e
x
g
∈ c
k
∃W =
i=0..m
j=0..n
e
i
s
j
∀e
i
s
j
∈ c
k
Once we generated the clusters, applying the lattice
generation formula to the clusters, our algorithm gen-
erates the FCA lattice showed in fig. 5. This lattice
reports all the information extracted during the match-
ing process and these information are distributed in
a highly structured searching space that will be the
input of out mapping generation algorithm. The lat-
tice is covered by the mapping generation algorithm
in an iterative way, and the use of a FCA as formalism
to represent the information is a sound and strongly
mathematical-based representation that allow to flow
easily between the relations that occur between con-
cepts and elements.
For example, considering the concept
Customer
ONT O
, the first step is to get the intent
of the object to map. Selecting Customer
ONT O
in
the FCA lattice we obtain the set of intents Address,
Fullname, FiscalCode and Contact that refers to the
respective clusters. Now, for each intent considered,
we extract the extent (not considering the elements of
G) that represents the target objects of the selected
intent. Referring to the example in fig. 4 the list of
extents to consider for the intent FullName will be:
T (FullName
Customer
ONT O
) = {Customer
DS1
,Employee
DS1
}
Following the same procedure we obtain the remain-
ing T
i
:
T (Contact
Customer
ONT O
) =



Customer
DS1
,
Employee
DS1
,
O f f ice
DS1



Figure 4: Selecting the object Customer: ONTO the intents
Address, FiscalCode, FullName and Contact are obtained
(above), for each intent the target objects are discovered.
In case of Fullname the extents are Customer:ONTO, Cus-
tomer:DB1, Employee:ONTO and Employee:DB1 (below).
T (Address
Customer
ONT O
) = {Customer
DS1
,O f f ice
DS1
}
T (FiscalCode
Customer
ONT O
) = {Customer
DS1
}
The set T
o
g
of elements T
e
i
g
needs to be semantically
analysed and pruned off from the redundant informa-
tion.
The set T
o
g
is pruned by applying a process that re-
moves from the set T
o
g
the elements that do not share
any equal instance. The algorithms performs a set of
queries and analyse the results to decide which ele-
ments e
s
n
of s
n
in L are not semantically related to
the element e
g
of G. We will avoid the details of the
ICEIS 2008 - International Conference on Enterprise Information Systems
22

Figure 5: The FCA lattice generated from the schemas of
the example.
queries preformed to disambiguate the elements be-
cause the semantic queries are out of the scope of this
paper. After the pruning process the set T
o
g
will be:
T
Customer
ONT O







T (FullName
Customer
ONT O
) = {Customer
DS1
}
T (Contact
Customer
ONT O
) = {Customer
DS1
}
T (Address
Customer
ONT O
) = {Customer
DS1
}
T (FiscalCode
Customer
ONT O
) = {Customer
DS1
}







T
Empl oyee
ONT O













T (FullName
Empl oyee
ONT O
) = {Employee
DS1
}
T (Contact
Empl oyee
ONT O
) =

Employee
DS1
O f f ice
DS1

T (Address
Empl oyee
ONT O
) = {O f f iceDS1}
T (Task
Empl oyee
ONT O
) = {DepartmentDS2}













for the concepts Customer and Employee respectively.
Once the set of T
o
g
is pruned from the redundant infor-
mation it is possible to convert the set in the mappings
M
p
and M
o
. The conversion process is performed
substituting the objects in T
o
g
(the tables of the lo-
cal schemas) with its correspondent in the set of ARs.
Referring to the previous example we obtain the rela-
tions in table 4.
Which is the set of M
p
for the concepts Employee
and Customer. To complete the mapping we need
to generate the set M
o
that is produced according
to the tables involved in the mapping M
p
. Consid-
ering the set of ICs generated previously the set of
M
o
is empty in case of the concept Customer, be-
cause all the attributes are mapped on a single table,
in case of the concept Employee the tables involved
are: Employee
DS1
, O f f ice
DS1
and Department
DS2
and then the set M
o
in this case is composed by all
the ICs that refers to the tables considered in the map-
ping. It is important to underline that all the tables of
the IC need to be present in the mapping. The set M
o
in case of Employee is: M
o
= {(IC1), (IC4)}.
The resulting sets are the mapping M
p
and M
o
that
concludes the mapping generation process. The dis-
covered mapping M needs to be validated: if the map-
ping does not return any result from the query engine
or the query can not be resolved then the mapping is
not considered to be correct, the wrong mapping is
passed in the mapping generation process and an al-
ternative mapping is generated.
5 CONCLUSIONS
This paper addressed the issue of managing a variety
of matching operator in a complex Data Integration
system executing a semiautomatic process. A solu-
tion based on a categorization of matching operators
that allow to group similar attributes on a semantic
rich form. This way we define all the information
need in order to create a mapping. Then Mapping
Generation is activated only on those set of elements
that can be queried without violating any integrity
constraints on data.
The results of the test will be reported in a separate
paper. Several public data sources and the correspon-
dent ontological representation can be found online
and they can be used for an evaluation by compar-
ing the mappings generated by our tool with mapping
generated by a domain expert. This way we can com-
pare our tool with others well known data integration
systems (COMA++, OntoBuilder, Harmony, Mafra)
by exploiting classical Information Retrieval quality
measures such as Precision and Recall. Moreover,
the matching process is a key factor for the quality of
the final mapping, then we performed an additional
evaluation based on the benchmark test of the On-
tology Alignment Evaluation Initiative contest 2007
(OAEI, http://oaei.ontologymatching.org/). The use
of an OWA aggregator in the matching process re-
vealed the limits of this approach during this last test.
An OWA aggregator is not decisional and furthermore
we need a method that is capable to consider also
the semantic of different matching operators. Future
work will focus on the use of logic based decisional
process that will build a knowledge base starting from
the results of the matching operators and will return
the final matching as result of reasoning process over
the knowledge base.
ACKNOWLEDGEMENTS
This work was partly funded by the Italian Ministry of
Research under FIRB contract n. RBNE05FKZ2 004,
TEKNE. This work is also partially supported by
British Telecom (BT) research and venturing.
ODDI - A Framework for Semi-automatic Data Integration
23

Table 4: Mapping relations for the concepts Customer and Employee generated by the FCA-mapping generator.
T
Customer
ONT O













































T (FullName
Customer
ONT O
) = CustomerName
Customer
DS1
T (Contact
Customer
ONT O
) = Phone
Customer
DS1
T (Address
Customer
ONT O
) =








AddressLine1
Customer
DS1
∧
AddressLine2
Customer
DS1
∧
∆(Phone
Customer
DS1
)








T (FiscalCode
Customer
ONT O
) = Fc






CustomerName
Customer
DS1
,
DateO f Birth
Customer
DS1
,
PlaceO f Birth
Customer
DS1
,
Sex
Customer
DS1



















































T
Empl oyeeONTO







































T (FullName
Empl oyee
ONT O
) = (FirstName
Empl oyee
DS1
∧ LastName
Empl oyee
DS1
)
T (Contact
Empl oyee
ONT O
) = (TelePhone
O f f ice
DS1
∨ Email
Empl oyee
DS1
)
T (Address
Empl oyee
ONT O
) =













Street
O f f ice
DS1
∧
City
O f f ice
DS1
∧
PostalCode
O f f ice
DS1
∧
∆(TelePhone
O f f ice
DS1
)













T (Task
Empl oyee
ONT O
) = Task
Department
DS2







































REFERENCES
Abiteboul, S. and Duschka, O. M. (1998). Complexity of
answering queries using materialized views. pages
254–263.
Braun, P., L
¨
otzbeyer, H., Sch
¨
atz, B., and Slotosch, O.
(2000). Consistent integration of formal methods.
In TACAS ’00: Proceedings of the 6th International
Conference on Tools and Algorithms for Construction
and Analysis of Systems, pages 48–62, London, UK.
Springer-Verlag.
Calvanese, D., Lenzerini, M., and Nardi, D. (1998). De-
scription logics for conceptual data modeling. In
Logics for Databases and Information Systems, pages
229–263.
Cui, Z., Damiani, E., and Leida, M. (2007). Benefits of
ontologies in real time data access. In Digital EcoSys-
tems and Technologies Conference, 2007. DEST ’07.
Inaugural IEEE-IES , vol., no., pp.392-397, 21-23
Feb. 2007.
Duschka, O. M., Genesereth, M. R., and Levy, A. Y. (2000).
Recursive query plans for data integration. Journal of
Logic Programming, 43(1):49–73.
Euzenat, J. and Shvaiko, P. (2007). Ontology matching.
Springer-Verlag, Heidelberg (DE).
Ganter, B., Stumme, G., and Wille, R., editors (2005). For-
mal Concept Analysis, Foundations and Applications,
volume 3626 of Lecture Notes in Computer Science.
Springer.
Grahne, G. and Mendelzon, A. O. (1999). Tableau
techniques for querying information sources through
global schemas. Lecture Notes in Computer Science,
1540:332–347.
Hakimpour, F. and Geppert, A. (2002). Global schema gen-
eration using formal ontologies.
Halevy, A. Y. (2001). Answering queries using views:
A survey. VLDB Journal: Very Large Data Bases,
10(4):270–294.
Hammer, J., Garcia-Molina, H., Widom, J., Labio, W., and
Zhuge, Y. (1995). The stanford data warehousing
project. IEEE Quarterly Bulletin on Data Engineer-
ing; Special Issue on Materialized Views and Data
Warehousing, 18(2):41–48.
Lenzerini, M. (2002). Data integration: a theoretical per-
spective. In PODS ’02: Proceedings of the twenty-
first ACM SIGMOD-SIGACT-SIGART symposium on
Principles of database systems, pages 233–246, New
York, NY, USA. ACM Press.
Parent, C. and Spaccapietra, S. (1998). Issues and ap-
proaches of database integration. Commun. ACM,
41(5es):166–178.
Rahm, E. and Bernstein, P. A. (2001). A survey of ap-
proaches to automatic schema matching. VLDB Jour-
nal: Very Large Data Bases, 10(4):334–350.
Yager, R. R. (1988). On ordered weighted averaging ag-
gregation operators in multicriteria decisionmaking.
IEEE Trans. Syst. Man Cybern., 18(1):183–190.
ICEIS 2008 - International Conference on Enterprise Information Systems
24