FORECASTING WITH ARTMAP-IC NEURAL NETWORKS

An Application Using Corporate Bankruptcy Data

Anatoli Nachev

Information Systems, Dept. of Accountancy & Finance, National University of Ireland

Galway, Ireland

Keywords: Financial diagnosis, data mining, neural networks, ARTMAP-IC.

Abstract: Financial diagnosis and prediction of corporate bankruptcy can be viewed as a pattern recognition problem.

This paper proposes a novel approach to solution based on ARTMAP-IC - a general-purpose neural network

system for supervised learning and recognition. For a popular dataset, with proper preprocessing steps, the

model outperforms similar techniques and provides prediction accuracy equal to the best one obtained by a

backpropagation MLPs. An advantage of the proposed model over the MLPs is the short online learning,

fast adaptation to novel patterns and scalability.

1 INTRODUCTION

For a financial institution it important to evaluate

correctly the risk profile of a debtor. Wrong credit

decisions can have important consequences: the

refusal of a good credit can cause the loss of future

profit margins and the approval of a bad credit can

cause the loss of the interests and the principal

money. To estimate credit risk, banks usually apply

scoring systems, which takes into account factors,

such as leverage, earnings, reputation, etc. Due to

lack of metrics and subjectiveness in estimates,

sometimes decisions are unrealistic and not

consistent. Financial research has lead to numerous

studies and a variety of formal techniques for

classification of potential debtors into different

groups in terms of solvency.

1.1 Previous Research

Kumar and Ravi (2007) outline techniques for

financial diagnosis and bankruptcy prediction,

grouped into two broad categories - statistical and

intelligent. The statistical techniques include: linear

discriminant analysis; multivariate discriminate

analysis; quadratic discriminant analysis; logistic

regression (logit); and factor analysis. The group of

intelligent techniques include different types of

neural networks, most popular of which is the multi-

layer perception (MLP); probabilistic neural

networks; auto-associative neural network; self-

organizing map; learning vector quantization;

cascade correlation neural network; decision trees;

case-based reasoning; evolutionary approaches;

rough sets; soft computing (hybrid intelligent

systems); operational research techniques including

linear programming; data envelopment analysis;

quadratic programming; support vector machine;

fuzzy logic techniques, etc.

In their study, (Balcaen and Ooghe, 2004) found

many difficulties in performance of the statistical

techniques due to data anomalies, inappropriate

sample selection, matters related to non-stationarity

and instability of the data, unreasoned faith and trust

on the truth reflected within the financial statements

of the firms under consideration, inappropriate

selection of independent variables and wrong

consideration of the influence of time in the

modelling.

(Zhang et al., 1999) use neural networks to

model bankruptcy prediction and they illustrate links

to traditional Bayesian classification theory. The

study considers initially the five financial ratios

proposed by Altman (1968), joining later on

additional ones. The study also compares the

accuracy of neural networks against that of logistic

regression. The authors suggest that the neural

networks outperform the logistic regression. Atiya

(2001) concluded in his research that, in general, the

neural networks outperform statistical techniques

and suggested to try to improve the predictive ability

of the networks.

This paper proposed a novel approach to bankruptcy

prediction based on the ARTMAP-IC neural

167

Nachev A. (2008).

FORECASTING WITH ARTMAP-IC NEURAL NETWORKS - An Application Using Corporate Bankruptcy Data.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 167-172

DOI: 10.5220/0001680201670172

 SciTePress

networks, a member of the family of neural

networks based on the adaptive resonance theory

(ART). The paper is organized as follows:

Section 1 introduces the bankruptcy prediction

problem and outlines previous research in that area.

Section 2 presents the ART neural networks and

discusses the ARTMAP-IC algorithm and features.

Section 3 describes the experimental data and the

preprocessing steps needed to transform data into a

form proper for submission to the neural network.

Section 4 discusses the experimental results and

outlines advantages of the proposed model.

2 ARTMAP-IC NEURAL

NETWORK CLASSIFIER

In an ART-based network, information reverberates

between the network’s layers. Learning is possible

in the network, when resonance of the neuronal

activity occurs. ART1 was developed to perform

clustering on binary-valued patterns. By

interconnecting two ART1 modules, ARTMAP was

the first ART-based architecture suited for

classification tasks. ARTMAP- IC adds to the basic

ARTMAP system new capabilities designed to solve

the problem with inconsistent cases, which arises in

prediction, where similar input vectors correspond to

cases with different outcomes, (Carpenter,

Grossberg, and Reynolds, 1991), (Carpenter and

Markuzon, 1998). It modifies the ARTMAP search

algorithm to allow the network to encode

inconsistent cases (IC).

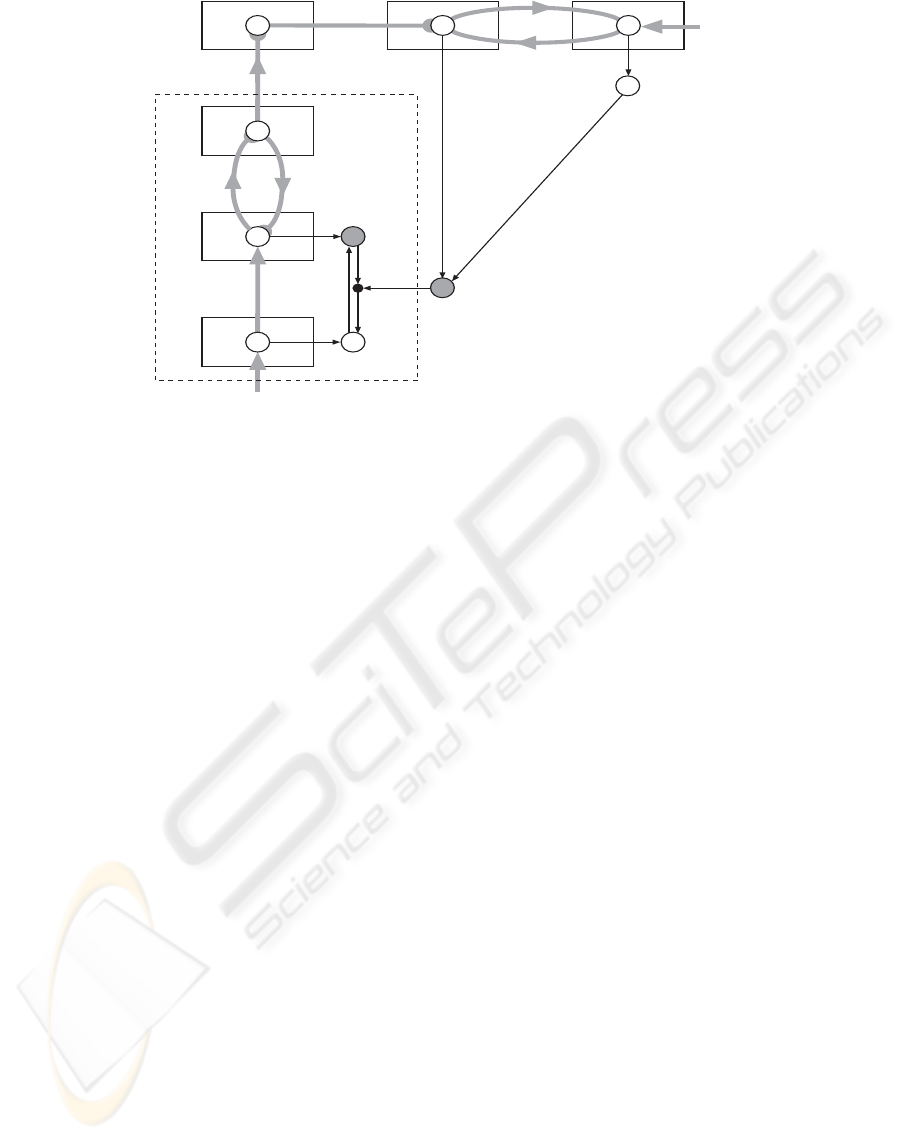
Figure 1, adapted from (Carpenter and

Markuzon, 1998), shows the architecture of an

ARTMAP-IC network. It consist of fully connected

layers of nodes: an M-node input layer F1, an N-

node competitive layer F2, an N-node instance

counting layer F3, an L-node output layer F

, and

an L-node map field F

that links F3 and F

. In

ARTMAP-IC an input a=(a

, a

, … , a

) learns to

predict an outcome b=(b

, b

, …, b

), , where only

one component b

=1, placing the input a in class K.

With fast learning,

=1, ARTMAP-IC represents

category K as hyper-rectangle

ℜ

that just encloses

all the training set patterns a to which it has been

assigned. A set of real weights W={w

: j=1,…,N;

i=1,…,M} is associated with the F1 - F2 layer

connections. Each F2 node j represents a category in

the input space, and stores a prototype vector

=(w

, w

, …,w

). The F2 layer is connected,

through associative links to F3, which in turn is

connected to the map field F

by associative links

with binary weights W

=(w

:j=1,…,N; k=1,…,L}.

The vector w

=(w

, w

, …,w

) relates F2

node j to one of the L output classes. Instance

counting biases distributed predictions according to

the number of training set inputs classified by each

F2 node. During testing the F2->F3 input y

multiplied by the counting weight c

to produce

normalized F3 activity, which projects to the map

field F

for prediction.

2.1 ARTMAP-IC Algorithm

The following algorithm describes the operation of

an ARTMAP-IC classifier in learning mode:

1. Initialisation: Initially, all the neurons of F2

are uncommitted, all weight values w

are initialised

to 1, and all weight values w

of F

are set to 0.

2. Input pattern coding: When a training pair

(a,b) is presented to the network, a undergoes pre-

processing, and yields pattern A=(A

,…,A

). The

vigilance parameter ρ is reset to its baseline value.

3. Prototype selection: Pattern A activates layer

F1 and is propagated through weighted connections

W to layer F2. Activation of each node j in the F2

layer is determined by the choice function

(A)=|A

∧

|/(

+|w

|). The F2 layer produces a

winner-take-all pattern of activity y=(y

,…,y

)

such that only node j=J with the greatest activation

value remains active (y

=1). Node J propagates its

prototype vector w

back onto F1 and the vigilance

test |A

∧

≥ρ

M is performed. This test compares the

degree of match between w

and A to the vigilance

parameter

ρ∈

[0,1]. If this test is satisfied, node J

remains active and resonance is said to occur.

Otherwise, the network inhibits the active F2 node

and searches for another node J that passes the

vigilance test. If such a node does not exist, an

uncommitted F2 node becomes active and

undergoes learning (step 5).

4. Class prediction: Pattern b is fed directly to

the map field F

, while the F2 activity pattern y is

propagated to the map field via associative

connections W

. The latter input activates F

nodes

according to the prediction function

∑

jkj

wyyS

)(

and the most active F

node K yields the class

prediction (K=k(J)). If node K constitutes an

incorrect class prediction, a match tracking signal

raises vigilance just enough to induce another search

among F2 nodes (step 3). This search continues until

either an uncommitted F2 node becomes active

(learning ensues at step 5), or a node J that has

ICEIS 2008 - International Conference on Enterprise Information Systems

168

category

choice

match

input

instance

counting

ART

reset

match

tracking

predictive

error

map field

output

Figure 1: Simplified ARTMAP-IC architecture.

previously learned the correct class prediction K

becomes active.

5. Learning: Learning input a involves updating

prototype vector w

, and if J corresponds to a newly-

committed node, creating a permanent associative

link to F

. A new association between F2 node J

and F

node K (K=k(J)) is learned by setting

=1 for k=K, where K is the target class label for

a. Once the weights (W and W

) have converged for

the training set patterns, ARTMAP can predict a

class label for an input pattern by performing steps

2, 3 and 4 without any testing. A pattern a that

activates node J is predicted to belong to the class

K=k(J)

3 DATA AND PREPROCESSING

For experiments we used data taken from the

Moody's Industrial Manual. The dataset contains

financial information for a number of years for a

total of 129 firms, of which 65 are bankrupt and the

rest are solvent. The data entries have been

randomly divided into two subsets: one for training,

made up of 74 firms, of which 38 bankrupt and 36

non-bankrupt; another set for testing, made up of 55

firms, of which 27 bankrupt and 28 non-bankrupt.

The dataset was used in other studies, e.g.

(Odom and Sharda 1993), (Rahimian et al. 1993),

(Serrano-Cinca 1996), (Wilson and Sharda 1994),

which allows comparing our results with those from

other techniques.

As the raw data contains many features that

describe financial health of firms, it is important to

reduce their number by using few financial ratios, or

variables, instead. Using few variables allows a

prediction technique to reduce the effect of

overfitting and to improve its ability to generalize

and predict. The variables have to be some linear or

nonlinear combinations of features. For our

experiments we adopted the proposed by Altman

(1968) set of five variables, namely:

1) Working Capital / Total Assets (WC/TA). In

general, a firm’s liabilities consist of current

liabilities and long term debt. The current liabilities

include short term loans (less than one year due),

accounts payable, taxes due, etc. The working

capital is current assets minus the current liabilities.

The current assets can or will typically be turned

into money fairly fast. The working capital is an

indication of the ability of the firm to pay its short

term obligations. A firm’s total assets are sum of the

firm’s total liabilities and shareholder equity (capital

raised in share offerings and the retained earnings).

It can be viewed as an indicator of its size and

therefore can be used as a normalizing factor.

2) Retained Earnings / Total Assets (RE/TA).

The retained earnings is the surplus of income

compared to expenses, or total of accumulated

profits since the firm commencement.

3) Earnings Before Interest and Taxes / Total

Assets (EBIT/TA). The firm’s earnings before

interests and taxes is also an important indicator.

Low or negative earnings indicate that the firm is

losing its competitiveness, and that endanger its

survival.

FORECASTING WITH ARTMAP-IC NEURAL NETWORKS - An Application Using Corporate Bankruptcy Data

169

4) Market Capitalization / Total Debt (MC/TD).

Market capitalization relative to the total debt

indicates that a firm is able to issue and sell new

shares in order to meet its liabilities. A large market

capitalization indicates a high capacity to perform

that.

5) Sales / Total Assets (S/TA). Total sales of a

firm, relative to the total assets, is an indicator of the

health of its business, but without certainty as it can

vary a lot from industry to industry.

3.1 Data Preprocessing

A problem with the dataset is that there are

significant differences between the typical variable

values. They differ by several orders of magnitude

due to the different units in which each of these is

expressed. Such an inconsistency would worsen the

prediction accuracy as the variables with large

values would dominate over those with small values.

In our case, the variables MC/TD and S/TA have

larger typical values than WC/TA, RE/TA, and

EBIT/TA. To reduce the effect of the inconsistency

we applied z-score transformation that returns a

centered and scaled version of the datasets. In fact,

the z-scoring returns the deviation of each variable

from its mean, normalized by its standard deviation.

The transformation considers each variable as

independent and uses the formula:

−

where

is the new value,

x is the original one,

∑

−

)(

Another problem with the original dataset or its z-

scored version is that both cannot be used directly as

an ARTMAP-IC input as the input patterns have to

be M-dimensional vectors of floating point numbers

in the interval [0, 1]. The second preprocessing step,

called normalization maps the dataset values into [0,

1] using the formula:

)

(

)

(

minmax

min

−

where

max

and

min

are the max, and min values

of the variable

, respectively. The normalization

additionally reduces the differences between values

preserving the dataset information.

4 EXPERIMENS

The experiments explored how an ARTMAP-IC

performs as a predictor of bankruptcy. The first goal

was to see if a further reduction of the dimensions

would improve the ability to predict and how. The

second goal was to identify the role of the network

parameters. Another goal was to measure the

training and testing times on order to estimate its

efficiency.

A further reduction of the dataset dimensions has

a potential to improve the predictions, as the

Altman’s set of five financial ratios does not

guarantee the best discrimination between the output

classes (solvent / insolvent). This is due to the fact

that a set of variables can overfit or overtrain the

network reducing or destroying its ability to

generalize. There are various techniques to estimate

discriminatory power of variables. Using univariate

F-ratio analysis, Serrano (1996) ranked the Altman’s

ratios and suggested that the second and third

variables have a greater discriminatory power in

contrast to the fifth one. The analysis, however, does

not provide information about the discriminatory

power of combinations of variables and possible

dependencies.

It is also the case that the optimal variable

selection is specific for each particular prediction

technique. There is no guarantee that the optimal set

for one technique would perform well with another.

Ideally, the optimal subset for a model can be found

by the exhaustive search approach that explores each

possible subset. If there are d possible variables,

then since each can be present or absent, we have a

total of 2

possible subsets. The five Altman’s

variables yield thirty one subsets, (all zeroes is

ignored), which is not too much in terms of

possibility to be explored. Taking into account the

above, we decided to adopt the exhaustive search to

analyze the variable subsets and figure 2 shows the

results. Each bar presents a subset. The x axis shows

the subset indexes: 1 to 5 correspond to subsets of

individual variables; 6 to 15 – for pairs of variables;

16 to 25 – for triples; 26 to 30 – quartets; and 31 is

the whole set. Individual sub-bars within a bar

present the prediction accuracies with different

vigilance parameter values from 0 to 1 with an

increment of 0.025. The figure shows that the subset

with highest prediction accuracy is the 11-th one,

which consists of the variables {RE/TA, MC/TD}.

The figure also shows that these two variables are

best individual performers for the ARTMAP-IC (see

bars 2 and 4), so that when joined in a pair, the

resulting subset provides a greater discriminatory

power.

ICEIS 2008 - International Conference on Enterprise Information Systems

170

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 3

subset index

prediction accuracy %

Figure 2: Prediction accuracy of each of the variable

subsets using 41 values of the vigilance parameter.

An additional explanation of this fact can be found

from the correlation matrix of the dataset. If a

correlation value for two variables is close to 0, they

are uncorrelated, or independent, and combined

together provide a greater ability for discrimination

between the classes. The calculations show that the

two variables have correlation 0.11, which is one of

the lowest.

The experiments show that the prediction

accuracy of the 11

subset with certain values of the

vigilance parameter ρ is 83.6% (see figure 3).

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

vigilance parameter value

prediction accuracy %

Figure 3: Prediction accuracy of subset {RE/TA, MC/TD}

varying the vigilance parameter from 0 to 1 with

inclement 0.025.

This accuracy is equal to the best one obtained by an

MLP neural network in (Serrano 1996). Both

techniques used the same dataset. A comparison

between the ATRMAP-IC model and other

prediction techniques that have used the same

dataset can be seen in table 1. The ARTMAP-IC and

Serrano’s MLP misclassify 9 firms, all other

techniques – 10, except the Odom & Sharda’s Liear

Discriminant Analysis, which misclassifies 14.

Another group of experiments aimed to

determine the optimal network parameters. The

results show that regardless of the subset, the

optimal parameter values are: baseline vigilance

parameter ρ

test

=0; signal rule parameter α=0.01; and

learning fraction parameter β=1.0. The vigilance

parameter ρ (Rhobar), which determines the level of

details and granularity of the classes encoded into

the system, has different optimal value for different

subsets. The winning subset obtains best accuracy

with 0≤ρ≤0.4 and 0.5≤ρ≤0.575.

The experiments also showed that the network

training and testing time do not exceed 0.02 sec for

any variable subset and parameters’ values, which is

an indication that the model is efficient and responds

in a real time.

Table 1: Misclassified patterns by the ARTMAP-IC model

(€) and those from other models, all applied to the test

dataset.

# ARTMAP-

Other

studies

# ARTMAP-

Other

studies

* %

8 €

* %

*#%&@$

# @

*#%&@

13 €

17 €

*#%&@$

18 €

*#%&@$

20 €

21 €

#%& $

*#%&@$

*# &@$

24 €

25 €

*#%&@$

#%&@$

28 €

* Misclassified by Odom and Sharda LDA – 14

# Misclassified by Odom and Sharda MLP – 10

% Misclassified by Rahimian et al MLP – 10

& Misclassified by Perceptron Model – 10

@ Misclassified by Athena Model – 10

$ Misclassified by Serrano MLP – 9

€ Misclassified by our ARTMAP-IC – 9

FORECASTING WITH ARTMAP-IC NEURAL NETWORKS - An Application Using Corporate Bankruptcy Data

171

5 CONCLUSIONS

This paper proposes a novel approach to the

bankruptcy prediction problem based on a

supervised ARTMAP-IC neural network. An

advantage of using that type of neural network over

the most popular MLPs is that it provides fast, one-

pass online learning, and it retains already acquired

knowledge while learning from novel patterns. In

contrast, the backpropagation MLP requires

numerous iterations, or epochs, to learn a new

pattern. This makes the ARTMAP-IC model

efficient and scalable for a continuously changing

input space, such as the bankruptcy prediction

domain.

Another advantage of the proposed model is the

high prediction accuracy. Compared with different

techniques over the same experimental data, the

model achieves the highest accuracy obtained by an

MLP, and outperforms all other techniques.

In conclusion, we find that ARTMAP-IC neural

network is suitable for application areas, such as the

financial diagnosis and bankruptcy prediction.

REFERENCES

Altman, E. (1968). Financial Ratios, Discriminant

Analysis, and the Prediction of Corporate Bankruptcy,

Journal of Finance 23(4), 598-609.

Atiya, A. (2001). Bankruptcy Prediction for Credit Risk

Using Neural Networks: A Survey and New Results.

IEEE Transactions of Neural Networks 12(4): 929-

935.

Balcaen, S., and Ooghe, H. (2004). 35 years of studies on

business failure: An overview of the classical

statistical methodologies and their related problems.

Working paper 248, Ghent University, Belgium.

Carpenter, G. A. and Markuzon, N. (1998). ARTMAP-IC

and Medical Diagnosis: Instance Counting and

Inconsistent Cases. Neural Networks, 11(2), 323-336.

Carpenter, G. A., Grossberg, S. and Reynolds, J. H.

(1991). ARTMAP: Supervised Real-Time Learning

and Classification of Nonstationary Data by a Self-

Organizing Neural Network. Neural Networks, 4.

Kumar, P. and Ravi, V. (2007). Bankruptcy Prediction in

Banks and Firms via Statistical and Intelligent

Techniques, European Journal of Operational

Research 180 (1): 1-28.

Odom, M., and Sharda, R. (1993). A Neural Network

Model for Bankruptcy Prediction, in: R.R. Trippi and

E. Turban, Eds., Neural Networks in Finance and

Investing, Probus Publishing Company, Chicago.

Rahimian E., Singh, S., Thammachacote, T., and Virmani,

R. (1993). Bankruptcy prediction by neural networks,

in Neural Networks in Finance and Investing, R.

Trippi and E. Turban, Eds. Chicago: Probus Publ.

Serrano-Cinca, C., (1996). Self organizing neural

networks for financial diagnosis. Decision Support

Systems 17: 227–238.

Wilson, R., and Sharda, R. (1994). Bankruptcy prediction

using neural networks. Decision Support Systems 11:

31–447.

Zhang, G., Hu, M., Patuwo, B., and Indro, D. (1999).

Artificial Neural Networks in Bankruptcy Prediction:

General Famework and Cross-validation Analysis,

European Journal of Operational Research 116, 16 -

32.

ICEIS 2008 - International Conference on Enterprise Information Systems

172