
INCREMENTAL ONTOLOGY INTEGRATION
Thomas Heer, Daniel Retkowitz
Department of Computer Science 3, RWTH Aachen University, Ahornstr. 55, 52074 Aachen, Germany
Bodo Kraft
AMB Generali Informatik Services GmbH, Anton-Kurze-Allee 16, 52064 Aachen, Germany
Keywords:
Knowledge Management, Ontology Engineering, Information Integration Tools, Human Factors.
Abstract:
In many areas of computer science ontologies become more and more important. The use of ontologies for
domain modeling often brings up the issue of ontology integration. The task of merging several ontologies,
covering specific subdomains, into one unified ontology has to be solved. Many approaches for ontology
integration aim at automating the process of ontology alignment. However, a complete automation is not
feasible, and user interaction is always required. Nevertheless, most ontology integration tools offer only very
limited support for the interactive part of the integration process. In this paper, we present a novel approach for
the interactive integration of ontologies. The result of the ontology integration is incrementally updated after
each definition of a correspondence between ontology elements. The user is guided through the ontologies to
be integrated. By restricting the possible user actions, the integrity of all defined correspondences is ensured by
the tool we developed. We evaluated our tool by integrating different regulations concerning building design.
1 INTRODUCTION
Our approach to ontology integration has been devel-
oped in the context of the ConDes research project
(Kraft, 2007). In this project we have developed new
concepts for software tools to support the conceptual
design phase in building design. Thereby a knowledge-
based approach has been followed. The relevant termi-
nology is defined in several domain-specific ontologies.
Based on theses ontologies restrictions for the concep-
tual design of a building can be specified. Because
of this context, the example ontologies in this paper
come from the domain of building engineering, but
our approach for interactive ontology integration is
applicable to many other domains.
There is a broad field of different types of
structures that are all subsumed by the term ontol-
ogy (G
´
omez-P
´
erez et al., 2004). Ontologies can be
simple vocabularies, i. e. lists of terms, which denote
the entities of a certain domain. If a generalization
relation is defined for these terms, one speaks of a
taxonomy. Both of these types are called light-weight
ontologies. Light-weight ontologies define concepts,
classifications of these concepts, properties and rela-
tions. In contrast to that, heavy-weight ontologies com-
prise further semantical information about a domain.
This additional information is specified by axioms or
constraints. Ontologies can describe concepts on dif-
ferent levels of abstraction. Ontologies, which define
general concepts, are called upper ontologies, foun-
dation ontologies, or top-level ontologies (Guarino,
1998). Ontologies, which contain knowledge about a
specific domain, are called domain ontologies.
With regard to ontologies the term integration is
used with several different semantics. Three types of
ontology integration can be distinguished (Pinto et al.,
1999). The first type is integration in terms of reuse.
This means constructing a new ontology based on al-
ready existing ontologies, which are incorporated in
the new ontology. A second type is integration in terms
of merging. In this case, two or more ontologies are
unified into a single ontology by merging correspond-
ing concepts in the original ontologies. The third type
is integration in terms of use. This type of integration
is applied, when applications are built, which are based
on one or more ontologies. In our approach, we use
the term integration in the second sense, i. e. in terms
of merging.
13
Heer T., Retkowitz D. and Kraft B. (2008).
INCREMENTAL ONTOLOGY INTEGRATION.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - ISAS, pages 13-20
DOI: 10.5220/0001680800130020
Copyright
c
SciTePress

Before merging different ontologies into one uni-
fied ontology, a prior alignment of these is required
(Pinto et al., 1999). Alignment is the process, in which
the relations between the concepts contained in the dif-
ferent ontologies are determined. This is usually done
by the definition of a mapping between the ontology
elements. This mapping defines how the source ontolo-
gies have to be merged into one integrated ontology,
so that the resulting ontology contains all the semantic
information of the source ontologies, not more and
not less. One difficulty in the alignment of different
ontologies comes from the fact, that the structure of
an ontology is not only determined by the comprised
knowledge, but also by the design decisions made
during its development. Therefore, even ontologies,
which model the same part of a certain domain, may
be structured significantly different. This makes the
integration of the ontologies a difficult task.
The paper is structured as follows. First, we give
an overview of related work in section 2. Then, in sec-
tion 3, we will describe how to define semantic corre-
spondences and how to generate an integrated ontology
from these correspondences. The following section 4
contains the description of our developed integration
algorithm. Next, in section 5, we describe, how the
integrity of the defined semantic correspondences is
ensured. In section 6, we give a short overview of
the tool we developed to implement the integration
approach. Finally, we give a conclusion and an out-
look on further possible developments at the end of
the paper.
2 RELATED WORK
Ontologies and ontology integration are still emerg-
ing topics in the field of computer sciences. Many
approaches for the use and integration of ontologies
have been proposed in research.
In (Wache et al., 2001) different techniques for
the alignment of ontologies are described. These are
manual definition of correspondences, use of linguistic
heuristics, top-level grounding and the use of seman-
tic correspondences. These techniques are not exclu-
sive, but rather complement each other. The first tech-
nique requires a knowledge engineer, developing an
ontology, to manually define certain correspondences
between the concepts of the ontologies to integrate.
These correspondences mainly have the semantics of
equivalence, but are not restricted to 1:1 relations. In
the second method, heuristics are applied to find corre-
spondences automatically based on linguistic features
of the terms, representing the concepts. The method
of top-level grounding requires a common top-level
ontology for all ontologies to be integrated. This top-
level ontology is then used to identify related concepts,
and to use this information as a basis for the integra-
tion. Finally, semantic correspondences can be defined.
In this method, different types of semantic relations
are used to relate the concepts of the ontologies to
integrate. This way, not only equivalence relations,
but also relations with other semantics can be defined.
In our approach, we use the techniques of top-level
grounding and semantic correspondences.
In (Kalfoglou and Schorlemmer, 2003) and (Eu-
zenat, 2004) surveys over existing approaches to on-
tology alignment are presented. Both works give an
overview over theoretical frameworks and several cur-
rent research projects. The surveyed works range from
formal over heuristic approaches to approaches, which
use machine learning to automate the process of ontol-
ogy alignment. However, most of the presented works
more or less neglect the issues involved with the inter-
active part of the integration process. In the following
we present two examples of related works, which use
heuristics for the alignment of ontologies.
One alternative to align ontologies is, to consider
lexical similarities between the terms, which represent
the defined concepts. Such a lexical integration ap-
proach is implemented by the tool Chimaera (McGui-
ness et al., 2000). Chimaera is an environment, which
can be used for merging and testing ontologies. When
integrating ontologies, Chimaera generates lists of
suggestions for equivalent terms from the ontologies.
These suggestions are based on lexical similarity mea-
sures. Besides that, Chimaera can identify parts of
the class hierarchy, which probably need to be reorga-
nized. These parts are identified by means of heuristic
strategies. Since Chimaera uses heuristics based on
lexical analysis, the identified similarities may contain
mismatches. Thus, it is necessary that the user verifies
all suggestions made by the tool. However, Chimaera
does not propose any solutions in case of conflicts,
which may arise during the integration process.
In (Noy and Musen, 2000), an algorithm for semi-
automatic merging and alignment of ontologies called
PROMPT is presented. This algorithm realizes a
semi-automatic integration of ontologies. The Anchor-
PROMPT algorithm (Noy and Musen, 2001) is an
extension to PROMPT. It is used to generate sugges-
tions, which are not only based on linguistic similarity,
but also on structural properties of the ontologies. In
the first step, PROMPT generates suggestions for cor-
respondences between the classes of the ontologies, to
be integrated. These initial suggestions are based on
linguistic similarities of the class names and the struc-
ture of the ontologies. The latter is analyzed by the
Anchor-PROMPT algorithm. In the next step, the user
ICEIS 2008 - International Conference on Enterprise Information Systems
14

selects for each suggestion an operation to perform or
defines a different operation manually. PROMPT then
automatically performs the selected operation and ap-
plies additional modifications to the merged ontology,
if required. Subsequently, the list of suggestions is
updated and a list of conflicts, which resulted from the
previous operation, is generated. After this, the proce-
dure is executed again, until no more operations have
to be performed, and all suggestions are processed.
In (Hakimpour and Geppert, 2001), ontologies are
used to integrate database schemata. To perform the in-
tegration, the schemata are augmented by correspond-
ing ontologies that define the schema semantics. These
ontologies are then integrated to a global ontology
from which a unified schema can be derived. To in-
tegrate the ontologies, similarity relations between
schema concepts are defined. In (Hakimpour and Gep-
pert, 2001) the same four types of similarity relations
are used as in our ontology integration approach. It is
described, how the resulting integrated ontology can
be derived from the source ontologies and the defined
correspondences. There are different suggestions, how
to define the similarity relations between ontology el-
ements, neither of which is discussed in detail. One
suggestion is, to provide common references by using
a higher level ontology. Other possibilities are, to use
thesauruses, experts familiar with both ontologies, or a
hybrid semiautomatic method. However, no concepts
are proposed, how an expert could be supported in
defining the similarity relations, which includes find-
ing corresponding elements and choosing the right
relation types. Nothing is said about, how to ensure
the integrity of the defined correspondences, and how
to take the effects of defined correspondences on the
integration result into account during the alignment of
the ontologies.
3 SEMANTIC
CORRESPONDENCES
In our approach of merging lightweight ontologies,
semantic correspondences are used to relate the con-
cepts of different ontologies to each other. Following
an interactive incremental process, a knowledge en-
gineer defines correspondences between elements of
the ontologies to be integrated. Based on these cor-
respondences an integrated ontology is automatically
generated.
There are four types of correspondences with dif-
ferent semantics: equivalence, overlap, generalization
and disjointness.
The chosen terms for the semantic correspondence
types overlap and disjoint are rooted in the field of
Ontology 1
Ontology 2Correspondence Extensions
toilets, restrooms
restrooms
ladies
restrooms
hallways corridors
toilets
kitchens
Figure 1: Corresponding concepts and their extensions.
set theory. In our ontology integration scenario, the
elements of ontologies are terms, structured in a gen-
eralization hierarchy. The terms represent concepts.
Hence, correspondences between ontology elements
relate concepts to each other. A concept defines a men-
tal collection of objects or circumstances, which have
common attributes. This collection is called the exten-
sion of the concept (Hakimpour and Geppert, 2001).
Extensions are basically sets. Thus, between two ex-
tensions one of the four possible relationships between
sets must hold. The extensions of two concepts can
be equal or disjoint, one can be a subset of the other,
or the two extensions can overlap, i. e. they have a
nonempty intersection, but are neither equal nor in a
set-subset relation. From these four possible relations
between sets the four correspondence types equiva-
lence, disjoint, generalization and overlap are derived.
In figure 1, examples of corresponding ontology ele-
ments and their extensions are shown. For example the
generalization correspondence from ladies restroom
to restroom implies that the extension of the former
concept is a subset of the extension of the latter con-
cept. Informally speaking, all ladies restrooms are
restrooms. The disjoint correspondence is a special
case insofar as it is not explicitly represented by an
edge between ontology elements. Whenever no cor-
respondence of one of the other three types is defined
between two concepts, they are implicitly defined as
disjoint.
The defined correspondences between ontology el-
ements allow for the automatic generation of a merged
ontology. In our approach an arbitrary number of
source ontologies can be merged into one ontology.
To illustrate this, we consider here the result of the
integration example from section 4. In figure 3 c)
cutouts of three ontologies from the domain of build-
ing construction are shown along with the resulting
merged ontology. Several correspondences are defined
between the elements of the source ontologies, e. g.
the terms toilet and restroom are defined as equivalent.
The terms dining room and living room are defined as
overlapping, since there are rooms that have the func-
tionality of both, like e. g. a family room. Therefore
family room is defined as a specialization of dining
INCREMENTAL ONTOLOGY INTEGRATION
15

room.
During the execution of the integration procedure,
the knowledge engineer selects elements of the merged
ontology to define correspondences, but the correspon-
dences are established between the elements of the
source ontologies or correspondences, which generate
the selected elements of the merged ontology.
The merged ontology is not generated at once, after
all correspondences have been defined. It is incremen-
tally updated throughout the execution of the integra-
tion algorithm, which is described in the following
section.
4 INTEGRATION ALGORITHM
In our integration approach an arbitrary number of
ontologies can be merged into one ontology, which
contains all the semantic information of the source on-
tologies. In the first step two ontologies are integrated.
After that, all remaining ontologies are integrated one
by one into the merged ontology, where each ontol-
ogy is integrated with the current intermediate result.
Except for the choice of terms, which represent the
concepts in the merged ontology, the integration result
is independent of the order, in which the source on-
tologies are integrated. This is guaranteed, because the
correspondences defined throughout the integration
process are established between elements of the origi-
nal source ontologies. The source ontologies remain
unchanged in the knowledge base, and the merged on-
tology can be generated from the source ontologies
and the defined correspondences at any time.
Our ontology integration approach provides so-
lutions to the aforementioned problems. It aims at
providing tool support for the interactive integration
of ontologies. The effects of defined correspondences
are on the one hand taken into account by the fact,
that the knowledge engineer always works with the
current intermediate result. On the other hand, defined
correspondences restrict the possibilities for defining
new correspondences.
The problems of finding corresponding ontology
elements and defining the correspondences in the right
order are addressed by two aspects of our integration
algorithm. First, a restrictive traversing order of the
merged ontology is enforced. And second, those on-
tology elements, for which correspondences can be
defined at a certain point in the integration processes,
are restricted to a manageable number. This way the
knowledge engineer is guided through the merged on-
tology, and his attention is focused to a relatively small
part of the possibly large ontology.
Our integration approach relies on the assumption,
Figure 2: Highlighting of ontology elements.
that all ontologies use a common top-level ontology.
When integrating two ontologies, one can assume that
the roots are equivalent concepts. Thus, in a first step a
top-level grounding of the two ontologies is performed.
After the definition of equivalence correspondences
between the roots of the ontologies, a first version
of the merged ontology is generated. In this merged
ontology the corresponding ontologies are combined
by unifying their roots. After the top-level grounding
an adapted breadth-first traversing is performed. The
traversing is steered by the defined correspondences.
At each point during the integration of two ontolo-
gies some elements are highlighted. The knowledge
engineer is only allowed to define correspondences
between these highlighted elements.
In figure 2 the highlighting of ontology elements
depending on the type of a previously defined cor-
respondence is shown. For example in figure 2 a)
an equivalence correspondence has been established
between the ontology elements A and 1. At a later
point in the integration procedure the knowledge engi-
neer is asked to define correspondences between the
highlighted elements B, C, 2 and 3. In figure 2 b) a
generalization correspondence between A and 1 has
been established. The ontology element A is defined
to be a specialization of 1. Hence, in a later step the
relationships between A and the specializations of 1,
namely 2 and 3, have to be clarified. The case of an
overlap correspondence constitutes a special case. An
overlap correspondence provides the least information
about the relationships of the specializations of the
linked objects. Thus, the highlighting of ontology ele-
ments is conducted in three steps. In a first step, one
of the corresponding elements and the specializations
of the other are highlighted, like it is shown in figure
2 c). In this step it is not allowed, to define equivalence
correspondences between A and either 2 or 3, because
ICEIS 2008 - International Conference on Enterprise Information Systems
16

this would imply, that A is a generalization of 1. For
the same reason it is furthermore not allowed to define
a generalization correspondence with A as source and
one of the specializations of 1 as target. In a second
step the highlighting of the ontology elements is the
other way round as in the first step, while the same
restrictions apply. This situation is depicted in figure
2 d). While in figure 2 c) the case of an overlap corre-
spondence without generation (indicated by the dashed
arrows) of an ontology element is shown, in figure 2
d) the element for the intersection is generated. This
element is not highlighted in steps one and two, be-
cause its relationships to the overlapping concepts are
already defined. Finally, in the third step all special-
izations of the overlapping concepts are highlighted,
including a potentially generated element, to give the
knowledge engineer the opportunity to clarify their
relationships. This situation is not depicted in figure 2.
Figure 3 shows some steps of the integration al-
gorithm by example. Figure 3 a) shows the situation
directly after the top-level grounding of ontology 1
and ontology 2, as explained earlier. The root con-
cepts of the ontologies are linked by an equivalence
correspondence. Hence, the generated merged ontol-
ogy depicted in figure 3 a) on the right contains only
one element room and all specializations of room from
the two ontologies are children of this root element.
The elements sanitary room, toilet and dining room are
highlighted. In the following, the knowledge engineer
defines a generalization correspondence from toilet to
sanitary room. This is the only correspondence, he
defines for the highlighted elements, and thus the algo-
rithm proceeds. Because of the defined generalization
correspondence, in figure 3 b) the ontology elements
restroom and toilet are highlighted. The knowledge
engineer defines an equivalence correspondence be-
tween these elements. In this case, the generalization
correspondence is modified, so that it references the
equivalence correspondence instead of the ontology
element toilet. This is depicted in figure 3 c). Figure 3
c) shows the final situation, in which a third ontology
has been integrated with the other two ontologies. The
resulting merged ontology contains all the semantic
information of the source ontologies.
5 CORRESPONDENCE
INTEGRITY
Many tools for the integration of ontologies generate
suggestions for possible semantic correspondences be-
tween ontology elements, but provide no assistance
for choosing the right correspondences in the right
order. In our view the main functionality of a tool,
which provides support for the alignment of ontolo-
gies, should be, to ensure the integrity of user-defined
semantic correspondences. The integrity is ensured,
if no conflict between defined correspondences exists
regarding their semantics.
In our ontology integration approach, the integrity
of defined correspondences is ensured by several
means. Some of these have already been described
in section 4. The breadth-first traversing order en-
sures, that correspondences between general concepts
of the ontologies are defined before correspondences
between their specializations. The former restrict the
possibilities for defining the latter.
The incremental integration approach reduces the
possibility of defining inconsistent correspondences,
because changes like the unification of equivalent ele-
ments are immediately performed on the merged on-
tology. The highlighting of ontology elements and the
restrictions, which hold for defining correspondences
between them, also contribute to ensuring the integrity
of defined correspondences, as described in section 4.
These restrictions can be seen as static restrictions, as
they do not depend on previously defined correspon-
dences between the highlighted elements and their
generalizations.
However, when defining correspondences between
the highlighted ontology elements, all previously de-
fined correspondences between the highlighted ele-
ments, between their generalizations, and between the
former and the latter have to be taken into account.
Thereby, we consider the type of the correspondence
to be defined as well as the types of previously defined
correspondences. Restrictions, which arise through
this consideration, are called dynamic restrictions. To
determine all dynamic restrictions for a certain corre-
spondence type, we examined the extensions of those
concepts that should be linked by the new correspon-
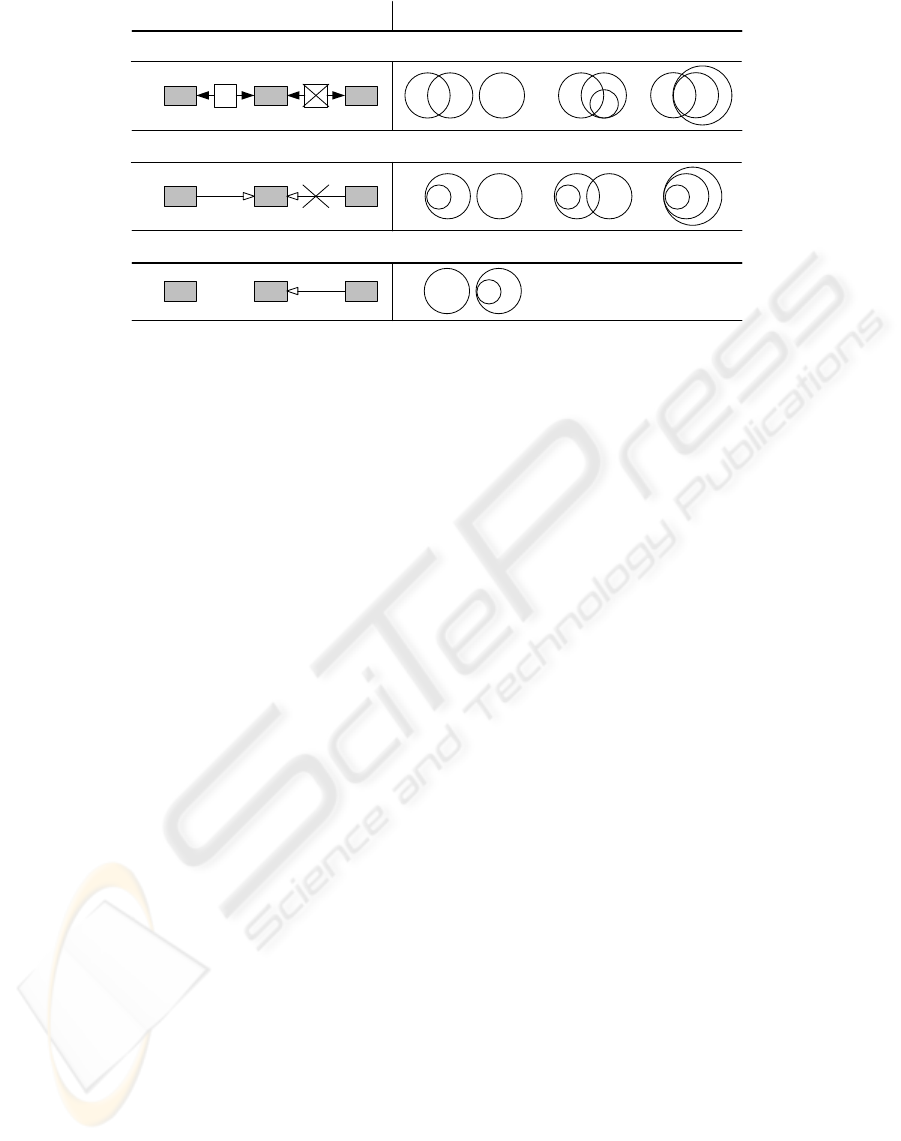
dence. In figure 4 for each correspondence type one
example case is shown, in which the definition of a cor-
respondence is prohibited. The restrictions result from
the relationships of the concepts’ extensions. Crossed
out correspondences mean, that in the defined case
there must not be a correspondence of the given type,
e. g. in figure 4 b) the pattern includes all cases, where
there is no generalization correspondence from S to X.
The example in figure 4 b) is a case in which no
generalization correspondence can be established be-
tween the ontology elements G and S, where G should
be defined as the more general concept and S as its
specialization. The ontology element G is a specializa-
tion of another ontology element X, while S is not. On
the right side, the possible relations between the exten-
sions of G, S and X are shown. The extensions of X and
S can be disjoint, they can overlap, or the extension of
INCREMENTAL ONTOLOGY INTEGRATION
17

Ontology 1 Ontology 2 Ontology 3 Merged ontology
a)
b)
c)
dining room
room
sanitary room
restroom
room
toilet
e
g dining roomsanitary room
restroom
room
room
living room
family room
dining room o
g
room
sanitary room
restroom
room
toilet
e
g
e
living room
family room
dining roomsanitary room
restroom
room
dining room
room
sanitary room
restroom
room
toilet
e
dining roomsanitary room
restroom
room
toilet
toilet
Figure 3: Example steps of the integration procedure.
X can be a subset of the extension of S. However, in
any case it is impossible, that the extension of S is a
subset of the extension of G. Hence, a generalization
correspondence from S to G is not allowed.
The fewest restrictions apply for the definition of
an overlap correspondence, because it provides the
least information about the relation of the linked con-
cepts, and is thus compatible with most other corre-
spondences.
Whenever a knowledge engineer is going to de-
fine a new correspondence, all dynamic and static re-
strictions are checked. If some restriction would be
violated by establishing the correspondence, then the
according user action is prohibited by our tool and the
user is informed about the reason for the denial.
Our integration algorithm can be extended by us-
ing heuristics for finding correspondences between the
highlighted ontology elements. This could be linguis-
tic similarity measures like in (McGuiness et al., 2000)
or heuristics, which take the structure of the ontology
graph into account, like in (Noy and Musen, 2001). In
this way, it could be possible, to achieve a high degree
of automation of the integration process. Correspon-
dences between highlighted ontology elements would
be automatically generated, if their similarity measure
would succeed a certain threshold, and their definition
would not violate any restrictions. User interaction
would only be required in undecidable cases. We did
not follow this approach, because our main focus lied
on the support for interactive ontology integration.
6 TOOL SUPPORT
We implemented our approach by developing a graph-
based tool for ontology integration. We used the
graph rewriting system PROGRES (Sch
¨
urr et al., 1997)
to specify transformations on a so-called host graph,
which contains the representations of the source on-
tologies, the correspondences and the resulting merged
ontology. The application logic, which constitutes
the core part of the integration tool, was generated
from this specification. The graphical user interface
of the integration tool was realized by means of the
UPGRADE framework (B
¨
ohlen et al., 2002).
Our visual graph-based tool provides an abstrac-
tion of the internal data structure and provides a user-
friendly and problem-adequate representation. We
evaluated the applicability of our approach and the effi-
ciency of our integration tool, by merging several large
ontologies from the domain of building design. The
merged ontologies contained the relevant concepts for
the definition of knowledge for the conceptual design
of the university hospital in Aachen.
7 CONCLUSIONS
In this paper we presented a novel approach for interac-
tive ontology integration. Several different ontologies
can be merged into one. The ontologies are integrated
one by one, while the structure of the resulting merged
ICEIS 2008 - International Conference on Enterprise Information Systems
18
Equivalence correspondence between 1 and 2 not allowed in the following case:
1 X 2 1
X
2
1
X
2
Generalization correspondence from S to G not allowed in the following case:
G X S G
X
S
G X
S
Overlap correspondence between 1 and 2 not allowed in the following case:
1 X2
a)
b)
c)
Ontology elements Possible relations of extensions
o1 2X
G SX
1 SX
o
Figure 4: Examples for dynamic restrictions for correspondences.
ontology is independent of the order, in which they are
integrated. The alignment of the ontologies relies on
the definition of semantic correspondences between
their elements. These correspondences are manually
defined by a knowledge engineer. The knowledge en-
gineer is supported by our graph-based tool in many
ways. Alignment and merging steps alternate through-
out the integration process. The intermediate result
of the integration is immediately updated after each
definition of a correspondence. That way, the effects
of defined correspondences on the integration result
become directly visible. The user is guided through the
merged ontology, and his attention is focused on small
parts of the ontology, where he has to define new cor-
respondences. In this way, the common problems of
finding corresponding ontology elements and defining
the correspondences in the right order are substantially
reduced. The integrity of all defined correspondences
is ensured, because actions, which would violate it, are
prohibited by the tool. Thereby, all restrictions, which
arise through previously defined correspondences, are
taken into account. We identified static and dynamic
restrictions, which may prohibit the definition of cer-
tain correspondences, and motivated these restrictions
by looking at the extensions of corresponding con-
cepts. The integration algorithm can be extended by
using heuristics for generating suggestions for corre-
spondences. Thereby, a high degree of automation of
the integration process could be achieved. The com-
bination of the two approaches – the calculation of
suggestions for correspondences using heuristics on
the one hand, and the restriction of possible correspon-
dences on the other hand – would probably enable the
tool, to make reliable estimations about the correct
correspondences between ontology elements. So far,
our focus lied on the support for interactive ontology
integration. Nevertheless, it would be a promising ap-
proach, to combine our concepts with approaches for
automatic ontology integration.
REFERENCES
B
¨
ohlen, B., J
¨
ager, D., Schleicher, A., and Westfechtel, B.
(2002). UPGRADE: Building Interactive Tools for Vi-
sual Languages. In Callaos, N., Zheng, B., and Kader-
ali, F., editors, Proc. of the 6th World Multiconference
on Systemics, Cybernetics, and Informatics (SCI 2002),
pages 17–22, New York. TPA Publishing.
Euzenat, J. (2004). State of the Art on Ontology Alignment.
Technical Report D2.2.3, Knowledge Web Consortium.
G
´
omez-P
´
erez, A., Fern
´
andez-L
´
opez, M., and Corcho, O.
(2004). Ontological Engineering: With Examples from
the Areas of Knowledge Management, e-Commerce
and the Semantic Web. Springer.
G
´
omez-P
´
erez, A., Gruninger, M., Stuckenschmidt, H., and
Uschold, M., editors (2001). Proc. of the IJCAI–01
Workshop on Ontologies and Information Sharing, Or-
lando, Florida. AAAI Press.
Guarino, N. (1998). Formal Ontology and Information Sys-
tems. In Guarino, N., editor, Proc. of the 1st Intl. Conf.
on Formal Ontology in Information Systems (FOIS’98),
pages 3–15, Amsterdam. IOS Press.
Hakimpour, F. and Geppert, A. (2001). Resolving Semantic
Heterogeneity in Schema Integration: an Ontology
Based Approach. In Proc. of the 2nd Intl. Conf. on
Formal Ontology in Information Systems, volume 2001,
pages 297–308, New York, USA. ACM Press.
Kalfoglou, Y. and Schorlemmer, M. (2003). Ontology Map-
ping: The State of the Art. The Knowledge Engineering
Review, 18(1):1–31.
Klein, M. (2001). Combining and Relating Ontologies: An
Analysis of Problems and Solutions. In (G
´
omez-P
´
erez
et al., 2001), pages 53–62.
Kraft, B. (2007). Semantische Unterst
¨
utzung des
konzeptuellen Geb
¨
audeentwurfs. Dissertation, RWTH
Aachen University, Aachen.
INCREMENTAL ONTOLOGY INTEGRATION
19

McGuiness, D. L., Fikes, R., Rice, J., and Wilder, S. (2000).
An Environment for Merging and Testing Large On-
tologies. In Giunchiglia, F. and Selman, B., editors,
Proc. of the 17th Intl. Conf. on Principles of Knowl-
edge Representation and Reasoning (KR-2000), pages
483–493, San Francisco, USA. Morgan Kaufmann Pub-
lishers.
Noy, N. F. and Musen, M. A. (2000). PROMPT: Algorithm
and Tool for Automated Ontology Merging and Align-
ment. In Engelmore, R. and Hirsh, H., editors, Proc.
of the 12th Conf. on Innovative Applications of Artifi-
cial Intelligence (IAAI-2000), pages 450–455, Orlando,
Florida. AAAI Press.
Noy, N. F. and Musen, M. A. (2001). Anchor-PROMPT:
Using Non-Local Context for Semantic Matching. In
(G
´
omez-P
´
erez et al., 2001), pages 63–70.
Pinto, H. S., G
´
omez-P
´
erez, A., and Martins, J. P. (1999).
Some Issues on Ontology Integration. In Benjamins,
V. R., Chandrasekaran, B., G
´
omez-P
´
erez, A., Guarino,
N., and Uschold, M., editors, Proc. of the IJCAI–99
Workshop on Ontologies and Problem-Solving Meth-
ods: Lessons Learned and Future Trends (KRR5), vol-
ume 18 of CEUR Workshop Proceedings, pages 7/1–
7/12, Aachen. Departement of Computer Science 5,
RWTH Aachen.
Sch
¨
urr, A., Winter, A., and Z
¨
undorf, A. (1997). The PRO-
GRES approach: Language and environment. In Ehrig,
H., Engels, G., Kreowski, H.-J., and Rozenberg, G., ed-
itors, Handbook on Graph Grammars and Computing
by Graph Transformation: Applications, Languages,
and Tools, volume 2, pages 487–550. World Scientific.
Wache, H., V
¨
ogele, T., Visser, U., Stuckenschmidt, H.,
Schuster, G., Neumann, H., and H
¨
ubner, S. (2001).
Ontology-Based Integration of Information – A Survey
of Existing Approaches. In (G
´
omez-P
´
erez et al., 2001),
pages 108–117.
ICEIS 2008 - International Conference on Enterprise Information Systems
20
