A NOVEL APPROACH TO MODEL AND EVALUATE

DYNAMIC AGILITY IN SUPPLY CHAINS

Vipul Jain and Lyès Benyoucef

INRIA COSTEAM Project, ISGMP Bat. A, Ile du Saulcy, 57000 Metz, France

Keywords: Agility, fuzzy logic, multi-agents, supply chain management.

Abstract: In this paper, we propose a novel approach to model agility and introduce Dynamic Agility Index (DA

)

through fuzzy intelligent agents. Generally, it is difficult to emulate human decision making if the

recommendations of the agents are provided as crisp, numerical values. The multiple intelligent agents used

in this study communicate their recommendation as fuzzy numbers to accommodate ambiguity in the

opinion and the data used for modeling agility attributes for integrated supply chains. Moreover, when

agents operate based on different criteria pertaining to agility like flexibility, profitability, quality,

innovativeness, pro-activity, speed of response, cost, robustness etc for integrated supply chains, the ranking

and aggregation of these fuzzy opinions to arrive at a consensus is complex. The proposed fuzzy intelligent

agents approach provides a unique and unprecedented attempt to determine consensus in these fuzzy

opinions and effectively model dynamic agility. The efficacy of the proposed approach is demonstrated with

the help of an illustrative example.

1 INTRODUCTION

An agile supply chain is seen as a dominant

competitive advantage in today’s business; however,

the ability to build an agile supply chain has

developed more slowly than anticipated (Lin et al.,

2006). The need for agility for competitiveness has

traditionally been associated with the supply chains

that provide and manufacture innovative products,

such as high-technology industry products

characterized by shortened life-cycles, a high degree

of market volatility, uncertainty in demand, and

unreliability in supply. Similarly, traditional, more

slow moving industries face such challenges in

terms of requirements for speed, flexibility,

increased product diversity and customization.

Consequently, the need for agility is becoming more

prevalent. These demands come, typically, from

further down the supply chain in the finishing sector,

or from end customers (Gunasekaran and Ngai,

2004).

According to Kidd (1994), Supply Chain

Management (SCM) is a fairly well defined topic,

but agility is not so well defined. Agility can be

something that companies achieve without realizing

it, or it can relate to issues that are difficult to

quantify. The nature of the competencies implied by

agility is such that they would be better considered

as intangibles, similar to intellectual property,

company specific knowledge, skills, expertise, etc.

In summary, SCM and agility combined are

significant sources of competitiveness in the

business world. Thus, it is no surprise that they are

favored research areas in the academic research

world (Swafford et al., 2006).

The fact that agile attributes are necessary but

not sufficient conditions for agility points to a major

research issue to be addressed (Yusuf et al. 2004). It

is essential that the attributes are transformed into

strategic competitive bases of speed, flexibility,

proactivity, innovation, cost, quality, profitability

and robustness. More importantly, these attributes

are of very little significance to practitioners unless

there is a way of deploying them. In addition, the

changing nature of the market requirements suggests

the need for a dynamic deployment tool for

evaluating agility.

There is a growing body of literature on different

aspects of agility (Jain et al. 2008). Collectively,

these contributors and many others (Kumar and

Motwani, 1995), provide insights to what constitute

attributes of an agile supply chain. However, there is

no methodology and tools for introducing and

implementing such a complex and dynamic

Jain V. and Benyoucef L. (2008).

A NOVEL APPROACH TO MODEL AND EVALUATE DYNAMIC AGILITY IN SUPPLY CHAINS.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - SAIC, pages 93-100

DOI: 10.5220/0001684500930100

 SciTePress

interactive system as agile supply chains (Lin et al.,

2006).

Whilst the needs of integrated supply chain

networks have been to a large extent identified, there

is a lack of suitable and commercially available tools

to satisfy these. Therefore, a new generation tools

should be developed and the existing tools

significantly enhanced to support decision-making

processes and to deliver required solutions to

extended businesses. Most agility measurements are

described subjectively by linguistic terms, which are

characterized by ambiguity and multi-possibility.

Thus, the scoring of the existing techniques can

always be criticized, because the scale used to score

the agility capabilities has two limitations:

 Such techniques do not take into account the

ambiguity and multi-possibility associated

with the mapping of one’s judgment to a

number, and

 The subjective judgment and the selection and

preference of evaluators have a significant

influence on those methods.

1.1 Extracted Motivations

Based on the above discussions, we have extracted

the following motivations for this study:

Motivation 1: All companies, suppliers,

manufacturers, distributors, and even customers,

may have to be involved in the process of achieving

an agile supply chain (Christopher and Towill,

2001).

Motivation 2: The lack of a systematic approach

to agility does not allow companies to develop the

necessary proficiency in change, a prerequisite for

agility ( Lin et al., 2006).

Motivation 4: Most agility measurements are

described subjectively by linguistic terms, which are

characterized by ambiguity and multi-possibility.

Thus, the scoring of the existing techniques can

always be criticized, because the scale used to score

the agility capabilities has limitations (Lin et al.,

2006).

Motivation 5: The fact that agile attributes are

necessary but not sufficient conditions for agility

points to a major research issue to be addressed

(Yusuf et al. 2004). It is essential that the attributes

are transformed into strategic competitive bases of

speed, flexibility, proactivity, innovation, cost,

quality, profitability and robustness.

Motivation 6: There is no methodology and

tools for introducing and implementing such a

complex and dynamic interactive system which

incorporate both quantitative and qualitative

attributes as agile supply chains (Lin et al., 2006).

1.2 Outlines and our Contributions

In embracing integrated agile supply chain many

important questions concerning agility need to be

asked (Jharkaria and Shankar 2005) such as:

 What precisely is agility and how it can be

measured?

 How to develop an integrated agile supply

chain?

 How will agile supply chains know what they

have it, as there are no simple metrics or

indexes available?

 How and to what degree does the integrated

agile supply chain attributes affect supply

chains business performance?

 How to compare agility with competitiveness?

 How can the integrated supply chains identify

the principal obstacles to improvement, if a

supply chain wants to improve agility?

 How to assist in achieving agility effectively?

Answers to such questions are critical to the

practitioners and to the theory of integrated agile

supply chains design. However, it is difficult to

emulate human decision making if the

recommendations of the agents are provided as

crisp, numerical values. Intelligent agents must

express their opinions in similar terms to emulate

human experts. Moreover at times, the agents make

their recommendations based upon incomplete or

unreliable data. A second problem arises when

intelligent agents base their opinions on different

viewpoints.

Therefore, we introduce a novel concept of

Dynamic Agility Index (DA

) to model agility in

integrated supply chains. More specifically, this

paper describes an effort in developing an approach

to determine a consensus without requiring that the

agent opinions have any agreement for modeling

agility attributes in integrated supply chains. The

multiple intelligent agents used in the paper

communicate their recommendation as fuzzy

numbers to accommodate ambiguity in the opinion

and the data used for supply chains.

2 AGILITY AND SUPPLY CHAIN

Parallel developments in the areas of agility and

SCM led to the introduction of an agile supply chain

(Christopher 2000). While agility is accepted widely

as a winning strategy for growth, even a basis for

ICEIS 2008 - International Conference on Enterprise Information Systems

survival in certain business environments, the idea

of creating agile supply chains has become a logical

step for companies. Agility in a supply chain,

according to Ismail and Sharifi (2005), is the ability

of the supply chain as a whole and its members to

rapidly align the network and its operations to

dynamic and turbulent requirements of the

customers. The main focus is on running businesses

in network structures with an adequate level of

agility to respond to changes as well as proactively

anticipate changes and seek new emerging

opportunities.

Agile supply chain concerns change, uncertainty

and unpredictability within its business environment

and makes appropriate responses to changes.

Therefore, an agile supply chain requires various

distinguishing capabilities, or “fitness”. These

capabilities include four main elements:

 Responsiveness, which is the ability to identify

changes and respond to them quickly,

reactively or proactively, and also to recover

from them;

 Competency, which is the ability to efficiently

and effectively realize enterprise objectives;

 Flexibility/adaptability, which is the ability to

implement different processes and apply

different facilities to achieve the same goals;

 Quickness/speed, which is the ability to

complete an activity as quickly as possible.

Van Hoek (2005) observes that three

characteristics of supply chain operations can be

earmarked as directly related to becoming agile: 1)

mastering and benefiting from variance, 2) rapid

responsiveness, and 3) unique or small volume

responsiveness. In addition, many researchers

provide conceptual overviews, different reference

and mature models of agility (Christopher 2000,

Yusuf et al. 2004, Ismail and Sharifi (2005)).

There has been quite a clear vision of the

benefits of creating an agile supply chain. However,

there is a shortage of studies and cases of companies

actually turning the vision or ambition into reality,

let alone tools that they use to do so. It is essential

that the attributes are transformed into strategic

competitive bases of speed, flexibility, proactivity,

innovation, cost, quality, profitability and

robustness. More importantly, these attributes are of

very little significance to practitioners unless there is

a way of deploying them. In addition, the changing

nature of the market requirements suggests the need

for a dynamic deployment tool. This forms the

motivation for our problem environment, which is

described in the next section of the paper.

3 PROBLEM ENVIRONMENT

The agility in supply chains is determined by certain

time variables, which we refer to here as ‘agility

characteristics’. The rate of change of these

characteristics is a function of the current values of

all the attributes as well as some suitable ‘input’

variables, like the size and numbers of teams,

refereed as team formation, the level of integration

of the database. The proposed dynamic agility index

(DA

) of an integrated supply chain can be given a

numerical value calculated as the sum of the

products of suitable ‘economical bases’, i.e.

1234

567 8

Li X T L V

RTB

AWFWPWQWI

WPWS WCWR

×+×+×+×

×+×+× +×

Where:

1. F

is a measure of Flexibility, and W

is a

weight assumed constant but time varying in

general,

2. P

is a measure of Profitability, and W

is a

weight assumed constant but time varying in

general,

3. Q

is a measure of Quality, and W

is a weight

assumed constant but time varying in general,

4. I

is a measure of Innovation, and W

is a

weight assumed constant but time varying in

general,

5. P

is a measure of Profitability, and W

is a

weight assumed constant but time varying in

general,

6. S

is a measure of Speed of response, and W

a weight assumed constant but time varying in

general,

7. C

is a measure of Cost, and W

is a weight

assumed constant but time varying in general,

8. R

is a measure of Robustness, and W

is a

weight assumed constant but time varying in

general,

Let us assume that these variables form the

output vector (

) of the dynamical agility model,

i.e.

(1,2,3,4,5,6,7,8)

(,, ,,,, ,)

XT LVRR TB

OT OT OT OT OT OT OT OT OT

FPQIPSCR

The mathematical model developed is based on

dynamical systems theory and recognizes that the

integrated supply chains attributes have evolutionary

approaches.

A NOVEL APPROACH TO MODEL AND EVALUATE DYNAMIC AGILITY IN SUPPLY CHAINS

4 THE PROPOSED APPROACH

WITH AN ILLUSTRATIVE

EXAMPLE

In this section, we present an illustrative example for

the proposed Fuzzy Intelligent agent framework to

study and model the agility for integrated supply

chains. The stepwise procedure is shown as follows:

Step 1: Select criteria for evaluation. Based on

the literature, we have listed several important

criteria for modeling agility for evaluation of

integrated supply chains. These include the

following: Flexibility (F

), Profitability (P

), Quality

), Innovation (I

), Pro-activity (P

), Speed of

response (S

), Cost (C

), Robustness (R

An agile supply chain must be able to withstand

the aforementioned variations and disturbances and

indeed must be in a position to take advantage of

these fluctuations to maximize their profits. These

selected eight criteria’s and their possible

combinations abbreviated as (C

, C

) are listed in Table 1. The agility of

integrated supply chains can be given a numerical

value calculated as the sum of the products of the

aforementioned criteria and their possible

combinations as given in Table 1. The eight

criteria’s listed above are by no means exhaustive

and therefore new factors may be added depending

on the product, industry and market characteristics.

Step 2: Determine the appropriate linguistic

scale to assess the performance ratings and

importance weights of the agility capabilities. An

agile supply chain means that the production process

must be able to respond quickly to changes in

information from the market. This requires lead time

compression in terms of the flow of information and

material and the ability to change at short notice, to

change to a wide variety of products. In many cases,

it is virtually impractical for agents to directly

determine the score of a vague indicator, such as

measure of quality or the speed of response or

innovation. Therefore, in this research, linguistic

terms are used to assess the performance rating and

importance weights of the agility capabilities for

integrated supply chains.

Noteworthy, many popular linguistic terms and

corresponding membership functions have been

proposed for linguistic assessment. In addition, the

linguistic variables selected to assess the importance

weights of the agility capabilities are {Very High

(VH), High (HG), Fairly High (FH), Medium (M),

Fairly Low (FL), Low (L), Very Low (VL)}.

Step 3: Measure the importance and the

performance of agility capabilities using linguistic

terms. Once the linguistic variables for evaluating

the performance ratings and the importance weights

of the agility capabilities are defined, according to

the supply chains policy and strategy, profile,

characteristics, business changes and practices,

marketing competition information, the agents can

directly use the linguistic terms above to assess the

rating which characterizes the degree of the

performance of various agility capabilities.

The results, integrated performance ratings and

integrated importance weights of agility capabilities

measured by linguistics variables, are shown in

Table 2.

Step 4: Approximate the linguistic terms by

fuzzy numbers. We perform trapezoidal

approximations of fuzzy numbers. Tapping the

properties of trapezoidal fuzzy numbers, a set of

fuzzy numbers for approximating linguistic variable

values was developed as shown in Table 3.

Step 5: Cumulate fuzzy opinions with fuzzy

weights. Several aggregation techniques require that

the fuzzy opinions have some intersection so that

they are not entirely out of agreement. In case, the

opinions do not have some agreement, the agents

negotiate until they can arrive at a consensus.

However, these methods will not be considered, as

agents assumed in this research may intentionally

have disparate recommendations due to their diverge

viewpoints for supply chain management.

Weighted linear interpolation is used to

aggregate the opinions for every alternative, incase,

there is no common interaction between agent

opinions. Each agent,

, is assigned a rating,

The most crucial agent is specified a rating of 1 and

the others are given ratings less than 1, in relation to

their significance. To the ratings the following

properties holds:

Maximum (

…,

) = 1

Minimum (

…,

) < 1

The degree of significance (DOS) is defined as:

DOS 1,2,3,...,

=Π = =

∑

(1)

The cumulated fuzzy opinion for alternative

is formed as a Trapezoidal fuzzy number (TFN)

tuple (



) using formulas:

ICEIS 2008 - International Conference on Enterprise Information Systems

112 2

3344

δδ

ξξ ξ ξ

ξξ

δδ

ξξ ξξ

ξξ

λλ

⎧

=Π =Π

⎪

⎨

⎪

=Π =Π

⎪

⎩

∑∑



(2)

where

is the number of agents with opinions

on alternatives

Π corresponds to the degree of

significance of agent

and (

)

symbolizes TFN opinion of agent

for alternative

. The resulting inferred aggregated opinion

(



) can be represented as:

()

)( RRI

∑

Π=

(3)

where

= (

) and )(D is the

fuzzy multiplication operator.

Thus, the trapezoidal fuzzy membership function

is used to determine the agility level and the required

fuzzy index of the selected criteria can be calculated

as above equation (3).

(7, 8, 9,10) (0.7, 0.8,0.9,1.0) (7,8,9,10) (0.7,0.8,0.9,1.0)

(7,8,9,10) (0.7, 0.8,0.9,1.0) (7,8,9,10) (0.35,0.45,0.55,0.65)

(7, 8, 9,10) (0.5,0.6,0.7, 0.8) (7,8,9,10) (0.7, 0.8,0.9,1.0)

(7,8,9,10) (0.35,0.

⊗⊕⊗

⊕⊗ ⊕⊗

⊕⊗ ⊕ ⊗

⊕⊗

45,0.55,0.65) (7,8,9,10) (0.5,0.6,0.7, 0.8)

(0.7, 0.8,0.9,1.0) (0.7, 0.8,0.9,1.0) (0.7, 0.8,0.9,1.0)

(0.35,0.45,0.55,0.65) (0.5,0.6,0.7,0.8) (0.7,0.8,0.9,1.0)

(0.35,0.45,0.55,0.65) (0.5,0.6,0.7

⎡⎤

⎢⎥

⊕⊗

⎣⎦

⊕⊕

⊕⊕⊕

⊕⊕

(7,8,9,10)

,0.8)

⎡⎤

⎢⎥

⎣⎦

Applying the same equation the other fuzzy

indexes of agility criteria are obtained. Finally,

applying the same equation again, we calculate the

proposed Dynamic Agility level index (DA

) for

modeling agility for integrated supply chains with

the taken 8 criteria and their all possible

combinations is evaluated as:

(7,8,9,10) (0.7,0.8,0.9,1.0)

(5,6.04,7,8) (0.5,0.6,0.7,0.8)

(3.49,4.51,5.5,6.52) (0.7,0.8,0.9,1.0)

(2.52,3.5,4.5,5.56) (0.5,0.6,0.7, 0.8)

(3.5,4.5,5.5,6.5) (0.35,0.45,0.55,0.65)

(5,6,7,8) (0.5,0.6

⊗

⊕⊗

,0.7,0.8)

(3.52,4.5,5.48, 6.25) (0.7,0.8,0.9,1.0)

(5,6, 7,8) (0.35,0.45,0.55,0.65)

(0.7,0.8,0.9,1.0) (0.5,0.6,0.7, 0.8)

(0.7,0.8,0.9,1.0) (0.5,0.6,0.7,0.8)

(0.35,0.45,0.55,0.65) (0

⎡⎤

⎢⎥

⊕⊗

⎢⎥

⊕⊗

⎣⎦

⊕

⊕⊕

(4.544,5.486, 6.352,6.982)

.5,0.6,0.7,0.8)

(0.7,0.8,0.9,1.0) (0.35,0.45,0.55,0.65)

⎡⎤

⎢⎥

⊕⊕

⎣⎦

Step 6: Rank the fuzzy opinions. The superior

alternative must be chosen, once the opinions of the

agents have been aggregated to produce a consensus

opinion for each alternative. The findings of

Nakamura (1986) emphasize a fuzzy preference

function that outline a comparison index, which

compares opinions

k and

k that accounts for the

hamming distance of every fuzzy number to the

fuzzy minimum and the fuzzified best and worst

states. The FFCF is defined as:

(

)

()

** *

(, )

ii j

pi j

KK K

βχ

⎧

⎡⎤

∧

⎪

⎢⎥

≠

⎪

⎢⎥

+− ∧

⎣⎦

⎨

⎪

⎩

(4)

where :

(

)

(

)

()()

** * ** *

(1 ) , ,

ii j ji j

KK K K K K

ϖβχ χ

βχ χ

⎡

⎤

∧+ ∧ +

⎣

⎦

⎡

⎤

−∧+∧

⎣

⎦

{}

VSup

∈∀

≥

φθθ

)()(

(5)

Further,

K is the highest upper set of

defined by:

{}

() ()

Sup V

θθ φ

φμθφ

≤

∀∈

(6)

∧

is the extended minimum defined by

{}

() [ () ()]

ij i j

KK K K

Sup V

θφθ φ σ

σμθμφσ

∧

∧=

∧∀=

(7)

and the Hamming distance between

K and

K is

given by

),(

, which is

(, ) () ()

ij K K

KK d

μθ μθ θ

=−

∫

(8)

Theoretically,

(

)

***

jii

KKK ∧

and

(

)

***

jii

KKK ∧

signifies the advantages of

over

K with respect to the fuzzified worst states

and the fuzzified best states. The fraction of the

weighted combination of the advantages of

K and

K over the worst states and the above the best

states, to the sum of such weighted combinations of

K ’s and

K ’s is represented by the fuzzy first

choice function (FFCF),

),(

jip

In this paper, the fuzzy first choice function

compares every fuzzy opinion to a “Standard” fuzzy

number, which demonstrates the case where the

opinion is “Most Likely”. Hence, the difficulty with

existing methods suffers when comparing fuzzy

numbers with identical modes and symmetric

spreads is eliminated. Also, in this paper, the fuzzy

A NOVEL APPROACH TO MODEL AND EVALUATE DYNAMIC AGILITY IN SUPPLY CHAINS

opinions are not only judge against “Most Likely”

fuzzy numbers but also are already ranked in

contrast to this value, thus eliminating the procedure

of determining the ranking based on pairwise

comparison. The result of every fuzzy first choice

calculation for every node presents its ranking. The

FFCF evaluating opinion

K and the most likely

mode, M, substitutes the second fuzzy opinion with

M and is defined as:

(

)

()

** *

(, )

ii j

KK K

KK M

βχ

⎧

⎡⎤

∧

⎪

⎢⎥

≠

⎪

⎢⎥

+− ∧

⎣⎦

⎨

⎪

⎩

(9)

The FFCF can be simplified by showing that

(

)

** *

, 0

KK M

∧ = , when M is a TFN defined as

(, ,1,1)

. Thus, if M is signified by

(, ,1,1)

, the modified fuzzy first choice

function used to evaluate opinion

with the most

likely mode, M, is defined as:

()

(, )

KK M if

βχ ϖ

⎧

∧≠

⎪

⎨

⎪

⎩

(10)

where :

** *

(, ) (, )

(1 ) ( , )

ii i

KK M MK M

MK M

ϖβχ χ

βχ

⎡⎤

=∧+∧

⎣⎦

+− ∧

This fuzzy first choice function is able to

distinguish between fuzzy numbers with identical

modes and symmetric spreads while reducing the

computational complexity. Ranks for dynamic

agility index for selected agility criteria are given in

Table 4.

Step 7: Match the fuzzy opinions with an

appropriate agility level. In this case the natural

language expression set selected is given as:

Exceedingly Agile (EA), Very Agile (VA),

Agile (AG), Fairly Agile (FA), Most Likely Agile

(MLA), Slowly Agile (SA), No Agile (NA).

The linguistics and the corresponding

membership functions are shown in Figure 6. The

Euclidean distance ED is calculated by using the

Euclidean distance formula as given in Equation

(11) below:

()

(,) () ()

LN AG F

ED AG F f x f x

∈

⎛⎞

=−

⎜⎟

⎝⎠

∑

(11)

Where

{

}

[

]

, ,..., 0, 10

Pxx x=⊂ so that

0...10

xx x

<<< =.

The ED for the selected set of natural expression

set is given as: ED (EA)= 1.2364, ED(VA)= 0.0424,

ED(AG)= 1.0241, ED(FA)= 1.1462, ED(MLA)=

1.5321, ED(SA)= 1.6422 and ED(NA)= 1.8041.

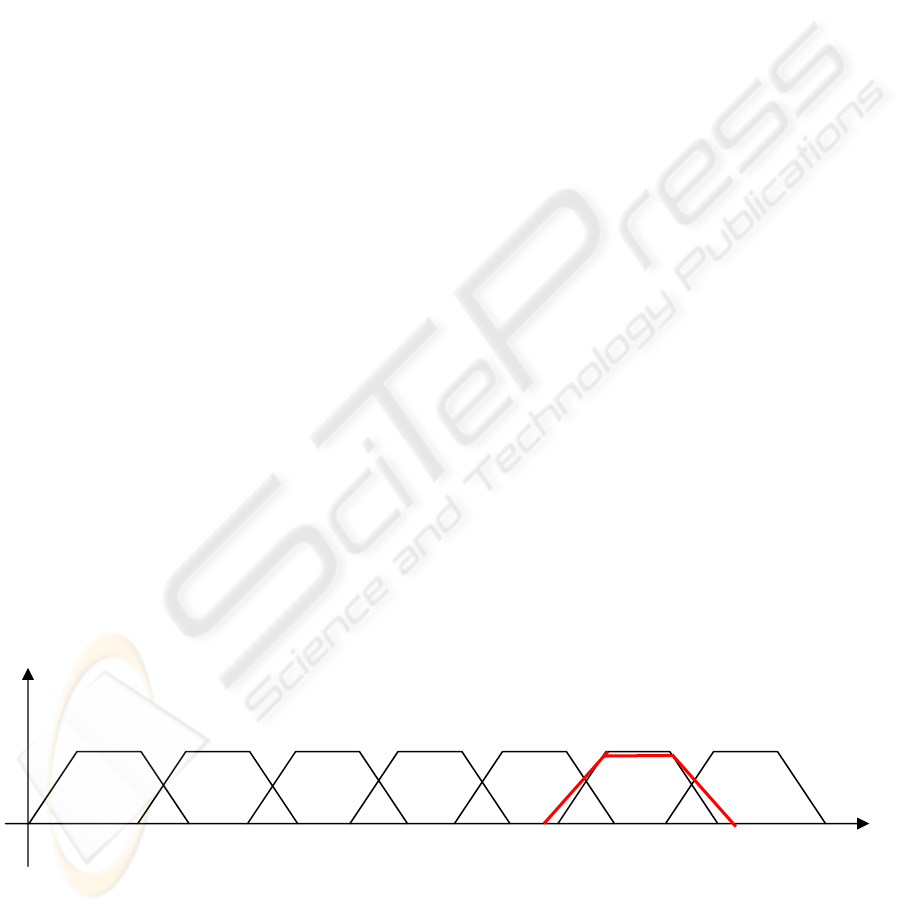
Thus, by matching a linguistic label with the

minimum ED, dynamic agility can be modeled with

the given criteria’s. From the Figure 6, it can be

seen that the selected eight criteria (F

, P

, Q

, I

, S

, C

, R

), the supply chain falls under the Very

Agile (VA) category. Depending on the selected

criteria, for any supply chains, the proposed

approach will help the decision makers and analysts

in quantifying agility.

Step 8: Analyze and classify the main obstacles

to improvement. Modeling agility not only measures

how agile is integrated supply chain, but also most

importantly helps supply chain decision makers and

practitioners to assess distinctive competencies and

identify the principal obstacles for implementing

appropriate improvement measures. In supply chain

network, the factual environment of the problem

engrosses statistics, which is repeatedly fuzzy and

indefinite. As customer’s demands are always

uncertain, manufacturers tend to manage their

suppliers in different ways leading to a supplier-

supplier development, supplier evaluation, supplier

association, supplier coordination etc.

5 CONCLUSIONS AND

PERSPECTIVES

In this paper, we propose a novel approach to model

agility and introduce Dynamic Agility Index (DA

)

through fuzzy intelligent agents The proposed

approach concentrates on the application of

linguistic approximating, fuzzy arithmetic and agent

technology is developed to address the issue of

agility measuring, stressing the multi-possibility and

ambiguity of agility capability measurement.

When agents operate based on different criteria

pertaining to agility like flexibility, profitability,

quality, innovativeness, pro-activity, speed of

response, cost, robustness, etc., for integrated supply

chains, the ranking and aggregation of these fuzzy

opinions to arrive at a consensus is complex.

ICEIS 2008 - International Conference on Enterprise Information Systems

Although, the dynamic agility index is conveyed

in a range of values, the proposed approach ensures

that the decision made in the selection using the

fuzzy intelligent agents will not be biased. For the

numerical example considered in this study, the

dynamic agility index has a fuzzy value of

(4.544,5.486,6.352,6.982), which falls under Very

Agile (VA) category. Thus, it gives the decision

makers a high degree of flexibility in decision-

making.

As a scope for future work, empirical research is

required to study the application of the model

developed in this paper and to characterize agility in

integrated supply chains. Moreover, we are

involving in European project I*Proms, with several

industrial partners, we expect to apply the proposed

approach to model agility in real life scenarios.

ACKNOWLEDGEMENTS

These researches are supported by the European

Community research program, through the NoE

I*Proms (http://www.iproms.org/). These supports

are gratefully acknowledged.

REFERENCES

Christopher, M. and Towill D., 2001, An integrated model

for the design of agile supply chains. International

Journal of Physical Distribution & Logistics, 31 (4),

234-246.

Christopher, M., 2000, The Agile Supply Chain:

Competing in Volatile Markets. Ind. Marketing

Management, 29(1), 37-44.

Gunasekaran, A. and Ngai E.W.T., 2004, Information

systems in supply chain integration and management.

European Journal of Operational Research, 159, 269–

295.

Ismail, H.S. and Sharifi H., 2005, Supply Chain Design

for supply Chain: A balanced approach to building

agile supply chain. Proceedings of the International

Conference on Agility – ICAM 2005, Finland, 187–

193.

Jain, V., Benyoucef, L. and Deshmukh, S. G., 2008, A

new approach for evaluating agility in supply chains

using fuzzy association rules mining. Engineering

Applications of Artificial Intelligence (international

journal), 21(4).

Jharkharia, S. and Shankar R., 2005, IT-enablement of

supply chains: understanding the barriers. Journal of

Enterprise Information Management, 18(1/2), 11–27.

Kidd, P.T., 1994, Agile Manufacturing. Forging New

Frontiers (Addison-Wesley, London).

Kumar, A. and Motwani J., 1995, A Methodology for

Assessing Time-based Competitive Advantage of

Manufacturing Firms, International Journal of

Operations and Production Management, 15(2), 36-

53.

Lin, C-T., Chiu, H. and Chu, P-Y., 2006, Agility index in

the supply chain. International Journal of Production

Economics,100, 285–299.

Nakamura, K., 1986, Preference relations on a set of fuzzy

utilities as a basis for decision making. Fuzzy Sets and

Systems, 1986, 20(2), 147-162.

Swafford, P. M., Ghosh, S. and Murthy, N. N., 2006, A

framework for assessing value chain agility.

International Journal of Operations and Production

Management, 26(2), 118-140.

van Hoek, R., 2001, Epilogue: Moving forwards with

agility. International Journal of Physical Distribution

and Logistics Management, 31(4), 290-300.

Yusuf,Y. Y., Gunasekaran, A., Adeleye, E. O. and

Sivayoganathan, K., 2004, Agile supply chain

capabilities: Determinants of competitive objectives.

European Journal of Operational Research, 159, 379-

392.

Figure 1: The proposed dynamic agility index (DA

) for the illustrative example.

0 0.5 1 1.5 2 2.5 3 3.5 4

4.5

55.5

6.5

Agility

A SA MLA FA AG VA EA

A NOVEL APPROACH TO MODEL AND EVALUATE DYNAMIC AGILITY IN SUPPLY CHAINS

Table 1: Criteria’s for modeling dynamic agility.

Combination C

criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Combination

of criteria

Flexibility (F

)

Profitability (P

)

Quality (Q

)

Innovation (I

)

Pro-activity (P

)

Speed & response (S

)

Cost (C

)

Robustness (R

)

Table 2: Aggregated performance rating with aggregated important weight for selected agility criteria.

Criteria Weight Rank

0-8

VH VH VH FH H VH FH H VH EP

H H VH H FH H VH VG

VH VH H VH VH VH GD

H FH FH VH FH FR

FH VH H FH GD

H M VH FH

VH FH VG

FH GD

Table 3: Fuzzy numbers for approximating linguistic variables for selected agility criteria.

Performance rating Importance weighting

Linguistic variable Fuzzy number Linguistic variable Fuzzy number

Worst (WT)

Very Poor (VP)

Poor (PR)

Fair (FR)

Good (GD)

Very Good (VG)

Exceptional (EP)

(0, 0.05, 0.25, 1.25)

(1, 2, 3, 4)

(1.5, 2.5, 3.5, 4.5)

(2.5, 3.5, 4.5, 5.5)

(3.5, 4.5, 5.5, 6.5)

(5, 6, 7, 8)

(7, 8, 9, 10)

Very Low (VL)

Low (LW)

Fairly Low (FL)

Medium (MD)

Fairly High (FH)

High (HG)

Very High (VH)

(0, 0.005, 0.025, 0.125)

(0.1, 0.2, 0.3, 0.4)

(0.15, 0.25, 0.35, 0.45)

(0.25, 0.35, 0.45, 0.55)

(0.35, 0.45, 0.55, 0.65)

(0.5, 0.6, 0.7, 0.8)

(0.7, 0.8, 0.9, 1.0)

Table 4: Ranks for dynamic agility index for selected agility criteria.

Criteria Rank

0-8

(7, 8, 9, 10)

(5, 6.04, 7, 8)

(3.49, 4.51, 5.50, 6.52)

(2.52, 3.50, 4.50, 5.56)

(3.50, 4.50, 5.50, 6.50)

(5, 6, 7, 8)

(3.52, 4.50, 5.48, 6.25)

(5, 6, 7, 8)

ICEIS 2008 - International Conference on Enterprise Information Systems

100