
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS
A Branch & Bound Approach
Antonio Juarez Alencar, Eber Assis Schmitz,
ˆ
Enio Pires de Abreu, Marcelo Carvalho Fernandes
Graduate Program in Informatics, Institute of Mathematics and Electronic Computer Center
Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
Armando Leite Ferreira
The COPPEAD School of Business, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
Keywords:
Branch & Bound, Minimum Marketable Feature, Incremental Funding Method, Project Management and
Business Performance.
Abstract:
This work presents a branch & bound method that allows software managers to determine the optimum order
for the development of a network of dependent software parts that have value to customers. In many different
circumstances the method allows for the development of complex and otherwise expensive software from a
relatively small investment, favoring the use of software development as a means of obtaining competitive
advantage.
1 INTRODUCTION
In today’s highly-competitive globalized market,
software development projects are unlikely to be
funded unless they yield clearly-defined low-risk
value to business (McManus, 2003). Moreover,
in such competitive markets stakeholders frequently
call for shorter investment payback time, product-
development faster time-to-market, and a business ar-
chitecture with improved operational agility (Lam,
2004; Helo et al., 2004; Whittle and Myrick, 2005).
All of this requires new approaches to software
project development (Jorgenson et al., 2003; High-
smith, 2002).
To deal with this situation both academics and
software developers have strongly emphasized the
need for methods, concepts and tools that favor the
early delivery of functional parts of software sys-
tems that are valued by customers (Abacus et al.,
2005; Nord and Tomayko, 2006). In this sense, the
Incremental Funding Method, or IFM, is a finan-
cially responsible approach to requirement prioriti-
zation that increases the value creation of software
projects (Denne and Cleland-Huang, 2004a; Denne
and Cleland-Huang, 2004b).
The IFM groups requirements into self-contained
interdependent software units that create value to
business in one or several of the following areas:
• Competitive Differentiation - the software unit al-
lows the creation of service or product features
that are valued by customers and that are different
from anything else being offered in the market;
• Revenue Generation - although the software unit
does not provide any unique valuable features to
customers, it does provide extra revenue by offer-
ing the same quality as other products in the mar-
ket for a better price;
• Cost Savings - the software unit allows business
to save money by making one or more business
processes cheaper to run;
• Brand Projection - by building the software unit
the business projects itself as being technologi-
cally advanced; and
• Enhanced Customer Loyalty - the software unit
influences customers to buy more, more fre-
quently or both.
Moreover, the total value brought to an organiza-
tion by a software consisting of several interdepen-
dent units, each one with its own cash flow and prece-
dence restrictions, is highly dependent on the imple-
mentation order of these units.
162
Juarez Alencar A., Assis Schmitz E., Pires de Abreu Ê., Carvalho Fernandes M. and Leite Ferreira A. (2008).
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS - A Branch & Bound Approach.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - ISAS, pages 162-169
DOI: 10.5220/0001685801620169
Copyright
c
SciTePress
Therefore, the method includes a set of
polynomial-time sequencing strategies that helps
finding a suitable development schedule that im-
proves the overall value of projects, reduce initial
investments, or enhance other project metrics such as
time needed for a project to break even and payback
time (Denne and Cleland-Huang, 2004b; Denne and
Cleland-Huang, 2005).
However, the strategies proposed by the IFM does
not lead, in all circumstances, to the best possible
schedule, which can only be achieved, in the general
case, in an exponential time. Furthermore, in order
to allow the sequencing algorithm to run in a polyno-
mial time, the IFM requires that the development of
a software unit may depend upon the development of
no more than a single software unit.
This work presents a branch & bound method that
finds the schedule that maximizes the business value
of a software project and that imposes no restrictions
on the dependencies that may exist among software
units, making the method more attractive to be used
in the real world. Although, the branch & bound is an
exponential method, there are many circumstances in
which it can find the best possible solution to an opti-
mization problem in a polynomial time. See (Liberti,
2003; Hillier and Lieberman, 2001) for an introduc-
tion to the branch & bound method.
The remaining of this paper is organized as fol-
lows. Section 2 presents a review of the principal con-
cepts and methods used in the article. Section 3 intro-
duced the branch & bound method with the help of an
example. The method is formalized in Section 4. Sec-
tion 5 discusses the implications of the method for dif-
ferent dimensions project management. Finally, Sec-
tion 6 presents the conclusions of this paper.
2 CONCEPTUAL FRAMEWORK
The self-contained units in which the IFM partitions a
software project are called Minimum Marketable Fea-
tures, or MMF for short, indicating that they contain
strongly-related software features that can be quickly
delivered and that are valued by customers (Steindl,
2005; Denne and Cleland-Huang, 2004b).
Although an MMF is a self-contained unit, it is
often the case that an MMF can only be developed
after other project parts have been completed. These
project parts may be either other MMFs or the archi-
tectural infrastructure, i.e. the set of basic features
that offers no direct value to customers, but that are
required by the MMFs.
The architecture itself can usually be decomposed
into self-contained deliverable elements. These el-
ements, called Architectural Elements or AEs for
short, enables the architecture to be delivered accord-
ing to demand, further reducing the initial investment
needed to run a software project. See (Rashid et al.,
2003) for directions on how software module and
architectural elements may be derived from require-
ments.
2.1 Cash Flow
After the MMFs and AEs have been identified, devel-
opers and business personnel collaborate to analyze
for each MMFs and AEs their estimated cost and ex-
pected revenues over a window of opportunity. See
(Hubbard, 2007) for a discussion on how these esti-
mates may be obtained in real-world projects. These
costs and revenues form a cash flow that can be used
to estimate the total value of the software.
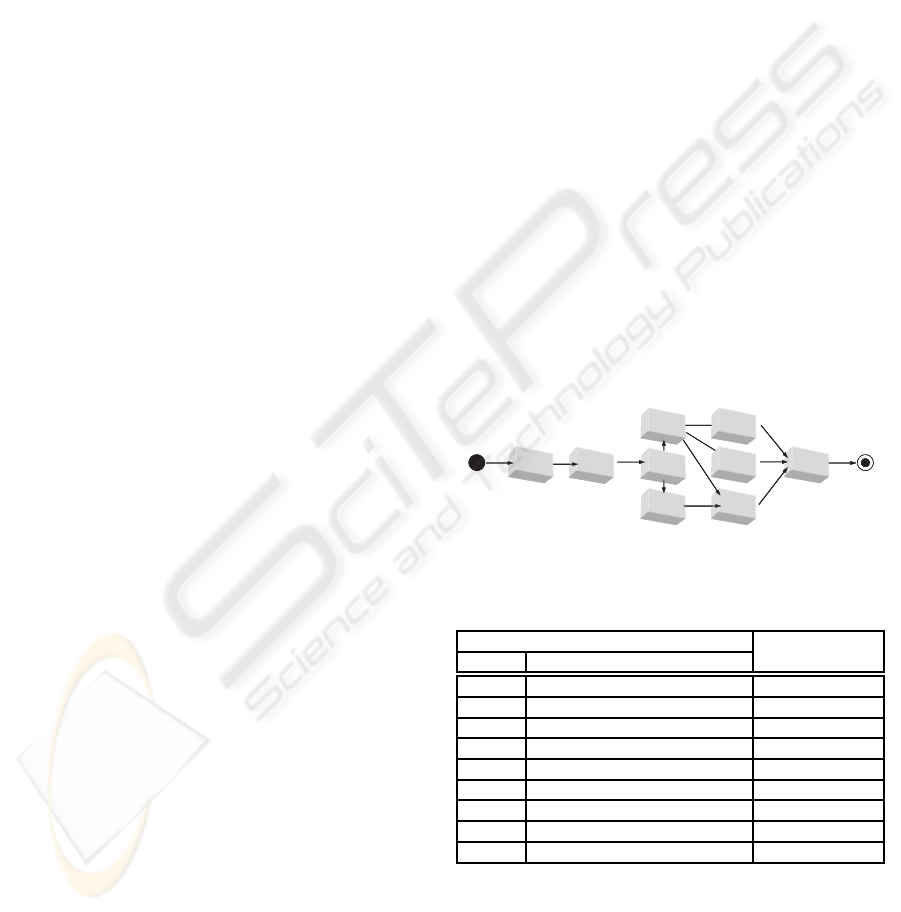
For example, Figure 1 presents a set of interdepen-
dents MMFs and AE’s. In that figure GIL is the first
tool to be developed and CLM the last. Moreover, an
arrow connecting two activities such as PdS → Pc in-
dicates that the latter development efforts may only
start when the former has been completed and all the
necessary resources are available. Table 1 shows the
activity supported by each unit and whether they are
an MMF or an AE.
Start End
PsS
PdS
Pc
CD
LP
CP
CLM
SC
GIL
Start End
PsS
PdS
Pc
CD
LP
CP
CLM
SC
GIL
Figure 1: A precedence graph of project units.
Table 1: List of software units to be developed.
Tool Type of
Name Supported Activity Software Unit
GIL Graphical Interface Library AE
PdS Product Selection MMF
PsS Prospect Selection MMF
Pc Pricing MMF
CD Catalog Design MMF
LP Label Printing MMF
SC Stock Control MMF
CP Catalog Printing MMF
CLM Catalog Labeling & Mailing MMF
Table 2 shows the expected cash flow for the set
of project units presented in Figure 1. In that table
periods are time interval of equal length, where an
investment is made or a revenue is earned.
In formal terms a window of opportunity P is a
set {p
1
, p
2
, ··· , p
k
} of time periods of equal length.
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS - A Branch & Bound Approach
163

In Table 2, P = {1, 2, ··· , 12}. Also, the cash-flow of
a project unit v
i
is given by cf(v
i
) and the cash flow
element of v
i
in period p ∈ P is given by cf(v
i
, p). In
Table 2, cf(CD) at period 1, i.e. cf (CD, 1), is -70 and
cf(CD) in period 2, i.e. cf(CD, 2), is 20.
2.2 The Precedence Relationship
The development constraints between MMFs and
AEs can be represented by a directed acyclic graph
showing their precedence relationship. Figure 1 in-
troduces one of these graphs. In that graph, Start and
Finish are dummy units that take no time to be exe-
cuted and yield no cash flows, signaling respectively
the beginning and end of a project.
In formal terms a precedence graph of project
units is a mathematical structure G(V, E) where:
• V = {v
1
, v
2
, · · · , v
n
} is a set of MMFs and AEs,
and
• E is a set of ordered pairs, such that if (v
a
, v
b
) ∈ E,
then v
b
depends on the completion of v
a
.
In the graph presented in Figure 1, V
G
= {Start, GIL,
PdS, ··· , CLM, End} e E
G
= {(Start, GIL), (GIL,
PdS), (PdS, Pc), ··· , (CP, CLM), (CLM, End)}. A
thorough introduction to graph theory can be found in
(Gross and Yellen, 2005).
2.3 Discounted Cash Flow
Because it is improper to perform mathematical op-
erations on monetary values without taking into ac-
count an interest rate, in order to compare the value of
different MMFs one has to resort to their discounted
cashflow (Fabozzi et al., 2006). In formal terms, the
net present value of a software unit v
i
whose develop-
ment starts at period t ∈ P is given by the sum o its
discounted cash flows, i.e.
Table 2: The cash flow of the project units in thousands of
US dollars.
Project Periods
Unit 1 2 3 ·· · 12
GIL -50 0 0 ·· · 0
PdS -40 20 20 ·· · 20
PsS -50 30 30 · ·· 30
Pc -30 15 15 ·· · 15
CD -70 20 20 ·· · 20
LP -20 5 5 ··· 5
SC -200 40 40 ··· 40
CP -50 15 15 ·· · 15
CLM -50 200 200 ·· · 200
npv(v, t) =
n
∑
j=t
cf(v, j −t +1)
(1+
r
100
)
j
,
where r is the discount rate and n is the last period
of the window of opportunity P. For example, if the
development of MMF CD starts in period 1, then its
NPV is
npv(CD, 1) =
−70
(1+
2
100
)
1
+ ·· · +
20
(1+
2
100
)
12
= $123
Table 3 shows the discounted cash-flows of each
MMF in Figure 1, considering a 2% discount rate, at
different starting points within a window of opportu-
nity P. Note that the table considers only the first nine
periods of the window of opportunity, as these are the
periods in which the software units are going to be
developed.
Table 3: The NPVs of the project units in thousands of US
dollars with a discount rate of 2%.
Project Periods
Unit 1 2 3 4 ·· · 9
GIL -49 -48 -47 -46 ·· · -42
PdS 153 134 116 98 ··· 15
PsS 239 211 184 157 ··· 31
Pc 115 101 87 74 ··· 11
CD 123 105 88 71 · ·· -10
LP 28 24 20 15 ··· -5
SC 188 153 119 86 ·· · -71
CP 95 81 68 55 ··· -6
CLM 1870 1679 1491 1307 ·· · 441
The reader should not be surprised that the dis-
counted cash-flow of AE
1
in period 1 is -$49 thousand
and not -$50 as one could have naively expected. One
should keep in mind that although development ser-
vices are earned at the beginning of a period, they
are paid for upon delivered at the end of that pe-
riod, when, according to the discount rate, money is
worth slightly less than at the beginning of the period
(Fabozzi et al., 2006).
2.4 Net Present Value
Obviously, the value of a project depends upon the or-
der in which the software units are developed. For ex-
ample, if the development order of the software units
in Figure 1 is GIL → PdS → Pc → CD → PsS →
SC → CP → LP → CLM, than they yield a revenue
of
vpl(GIL, 1) + vpl(PdS, 2) + ··· +vpl(CLM, 9) =
−$49− $134+ ·· · + $441 = $853
ICEIS 2008 - International Conference on Enterprise Information Systems
164

However, if the development order is GIL → PdS →
Pc → CD → PsS → LP → SC → CP → CLM, than
they yield a revenue of $818.
Because not all sequences of software units neces-
sarily comply with the established precedence restric-
tions (see Figure 1), it is important to formally define
what a valid sequence of units is. In this sense a valid
sequence VS is an ordered set of software units such
that:
• All software units belong to the sequence and are
listed exactly once,
• Only one software unit can be in the implementa-
tion process at any given time period,
• The process of developing a software unit can
only start after its precedent units are completed,
• The first software unit must start in the first period
and
• Apart from the last, there is no time delay between
the end of the implementation of a software unit
and the start of the next one.
It may be the case that some software units take
more than one period to be developed. Therefore,
there is a function D(s
i
) that returns the number of pe-
riods required to develop each software unit v
i
∈ V. In
financial terms the sum of the discounted cash-flow of
a valid sequence of MMFs and AEs is its Net Present
Value, or NPV for short. In formal language
npv(S) = npv(v
1
, 1) +
|S|
∑
i=2
npv(v
i
, 1 +
i−1
∑
j=1
D(v
j
))
where S = v
1
, v
2
, · · · , v
m
is a valid sequence of soft-
ware units belonging to V, |S| is the number of soft-
ware units in the sequence and i is the period in which
v
i
is developed.
2.5 The Branch & Bound Method
The branch & bound method provides one of the most
successful and widely used strategy for solving large
complex non-linear optimization problems (Liberti,
2003). When the problem to be tackled is too difficult
to be solved directly, the branch & bound approach
divides the problem into smaller and smaller subprob-
lems until these subproblems can be directly solved.
Hence, the basic concept underlying the branch &
bound strategy is to divide and conquer.
The dividing (or branching) is done by repeatedly
partitioning the entire set of feasible solutions into
smaller subsets. The conquering is accomplished by
placing a bound on how good the best solution in a
subset can be. A subset is discarded if its bound in-
dicates that it cannot possibly contain an optimal so-
lution for the problem being tackled. This strategy
leads to an algorithms consisting of two steps that
uses a search tree to find the optimum solution. While
the branch step is responsible for growing the tree,
the bound step is responsible for limiting its growth
(Hillier and Lieberman, 2001).
3 A REAL-WORLD INSPIRED
EXAMPLE
Consider a chain of furniture stores that uses cata-
log marketing to increase its sales. On a regular ba-
sis this company edit a catalog with a variety of se-
lected products that are sent to a large group of po-
tential buyers, who are selected from the company’s
database. The proper undertaking of this task requires
that eight activities are efficiently executed within a
tight time-frame, i.e.
1. Product Selection - that chooses the products that
will be advertised in the catalog;
2. Prospect Selection - that identifies the prospects
to whom the catalogs are going to be mailed;
3. Pricing - that establishes the promotional price of
every product to be advertised in the catalog;
4. Catalog Design - where the graphic and textual
aspect of the catalog, and accompanying advertis-
ing material are conceived and put together;
5. Label Printing - where labels with prospects’
names and addresses are printed and organized;
6. Stock Control - that makes sure that the products
advertised in the catalog will be available for ship-
ping when they are ordered;
7. Catalog Printing - where the actual print of the
catalog is done;
8. Catalog Labeling & Mailing - which labels the
catalogs with prospects’ names and addresses and
sends them to their intended destinations over the
mail.
With the view of increasing the efficiency of its
catalog marketing campaigns, the company has de-
cided to develop a system of software tools that,
working together, provide adequate support for the
activities leading to the roll-out of its marketing cam-
paigns. Because each of these activities is supported
by a different software tool, altogether, eight tools
have to be built in such a way that information made
available by one tool may be used by others.
Figure 1 presents the network of activities con-
cerning the development of the software tools. Ta-
ble 1 relates each activity to the roles they play in
the project. It should be noted that GIL is a library
of software components that allows the graphic inter-
face of the whole software to have a common visual
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS - A Branch & Bound Approach
165

identity. Also, to keep the number of arrows in the
network small, many of the dependencies that hold
among software tools are indirectly represented by a
path going from one tool to the other. For example,
the development of all software tools depends upon
the development of the graphical interface library. As
a result, there is a path going from GIL to all the other
tools.
In the course of time, tough competition in the
furniture business has brought down the company’s
annual profit. As a result, due to lack of financial
resources, only one tool may be under development
at any time. Moreover, high management has deter-
mined that every proposal for the development of new
software must be accompanied by a report showing its
total cost and expected financial benefits to business.
Aware of these restrictions the project manager
has decided that the system of software tools must
be developed in such a way that the project’s overall
value to business is maximized. Because this value
is highly dependent on the order in which the soft-
ware units are developed, the order that maximizes
the project’s net present value must be found.
3.1 Generating the Search Tree
Obviously, the development order that maximizes the
value to business is the one holding the highest NPV
among all possible valid sequences of software units.
In these circumstances, the branch & bound method
presents itself as the best option available and, as a
result, a search tree must be built.
Step 1: Initialization
The construction of the tree starts with the selection of
the Start node as the tree root. This node is identified
by the number zero. Figure 2 shows the contents of
node zero.
0
Start
UB:943
LB:357
Insertion order
Upper bound
Lower bound
Software tool
Values in thousands
of USA dollars
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
Insertion order
Upper bound
Lower bound
Software tool
Values in thousands
of USA dollars
Figure 2: The contents of node zero.
Note that the upper bound of node zero is the sum
of two values. The first, is the sum of the NPV of each
software unit (MMF or AE) belonging to the currently
known part of the development sequence of software
units. The second is the sum of the maximum NPV of
each unit belonging to the unknown part.
Because node zero is the only one in the tree, its
upper bound is the sum of the highest NPV of each
software unit throughout the whole project’s window
of opportunity, considering the precedence restric-
tions introduced in Figure 1. Therefore, the upper
bound of node zero, i.e. ub(0), is given by
ub(0) = npv(GIL, 9) + npv(PdS, 2)+ npv(PsS, 4)+
npv(Pc, 3) + npv(CD, 4) + npv(LP, 5)+
npv(SC, 5) + npv(CP, 6) + npv(CLM, 9)
= −42+ 134+ 157+ 87+ 71+ 11+ 53+
30+ 441
= $943
It should be noted that in formula the highest NPV
of unit Pc throughout the window of opportunity is
$87, and not $115 as one could expect. This happens
because the precedence restrictions introduced in Fig-
ure 1 do not allow Pc to be developed until the third
period.
The lower bound of node zero is the sum of the
lowest NPV of each software unit throughout the win-
dow of opportunity from the earliest period in which
each unit may be developed, considering the prece-
dence restrictions introduced in Figure 1. Therefore,
lb(0) = vpl(GIL, 1) + vpl(PdS, 9) +vpl(PsS, 9)+
vpl(Pc, 9) + vpl(CD, 9) + vpl(LP, 9)+
vpl(SC, 9) + vpl(CP, 9) + vpl(CLM, 9)
= −49+ 15+ 31+ 11− 10− 5− 71−
6+ 441
= $357
Observe that, in the worst case, to calculate both
the upper and lower of a node one has to visit all el-
ements of Table 3. Therefore, these value can always
be obtained in a polynomial time.
Step 2: Doing the initial branch
The search for the sequence of software units that
maximizes the project’s NPV goes on with the inser-
tion, in the search tree, of the nodes that corresponds
to the units that may be developed in the next period.
In this case, the choice is obvious, given that node
zero is the only node in the tree and GIL is the only
tool that may be developed immediately after. Figure
3 shows the search tree after the insertion of node 1,
corresponding to the GIL unit. The calculation of its
upper and lower bounds are done as described in Step
1.
Step 6: Selecting a node to branch
The search goes on according to the steps already de-
scribed until the tree reaches the state presented in
Figure 4 and a decision must be made: which node
should be branched?
At this point, several possibilities are available.
For example, one may choose the node with the high-
est upper bound, the one with highest lower bound,
or even the one with the highest average between its
ICEIS 2008 - International Conference on Enterprise Information Systems
166
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
Figure 3: The contents of node one.
lower and upper bound. In the absence of hard evi-
dence on which criteria is the best, a heuristic has to
be established. In this case, throughout the building of
the whole search tree, the algorithm always opt for the
node with the highest upper bound. Therefore, node
4 is selected for branching.
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
2 PdS
UB:935
LB:476
2 PdS
UB:935
LB:476
2 PdS
UB:935
LB:476
3 Pc
UB:935
LB:552
3 Pc
UB:935
LB:552
3 Pc
UB:935
LB:552
5 CD
UB:873
LB:633
5 CD
UB:873
LB:633
5 CD
UB:873
LB:633
4 PsS
UB:919
LB:678
4 PsS
UB:919
LB:678
4 PsS
UB:919
LB:678
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
Figure 4: Search tree when node 4 is selected for branching.
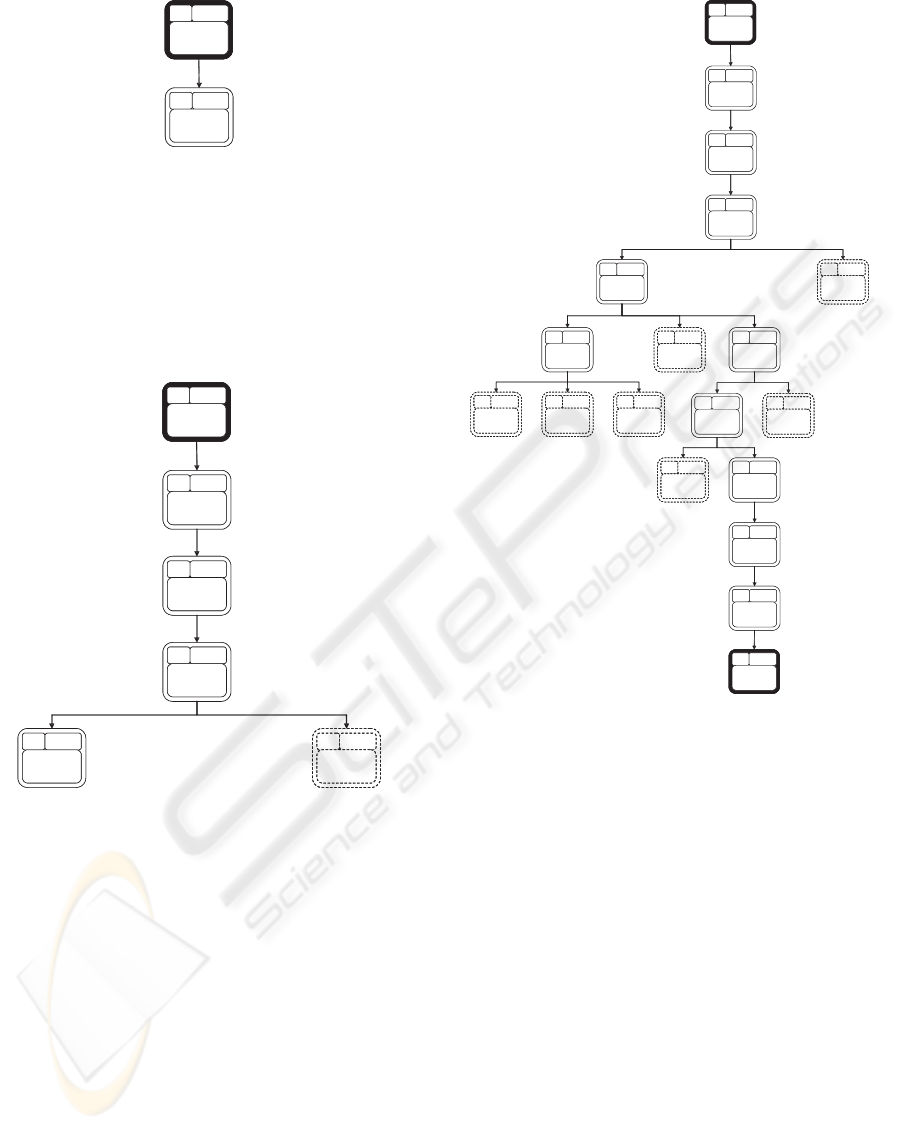
Step 13: Identifying the optimal solution
The search proceeds until the tree achieves the state
described in Figure 5.
At this point, there is no node that has an upper
bound that is higher than the lower bound of node
18, which cannot be branched. Therefore, the search
stops, and the path to node 18 corresponds to the
sequence that maximizes the NPV of the software
project, i.e. Start → GIL → PdS → Pc → PsS →
SC → CD → CP → LP → CLM → End, which yields
an NPV of $878.
It is important to observe that many nodes are
not branched during the search process. For exam-
ple, node 5 is never branched. This happens for two
reasons. First, while being considered for branching,
its upper bound is never the highest. Second, when
node 15 is inserted into the tree, the upper bound of
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
1 GIL
UB:935
LB:357
2 PdS
UB:935
LB:476
2 PdS
UB:935
LB:476
2 PdS
UB:935
LB:476
3 Pc
UB:935
LB:552
3 Pc
UB:935
LB:552
3 Pc
UB:935
LB:552
5 CD
UB:873
LB:633
5 CD
UB:873
LB:633
5 CD
UB:873
LB:633
4 PsS
UB:919
LB:678
4 PsS
UB:919
LB:678
4 PsS
UB:919
LB:678
6 CD
UB:882
LB:743
6 CD
UB:882
LB:743
6 CD
UB:882
LB:743
8 SC
UB:886
LB:803
8 SC
UB:886
LB:803
8 SC
UB:886
LB:803
7 LP
UB:858
LB:694
7 LP
UB:858
LB:694
7 LP
UB:858
LB:694
13 CP
UB:847
LB:778
13 CP
UB:847
LB:778
13 CP
UB:847
LB:778
12 SC
UB:866
LB:835
12 SC
UB:866
LB:835
12 SC
UB:866
LB:835
11 LP
UB:839
LB:754
11 LP
UB:839
LB:754
11 LP
UB:839
LB:754
9 CD
UB:882
LB:850
9 CD
UB:882
LB:850
9 CD
UB:882
LB:850
10 LP
UB:858
LB:814
10 LP
UB:858
LB:814
10 LP
UB:858
LB:814
15 CP
UB:878
LB:874
15 CP
UB:878
LB:874
15 CP
UB:878
LB:874
14 LP
UB:870
LB:858
14 LP
UB:870
LB:858
14 LP
UB:870
LB:858
16 LP
UB:878
LB:878
16 LP
UB:878
LB:878
16 LP
UB:878
LB:878
17 CLM
UB:878
LB:878
17 CLM
UB:878
LB:878
17 CLM
UB:878
LB:878
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
0
Start
UB:943
LB:357
18
End
UB:878
LB:878
18
End
UB:878
LB:878
18
End
UB:878
LB:878
Figure 5: The search tree generated by the branch & bound
method.
node 5 (which is the highest value that a sequence
of units that starts with GIL → PdS → Pc → CD may
have)is lower than the lowerbound of node 15 (which
is the lowest value that a sequence that starts with
GIL → Pds → Pc → PsS → SC → CD → CP may re-
turn). As a result, node 5 ceases to be considered for
branching.
4 THE BRANCH & BOUND
ALGORITHM
In formal terms , the branch & bound algorithm that
maximizes the NPV of a software project is described
as follows. Given
• A precedence graph of software units G(V
G
, E
G
),
composed of a set of software units V
G
, and the
precedence restrictions described in E
G
;
• A window of opportunity P and
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS - A Branch & Bound Approach
167

• A discount rate r.
The sequence S of software units v
i
∈ V
G
that yield
the highest NPV is found by the following algorithm:
Ω
T
← {Start}; Θ
T
←
/
0; Q ← {Start};
Repeat :
N ← q ∈ Q, such that ub(q) =
Maximum({ub(q
′
)|q
′
∈ Q}),
Ω
T
← Ω
T
∪ eligible(N),
Θ
T
← Θ
T
∪ {(N, e)|e ∈ eligible(N)},
MaxLB ← Maximum({lb(v)|v ∈ Ω
T
}),
Q ← {v ∈ Ω
T
|v ∈ (Q− {N}) ∪ eligible(N) ∧
ub(v) ≥ MaxLB},
Until Q =
/
0;
S ← path to(N).
where:
• S is the best solution among the nodes in Q;
• Ω
T
is the set of nodes in the search tree;
• Θ
T
is the set of edges connecting search tree
nodes;
• MaxLB is the highest lower bound so far; and
• Q is the list of candidate nodes.
4.1 The Upper Bound Heuristic
The upper-bound function ub(n ∈ Ω
T
) → R returns
the maximum NPV that a development sequence of
software units may yield considering the known part
of the sequence, i.e. the sequence that goes from the
tree root to node n.
ub(n) ←
∑
npv(s
i
, i) such that s
i
∈ path to(n)+
∑
npvMax(v
j
, when(n, v
j
)) such that
v
j
∈ (V
G
− {v
k
|v
k
∈ path to(n)})
4.2 The Lower Bound Heuristic
The lower bound function lb(n ∈ Ω
T
) → R returns
the minimum NPV that a development sequence of
software units may yield considering the known part
of the sequence, i.e. the sequence that goes from the
tree root to node n.
lb(N) ←
∑
npv(s
i
, i) such that s
i
∈ path to(n)+
∑
npvMin(v
j
, when(n, v
j
)) such that
v
j
∈ (V
G
− {v
k
|v
k
∈ path to(n)})
4.3 Auxiliaries Functions
The branch & bound method also make use of the fol-
lowing functions:
• eligible(N ∈ Ω
T
) → PV
G
that returns the set of
possible immediate successors of a node n in the
search tree.
• path to(N ∈ Ω
T
) → SeqV
G
that returns the se-
quence of software units that leads to the node N
of the search tree.
• when(v
i
∈ V
G
, n ∈ Ω
T
) → P that returns the earli-
est period in which a software unit v
i
may be de-
veloped, considering the sequence that goes from
the tree root to n.
5 DISCUSSION
At the outset of this article the authors undertook to
successfully present a branch & bound approach that
allows managers to determine the optimum order for
the development of a network of software units. Bel-
low we answer some key questions about the implica-
tions of the method to software development and the
deployment of business strategy.
5.1 Why should a Branch & Bound
Method be used to Maximize the
NPV of a Software Project?
The number of possible development sequences of
a network of software units tends to grow exponen-
tially according to the number of MMFs and AEs into
which a software project is divided, making it difficult
to find their optimum implementation order in a fea-
sible time. Consequently, the search for the optimum
order benefits from the use of heuristic methods such
as the branch & bound that, in most cases, does not
need to enumerate all possible sequences of software
units to indicate the optimum (Liberti, 2003).
5.2 What does this Method offer that
the IFM does not?
There are two major advantages in using the branch
& bound method instead of the IFM. The first is that
it ensures that an optimal solution to a problem is al-
ways found, while the IFM may provide inferior re-
sults with no warning. In projects that cost millions of
US dollars, even a small difference from the optimal
solution may lead to a loss of a substantial amount
of money. Losses of this magnitude may hamper
business competitiveness,allowing the growthof rival
companies. The second advantage is that this method
can be applied to projects that present multiple depen-
dencies among its software units, which is frequently
the case in real-world software projects.
ICEIS 2008 - International Conference on Enterprise Information Systems
168

5.3 Does the Branch & Bound Method
allow for Parallel Development?
No, it does not. Actually, building a branch & bound
algorithms that deals with the parallel development
of MMFs and AEs is still an open problem. How-
ever, the vast majority of software projects in the real
world are run by small companies that do not have the
personnel nor the necessary resources to use parallel
development (Harris et al., 2007).
5.4 What is the Expected Effect of the
Branch & Bound Method on
Software Development?
Because of the tough competition that are currently
being experienced in many different markets, nowa-
days many companies are offshoring the development
of software, creating a healthy competitive environ-
ment in which software companies compete against
each other for contracts. Obviously, proposals that
maximize the financial value of a software project
provide a better competitive position in regard to
those that have adopted a more traditional view of the
software development.
Moreover, it is important to keep in mind that the
smaller investment in the development of a software
project provided by the branch & bound method fa-
vors the development of other projects that could not
be executed otherwise. All of this, favor the existence
of companies that are more efficient and better pre-
pared to compete in the world market.
6 CONCLUSIONS
This article presented a branch & bound method that
identifies the development plan that maximizes the
business value of a software project. The method al-
ways finds the best solution and does not imposes un-
reasonable limitations to the precedence relations that
may exist among the software units, facilitating the
development of complex software projects from a rel-
atively small investment.
REFERENCES
Abacus, A., Barker, M., and Freedman, P. (2005). Us-
ing test-driven software development tools. Software,
IEEE, 22(2):88–91.
Denne, M. and Cleland-Huang, J. (2004a). The incremental
funding method: data-driven software development.
IEEE Software, 21(3):39–47.
Denne, M. and Cleland-Huang, J. (2004b). Software
by Numbers - Low-Risk, High-Return Development.
Prentice Hall.
Denne, M. and Cleland-Huang, J. (2005). Financially in-
formed requirements prioritization. In Roman, G.-C.,
Griswold, W., and Nuseibeh, B., editors, 27
th
inter-
national conference on Software Engineering, pages
710–711, St. Louis, MO, USA. ACM.
Fabozzi, F. J., Davis, H. A., and Choudhry, M. (2006). In-
troduction to Structured Finance. John Wiley.
Gross, J. L. and Yellen, J. (2005). Graph Theory and Its
Applications. Chapman & Hall and CRC, 2
nd
edition.
Harris, M., Aebischer, K., and Klaus, T. (2007). The
whitewater process: Software product development in
small IT businesses. Communications of the ACM,
50(5):89–93.
Helo, P., Hilmola, O.-P., and Maunuksela, A. (2004). Man-
aging the productivity of product development: a sys-
tem dynamics analysis. International Journal of Man-
agement and Enterprise Development, 1(4):333–344.
Highsmith, J. (2002). Agile Software Development Ecosys-
tems. Addison-Wesley.
Hillier, F. S. and Lieberman, G. J. (2001). Introduction to
operations research. McGraw-Hill, New York, NY,
7
th
edition.
Hubbard, D. W. (2007). How to Measure Anything: Finding
the Value of “Intangibles” in Business. John Wiley.
Jorgenson, D. W., Ho, M. S., and Stiroh, K. J. (2003).
Growth of us industries and investments in informa-
tion technology and higher education. Economic Sys-
tems Research, 15(3):279–325.
Lam, H. (2004). New design-to-test software strategies ac-
celerate time-to-market. In 29
th
International Elec-
tronics Manufacturing Technology Symposium, pages
140–143, San Jose, CA, USA. IEEE.
Liberti, L. (2003). Optimization and Optimal Control, chap-
ter Comparison of Convex Relaxations for Monomials
of Odd Degree, pages 165–174. Computers and Op-
erations Research. World Scientific.
McManus, J. C. (2003). Risk Management in Software De-
velopment Projects. Elsevier.
Nord, R. and Tomayko, J. (2006). Software architecture-
centric methods and agile development. Software,
IEEE, 23(2):47–53.
Rashid, A., Moreira, A., and Ara´ujo, J. (2003). Modu-
larisation and composition of aspectual requirements.
In Proceedings of the 2
nd
International Conference
on Aspect-oriented Software Development, pages 11
– 20, Boston, Massachusetts, USA. ACM.
Steindl, C. (2005). From agile software development to
agile businesses. In Matos, J. S. and Crnkovic, I.,
editors, 31
st
EUROMICRO Conference on Software
Engineering and Advanced Applications, pages 258–
265, Porto, Portugal. Porto University.
Whittle, R. and Myrick, C. B. (2005). Enterprise Business
Architecture. Auerbach.
MAXIMIZING THE BUSINESS VALUE OF SOFTWARE PROJECTS - A Branch & Bound Approach
169
