
K-NN: ESTIMATING AN ADEQUATE VALUE FOR PARAMETER K
Bruno Borsato, Alexandre Plastino
∗
Department of Computer Science, Fluminense Federal University, Niter´oi, Brazil
Luiz Merschmann
†
Department of Exact and Applied Sciences, Ouro Preto Federal University, Jo˜ao Monlevade, Brazil
Keywords:
k-NN, classification, data mining.
Abstract:
The k-NN (k Nearest Neighbours) classification technique is characterized by its simplicity and efficient per-
formance on many databases. However, the good performance of this method relies on the choice of an
appropriate value for the input parameter k. In this work, we propose methods to estimate an adequate value
for parameter k for any given database. Experimental results have shown that, in terms of predictive accuracy,
k-NN using the estimated value for k usually outperforms k-NN with the values commonly used for k, as well
as well-known methods such as decision trees and naive Bayes classification.
1 INTRODUCTION
Classification is one of the most important tasks of
data mining and machine learning areas (Han and
Kamber, 2005; Witten and Frank, 2005), therefore
there are innumerable projects and research groups
dealing with it. The construction of precise and com-
putationally efficient classifiers for large databases, in
terms of number of instances and attributes, is one of
the greatest challenges arisen in these research areas.
The intense interest on this subject stimulated many
researchers to propose techniques for the construction
of classifiers, such as decision trees (Quinlan, 1986),
naive Bayes (Duda and Hart, 1973), Bayesian net-
works (Heckerman, 1997), neural networks (Haykin,
1994), k-NN (k Nearest Neighbours) (Aha, 1992),
support vector machines (Vapnik, 1995) and others.
The k-NN (k Nearest Neighbours) technique was
initially analyzed in (Fix and Hodges, 1951), being
its application in classification problems firstly per-
formed in (Johns, 1961). However, only after the re-
sults presented in (Aha, 1992), this approach became
popular as a classification method.
The basic idea of the k-NN method is very sim-
ple. It uses some distance metric to search the training
∗
Work sponsored by CNPq research grants 301228/06-0
and 476848/07-5.
†
Work sponsored by CNPq PhD scholarship.
database for the k closest neighbours of the instance
whose classification is desired, attributing the most
frequent class among its k neighbours to it. How-
ever, the good performance of this method relies on
the choice of an appropriate value for the input pa-
rameter k.
In this work, we propose and explore some strate-
gies to identify, for a given database, an adequate
value for k, that is, one that maximizes the perfor-
mance of k-NN for this database.
Previous works approached related problems and
solutions. In (Wettschereck and Dietterich, 1994),
four variations of the k-NN method were presented.
These variations determine the value of parameter k
to be used in the classification of a novel instance
through the evaluation of its neighbourhood. These
strategies presented a performance similar to the clas-
sical k-NN for 12 databases usually employed in clas-
sification tasks, and have shown to be superior to the
k-NN for three databases generated by the authors.
In (Wang, 2003), the question of the choice of pa-
rameter k for k-NN was discussed and an approach
that tries to improve the performance (accuracy) of
classical k-NN was proposed. Differently from k-NN,
that uses a single set of closest neighbours to classify
a novel instance, the proposal performs the classifi-
cation considering many sets of closest neighbours.
This proposal, named nokNN, have shown that when
459
Borsato B., Plastino A. and Merschmann L. (2008).
K-NN: ESTIMATING AN ADEQUATE VALUE FOR PARAMETER K.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 459-466
DOI: 10.5220/0001686104590466
Copyright
c
SciTePress

the number of employed sets of closest neighbours in-
creases, the accuracy of the classifier also increases,
stabilizing after a determined number of sets. Experi-
mental results have shown that the accuracy (after sta-
bilization) of the nokNN was slightly superior to the
classical k-NN (when k varies from 1 to 10).
In (Guo et al., 2003), a classification method
named kNN Model was proposed. Aiming at reduc-
ing the databases, this method builds a model from the
training data that is used on the classification of novel
instances. The model is composed by a set of repre-
sentative instances from the original database and by
some information related to their arrangement in the
database. From an evaluation that used six databases,
the results have shown that the performance (average
accuracy for the six databases) of this proposal was
equivalent to k-NN (k = 1, 3, and 5) and superior
to C5.0 (Quinlan, 1993). Besides, it was shown that
kNN Model reduces the number of data tuples in the
final model, with a 90.41% reduction rate on average.
In (Angiulli, 2005), it was presented an algorithm,
named FCNN (Fast Condensed Nearest Neighbour),
to reduce the training database to be used by the tech-
nique known as the nearest neighbour decision rule.
Basically, the reduction of the original database is ob-
tained by removing irrelevant instances, that is, the
ones that do not affect the classifier accuracy. When
compared to other databases reduction algorithms,
FCNN has shown itself more efficient in terms of scal-
ability and database reduction rate.
In this work, initially, we show that the identifi-
cation of an appropriate value for parameter k can be
achieved, for small databases, through a previous and
exhaustive evaluation of all possible values of k. This
approach is computationally tractable for not large
databases and improves the k-NN performance when
compared to techniques such as decision trees and
naive Bayes classification. Afterwards, we adapt the
technique to estimate a value for k on larger databases
for which the exhaustive approach is generally pro-
hibitive due to high computational costs.
The remainder of this article is organised as fol-
lows. Section 2 presents the exhaustive approach for
determining a value for k. Sections 3 and 4 present
two different proposals to overcome the high compu-
tational cost of the exhaustive approach and also the
obtained experimental results. In Section 5, final con-
siderations are made.
2 EXHAUSTIVE APPROACH
The exhaustive strategy to identify an appropriate
value for parameter k will be presented in this section.
Let C = {C
1
,C
2
,C
3
, . . . , C
m
} be the set of classes
and D = {d
1
, d
2
, d
3
, . . . , d
n
} be the set of instances
belonging to a database D. Each instance d
i
∈ D,
1 ≤ i ≤ n, is labeled with a class C
j
∈C, 1 ≤ j ≤ m.
Given the database D, the idea of the exhaustive pro-
cedure is to classify each instance of D using all pos-
sible values of k, and then return the value of k which
correctly classifies the largest number of instances.
Let hits(D, x) be the number of instances from D
correctly classified using k-NN when k = x. The value
z, 1 ≤ z < n, will be returned by the exhaustive proce-
dure, being considered the appropriate value for pa-
rameter k, if and only if hits(D, z) ≥ hits(D, y) for
all y, 1 ≤ y < n, y 6= z. If more than one value in
[1, n−1] correctly classifies the largest number of in-
stances, the lowest one will be returned.
The detailed functioning of the exhaustive ap-
proach is presented in Algorithm 1. The loop from
lines 1 to 11 represents, for each instance d
i
, the ex-
ecution of the k-NN strategy for all possible values
of parameter k. The inner loop from lines 2 to 4
calculates N
i
, which represents the neighbourhood of
d
i
. It is a list of pairs (dist(d
i
, d
j
),C
j
) sorted by dis-
tance (dist(d
i
, d
j
)) in ascending order. The distance
between instances d
i
and d
j
is a measure of their sim-
ilarity. Though many distance metrics exist (Kaufman
and Rousseeuw, 1990), Euclidean distance is usually
employed along with k-NN. Therefore, this metric is
also adopted in this work.
The inner loop from lines 5 to 10 evaluates which
values of k achieve a correct classification for each
instance d
i
. The number of correct classifications for
each value of k is stored on vector kVector. Each po-
sition of the vector is associated with a value for k.
From lines 12 to 18, the best value for parameter
k is obtained from the vector kVector. The position
with the highest count is the most appropriate choice
for parameter k, that is, the value of k that achieved
the biggest number of correct classifications. Finally,
on line 19, the procedure returns bestK.
2.1 Experimental Results
In order to evaluate the performance of the exhaustive
approach, many experiments have been carried out.
Performance was measured in terms of predictive
accuracy. The method adopted for estimating the pre-
dictive accuracy was 10-fold cross-validation (Han
and Kamber, 2005). In this way, each database was
randomly divided in 10 partitions of the same size
and the evaluation was conducted in 10 iterations.
In each iteration, the test database consists of one
partition, while the other nine constitute the training
database. Accuracy is then obtained by dividing the
ICEIS 2008 - International Conference on Enterprise Information Systems
460

Table 1: Exhaustive approach predictive accuracy comparison.
Datasets Inst,Attrib Exhaustive appr. 1NN 3NN 5NN
√
n J48 Bayes
Classes k acc(%) T(s) acc(%) acc(%) acc(%) acc(%) acc(%) acc(%)
Adult 30162,14,2 66 83.15 7826.0 78.92 81.44 82.29 82.92 85.73 83.64
Anneal 898,38,5 1 98.98 10.7 98.98 97.09 97.07 91.61 98.64 95.71
Austr 690,14,2 9 86.99 2.8 81.54 85.62 86.54 85.61 85.65 85.88
Auto 205,25,6 1 74.98 0.4 74.98 66.49 62.88 57.76 80.49 63.85
Chess 3196,36,2 3 97.10 113.2 96.62 97.10 96.37 90.94 99.38 87.70
Cleve 303,13,5 2 58.71 0.5 54.22 55.58 57.89 56.01 51.95 55.18
Credit 690,15,2 102 87.12 2.9 81.54 85.20 86.07 86.19 85.62 86.07
German 1000,20,2 11 74.28 7.6 72.10 72.75 73.22 72.78 71.21 74.30
Glass 214,9,6 1 68.93 0.2 68.93 69.11 65.05 61.22 68.64 70.28
Hdigit 10992,16,10 1 99.35 1027.3 99.35 99.35 99.24 95.40 96.50 87.64
Heart 270,13,2 54 82.85 0.4 76.11 79.11 80.11 81.19 78.41 82.52
Hepat 155,19,2 13 84.32 0.2 81.42 79.35 81.48 83.16 78.71 84.06
Horse 368,22,2 162 82.42 1.2 72.66 78.94 81.06 81.30 85.11 79.59
Hypo 3163,25,2 1 97.39 96.7 97.39 97.20 97.29 95.71 99.28 98.48
Ionosp 351,34,2 2 89.40 1.5 86.58 85.78 84.96 82.79 89.09 89.52
IrisP 150,4,3 6 96.60 0.1 95.33 95.13 95.67 96.60 94.40 93.07
Isegm 2310,19,7 1 97.45 39.3 97.45 96.19 95.32 90.35 96.91 91.23
LaborR 57,16,2 1 93.51 0.1 93.51 91.05 91.75 90.35 79.30 87.54
Landsat 6435,36,6 3 90.99 580.5 90.35 90.99 90.86 86.12 86.37 82.05
LetterR 20000,16,26 1 95.98 3514.0 95.98 95.65 95.54 80.97 87.99 74.02
Lymph 148,18,4 3 84.59 0.2 80.61 84.59 83.99 81.96 76.35 84.59
Mushr 8124,22,2 1 100 479.3 100 100 100 98.92 100 95.75
Nurse 12960,8,5 1 97.99 615.0 97.99 97.99 97.99 96.07 97.12 90.30
PimaI 768,8,2 33 75.22 2.3 70.20 73.52 73.67 74.51 74.24 75.64
Sflare 1066,12,6 13 74.22 5.2 72.23 72.98 73.29 73.94 74.09 74.37
Shuttle 5800,9,6 1 99.66 185.9 99.66 99.48 99.36 98.43 99.84 99.13
Sick 3772,29,2 5 96.24 155.6 96.23 96.28 96.24 94.39 98.72 97.15
Sonar 208,60,2 1 86.73 0.9 86.73 83.08 82.40 68.61 73.75 76.59
SoybL 683,35,19 2 92.25 5.4 92.23 91.96 90.73 73.27 91.33 92.75
SoybS 47,35,4 1 100 0.1 100 100 100 100 97.66 100
Splice 3190,61,3 566 93.67 188.6 74.42 78.12 79.69 89.37 94.13 95.40
T-t-t 958,9,2 1 98.95 3.2 98.95 98.95 98.95 77.29 84.83 69.80
VehicS 846,18,4 6 70.43 5.2 69.80 69.76 69.91 66.71 72.41 60.73
Voting 435,16,2 3 93.33 1.0 92.30 93.33 93.49 91.33 96.53 90.16
Wavef 5000,40,3 110 85.20 324.8 72.92 77.72 79.94 84.62 75.43 80.04
Wbreas 699,9,2 1 95.61 1.6 95.61 95.02 94.86 92.73 94.82 97.25
WineR 178,13,3 13 97.30 0.2 94.94 96.24 95.28 97.30 93.65 98.54
Yeast 1484,8,10 24 58.92 8.8 52.11 55.03 56.76 58.36 55.61 57.71
Zoo 101,17,7 1 95.84 0.1 95.84 92.67 90.89 88.91 92.18 92.18
Average 88.12 390.0 85.56 86.05 86.10 83.48 85.69 84.11
Algorithm 1 Exhaustive approach.
Input: D
Output: bestK
1: for each d
i
∈ D do
2: for each d
j
∈ D (such as j 6= i) do
3: insert into N
i
the pair (dist(d
i
, d
j
),C
j
);
4: end for
5: for k = 1 to n−1 do
6: classification ⇐ most frequent class among the
k first pairs of list N
i
;
7: if (classification = C
i
) then
8: kVector[k] + +;
9: end if
10: end for
11: end for
12: biggestFreq ⇐0;
13: for p = 1 to n−1 do
14: if (kVector[p] > biggestFreq) then
15: bestK ⇐ p;
16: biggestFreq ⇐kVector[p];
17: end if
18: end for
19: return bestK;
number of corrected classified instances (among all
iterations) by the total number of instances belong-
ing to the database. The same partitions have been
employed on the evaluation of all the presented tech-
niques.
Experiments were carried out on 39 databases.
The employed databases are of public domain and can
be found on the UCI Machine Learning Repository
(Newman et al., 1998). They vary on size (number of
instances and number of attributes), content and ori-
gin.
Results have been compared to the k-NN itself
with fixed values for parameter k, as well as to well-
known methods such as decision tree and naive Bayes
classification. The results of the two later methods
were obtained using the algorithms J48 and Naive-
Bayes, respectively, present in the Weka
3
tool (Witten
and Frank, 2005). J48 was run with default parame-
ters and NaiveBayes with supervised discretisation.
The experimental results, reported on Table 1,
have shown that the exhaustive approach excels on
estimating an adequate value for parameter k. The
databases used are reported on the first column. The
next column contains the number of instances, at-
tributes and classes of each database. The three fol-
lowing columns show the best value for k, the ac-
curacy result achieved using this value and the CPU
3
http://www.cs.waikato.ac.nz/ml/weka/
K-NN: ESTIMATING AN ADEQUATE VALUE FOR PARAMETER K
461

Table 2: Exhaustive approach comparison to other tech-
niques.
1-NN 3-NN 5-NN
√
n-
NN
J48 Bayes
better 23 28 33 36 28 25
equal 16 9 5 3 1 2
worse 0 2 1 0 10 12
time
4
in seconds taken to estimate it. Columns 6 to 9
report the accuracy results of the k-NN (k = 1, 3, 5,
and
√
n, where n is the total number of instances in
each database). (Duda et al., 2000) suggest the value
√
n as a good value for k. The last two columns re-
port the results obtained with the methods decision
tree (J48) and naive Bayes classification (Bayes).
Each value in bold face in Table 1 represents the
highest accuracy result obtained for each database
among all techniques employed. The exhaustive ap-
proach was the one that achieved the highest accuracy
most times. It presented the best results for 21 out
of the 39 databases. The other techniques ranked as
following: 1-NN and Bayesian classification (11 best
results), decision tree (10), 3-NN (7), 5-NN (4), and
√
n-NN (2).
The last line of Table 1 presents the average accu-
racy results for all the techniques. The exhaustive ap-
proach obtained the highest average accuracy result,
achieving 88.12%. The other techniques ranked as
following: 5-NN (86.10%), 3-NN (86.05%), decision
tree (85.69%), 1-NN (85.56%), Bayesian classifica-
tion (84.11%), and
√
n-NN (83.48%).
Table 2 presents a one-to-onecomparison between
the results obtained by the exhaustive approach and
by the other techniques employed on this experiment.
For example, among the 39 databases, the exhaustive
approach achieved better accuracy results than the 1-
NN technique on 23 databases; these two techniques
achieved an equal accuracy result on 16 databases;
and the exhaustive approach achieved a worse accu-
racy result for none of the databases. The interpreta-
tion of the other columns is analogous. These results
show that the exhaustive approach performed better
than all other strategies.
Analysing the CPU time taken to determine the
best value of k, reported on Table 1, it is noticeable
that larger databases, in terms of number of instances,
demand a considerably greater amount of time to de-
termine the best value of k using the exhaustive ap-
proach. The two largest databases, Adult and LetterR,
demanded 7826.0 and 3514.0 seconds, respectively,
while smaller databases demanded less than a second.
4
All reported experiments have been carried out on a
Pentium IV 2,8 GHz, 512Mbytes RAM
Therefore, the shortcoming of the exhaustive ap-
proach is that it is time-consuming, making it infea-
sible to be used with large databases. To overcome
that, the following sections introduce two approaches
that aim at reducing the number of database instances
evaluated by the exhaustive technique, making it fea-
sible to be used with larger databases.
3 CLUSTERING SAMPLING
This section will introduce the first of two approaches
used to obtain the reduced set of database instances.
The reduction is intended to make the exhaustive ap-
proach, presented on the previous section, feasible in
terms of computational time.
The goal of the sampling techniques proposed in
this work is to obtain a reduced and representative
subset of instances from the original database, called
set of samples, in a way to reduce the high compu-
tational cost of the exhaustive approach when per-
formed over large databases. Each instance of the
set of samples must represent a group of instances
(of same class) of the original database. Preliminary
results using these ideas were presented in (Borsato
et al., 2006).
The clustering sampling strategy consists on the
execution of a clustering algorithm over each set of
instances of same class on the original database. Af-
terwards, from each obtained cluster, a representative
instance will be chosen and inserted in the set of sam-
ples.
The KMeans algorithm (MacQueen, 1967) is used
to cluster the instances of the same class belonging
to the original database. The algorithm is performed
separately for each class and will maintain proportion
among classes on the set of samples. After the cluster-
ing process is completed, the instances that are closest
to the resultant centroids will compose the set of sam-
ples. The set of samples, though, is used only for the
estimation of parameter k. The classification task is
performed on the full original database.
Let SS = {d
1
, d
2
, d
3
, . . . , d
r
}be the set of instances
belongingto the set of samples SS. The exhaustiveap-
proach over the set of samples is presented on Algo-
rithm 2. This algorithm is very similar to Algorithm 1.
The difference relies on line 1. Instead of a loop in-
volving all instances of the original database, just the
instances belonging to the set of samples (generated
after the clustering process) will be considered. It is
important to notice that the loop starting on line 2 re-
mains unaltered. In this way, all instances belonging
to the set of samples have their distances to all other
instances (in the original database) calculated. The
ICEIS 2008 - International Conference on Enterprise Information Systems
462

rest of the process remains the same (lines 12 to 19
were omitted).
Algorithm 2 Exhaustive approach over the set of
samples.
Input: D, SS
Output: bestK
1: for each d
i
∈ SS do
2: for each d
j
∈ D (such as j 6= i) do
3: insert into N
i
the pair (dist(d
i
, d
j
),C
j
);
4: end for
5: for k = 1 to n−1 do
6: classification ⇐ most frequent class among the
k first pairs of list N
i
;
7: if (classification = C
i
) then
8: kVector[k] + +;
9: end if
10: end for
11: end for
3.1 Experimental Results
Since it is not necessary to perform a reduction on
small databases, experimental results were carried
out only on databases with 1000 or more instances,
among those employed on experiments described on
Section 2.1. Varied reduction rates were employed
when testing the approach’s predictive accuracy. Re-
duction rates were always defined as a percentage
of the total number of instances presented in the
databases. The databases were reduced to 1, 3, 5, 10,
15, and 20 percent of their original size.
The experimental results for this approach are re-
ported in Tables 3 and 4. In Table 3, the first col-
umn contains the names of the databases used on
this study. The second column shows the number
of instances, attributes and classes for each database.
From columns 3 to 6, the results for the reduction to
1% are presented as follows: the estimated k, the ac-
curacy achieved with this k value, the CPU time taken
to estimate it, and the reduction achieved on compu-
tational time when compared to the results presented
on Table 1 (the symbol ‘−’ indicates that no reduction
was achieved). Similarly, columns 7 to 10 present the
results for the reduction to 3%, and the results for the
reduction to 5% are presented in columns 11 to 14.
Table 4 is organised in the same way as Table 3, pre-
senting the results for reductions to 10, 15, and 20%.
The bold face values represent the highest accuracy
result for a particular database among all reduction
rates evaluated.
Analysing the results from Tables 3 and 4, it is
possible to notice that the smaller the reduction rates
are, the average accuracy results tend to be greater.
Indeed, when working with a smaller reduction rate,
that is, a greater part of the original database, the
results tend to approximate those that would be ob-
tained if no reduction was employed. When the low-
est reduction (to 20%) was employed, an average ac-
curacy result of 89.85% was obtained. When no re-
duction is performed, the average accuracy result is
equal to 90.10%.
Even for the value of k estimated employing the
highest reduction rate (1%), the average accuracy re-
sult (89.52%) outperformed those from all the other
methods evaluated. Table 5 reports the results of those
methods for the databases employed on this study.
Again, the comparisons are made to the k-NN with k
= 1, 3, 5, and
√
n, to decision tree and to naive Bayes
classification.
For the majority of the databases, the intended re-
duction on computational time was achieved, main-
taining the quality of the accuracy results. For exam-
ple, the exhaustive approach took 3514.0 seconds to
determine the value of k to be used with the database
LetterR. When a reduction to 1% was employed, the
same value of k could be estimated in 50.2 seconds.
This represents a reduction of 98.57% on computa-
tional time, as presented in column 6 of Table 3.
The reduction on computational time presented
large variation among the different databases anal-
ysed. This variation is a consequence of the converg-
ing time required by the KMeans algorithm, which
depends on the characteristics of each database (num-
ber of instances, number of attributes, and spatial dis-
tribution, for example).
However,for databases like Adult, Hypo, and Sick
the computational time taken to estimate the value of
k, when compared to the computational time taken to
determine the value of k through the exhaustive ap-
proach, increased considering the reductions to 10%,
15%, and 20%. This increase on computational time
is due to the converging time required by the KMeans
algorithm. That was a motivation for the approach
presented on the following section, which aims at a
further reduction of the computational time, yet pre-
serving the accuracy results.
4 RANDOM SAMPLING
In this section, we will introduce another approach to
obtain the reduced subset of instances from the orig-
inal database (set of samples), called random sam-
pling. Its basic idea is to randomly choose instances
from the original databases to be present in the set of
samples.
Similarly to the clustering sampling approach pre-
sented on Section 3, random sampling aims at gener-
K-NN: ESTIMATING AN ADEQUATE VALUE FOR PARAMETER K
463
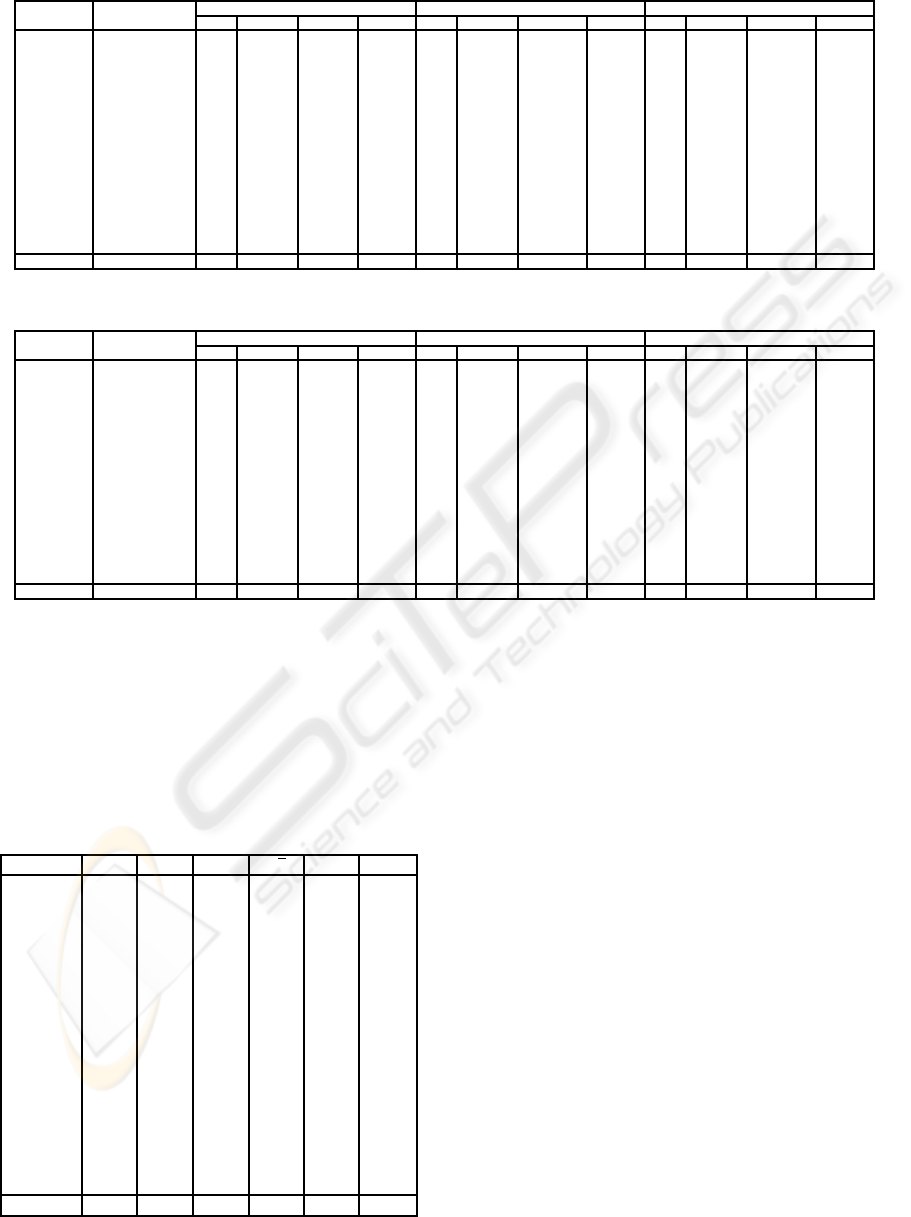
Table 3: Clustering Sampling predictive accuracy comparison (1/2).
Datasets Inst,Attrib, 1% 3% 5%
Classes k acc(%) T(s) red(%) k acc(%) T(s) red(%) k acc(%) T(s) red(%)
Adult 30162,14,2 49 83.12 899.0 88.51 73 83.19 2635.8 66.32 9 82.84 3685.8 52.90
Chess 3196,36,2 1 96.62 3.4 97.00 1 96.62 14.6 87.10 1 96.62 20.9 81.54
German 1000,20,2 9 74.08 0.6 92.11 1 72.10 1.4 81.58 1 72.10 2.1 72.37
Hdigit 10992,16,10 1 99.35 23.5 97.71 1 99.35 62.4 93.93 1 99.35 96.8 90.58
Hypo 3163,25,2 2 96.79 11.3 88.31 2 96.79 25.6 73.53 1 97.39 62.3 35.57
Isegm 2310,19,7 1 97.45 1.6 95.93 1 97.45 3.7 90.59 1 97.45 6.0 84.73
Landsat 6435,36,6 10 90.24 23.5 95.95 1 90.35 58.1 89.99 8 90.41 102.1 82.41
LetterR 20000,16,26 1 95.98 50.2 98.57 3 95.65 146.0 95.85 1 95.98 231.9 93.40
Mushr 8124,22,2 1 100 12.6 97.37 1 100 27.3 94.30 1 100 46.1 90.38
Nurse 12960,8,5 1 97.99 9.0 98.54 1 97.99 23.3 96.21 1 97.99 44.7 92.73
Sflare 1066,12,6 1 72.23 0.1 98.08 1 72.23 0.2 96.15 12 74.19 0.4 92.31
Shuttle 5800,9,6 2 99.55 6.2 96.66 2 99.55 20.6 88.92 9 99.28 31.6 83.00
Sick 3772,29,2 1 96.23 26.1 83.23 1 96.23 68.1 56.23 1 96.23 115.8 25.58
Splice 3190,61,3 223 92.85 11.4 93.96 581 93.67 28.4 84.94 581 93.67 69.7 63.04
Wavef 5000,40,3 34 84.06 35.1 89.19 33 84.12 53.1 83.65 22 83.42 87.7 73.00
Yeast 1484,8,10 4 55.71 0.4 95.45 20 58.69 0.8 90.91 32 58.46 1.3 85.23
Average 89.52 69.6 94.16 89.62 198.1 85.64 89.71 287.8 74.92
Table 4: Clustering Sampling predictive accuracy comparison (2/2).
Datasets Inst,Attrib, 10% 15% 20%
Classes k acc(%) T(s) red(%) k acc(%) T(s) red(%) k acc(%) T(s) red(%)
Adult 30162,14,2 121 83.11 8196.9 − 80 83.17 12074.8 − 107 83.12 14846.7 −
Chess 3196,36,2 2 96.69 45.1 60.16 3 97.10 53.0 53.18 2 96.69 86.4 23.67
German 1000,20,2 23 73.84 4.6 39.47 2 72.32 5.2 31.58 6 73.98 5.5 27.63
Hdigit 10992,16,10 1 99.35 186.5 81.85 1 99.35 249.0 75.76 1 99.35 331.4 67.74
Hypo 3163,25,2 7 97.19 105.5 − 4 97.15 168.3 − 9 97.20 194.3 −
Isegm 2310,19,7 1 97.45 8.4 78.63 1 97.45 10.8 72.52 1 97.45 14.2 63.87
Landsat 6435,36,6 5 90.86 179.7 69.04 3 90.99 270.7 53.37 1 90.35 307.9 46.96
LetterR 20000,16,26 1 95.98 447.6 87.26 1 95.98 651.9 81.45 1 95.98 879.1 74.98
Mushr 8124,22,2 1 100 121.0 74.75 1 100 222.4 53.60 1 100 331.2 30.90
Nurse 12960,8,5 1 97.99 116.1 81.12 1 97.99 207.9 66.20 1 97.99 338.7 44.93
Sflare 1066,12,6 19 74.17 0.8 84.62 19 74.17 1.1 78.85 3 72.98 1.5 71.15
Shuttle 5800,9,6 1 99.66 76.7 58.74 1 99.66 135.9 26.90 1 99.66 193.8 −
Sick 3772,29,2 5 96.24 276.7 − 1 96.23 316.4 − 1 96.23 381.1 −
Splice 3190,61,3 581 93.67 88.0 53.34 413 93.48 139.7 25.93 581 93.67 164.3 12.88
Wavef 5000,40,3 327 84.96 155.2 52.22 336 85.16 150.1 53.79 86 84.92 198.7 38.82
Yeast 1484,8,10 4 55.71 2.0 77.27 9 58.34 3.7 57.95 11 57.99 3.6 59.09
Average 89.80 625.7 50.43 89.91 916.3 31.21 89.85 1142.4 13.93
ating a set of samples so that the exhaustive approach
can be performed to estimate an adequate value for k
in feasible computational time. The difference is on
how the representatives belonging to the set of sam-
ples will be chosen. On random sampling, instead
of performing a clustering algorithm to help find-
ing these representatives, they will be selected ran-
Table 5: Other methods predictive accuracy comparison.
Databases 1-NN 3-NN 5-NN
√
n J48 Bayes
Adult 78.92 81.44 82.29 82.92 85.73 83.64
Chess 96.62 97.10 96.37 90.94 99.38 87.70
German 72.10 72.75 73.22 72.78 71.21 74.30
Hdigit 99.35 99.35 99.24 95.40 96.50 87.64
Hypo 97.39 97.20 97.29 95.71 99.28 98.48
Isegm 97.45 96.19 95.32 90.35 96.91 91.23
Landsat 90.35 90.99 90.86 86.12 86.37 82.05
LetterR 95.98 95.65 95.54 80.97 87.99 74.02
Mushr 100 100 100 98.92 100 95.75
Nurse 97.99 97.99 97.99 96.07 97.12 90.30
Sflare 72.23 72.98 73.29 73.94 74.09 74.37
Shuttle 99.66 99.48 99.36 98.43 99.84 99.13
Sick 96.23 96.28 96.24 94.39 98.72 97.15
Splice 74.42 78.12 79.69 89.37 94.13 95.40
Wavef 72.92 77.72 79.94 84.62 75.43 80.04
Yeast 52.11 55.03 56.76 58.36 55.61 57.71
Average 87.11 88.02 88.34 86.83 88.65 85.56
domly among the instances belonging to the original
database. After that, Algorithm 2 can be performed
the same way as presented on Section 3.
Proportion among classes is again respected. The
random process of choosing representatives is per-
formed on each class separately, in a way that it is
guaranteed that the reduced database has the same
class distribution as the original database.
4.1 Experimental Results
A study similar to the one introduced on Section 3.1
is presented here. The set of databases with 1000 or
more instances was employed. Also, the varied reduc-
tion rates (1%, 3%, 5%, 10%, 15%, and 20%) were
analysed.
Experimental results tables resemble the ones pre-
sented in Section 3.1. Table 6 and Table 7 are anal-
ogous to Table 3 and Table 4, respectively. They
present the accuracy results for the sampling reduc-
tion method, where the bold face values represent
the highest accuracy result for a particular database
among all reduction rates evaluated.
Again, there is a tendency in which the method
achieves greater accuracy results with smaller reduc-
ICEIS 2008 - International Conference on Enterprise Information Systems
464

Table 6: Random Sampling predictive accuracy comparison (1/2).
Datasets Inst,Attrib, 1% 3% 5%
Classes k acc(%) T(s) red(%) k acc(%) T(s) red(%) k acc(%) T(s) red(%)
Adult 30162,14,2 277 82.88 81.2 98.96 176 82.93 231.9 97.04 120 83.11 397.6 94.92
Chess 3196,36,2 1 96.62 1.3 98.85 1 96.62 3.6 96.82 1 96.62 5.8 94.88
German 1000,20,2 1 72.10 0.2 97.37 5 73.22 0.3 96.05 7 73.27 0.5 93.42
Hdigit 10992,16,10 2 99.28 11.7 98.86 2 99.28 31.2 96.96 2 99.28 51.3 95.01
Hypo 3163,25,2 1 97.39 1.4 98.55 1 97.39 3.7 96.17 1 97.39 5.2 94.62
Isegm 2310,19,7 1 97.45 1.1 97.20 1 97.45 1.8 95.42 25 93.72 2.6 93.38
Landsat 6435,36,6 2 90.05 8.9 98.47 10 90.24 20.5 96.47 1 90.35 32.1 94.47
LetterR 20000,16,26 14 94.22 36.8 98.95 6 95.17 105.6 96.99 1 95.98 177.1 94.96
Mushr 8124,22,2 1 100 5.2 98.92 1 100 14.4 97.00 1 100 24.7 94.85
Nurse 12960,8,5 1 97.99 6.2 98.99 1 97.99 18.4 97.01 1 97.99 29.1 95.27
Sflare 1066,12,6 1 72.23 0.1 98.08 1 72.23 0.2 96.15 2 72.70 0.3 94.23
Shuttle 5800,9,6 1 99.66 2.7 98.55 1 99.66 6.3 96.61 1 99.66 9.9 94.67
Sick 3772,29,2 1 96.23 2.1 98.65 1 96.23 5.2 96.66 4 96.23 8.0 94.86
Splice 3190,61,3 581 93.67 2.1 98.89 581 93.67 5.8 96.92 581 93.67 9.5 94.96
Wavef 5000,40,3 25 84.08 6.6 97.97 212 84.84 12.8 96.06 253 85.12 19.0 94.15
Yeast 1484,8,10 1 52.11 0.3 96.59 1 52.11 0.4 95.45 26 58.70 0.6 93.18
Average 89.12 10.5 98.37 89.31 28.9 96.49 89.61 48.3 94.49
Table 7: Random Sampling predictive accuracy comparison (2/2).
Datasets Inst,Attrib, 10% 15% 20%
Classes k acc(%) T(s) red(%) k acc(%) T(s) red(%) k acc(%) T(s) red(%)
Adult 30162,14,2 98 83.08 771.6 90.14 121 83.11 1184.8 84.86 121 83.11 1552.6 80.16
Chess 3196,36,2 2 96.69 11.5 89.84 2 96.69 17.6 84.45 2 96.69 22.6 80.04
German 1000,20,2 7 73.27 0.9 88.16 9 74.08 1.2 84.21 9 74.08 1.6 78.95
Hdigit 10992,16,10 1 99.35 106.1 89.67 1 99.35 152.8 85.13 1 99.35 200.0 80.53
Hypo 3163,25,2 1 97.39 9.8 89.87 1 97.39 14.6 84.90 1 97.39 19.7 79.63
Isegm 2310,19,7 3 96.19 4.5 88.55 3 96.19 6.4 83.72 1 97.45 8.2 79.13
Landsat 6435,36,6 6 90.54 60.2 89.63 6 90.54 91.9 84.17 6 90.54 118.7 79.55
LetterR 20000,16,26 1 95.98 358.8 89.79 1 95.98 524.3 85.08 1 95.98 697.6 80.15
Mushr 8124,22,2 1 100 48.4 89.90 1 100 72.8 84.81 1 100 94.5 80.28
Nurse 12960,8,5 1 97.99 57.9 90.59 1 97.99 86.2 85.98 1 97.99 114.9 81.32
Sflare 1066,12,6 2 72.70 0.5 90.38 2 72.70 0.8 84.62 3 72.98 1.0 80.77
Shuttle 5800,9,6 1 99.66 18.8 89.89 1 99.66 27.7 85.10 1 99.66 36.3 80.47
Sick 3772,29,2 4 96.23 15.7 89.91 1 96.23 23.5 84.90 1 96.23 30.5 80.40
Splice 3190,61,3 581 93.67 18.6 90.14 581 93.67 28.3 84.99 581 93.67 36.6 80.59
Wavef 5000,40,3 336 85.16 34.0 89.53 248 85.20 49.9 84.64 142 85.08 64.1 80.26
Yeast 1484,8,10 28 58.65 1.0 88.64 8 58.51 1.4 84.09 49 58.27 1.8 79.55
Average 89.78 94.9 89.66 89.83 142.8 84.73 89.90 187.5 80.11
tion rates. As can be observed from Table 6 and Ta-
ble 7, the best average accuracy result (89.90%) oc-
curs with a value of k estimated from a reduction to
20%. Nevertheless, even for the value of k estimated
from a reduction to 1%, the average accuracy result
(89.12%) is better than any of the average accuracy
results obtained by other methods. The other meth-
ods performance is reported on Table 5.
The experimental results presented on Tables 6
and 7 show that sampling reduction allows the ex-
haustive approach to be performed in feasible com-
putational time with no significant loss of accuracy.
For example, the exhaustive approach performed on
the largest database (Adult) took 7826.0 seconds to
determine a value of k that achieves a 83.15% ac-
curacy. When a reduction to 1% was employed, a
value of k that achieves the accuracy of 82.88% was
estimated in 81.2 seconds. Considering the second
largest database (LetterR), the exhaustive approach
took 3514.0 seconds to determine a value of k that
achieves a 95.98% accuracy. When a reduction to 5%
was employed, the same value of k (therefore achiev-
ing the same accuracy result) was estimated in 177.1
seconds.
The reduction rates on computational time
achieved by sampling reduction were very homoge-
neous among the different databases. Besides, the re-
ductions on computational time were proportional to
the reductions on the databases. For example, when
the databases were reduced to 20%, an average reduc-
tion rate of 80.11% was achieved on computational
time.
5 CONCLUSIONS
This work presented methods capable of estimating
an adequate value for parameter k to be used with
the k-NN method. The proposed estimation processes
are preprocessing methods that perform a sampling
procedure over the original databases and, using the
generated set of sample, seek the most suitable value
for k.
Experimental results have shown that the estima-
tion of an adequate value for parameter k enhances
the k-NN method, allowing it to achieve greater accu-
racy results. Compared to other well-known methods,
such as decision trees and naive Bayes classification,
the k-NN became even more competitive.
Initially, an exhaustive evaluation of all possible
K-NN: ESTIMATING AN ADEQUATE VALUE FOR PARAMETER K
465

values of k was performed. The exhaustive approach
leads k-NN to achieve greater accuracy results. Nev-
ertheless, this evaluation is not tractable for large
databases.
In order to make the exhaustive approach feasible
when performed over large databases, a clustering-
based sampling of instances was analysed. Though
presenting good accuracy results, this technique did
not completely solved the problem of the high com-
putational time needed for the estimation of parame-
ter k.
Aiming at an even greater reduction on computa-
tional time, a second sampling strategy was analysed.
The random sampling led to an estimation of k in fea-
sible computational time. Its average accuracy result
for a reduction to 1% outperformed the average accu-
racy results of other strategies analysed.
REFERENCES
Aha, D. W. (1992). Tolerating noisy, irrelevant and novel
attributes in instance-based learning algorithms. Inter-
national Journal of Man-Machine Studies, 36(2):267–
287.
Angiulli, F. (2005). Fast condensed nearest neighbour rule.
In Proceedings of the 22
nd
International Conference
on Machine Learning, pages 25–32, Bonn, Germany.
Borsato, B., Merschmann, L., and Plastino, A. (2006). Em-
pregando a t´ecnica de agrupamento na estimativa de
um valor de k para o m´etodo k-nn. In Anais do II
Workshop em Algoritmos e Aplicac¸˜oes de Minerac¸˜ao
de Dados, realizado em conjunto com o XXI Simp´osio
Brasileiro de Banco de Dados, pages 33–40.
Duda, R. and Hart, P. (1973). Pattern Classification and
Scene Analysis. John Wiley & Sons, New York.
Duda, R., Hart, P., and Stork, D. (2000). Pattern Classifica-
tion. John Wiley & Sons.
Fix, E. and Hodges, J. L. (1951). Discriminatory analy-
sis, non-parametric discrimination: Consistency prop-
erties. Technical Report 21-49-004(4), USAF School
of Aviation Medicine, Randolph Field, Texas.
Guo, G., Wang, H., Bell, D., Bi, Y., and Greer, K. (2003).
kNN model-based approach in classification. In
Proceedings of CoopIS/DOA/ODBASE (LNCS 2888),
pages 986–996.
Han, J. and Kamber, M. (2005). Data Mining: Concepts
and Techniques. Morgan Kaufmann.
Haykin, S. (1994). Neural Networks: A Comprehensive
Foundation. Macmillan Publishing Company, New
York.
Heckerman, D. (1997). Bayesian networks for data mining.
Data Mining and Knowledge Discovery, 1(1):79–119.
Johns, M. V. (1961). Studies in Item Analysis and Predic-
tion. Stanford University Press, Palo Alto, CA.
Kaufman, L. and Rousseeuw, P. J. (1990). Finding Groups
in Data: An Introduction to Cluster Analysis. Wiley-
Interscience.
MacQueen, J. (1967). Some methods for classification and
analysis of multivariate observations. In Proceedings
of the 5
th
Symposium on Mathemtical Statistics and
Probability, volume 1, pages 281–297.
Newman, D. J., Hettich, S., Blake, C. L., and Merz, C. J.
(1998). UCI repository of machine learning databases.
Quinlan, J. R. (1986). Induction of decision trees. Machine
Learning, 1(1):81–106.
Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-
ing. Morgan Kaufmann.
Vapnik, V. N. (1995). The Nature of Statistical Learning
Theory. Springer-Verlag, New York.
Wang, H. (2003). Nearest neighbours without k: A clas-
sification formalism based on probability. Technical
Report CS-03-02, Faculty of Informatics, University
of Ulster, N.Ireland, UK.
Wettschereck, D. and Dietterich, T. G. (1994). Locally
adaptive nearest neighbor algorithms. In Cowan, J.D.,
Tesauro, G., and Alspector, J., editors, Advances in
Neural Information Processing Systems, volume 6,
pages 184–191. Morgan Kaufmann, San Mateo, CA.
Witten, I. H. and Frank, E. (2005). Data Mining: Practi-
cal Machine Learning Tools and Techniques. Morgan
Kaufmann, second edition.
ICEIS 2008 - International Conference on Enterprise Information Systems
466
