
DATA ENCRYPTION AND DECRYPTION USING ANZL
ALGORITHM
Artan Luma and Nderim Zeqiri
CST, SEE University, Ilindenska bb, Tetovo, Macedonia
Keywords: Cryptography, Algorithm, Security, ANZL.
Abstract: What is the ANZL Algorithm? It is a genuine result of our work which is theoretically and practically
proved. By using the ANZL Algorithm, we can test whether a given number x belongs to Lucas’s series. It
can also be used to find a sequence of Lucas’s numbers, starting from any number x. If a given number x,
completes the relation 5·x
4λ
, we can say that it is a Lucas number and we mark it as L
x. From
the pair of numbers
L
,λ
, we can find the preceding L
and the succeeding L
e L
. Based on these
three elements of Lucas’s series, we can create the key for data encryption and decryption.
1 ALGORITHM ANZL
Based on Fibonacci series:
1, 1, 2, 3, 5, 8, 13, 21, 34, … (1)
We will be able to get the elements of Lucas’s series
using:
L
F
F
·
F
(2)
Where n, m N and m1,n2·m. If m, is
even, we use , if m, is odd, the we use . For
m1 and n3, we have:
L
F
F
F
1 (3)
For m2 and n5, we have:
L
F
F
F
3 (4)
For m3 and n7, we have:
L
F
F
F
4 (5)
For m4 and n9, we have:
L
F
F
F
7 (6)
For m5 and n11, we have:
L
F
F
F
11 (7)
Based on this general formula, using Fibonacci’s
numbers we will generate Lucas’s series of numbers:
1, 3, 4, 7, 11, 18, 29, … (8)
Theorem 1: For Lucas’s seires L
,nN, we have:
L
L
L
, n 1 (9)
Theorem 2: For odd members of Lucas’s series
L
, n N, we have:
L
·
·L
·
L
·
5 (10)
Theorem 3: For even members of Lucas’s series
L
,nN, we have:
L
·
·L
·
L
·
5 (11)
With the help of Theorems 2 and 3 we can find the
algorithm to test if a number belongs to Lucas’s
series or not.
L
·
·L
·
L
·
5 (12)
From Theorem 1, L
·
, we can write:
L
·
L
·
L
·
(13)
As a result:
L
·
L
·
L
·
(14)
If:
L
·
L
·
L
·
2·L
·
·L
·
L
·
(15)
L
·
L
·
L
·
2·L
·
·L
·
L
·
(16)
Now, the expression
L
·
L
·
, can be
written as:
L
·
L
·
L
·
L
·
4·L
·
·L
·
(17)
220
Luma A. and Zeqiri N. (2008).
DATA ENCRYPTION AND DECRYPTION USING ANZL ALGORITHM.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - ISAS, pages 220-223
DOI: 10.5220/0001688102200223
Copyright
c
SciTePress

So that we have:
(18)
From Theorem :
(19)
(20)
(21)
Ω
(22)
Ω is the sum of adjacent members of
, of
Lucas’s series. We can prove in the same way that:
Ψ
(23)
Ψ is the sum of adjacent members of
. Based
on the above-mentioned relations, we can test
wthether a given number belongs to Lucas’s
series. We can also use this to find a sequence of
Lucas’s numbers starting from any number . If ,
completes the relation
, we cab say
that it is Lucas’s number and we mark it as
.
From the pair
, we can also find the
preceeding and succeeding numbers
and
of
.
(24)
Since we have found
, we can find
the whole series of Lucas’s numbers:
(25)
Table 1.
x
λ
1 5 2 1 3
2 0 -1 2 1
3 5 1 3 4
4 10 3 4 7
7 15 4 7 11
11 25 7 11 18
18 40 11 18 29
29 65 18 29 47
We will now see how we can encrypt or decrypt a
message by using the ANZL algorithm to create the
key. Let be the message (plaintext), and the key.
is the encrypted message (ciphertext). If we want
to encrypt a message, we will use this formula:
(26)
If we want to decrypt a text, we will use:
(27)
We will now show how to create the key. First of all,
we choose a number and this number is put in the
ANZL algorithm to test whehter it belongs to
Lucas’s series or not. The formula of the ANZL
algorithm which tests the number is:
(28)
If , meets this condition, then
, which means
that is a number in the Lucas’s series. Since
and , we can easily find
and
. These two
elements of Lucas’s series are found by using the
formulas:
(29)
Now that we have found Lucas’s elements
, we can construct the whole series if Lucas’s
numbers:
(30)
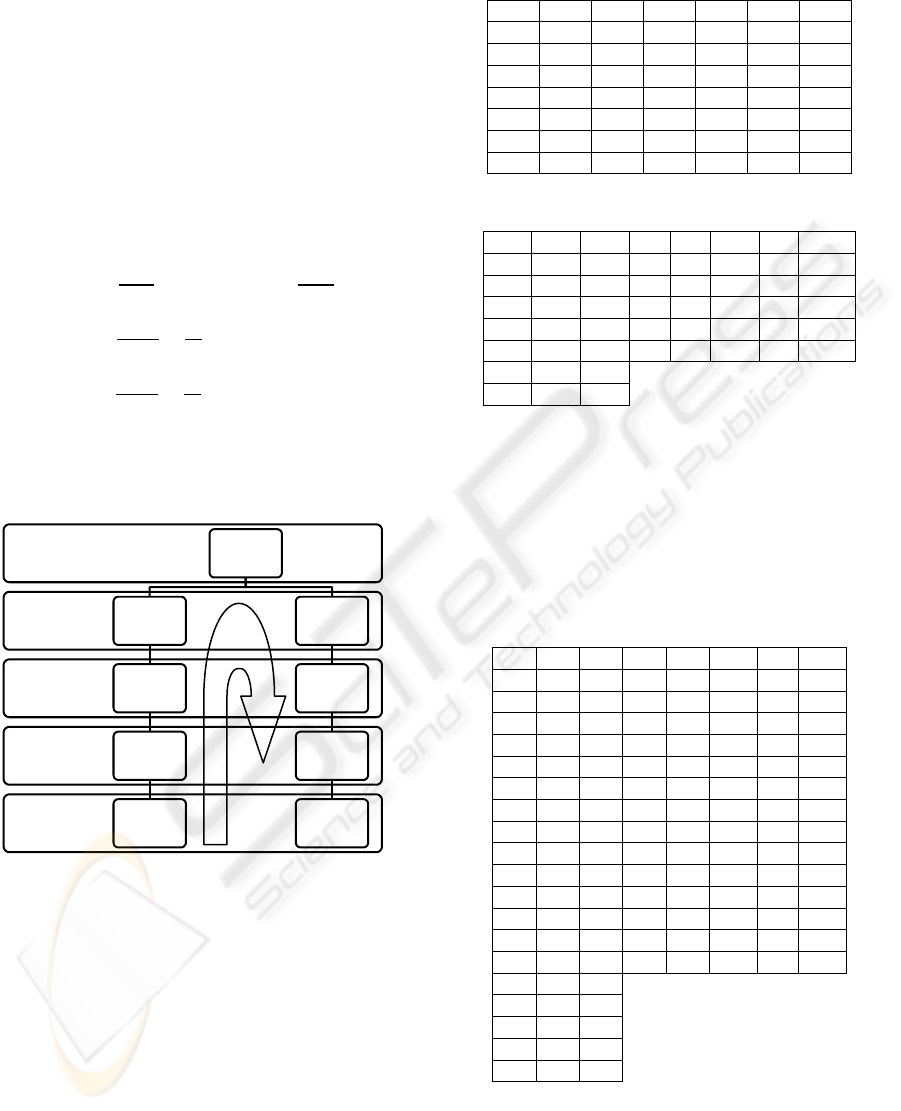
We will now design a scheme to create the key. In
order to do this, the most important are the levels.
Figure 1.
If we want to create a key with level , then its keys
will be:
(31)
This means that the key will consist of five
elements. The number of elements is determined by
this formula:
(32)
, is the number of elements of the key and are
the levels. Let’s have a plaintext now: South East
Level n
Level 3
Level 2
Level 1
Level 0 Ln
Ln‐1
Ln‐2
Ln‐3
...
Ln+1
Ln+2
Ln+3
...
DATA ENCRYPTION AND DECRYPTION USING ANZL ALGORITHM
221
European University which we want to encrypt. First
of all we have to have , so that it meets the
condition of the ANZL algorithm:
(33)
For we will get:
(34)
This means that the condition of the ANZL
algorithm has been met so that we have
and
. Knowing the pair
, we will
find the preceeding and succeeding numbers of
:
(35)
(36)
(37)
After we have found these three elements of Lucas’s
series:
, we will design the scheme of
creating the key.
Figure 2.
If we decide to create a Level që do të thotë
, we get:
(38)
This means that the key will consist of five
elements:
(39)
The text is now being converted into numbers. In
order to do this we use the Table 1:
We get the text: South East European University and
we convert it into numbers.
Table 2.
a b c d e f g
0 1 2 3 4 5 6
h i j k l m n
7 8 9 10 11 12 13
o p q r s t u
14 15 16 17 18 19 20
v w x y z
21 22 23 24 25
Table 3.
s o u t h e a s
18 14 20 19 7 4 0 18
t e u r o p e a
19 4 20 17 14 15 4 0
n u n i v e r s
13 20 13 8 21 4 17 18
i t y
8 19 24
In order to encrypt the message, we use:
(40)
The key is:
(41)
We take the key and we put it into the message
which we want to encrypt:
Table 4.
s o u t h e a s
18 14 20 19 7 4 0 18
4 7 11 18 29 4 7 11
22 21 5 11 10 8 7 3
W V F L K I H D
t e u r o p e a
19 4 20 17 14 15 4 0
18 29 4 7 11 18 29 4
11 7 24 24 25 7 7 4
L H Y Y Z H H E
n u n i v e r s
13 20 13 8 21 4 17 18
7 11 18 29 4 7 11 18
20 5 5 11 25 11 2 10
U F F L Z L C K
i t y
8 19 24
29 4 7
11 23 5
L X F
If want to send this encrypted message to anyone,
apart from the message itself, we also need to send
the pair of numbers
. The person
receiving the message can decrypt it by finding first
Level n
Level 3
Level 2
Level 1
Level 0 11
7
4
3
...
18
29
47
...
ICEIS 2008 - International Conference on Enterprise Information Systems
222

and then the key. Based on the ANZL algorithm,
we find the values of :
(42)
For , we get:
(43)
. Knowing
, we will find
the preceeding and the succeeding numbers
:
(44)
(45)
(46)
Figure 3.
Table 5.
W V F L K I H D
22 21 5 11 10 8 7 3
4 7 11 18 29 4 7 11
18 14 20 19 7 4 0 18
s o u t h e a s
L H Y Y Z H H E
11 7 24 24 25 7 7 4
18 29 4 7 11 18 29 4
19 4 20 17 14 15 4 0
t e u r o p e a
U F F L Z L C K
20 5 5 11 25 11 2 10
7 11 18 29 4 7 11 18
13 20 13 8 21 4 17 18
n u n i v e r s
L X F
11 23 5
29 4 7
8 19 24
i t y
After having found these three elements of Lucas’s
series:
, we will design the scheme
for creating the key.
We know that Level of key is which means
, so that:
(47)
This means thta the key will consist of five elements
of Lucas’s series:
(48)
Having the key, is quite easy to encrypt the text by
using:
(49)
2 CONCLUSIONS
The aim of the ANZL Algorithm is to test whether a
number belongs to Lucas’s series or not. If it does,
then it is very easy to find the preceeding and
succeeding numbers
.This algorithm
can also be used for purposes of data encryption and
decryption in terms of creating the keys.
REFERENCES
Introduction to cryptography: with coding theory by Wade
Trappe; Lawrence C Washington, Publisher: Upper
Saddle River, N.J.: Pearson Prentice Hall, ©2006,
ISBN: 0131862391
Applied Cryptography: Protocols, Algorithms, and Source
Code in C, Second Edition (Paperback) by Bruce
Schneier; Paperback: 758 pages; Publisher: Wiley;
2nd edition (October 18, 1996); Language: English;
ISBN-10: 0471117099; ISBN-13: 978-0471117094
Modern Cryptography: Theory and Practice
(Hardcover)by Wenbo Mao; Hardcover: 740 pages;
Publisher: Prentice Hall PTR; 1st edition (July 25,
2003); Language: English; ISBN-10: 0130669431;
ISBN-13: 978-0130669438
Practical Cryptography (Hardcover) by Niels Ferguson,
Bruce Schneier; Hardcover: 432 pages Publisher:
Wiley (April 17, 2003); Language: English; ISBN-10:
047122894X; ISBN-13: 978-0471228943
Schneier's Cryptography Classics Library: Applied
Cryptography, Secrets and Lies, and Practical
Cryptography (Paperback) by Bruce Schneier;
Paperback: 1664 pages; Publisher: Wiley (October 22,
2007); Language: English; ISBN-10: 0470226269;
ISBN-13: 978-0470226261.
Level n
Level 3
Level 2
Level 1
Level 0 11
7
4
3
...
18
29
47
...
DATA ENCRYPTION AND DECRYPTION USING ANZL ALGORITHM
223
