
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR
RECOMMENDATION MAKING
Li-Tung Weng, Yue Xu, Yuefeng Li and Richi Nayak
Faculty of Information Technology, Queensland University of Technology, 4001 Queensland, Australia
Keywords: Recommender System, Neighbourhood Formation, Taxonomic Information.
Abstract: Recommender systems produce personalized product recommendations during a live customer interaction,
and they have achieved widespread success in e-commerce nowadays. For many recommender systems,
especially the collaborative filtering based ones, neighbourhood formation is an essential algorithm
component. Because in order for collaborative-filtering based recommender to make a recommendation, it is
required to form a set of users sharing similar interests to the target user. “Best-k-neighbours” is a popular
neighbourhood formation technique commonly used by recommender systems, however as tremendous
growth of customers and products in recent years, the computation efficiency become one of the key
challenges for recommender systems. Forming neighbourhood by going through all neighbours in the
dataset is not desirable for large datasets containing million items and users. In this paper, we presented a
novel neighbourhood estimation method which is both memory and computation efficient. Moreover, the
proposed technique also leverages the common “fixed-n-neighbours” problem for standard “best-k-
neighbours” techniques, therefore allows better recommendation quality for recommenders. We combined
the proposed technique with a taxonomy-driven product recommender, and in our experiment, both time
efficiency and recommendation quality of the recommender are improved.
1 INTRODUCTION
Recommender systems are designed to benefit
humans’ information extracting experiences by
giving information recommendations according to
their information needs. User based collaborative
filtering is the most fundamental and widely applied
recommendation technique(Schafer et al., 2000), it
generates recommendations based on finding items
that are commonly preferred by the neighbourhoods
of the target users. Specifically, a target user’s
neighbourhood is a set of users sharing similar
preferences to the target user(Awerbuch et al.,
2005). Neighbourhood formation in collaborative
filtering techniques requires comparing the target
users’ preferences to the preferences of all users in
the dataset, and such preference comparison process
can become a major computation efficiency
bottleneck for recommenders. For large datasets,
neighbourhood formation process requires a large
amount of I/O to retrieve user profiles, and each user
profile may be represented by a very high dimension
vector, hence the similarity computation between the
vectors can be very expensive.
Our main contribution in this paper is a novel
neighbourhood estimation method called “relative
distance filtering” (RDF), it is based on pre-
computing a small set of relative distances between
users, and using the pre-computed distances to
eliminate most unnecessary similarity comparisons
between users. The proposed RDF method is also
capable of dynamic handling frequent data update;
whenever the user preferences in the dataset are
added, deleted or modified, the pre-computed
structure cache can also be efficiently updated.
Part of our research is to develop a novel
collaborative filtering based recommender that
utilizes the item taxonomy information for its user
preference representation. Our work is based on a
well-known taxonomy recommender, namely
taxonomy product recommender (TPR), proposed by
Ziegler (Ziegler et al., 2004) which utilizes the
taxonomy information of the products to solve the
data sparsity and cold-start problems. TPR
outperforms standard collaborative filtering systems
with respect to the recommendation accuracy when
producing recommendations for sites with data
sparsity. However, the time efficiency of TPR drops
12
Weng L., Xu Y., Li Y. and Nayak R. (2008).
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR RECOMMENDATION MAKING.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - SAIC, pages 12-19
DOI: 10.5220/0001695000120019
Copyright
c
SciTePress

significantly when dealing with huge number of
users, because the user preferences in TPR are
represented by high dimensional vectors. We
applied the proposed RDF technique to the TPR and
the experiment results show that by utilizing the
proposed technique, both the accuracy and
efficiency of TPR are significantly improved.
2 RELATED WORK
Neighbourhood formation is a process required by
most collaborative filtering based recommenders to
find users with similar interests to the target user.
Sarwar (Sarwar et al., 2002) proposed an efficient
neighbourhood selection method by pre-computing
users into clusters. However, clustering is an
expensive process and can only be done offline.
Datasets keep changing over time. Therefore the
overall quality of the result neighbourhood based on
existing clusters will degrade until the next
clustering update. Moreover, clustering based
neighbourhood selection favours target users nearby
cluster centres, and for other users located at
surrounding cluster edges the quality of their result
neighbourhoods are usually poor because their
actual neighbours are very likely in other clusters
(Sarwar et al., 2002). There are also several
neighbourhood formation algorithms developed
specifically for high dimensional data, such as
RTree (Manolopoulos et al., 2005), kd-Tree
(Bentley, 1990), etc. The basic idea behind these
algorithms is to index these high dimensional data
into a search tree structure, and within each level,
the children nodes subdivides the cluster their parent
node holds into finer clusters and each tree node
holds one of the cluster spaces. The search
efficiency of these algorithms is very impressive,
because the search space are quadratically reduced
in each tree level (i.e. O(logN)). However, they
suffer from similar problems to cluster based
neighbourhood search, which is “loss of precision”.
In fact, these algorithms usually produce worse
result than clustering based method. Moreover,
because the internal tree structures for indexing the
data are fairly complex, therefore these algorithms
are usually memory intensive and slow in
initialization. The proposed RDF technique is not as
good as these tree-structure based methods in terms
of computation efficiency, however it is still more
efficient than cluster based search method. In terms
of accuracy, the proposed method produces much
better result than these tree-structure based methods
because it does not constrain neighbourhood search
within local clusters. The internal structure of the
proposed RDF technique can be updated
dynamically in real time and requires only very
small amount of physical memory.
3 TAXONOMY PRODUCT
RECOMMENDER
An overview of taxonomy-driven product
recommender (TPR) proposed by Ziegler (Ziegler et
al., 2005, Ziegler et al., 2004) is given in this
section.
3.1 Item Taxonomy Model
We envision a world with a finite set of users
,
,…,
and a finite set of items
,
,…,
. For each user
, he or she
is associated with a set of corresponding implicit
ratings
, where
. Unlike explicit ratings in
which users are asked to supply their perceptions to
items explicitly in a numeric scale, implicit ratings
such as transaction histories, browsing histories, etc.,
are more common and obtainable for e-commerce
sites and communities.
In standard collaborative filtering
recommenders, user profiles are represented by -
dimensional vectors, where || and each
dimension represents an explicit item rating.
However, for many systems, can be very large
and the number of ratings made by each user can be
very small. This problem is often addressed as cold
start problem or data sparsity problem.
Data sparsity problem is relieved with TPR,
because instead of using the product-rating vectors
with || dimensionalities as user profiles, TPR uses
taxonomy vectors with dimensionalities, where
is the number of topics in the product taxonomy
space. Specifically, we denote the taxonomy vector
for
as v
v
,v
,…,v
, and each dimension of
v
indicates the degree of
’s interest to the
corresponding topic. The taxonomy vector in TPR
has three advantages over standard product rating
vector. Firstly, for most e-commerce sites is much
smaller than ||, and therefore it can yield better
computational performances. Secondly, because the
taxonomy vector records the user taxonomy
preferences instead of item preference, and different
items can share their descriptors entirely or partially,
thus, even for users with no common item interests,
their profiles can still be correlated. Thirdly, the
construction of the taxonomy vector can be done
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR RECOMMENDATION MAKING
13

with only implicit ratings, and therefore it
effectively solved the data sparsity problem.
3.2 Recommendation Generation
In this paper, the distances between user taxonomy
vectors are computed by Euclidean distance,
specifically:
,
∑
|
|
(1)
Based on the distance measure, target user u
‘s
neighbourhood cliqueu
can be formed by
selecting n users from u
U\u
with shortest
distances to u
. By extracting the items implicitly
rated by the neighbourhood, a candidate item list is
formed for u
’s personalized recommendation list,
formally:
|
\
(2)
The items in the candidate list B
need to be
ranked according to their closeness to the target
user’s personal interest. The ranking equation to
weight u
’s possible interest towards t
’s shown
below:
1
,
∑
,
|
|
(3)
,where A
t
u
cliqueu
|t
R
.
In equation (3), the computed score is negated
because the proximity measure is distance based (i.e.
small value indicates strong similarity), thus, by
negating the result score we allow larger weight
values of w
t
indicating higher item interests.
ut
creates a dummy user for item t
, so the
proximity of the taxonomy vectors between u
and
t
can be measured. The conversion process simply
creates a user u
with R
t
.
Finally, after the candidate item weights are
computed, the top m items with highest weight
values are recommended to the target user.
4 PROPOSED APPROACH
In this paper, we identified two aspects in TPR that
can be improved.
Firstly, even though the product rating vectors
are compressed into taxonomy vectors with smaller
numbers of dimensionalities, however, for datasets
with a large amount of users and extensive
taxonomy structures, the neighbourhood formation
will become one of the computation efficiency
bottlenecks in TPR, because it requires an extensive
amount of I/O to retrieve user profiles (i.e.
taxonomy vectors) from the database, and the
proximity computation (i.e. equation (1)) for high
dimensional vectors is expensive as well.
Next, in Ziegler’s TPR implementation (Ziegler
et al., 2004), the “best-n-neighbours” is applied as
the neighbourhood selection method since “best-n-
neighbours” performs better than “correlation-
threshold” for sparse dataset (Ziegler et al., 2004).
However, because the value of is pre-specified in
“best-n-neighbours”, it means that the resulting
neighbourhoods will be biased for users with true
neighbours of less than (Li et al., 2003). This issue
is particularly sensible for users with unusual tastes,
as it is likely that a portion of their neighbourhoods
formed by “best-n-neighbours” might contain
neighbours that are dissimilar to them. For example,
if a user has distinct tastes, then he or she might only
share similar tastes with only 2 other users, the
recommendation result for this user might be biased
if a neighbourhood with 20 users are used.
In this paper, we propose a novel neighbourhood
estimation method which is both memory and
computation efficient. By substituting the proposed
technique with the standard “best-n-neighbours” in
TPR, the following two improvements are achieved:
z The computation efficiency of TPR is greatly
improved.
z The recommendation quality of TPR is also
improved as the impact of the “fixed
neighbours” problem has been reduced. That is,
the proposed technique can help TPR locate the
true neighbours for a given target user (the
number of true neighbours might be smaller than
), therefore the recommendation quality can be
improved as only these truly closed neighbours
of the target user can be included into the
computation.
4.1 Relative Distance Filtering
Forming neighbourhood for a given user
with standard “best-n-neighbours” technique
involves computing the distances between
and all
other users and selecting the top neighbours with
shortest distances to
. However, unless the
distances between all users can be pre-computed
offline or the number of users in the dataset is small,
forming neighbourhood dynamically can be an
expensive operation.
Clearly, for the standard neighbourhood
formation technique described above, there is a
significant amount of overhead in computing
distances for users that are obviously far away (i.e.,
dissimilar users). The performance of the
ICEIS 2008 - International Conference on Enterprise Information Systems
14

neighbo
u
improve
d
dissimil
a
comput
a
exclusio
n
simple
g
very cl
o
distance
s
space sh
In F
i
dimensi
o
dot on t
h
and the
d
neighbo
u
randoml
y
set, and
comput
e
users).
Bas
e
to obse
r
distance
s
forming
comput
e
whi
c
whe
r
,
In e
q
distance
s
Modus
t
of an i
m
implicat
i
implicat
i
then
a
distance
user
neighbo
u
u
rhood for
m
d
if we e
x
a
r users f
r
a
tion. In the
n
or filterin
g
g
eometrical i
o
se to each
s
to a given
r
ould be simil
a
i
gure 1, a use
r
o
nal plane w
h
h
e plane. In
t
d
ots embrace
d
u
rs of
.
y
selec
t
ing a
then
’s d
i
e
d and sorte
d
Figure 1: P
r
e
d on the tria
n
r
ve that all
s
to
. T
h
’s neigh
b
e
distances b
e
c
h is defined
a
r
e
is an
,
.
q
uation (4),
|
s
fro
m
to
t
olens infere
n
m
plication is
i
on must be
i
on men
t
ion
e
a
nd
are n
o
threshold. I
f
can
be
u
rhood. If
m
ation can
x
clude most
r
om the
d
proposed R
D
g
process is
mplication: i
other in a
s
r
andomly sel
e
a
r.
r
set is proj
h
ere each use
t
he figure,
d
by small cir
c
The RDF
m
reference u
s
i
stances to a
l
(
and
a
r
ojected user p
r
n
gle inequalit
y
’s neighb
o
h
is means, i
n
b
ourhood,
w
e
tween
an
d
a
s:
,
|
abbreviate
d
|
is the
and
to
n
ce rule, i.e.,
false, the
a
false, from
e
d above, if
|
o
t close to e
f
|
|
is l
e
excluded
is set to a
be drasti
c
of these
v
d
etailed dist
a
D
F method,
achieved wi
t
f two points
s
pace, then
t
e
cted point i
n
ected onto a
t
r is depicted
is the target
u
c
les are the to
p
m
ethod starts
s
e
r
in the
l
l other user
s
a
re also refer
e
r
ofiles.
y
theme, it is
o
urs have si
m
n
the proces
s
w
e only nee
d
d
the users i
n
|
d
denotation
difference o
f
. Accordi
n
if the conse
q
a
ntecedent o
f
the geomet
r
|
is l
a
ach other.
arger than
,
from the
larger value,
c
ally
v
ery
a
nce
this
t
h a
are
t
heir
n
the
t
wo-
as a
u
ser,
p
15
by
user
s
are
e
nce
easy
m
ilar
s
of
d
to
n
se
t
4
for
f
the
n
g to
q
uent
f
the
r
ical
a
rge,
is a
,
the
’s
the
dis
t
inc
l
p
er
f
wil
l
In
o
dis
t
nei
g
est
i
ex
a
obt
a
)
fin
a
red
u
(i.e
tha
t
tha
n
‘s
int
e
‘
co
m
int
e
im
p
Fig
u
use
r
4.
2
Th
e
ord
est
i
b
e
a
ord
ref
e
b
e
c
the
lar
g
rad
i
sh
o
for
of
r
t
ance th
r
esho
l
l
uded in the
f
ormance wil
l
be included
o
ur experime
t
ance
b
etwee
n
g
hbour
To furthe
r
i
mation, we
c
a
mple
an
d
a
in more esti
m
)
. With multi
p
a
l estimated
u
ced by
.
t
, the intersec
t
n
the entire s
e
most close
e
rsection are
a
‘
s neighbour
h
m
putations o
n
e
rsected spa
c
p
roved.
u
re 2: Estimat
e
r
s.
2
Refere
n
e
reference us
e
er to optimiz
e
i
mated search
i
a
s small as p
o
er to achie
v
e
rence users
n
c
ause if the re
f
ring border
s
g
e overlap (si
n
i
uses). More
o
o
uld be kept s
m
all our expe
r
r
eference user
l
d is relaxed,
t
neighbourh
o
l be decreas
e
in the actual
d
nt, is set t
o
n
the referen
c
.
r
optimize
c
an select mo
r
d
) into the
m
ated search
i
p
le estimate
d
searching sp
a
intersecti
n
). It can be
t
ed searching
e
t, and most i
m
users. O
n
a
need to be
c
h
ood. The a
c
n
ly need to b
e
c
e, thus the
e
d searching s
p
n
ce User S
e
e
r selection i
s
e
the perfor
m
i
ng space (i.e
.
o
ssible for an
y
v
e it, the d
n
eed to be a
s
f
erence users
a
s
of their se
a
n
ce they all h
a
o
ver, the nu
m
m
all (we onl
y
r
iments), bec
a
s increases, t
h
t
hus more us
e
o
od. In this
e
d because
m
d
istance com
p
o
the one te
n
c
e user and it
the neig
h
r
e reference
u
estimation
p
i
ng spaces (i.
e
d
searching s
p
a
ce can be
d
n
g these
observed in
space is mu
c
m
portantly, it
n
ly the user
s
c
hecked for
d
c
tual I/O an
d
e
conducted
w
efficiency i
s
p
ace with thre
e
e
lection
s
important fo
r
m
ance of TPR
,
.
)
y
given targe
t
istances bet
w
s
far as poss
i
a
re close to e
a
a
rch spaces
w
a
ve similar c
e
m
ber of refere
n
y
use 3 refere
a
use when th
e
h
e time requir
e
e
rs can be
case, the
m
ore users
p
utations.
n
th of the
s furthest
h
borhood
u
sers (for
p
rocess to
e
.
and
p
aces, the
d
rastically
spaces
Figure 2
c
h smaller
covers
s
in the
d
etermine
d
distance
w
ithin the
s
greatly
e
reference
r
RDF. In
,
the final
)
needs to
t
users. In
w
een the
i
ble. It is
a
ch other,
w
ill result
e
ntres and
n
ce users
nce users
e
number
e
d for the
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR RECOMMENDATION MAKING
15
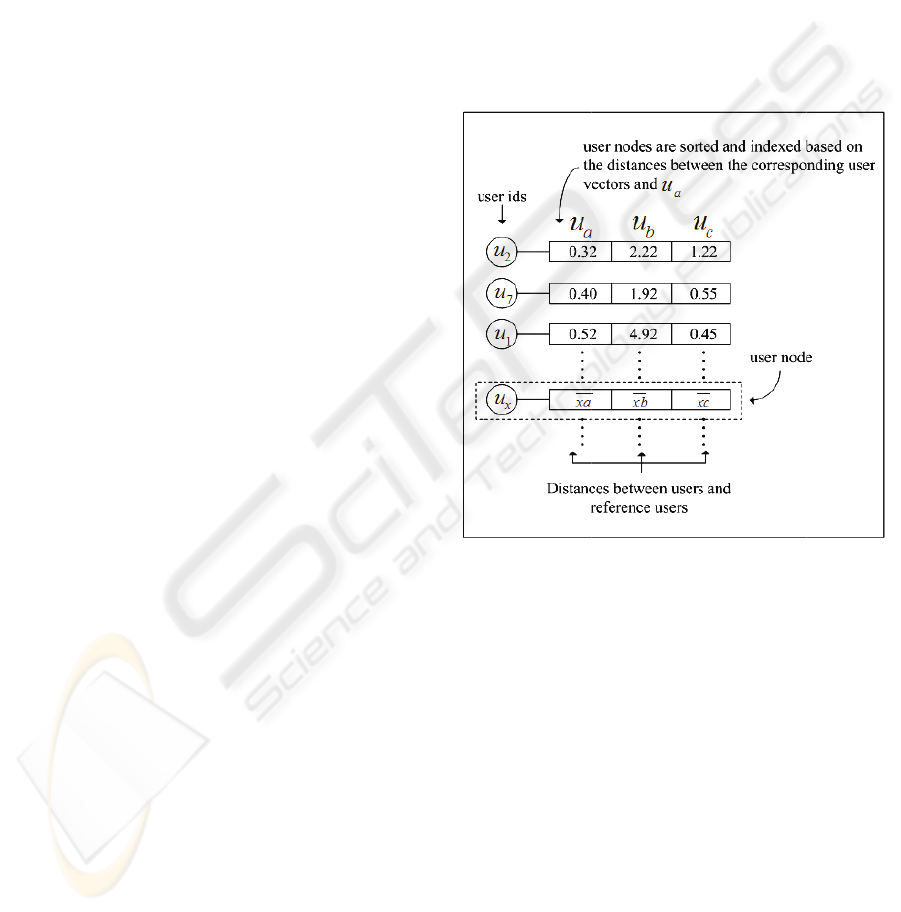
offline r
required
too.
In o
u
initializ
e
first ref
e
comput
e
with th
e
second
argmax
the furt
h
ar
g
and set
method,
kept si
m
users ar
e
4.3
P
This se
c
of the p
r
4.1 and
p
ower o
f
First
distance
s
meant
comput
a
expensi
v
distance
s
offline
i
cache, a
the me
m
recomm
e
searchin
g
formati
o
depicte
d
In t
h
with a
d
user
b
asicall
y
1.
U
s
p
r
o
m
e
st
o
id
e
th
e
2.
D
i
di
s
us
e
ve
th
r
th
e
is
eference use
r
for caching
u
r implemen
t
e
d with a si
m
e
rence user
e
its distance
s
e
computed
reference
h
est neighbo
u
g
max
as the t
h
it is ensured
t
m
ple and effi
c
e
also very di
s
P
roposed
R
c
tion describe
r
oposed RD
F
4.2. With th
e
f
RDF is max
i
of all, it i
s
s
between us
e
to be co
m
a
tion efficie
n
v
e than the o
n
s
are comp
u
i
nto a data s
t
nd the searc
h
m
ory in the i
n
e
ndation p
r
g
cache is
s
o
n processes
.
d
in Figure 3.
h
e searching
d
ata structur
e
,
denot
e
y
stores two t
y
s
er ID: Inst
e
o
files or th
e
e
mory, only
o
red in the c
a
e
ntify and ret
r
e
database.
i
stances to
s
tances from
e
r to the re
f
ctor. In our
i
r
ee referenc
e
e
refore the d
i
,
,
.
W
r
initializatio
n
the sorted d
i
t
ation, the re
m
ple two-
p
as
is chosen r
a
s
to all other
distances w
e
user
s
u
,
. Fina
u
r
for
a
,
h
ird referenc
e
t
hat the initia
l
c
ient, and th
e
s
tant from eac
h
R
DF Imple
m
s in detail th
F
method dis
c
e
proposed i
m
i
mized.
s
important
e
rs and refer
e
m
puted onli
n
n
cy of this
p
n
e by one sea
r
u
ted, structu
r
t
ructure calle
d
h
ing cache w
i
n
itialization s
t
r
ocess. Thi
s
s
hared by a
l
.
The detai
cache, each
u
e
called “use
r
e
s
’s user
n
y
pes of infor
m
e
ad of fittin
g
e
user taxon
o
the user id
i
a
che. The us
e
r
ieve the actu
the Refere
n
the user nod
e
f
erence users
i
mplementati
o
e
users
,
i
stance vecto
r
W
e denote the
n
and the me
m
i
stances inc
r
ference user
s
s technique.
a
ndomly, an
d
users in .
N
e
can obtain
u
ch that
lly, we again
a
nd
such
,
e
user. With
l
ization proc
e
e
result refer
e
h
other.
m
entation
e implement
a
c
ussed in sec
t
m
plementation
,
to note that
e
nce users ar
e
n
e, because
p
rocess is
m
r
ch. Instead, t
h
r
ed and ind
e
d
RDF searc
h
i
ll be loaded
t
age of the o
n
s
pre-comp
l
l neighbour
h
led structur
e
u
ser is assoc
i
r
node”. For
n
ode. A user
n
m
ation for a u
s
g
the entire
o
my vector
i
s required t
o
e
r ids are us
e
al user profil
e
n
ce Users:
e
’s correspon
are stored
i
o
n, we have
and
,
r
for user no
d
distance vect
o
m
ory
r
ease
s
are
The
d
we
N
ext,
the
find
that
,
this
e
ss is
e
nce
a
tion
t
ions
,
the
the
e
not
the
m
ore
h
ese
e
xed
h
ing
into
n
line
uted
h
ood
e
is
i
ated
any
n
ode
s
er:
user
into
o
be
e
d to
e
s in
The
ding
i
n a
only
and
d
e
o
r of
sea
r
b
in
a
use
r
are
use
r
Wi
t
ca
n
set
t
on
e
tre
e
eq
u
p
ro
co
m
me
m
b
e
c
co
m
dis
t
use
r
for
m
use
r
me
m
is
t
use
r
η
as
,
corr
e
respecti
v
In order to
r
ching space
a
ry tree stru
c
r
nodes. The
the distance
r
s, that is, the
t
h the three
d
n
be efficient
l
t
ings, that is,
t
e
of the three
i
Figure 3: Str
u
Because the
e
structure,
u
ation (4) i
s
||. Note,
cess is very
e
m
putation ca
n
m
ory (thus n
o
c
ause each i
n
m
parison of t
w
t
ances betwe
e
r
s are ne
e
m
ation proce
s
r
s are requir
e
m
ory require
m
t
rivial, beca
u
r
s.
,
,
w
h
e
sponds to
v
ely.
efficiently
r
as describe
c
ture is used
index keys u
s
between the
index keys f
o
d
ifferent inde
x
l
y sorted wi
t
t
he user node
i
ndex keys.
u
cture for the R
D
user nodes a
r
the compu
t
s
optimized
this estimate
e
fficien
t
, not
o
n
be done wit
h
o
database I/
O
n
dex key lo
o
w
o double v
a
e
n the target
u
e
de
d
during
s
s, the user pr
o
e
d to be sto
r
m
ent for the
r
u
se there are
h
ere
corre
s
and
corre
s
r
etrieve the
e
e
d in equati
o
to index an
d
s
ed for each
u
user and the
o
r
are
,
x
keys, the u
s
t
h different i
n
s can be sort
e
D
F searching
c
r
e stored in t
h
t
ation effici
e
to
d user space
o
nly because
t
h
in a small
a
O
is required),
o
kup involve
a
lues. Finally
,
u
sers and the
the neigh
b
o
files for the
r
ed in the c
a
r
eference use
only three
s
ponds to
s
ponds to
e
stimate
d
o
n (4), a
d
sort the
u
ser node
reference
and
.
s
er nodes
n
dex key
e
d by any
c
ache.
h
is binary
e
ncy for
, where
retrieval
t
he whole
a
mount of
it is also
s only a
,
because
reference
b
ourhood
reference
a
che. The
r profiles
reference
ICEIS 2008 - International Conference on Enterprise Information Systems
16

Given that the RDF searching cache is properly
initialized, the detailed RDF procedure is described
below:
RDF Algorithm
1) Let
be the target user, n be the pre-specified
number of neighbours for
.
2) Use the indexed tree structure to locate the
minimal user nodes set within the given
boundary:
|
,
where
,
,
which achieves
minimal search space. Note, the actual
implementation of
’s computation can be
very efficient. By utilizing the pre-computed
searching cache, the estimation of user nodes
size does not involve looping through the user
nodes one by one.
3) Based on step 2,
is the primary index key
used to sort and retrieve
, and it is one of
,
and
. The rest two index keys (also in
,
,
) are denoted as
and
.
4) We refine the searching space
by using
reference users
and
. This process is
similar to finding the intersected space
as described in section 4.2
FOR
DO
IF
or
or
or
THEN
remove
from
END IF
END FOR
5) Do the standard “best- n-neighbours” search
against the estimated searching space
, and
return the result neighbourhood for
.
5 EXPERIMENTS
This section presents empirical results obtained from
our experiment.
5.1 Experiment Setup
The dataset used in this experiment is the “Book-
Crossing” dataset (http://www.informatik.uni-
freiburg.de/~cziegler/BX/), which contains 278,858
users providing 1,149,780 ratings about 271,379
books. Because the TPR uses only implicit user
ratings, therefore we further removed all explicit
user ratings from the dataset and kept the remaining
716,109 implicit ratings for the experiment.
The goal of our experiment in this paper is to
compare the recommendation performance and
computation efficiency between standard TPR
(Ziegler et al., 2004) and the RDF-based TPR
proposed in this paper.
The k-folding technique is applied (where k is
set to 5 in our setting) for the recommendation
performance evaluation. With k -folding, every
user u
’s implicit rating list R
is divided into 5
equal size portions. With these portions, one of them
is selected asu
’s training set
, and the rest 4
portions are combined into a test set
\
.
Totally we have five combinations
,
,
15 for user
. In the experiment, the
recommenders will use the training set
to
learn
’s interest, and the recommendation list
generated for
will then be evaluated according to
. Moreover, the size for the neighbourhood
formation is set to 20 and the number of items
within each recommendation list is set to 20 too.
For the computation efficiency evaluation, we
implemented four different versions of TPRs, each
of them is equipped with different neighbourhood
formation algorithms. The four TPR versions are:
z Standard TPR: the neighbourhood formation
method is based on comparing the target user to
all users in the dataset.
z RDF based TPR: the proposed RDF method is
used to find the neighbourhood.
z RTree based TPR: the RTree (Manolopoulos et
al., 2005) is used to find the neighbourhood.
RTree is a tree structure based neighbourhood
formation method, and it has been widely applied
in many applications.
z Random TPR: this TPR forms its
neighbourhood with randomly chosen users. It is
used as the baseline for the recommendation
quality evaluation.
The average time required by standard, RTree
based and the RDF based TPRs to make a
recommendation will be compared. We
incrementally increase the number of users in the
dataset (from 1000, 2000, 3000 until 14000), and
observe how the computation times are affected by
the increments.
In this paper, the precision and recall metric is
used for the evaluation of TPR, and its formulas are
listed below:
100|
|/|
|
(5)
100|
|/|
|(6)
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR RECOMMENDATION MAKING
17

5.2
R
Figure
b
etween
based T
P
The ho
r
charts i
n
the use
r
coordin
a
the eval
u
RDF b
a
b
oth re
c
when t
h
neighbo
u
recomm
e
p
erform
s
and the
allocate
n
Fig
u
R
esult Ana
l
4 shows t
h
the standar
d
P
R using th
e
r
izontal axis
n
dicates the
m
r
’s profile (i
a
tes imply tha
t
u
ation. It can
a
sed TPR ou
c
all and preci
h
e dissimilar
u
rhood, th
e
e
ndations
b
e
c
s
much wors
e
standard TP
R
n
eighbours f
o
u
re 4: Recomm
e
ly
sis
h
e perform
a
d
TPR and t
h
e
precision a
n
for both pre
m
inimum nu
m
.e. |
|). Th
e
t
fewer users
a
be observed
tperformed s
sion. The re
s
users are r
e
e
quality
c
ome better.
R
e
than both th
e
R
, as it is un
a
o
r target users
.
e
ndation preci
s
a
nce compa
r
h
e proposed
R
n
d recall me
t
cision and r
e
m
ber of ratin
g
e
refore large
r
a
re considere
d
that the prop
o
tandard TP
R
s
ult confir
m
s
e
moved from
of the r
e
R
Tree based
T
e
RDF based
T
a
ble to accur
a
.
s
ion and recall.
r
ison
R
DF
t
rics.
e
call
g
s in
r
x-
d
for
o
sed
R
for
that
the
e
sult
T
PR
T
PR
a
tely
ca
n
for
of
u
15
0
p
ro
acc
co
m
an
d
rec
o
RT
r
me
t
un
d
inc
r
R
D
R
D
use
r
RT
r
Ho
w
nu
m
dro
p
di
m
qu
a
lev
e
me
t
b
as
di
m
6
In
t
est
i
By
rec
o
of
qu
a
dif
f
The efficien
c
n
be seen fro
m
standard TP
R
u
sers in the
0
00 users, th
e
duce a reco
m
eptable for
m
parison, the
d
it only nee
d
o
mmendation
r
ee based TP
R
t
hod when th
d
er 8000. H
o
r
eases in th
e
F and RTre
e
F starts outp
e
r
s in the dat
a
r
ee is only e
f
w
ever, as t
h
m
ber of use
r
p
s drasticall
y
m
ensional
a
dratically in
e
l. The propo
s
t
hod because
ed, and it r
e
m
ensional vec
t
Figure 5:
A
CONCL
U
t
his
p
aper, w
e
i
mation meth
o
embeddin
g
o
mmender, n
o
the system
i
a
lity is also
f
erent from t
h
c
y evaluation
i
m
Figure 5 t
h
R
drops drasti
c
dataset incre
a
e
system nee
d
m
mendation f
o
most com
m
RDF based
T
d
s less than 4
for dataset
w
R
greatly out
p
e number of
o
wever, as
t
e
dataset, th
e
e
based TPR
e
rforms RTre
a
set is over
9
f
ficient when
h
e tree level
r
s increases)
y
because
t
vector co
m
accordance
t
s
ed RDF met
h
its indexing
s
e
duces the p
o
t
or correlatio
n
A
verage reco
m
U
SIONS
e
presented
a
o
d for recom
m
g
RDF w
i
o
t only the
c
i
s improved,
improved.
h
e clus
t
ering
i
s shown in F
i
h
a
t
, the time
e
c
ally when th
a
ses. For dat
d
s about 14 s
e
o
r a user, an
d
m
ercial syst
e
T
PR is much
seconds to
p
w
ith 15000
u
p
erforms the
users in the
d
t
he number
e
differences
becomes sm
a
e when the
n
9
000. This i
s
the
t
ree leve
l
increases (
i
RTree’s pe
r
t
he chance
m
parison
t
o the numb
e
h
od outperfor
m
s
trategy is si
n
o
ssibility for
n
computation
m
mendation tim
e
a
novel neigh
b
m
enders, na
m
i
th a TP
R
c
omputation
e
the recom
m
The RDF
m
based neigh
b
i
gure 5. It
e
fficienc
y
e number
aset with
e
conds to
d
it is not
e
ms. By
efficient,
p
roduce a
u
sers. The
proposed
d
ataset is
of users
between
a
ller, and
n
umber of
s
because
is small.
i
.e. when
r
formance
for high
increases
e
r of tree
m
s RTree
n
gle value
the high
.
e
.
b
ourhood
m
ely RDF.
R
based
e
fficiency
m
endation
m
ethod is
b
ourhood
ICEIS 2008 - International Conference on Enterprise Information Systems
18

formation methods that use offline computed
clusters as the neighbourhoods. Instead, our method
forms neighbourhood for any given target users
dynamically from scratch (thus is more accurate than
cluster based approaches) in an efficient manner. In
our experiment, it is shown that the proposed
method improves both recommendation quality and
computation efficiency for the standard TPR
recommender.
REFERENCES
awerbuch, B., Patt-Shamir, B., Peleg, D. & Tuttle, M.
(2005) Improved recommendation systems.
Proceedings of 16th Annual ACM-SIAM symposium
on Discrete algorithms. Vancouver, British Columbia.
Bentley, J. L. (1990) K-d Trees for Semidynamic Point
Sets. 6th Annual Symposium on Computational
Geometry Berkley, California, United States, ACM
Press.
Li, B., Yu, S. & Lu, Q. (2003) An Improved k-Nearest
Neighbor Algorithm for Text Categorization.
Proceedings of the 20th International Conference on
Computer Processing of Oriental Languages.
Shenyang, China.
Manolopoulos, Y., Nanopoulos, A., Papadopoulos, A. N.
& Theodoridis, Y. (2005) R-Trees: Theory and
Applications, Springer.
Sarwar, B., Karypis, G., Konstan, J. & Riedl, J. (2002)
Recommender systems for large-scale e-commerce:
Scalable neighborhood formation using clustering.
Proceedings of 5th International Conference on
Computer and Information Technology.
Schafer, J. B., Konstan, J. A. & Riedl, J. (2000) E-
Commerce Recommendation Applications. Journal of
Data Mining and Knowledge Discovery, 5, 115-152.
Ziegler, C.-N., Lausen, G. & Schmidt-Thieme, L. (2004)
Taxonomy-driven Computation of Product
Recommendations International Conference on
Information and Knowledge Management
Washington D.C., USA
Ziegler, C.-N., Mcnee, S. M., Konstan, J. A. & Lausen, G.
(2005) Improving Recommendation Lists Through
Topic Diversification. Proceedings of 14th
International World Wide Web Conference. Chiba,
Japan.
EFFICIENT NEIGHBOURHOOD ESTIMATION FOR RECOMMENDATION MAKING
19
