DISCOVERING EXPERT’S KNOWLEDGE FROM SEQUENCES OF
DISCRETE EVENT CLASS OCCURRENCES
Le Goc Marc and Benayadi Nabil
LSIS, Laboratory for Sciences of Information and Systems, UMR CNRS 6168
Aix-Marseille University, 20 Avenue Escadrille Normandie Niemmen, Marseilles cedex 20, France
Keywords:
Temporal Knowledge Discovering, Markov Process, Information Thoeory, Knowledge Based Systems.
Abstract:
This paper is concerned with the discovery of expert’s knowledge from a sequence of alarms provided by a
knowledge based system monitoring a dynamic process. The discovering process is based on the principles
and the tools of the Stochastic Approach framework where a sequence is represented with a Markov chain from
which binary relations between discrete event classes can be find and represented as abstract chronicle models.
The problem with this approach is to reduce the search space as close as possible to the relations between
the process variables. To this aim, we propose an adaptation of the J-Measure to the Stochastic Approach
framework, the BJ-Measure, to build an entropic based heuristic that help in finding abstract chronicle models
revealing strong relations between the process variables. The result of the application of this approach to a real
world system, the Sachem system that controls the blast furnace of the Arcelor-Mittal Steel group, is provided
in the paper, showing how the combination of the Stochastic Approach and the Information Theory allows
finding the a priori expert’s knowledge between blast furnace variables from a sequence of alarms.
1 INTRODUCTION
In supervised and monitored processes like produc-
tion or manufacturing processes, telecommunication
networks or web servers, a very large amount of timed
messages (alarms or simple records) are generated
and collected in databases. There is an increasing in-
terest in mining these messages to discover the un-
derlying relations between the variables that govern
the dynamic of the process and to improve its man-
agement. This problem is still an open problem (cf.
problems 2 and 3 formulated in (Mannila, 2002)) and
one of the difficulties comes from the combination of
logical relations and timed constraints (Cauvin et al.,
1998; Hanks and Dermott, 1994).
C
1
C
1
C
2
C
3
C
1
C
4
C
1
C
2
C
3
t
1
t
2
t
3
t
4
t
6
t
7
t
8
t
10
t
11
time
C
2
t
5
C
4
t
9
C
1
C
1
C
2
C
3
C
1
C
4
C
1
C
2
C
3
t
1
t
2
t
3
t
4
t
6
t
7
t
8
t
10
t
11
time
C
2
t
5
C
4
t
9
Figure 1: Example of sequence.
This paper addresses this problem in the frame-
work of the Stochastic Approach (Le Goc et al.,
2005): discovering such relations from a set of se-
quences of timed messages provided by a knowledge
based system that monitors a dynamic process. In this
framework, the messages are timed with a continu-
ous time structure clock and are considered as occur-
rences (t
k
,C
i
) of discrete event classes C
i
like in the
figure 1. A class is then a type of message (alarms,
simple records, url of a web site page, ...).
C
1
C
2
C
3
12 12
,
τ τ
− +
23 23
,
τ τ
− +
C
1
C
2
C
3
12 12
,
τ τ
− +
23 23
,
τ τ
− +
Figure 2: Example of Abstract Chronicle Model.
The Stochastic Approach considers a sequence
ω = (o
k
:: C
i
),k ∈ K = {0,...,m − 1} of m occur-
rences o
k
of discrete event classes C
i
as the observ-
able effects of a series of transition state in a timed
stochastic automata (i.e. a Markov process). A set of
timed binary relations between discrete event classes
can be deduced from this automata and represented
with abstract chronicle models as in figure 2. Such
an abstract chronicle model will come into effect
when it allows to predict most of the occurrences of
a given class. For example, if [t
2
− t
1
] and [t
10
− t
8
]
∈ [τ
−
12
,τ
+
12
], the abstract chronicle model of figure 2
can be used to predict two occurrences of the C
3
class
in the sequence of figure 1. If [t
4
− t
2
] and [t
11
− t
10
]
∈ [τ
−
23
,τ
+
23
], then the prediction is successful.
253
Goc Marc L. and Nabil B. (2008).
DISCOVERING EXPERT’S KNOWLEDGE FROM SEQUENCES OF DISCRETE EVENT CLASS OCCURRENCES.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 253-260
DOI: 10.5220/0001695702530260
Copyright
c
SciTePress

One of the problem with the Stochastic Approach
is the size of timed stochastic automata: the search
space of timed binary relations evolve exponentially
with the number of discrete event classes. There is
then a need for reducing the search space as closed
as possible to the potentially useful timed binary re-
lations. To this aim, this paper proposes to use an
adaptation of the J-measure, called the BJ-measure,
to evaluate the interestingness of hypothesis of timed
sequential binary relations.
The next section presents briefly the main works
that are related with the problem of mining a timed
data set. Section 3 introduces the basis of the Stochas-
tic Approach. Section 4 defines the BJ-measure used
to build an heuristic to prune a tree of abstract chron-
icle models. Section 5 presents the abstract chroni-
cle model discovered in 2007 with this heuristic and
shows that this result is similar to the a priori causal
knowledge an expert group formulated in 1995 about
a very complex real world process: a Sachem moni-
tored blast furnace of the Arcelor-Mittal steel group.
2 RELATED WORKS
Data Mining was developed at the confluence of re-
search in Artificial Intelligence (Machine Learning),
Statistics and database systems (refer to (Roddick and
Spiliopoulou, 2002) for a complete survey of the main
paradigms and methods for mining a sequence).
The approaches for looking for a minimum set
of association rules of the form y
1
,y
2
,...,y
n
→ x
that characterizes the relations between the data
contained in a database are mainly based on the
Apriori algorithm (Agrawal et al., 1993). This
algorithm computes the number of time a pattern
(y
1
,y
2
,...,y
n
,x) is observed in a data set. This number
is called the support. When the support of a pattern
is greater than a minimum threshold, the pattern
is considered as a potential association rule. This
characterizes the ”Frequency Approach”. When data
are timed, the data set is ordered and is called a
sequence. The adaptation of the Frequency Approach
to mine sequences takes into account the order of
a sequential pattern (y
1
,y
2
,...,y
n
,x) and leads to a
division of the ordered data set into a set of sequences
(Agrawal and Srikant, 1995). The support is then
the number of sequences containing a sequential
pattern and is used in algorithms like AprioriAll,
AprioriSome or DynamicSome. The adaptation
proposed in (Mannila et al., 1997; Hatonen et al.,
1996a; Hatonen et al., 1996b) get round the problem
of the arbitrariness of the division of an ordered
data set through a systematic division into sequences
having the same temporal length (Winepi and Minepi
algorithms). In the Temporal Reasoning domain,
(Ghallab, 1996) proposes the notion of chronicle to
represent a set of timed binary relations between
events. A chronicle is a kind of temporal pattern
specification where nodes are events and links are
timed binary constraints represented with [min, max]
intervals. Gallab’s method for discovering chronicle
models splits a set of sequences in examples and
counter examples and look for the longest patterns
that are common to the examples but not included
in the counter examples. With the FACE algorithm,
Dousson and Duong (Dousson and Duong, 1999)
adapt the Frequency Approach of (Agrawal and
Srikant, 1995) to discover frequent chronicles, but
do not propose a sound method to evaluate the timed
constraints.
The Frequency Approach generates a large
amount of relations (Roddick and Spiliopoulou,
2002) and fails at providing a global description of a
given sequence (Mannila, 2002). So measures have
been defined to evaluate the interest of the discov-
ered relations (Liu et al., 2000; Padmanabhan and
Tuzhilin, 1999; Tan et al., 2004; Vaillant et al.,
2004; Huynh et al., 2005; Bayardo and Agrawal,
1999; Hilderman and Hamilton, 2001; Jaroszewicz
and Simovici, 2001; Theil, 1970). In the Timed Data
Mining domain, the J-measure is used to evaluate the
”informativeness” of a rule (Smyth and Goodman,
1992). Let X and Y be two random variables tak-
ing a value in the respective sets X = {x
i
}
i=0,1,...,n
and Y = {y
j
}
j=0,1,...,m
. The J-measure is the amount
of mutual information shared between the variable X
and the value y
j
(Smyth and Goodman, 1992). When
denoting p(X = x
i
) ≡ p(i) and p(Y = y
i
) ≡ p( j), the
J-measure is given by the equation 1.
J(X,Y = y
j
) = p( j) ×
∑
i
p(i| j) × log(
p(i| j)
p(i)
)
≡ p( j) × j(X,Y = y
j
) (1)
The J-measure compares the posterior probability
of each rule consequent given the antecedent with the
prior probability of the consequent ( j(X,Y = y
j
)), as
done with the cross-entropy measure, but also takes
the prior probability p( j) of the antecedent into ac-
count (Roddick and Spiliopoulou, 2002), (Shore and
Johnson, 1980). The J-measure is unique, never neg-
ative and null at the independence point (Blachman,
1968). These properties explains its usage to mine se-
quences. The framework of the Stochastic Approach
(Le Goc et al., 2005; Bouch´e et al., 2005) being
ICEIS 2008 - International Conference on Enterprise Information Systems
254

closed to the Shannon’s Information Theory frame-
work (Shannon and Weaver, 1949), we propose then
to combine them to define an entropic based heuristic
for finding strong relations between variables from a
set of sequences.
3 THE STOCHASTIC APPROACH
A discrete event e
i
is a pair (x,δ
i
), where x ∈ X is
the name of a discrete variable and δ
i
∈ ∆
x
is a con-
stant. A discrete event occurrence o
k
∈ O is a tuple
(t
k
,x,δ
i
), where t
k
∈ Γ ⊆ ℜ is the time of the assig-
nation of δ
i
to x, so that o
k
≡ (t
k
,x,δ
i
) corresponds to
the assignation: x(t
k
) = δ
i
(equation 2). The occur-
rences are timed with a continuous clock structure:
∀t
k−2
,t
k−1
,t
k
∈ Γ,t
k−2
− t
k−1
6= t
k−1
− t
k
.
∀t
k
∈ ℜ,∀δ
i
∈ ∆
x
,∃t < t
k
,
x(t) 6= δ
i
∧ x(t
k
) = δ
i
⇒ o
k
≡ (t
k
,x,δ
i
)
(2)
A discrete event class C
i
= {e
i
} is an arbitrary
set of discrete events e
i
≡ (x,δ
i
). An occurrence
o
k
≡ (t
k
,x,δ
i
) of a discrete event class C
i
= {(x,δ
i
)}
is denoted either o
k
:: C
i
or o
k
≡ (t
k
,C
i
). A sequence
ω = {o
k
::C
i
}
k=0,...m−1
of discrete event class occur-
rences is an ordered set of m occurrences o
k
:: C
i
of
the set C
ω
= {C
i
} of the discrete event classes having
at least one occurrence in ω.
A timed binary relation R(C
i
,C
o
,[τ
−
,τ
+
]) is a se-
quential relation between two classes that is timed
constrained. ”[τ
−
,τ
+
]” is the time interval for ob-
serving an occurrence of the output class o
n
:: C
o
af-
ter the occurrence of the input class o
k
:: C
i
. Equa-
tion 3 defines a relation observed in a sequence ω
where d is a function returning the occurrence time
(∀o
k
≡ (t
k
,C
i
),d(o
k
) = t
k
).
R(C
i
,C
o
,[τ
−
,τ
+
]) ⇔ ∃o
n
,o
k
∈ ω,
(o
n
:: C
o
) ∧ (o
k
:: C
i
)
∧(d(o
n
) − d(o
k
) ∈ [τ
−
,τ
+
])
(3)
An abstract chronicle model is a set M = {
R
ij
(C
i
,C
j
,[τ
−
ij
,τ
+
ij
]) } of timed sequential binary
relations. For example, the abstract chronicle model
M
123
= { R
12
(C
1
,C
2
,[τ
−
12
,τ
+
12
]), R
23
(C
2
,C
3
,[τ
−
23
,τ
+
23
])
} defines two relations between three classes. This
model is represented with the ELP knowledge repre-
sentation language (Le Goc et al., 2005) in Figure 2.
A sequence ω satisfies the M
123
model when:
∃o
k
,o
n
,o
m
∈ ω,
(o
k
::C
1
) ∧ (o
n
:: C
2
) ∧ (o
m
::C
3
)
∧(d(o
n
) − d(o
k
) ∈
τ
−
12
,τ
+
12
)
∧(d(o
m
) − d(o
n
) ∈
τ
−
23
,τ
+
23
)
(4)
A path of an Elp Model is a series M = {
R(C
i
,C
i+1
,[τ
−
i
,τ
+
i
]) }, i = 0. ..n, of n timed timed bi-
nary relations (M
123
for example).
An instance ω
m
of an Elp Model M is a sequence
containing occurrences of classes which are consis-
tent with the logical and the timed constraints of
M. For example, if [τ
−
12
,τ
+
12
] = [0, 5] and [τ
−
23
,τ
+
23
] =
[3,8], the sequence { (1,C
1
), (3,C
4
), (4,C
2
), (8,C
1
),
(10,C
3
) } is an instance of the Elp Model M
123
(Fig-
ure 2) because the occurrences (1,C
1
), (4,C
2
), and
(10,C
3
) satisfy the logical and the timed constraints
of M.
Given a sequence ω, the anticipation rate (AR) of
a path M is the ratio between the number i(M) of in-
stances of M and the number i(M
′
) of instances where
M
′
is the path M minus the last timed binary rela-
tion (i.e. R(C
n−1
,C
n
,[τ
−
n−1
,τ
+
n−1
])). For example, if
i(M
123
) = 10, and i(M
12
) = 15 in a given a sequence
ω, M
12
= M
123
− R
23
(C
2
,C
3
,[τ
−
23
,τ
+
23
]), then the an-
ticipation ratio AR(M
123
) is equal to 10/15 = 66% in
ω. The cover rate CR of a path M is the ratio between
the number of instances i(M) and the number of oc-
currences of the final (output) class of M in ω. For ex-
ample, if i(M
123
) = 10 and the number of occurrences
o :: C
3
in ω is 20, then CR(M
123
) = 10/20 = 50%.
The Cover Rate is a kind of timed version of the sup-
port notion of the Frequency Approach. When a path
has an anticipation rate and a cover rate over signif-
icant thresholds, like M
123
in the example, it can be
transformed in diagnosis rules (equation 5) (Le Goc
et al., 2005). A set of paths that can be transformed
in diagnosis rules is called a signature. So, the aim
of the Stochastic Approach is to help in discovering
signatures.
∀o
k
,o
n
∈ ω
′
,
(o
k
::C
1
) ∧ (o
n
::C
2
) ∧ (d(o
n
) − d(o
k
) ∈
τ
−
12
,τ
+
12
)
⇒ ∃o
m
∈ ω
′
,(o
m
::C
3
) ∧ (d(o
m
) − d(o
n
) ∈
τ
−
23
,τ
+
23
)
(5)
When the discrete event class occurrences are in-
dependent, an ω sequence can be represented with
a homogeneous Markov chain X = (X(t
k
);k ∈ K).
To this aim, the set of discrete event classes C
ω
=
{C
i
}
i=0...n−1
of ω is confused with the state space
Q = {i}
i=0...n−1
of the Markov chain X. A binary
subsequence ω
′
= ( o
k−1
:: C
i
,o
k
:: C
j
) ⊆ ω corre-
sponds then to a state transition in X : X(d(o
k−1
)) =
DISCOVERING EXPERT’S KNOWLEDGE FROM SEQUENCES OF DISCRETE EVENT CLASS OCCURRENCES
255

i → X(d(o
k
)) = j. X being homogeneous, the transi-
tion probability from a state i to a state j is a constant
P[ j|i] ≡ P
C
j
|C
i
≡ p
ij
:
∀k ∈ K, p
ij
= P[X(t
k
) = j|X(t
k−1
) = i]
p
ij
= P
(o
k−1
:: C
i
,o
k
::C
j
) ⊆ ω|o
k−1
::C
i
(6)
A timed sequential binary relation R(C
i
,C
j
,
[τ
−
,τ
+
]) is made with a sequential relation R
s
(C
i
,C
j
)
deduced from the transition probability matrix P =
[p
ij
], the timed constraints [τ
−
,τ
+
] being computed
from the corresponding Poisson processes superpo-
sition (Le Goc, 2006). To this aim, the P matrix is
weighted in a B = [b
ij
] matrix with the probability of
the sub-sequence (o
k−1
:: C
i
,o
k
:: C
j
) in ω:
b
ij
= p
ij
× P[(o
k−1
::C
i
,o
k
:: C
j
) ⊆ ω] (7)
Given a set Ω = {ω
i
} of sequences, the role of
the BJT algorithm (Backward Jump with Timed con-
straints (Le Goc et al., 2005; Bouch´e et al., 2005))
is to compute the B matrix and the Poisson process
superposition associated with Ω. Given a maximum
depth and a maximum width, the BJT4T algorithm
(BJT for Tree) uses these representations to constitute
a tree M = {R
ij
(C
i
,C
j
,[τ
−
,τ
+
])} of the most proba-
ble timed binary relations leading to a specific output
class C
k
. The algorithm BJT4S (BJT for Signatures)
looks for the anticipating and the cover rates of each
paths of such a tree.
The problem with this method is that the num-
ber of paths contained in M = {R
ij
(C
i
,C
j
,[τ
−
,τ
+
])}
is exponential with its width. So there is a need to
define a punning method to keep only sub branches
containing strong relations between the classes.
4 THE BJ-MEASURE
According to the memoryless property of a Markov
chain, the sequential relation R
s
(C
i
,C
j
) ≡ C
i
7→ C
o
of
a timed binary relation R(C
i
,C
o
,[τ
−
,τ
+
]) between the
classes C
i
and C
o
can be view like one of the four re-
lations linking the values of two random binary vari-
ables Y = {C
i
,¬C
i
} and X = {C
o
,¬C
o
} connected
through a discrete memoryless channel ((Shannon
and Weaver, 1949), Figure 3). This means that ¬C
i
≡ C
ω
− {C
i
} and ¬C
o
≡ C
ω
− {C
o
}, so that p(C
o
|C
i
)
+ p(¬C
o
|C
i
) = 1. The basic definition of Shannon’s
condition information entropy is then directly applied
(equation 8) and an oriented J-measure can be defined
on a relation C
i
7→ C
o
.
P(C
o
|C
i
)
C
i
X
C
o
Y
¬C
i
¬C
o
P(C
o
|¬C
i
)
P(¬C
o
|C
i
)
P(¬C
o
|¬C
i
)
P(C
o
|C
i
)
C
i
X
C
o
Y
¬C
i
¬C
o
P(C
o
|¬C
i
)
P(¬C
o
|C
i
)
P(¬C
o
|¬C
i
)
Figure 3: Memoryless Channel.
H({C
o
,¬C
o
}|C
i
) =
− p(C
o
|C
i
) × log(p(C
o
|C
i
))
− p(¬C
o
|C
i
) × log(p(¬C
o
|C
i
))
= H(C
o
|C
i
) + H(¬C
o
|C
i
)
Definition 1. The occurrences of a class C
i
bring in-
formation about to the occurrences of a class C
o
if
and only if p(C
o
|C
i
) > p(C
o
).
When p(C
o
|C
i
) = p(C
o
), the occurrences of the
classes C
i
and C
o
are independent.
Definition 2. Considering a sequential binary rela-
tion C
i
7→ C
o
such that p(C
o
|C
i
) > p(C
o
), the BJ-
measure BJM(C
i
7→ C
o
) of C
i
7→ C
o
is the cross-
entropy between the occurrences of the C
i
class and
the occurrences of the set of classes { C
o
, ¬C
o
} given
by the equation 8.
BJM(C
i
7→ C
o
) = p(C
o
|C
i
) × log(
p(C
o
|C
i
)
p(C
o
)
)
+
(1−p(C
o
|C
i
))
N(C
ω
)−1
× log(
(1−p(C
o
|C
i
))
1−p(C
o
)
)
(8)
where n(C
ω
) is the number of discrete event classes
with at least one occurrence in a sequence ω and 1−
p(C
o
|C
i
) = p(¬C
o
|C
i
). The BJ-measure BJM(C
i
7→
C
o
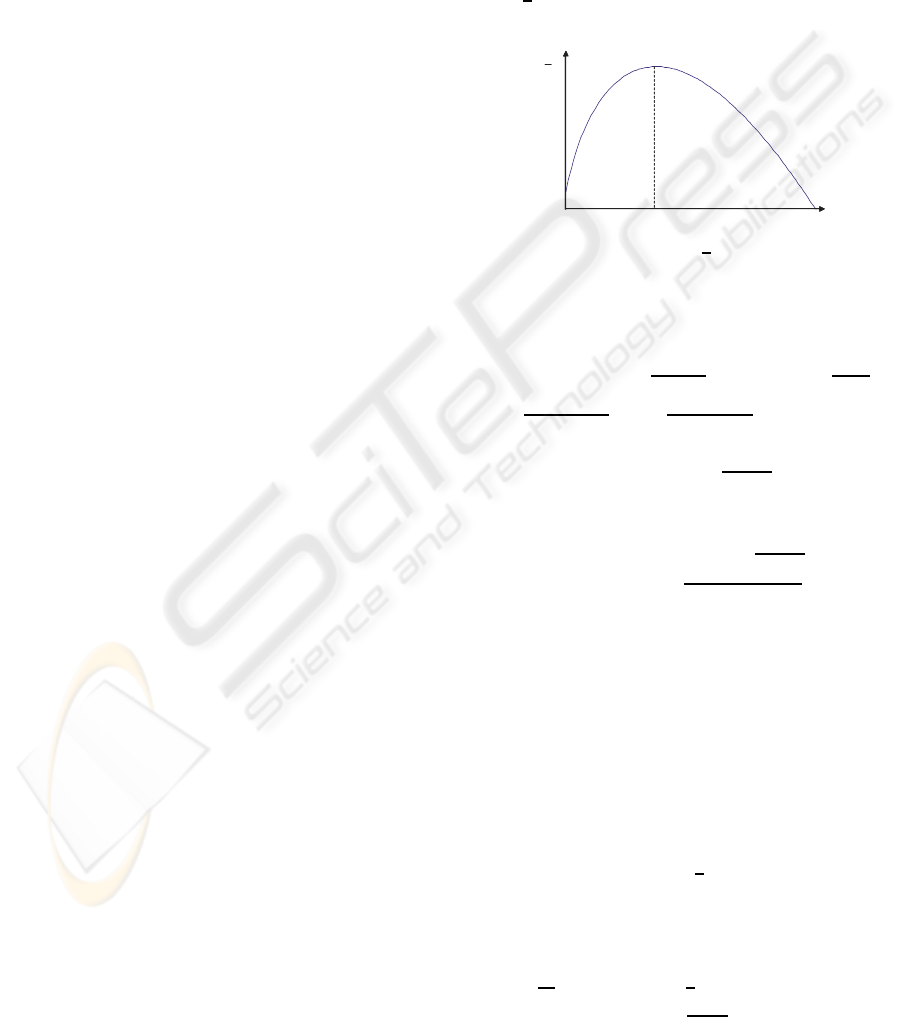
) (cf. Figure 4) is then an adaptation of the j func-
tion of the equation 1 to the P matrix of transition
probabilities of the Markov chain X corresponding to
a set of sequences Ω = {ω
i
}.
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
( )
xp
log
1
( )
yxp
( )
xp
Independency
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
( )
xp
log
1
( )
yxp
( )
xp
Independency
Figure 4: BJ-Measure.
ICEIS 2008 - International Conference on Enterprise Information Systems
256
To defines the BJ-measure of a path M = {C
i
7→
C
i+1
}
i=0...n−1
, let us consider that a sequence ω
i
=
{o
k
} of n occurrences is also a sequence of n-1 cou-
ples: ω
i
= { (o
0
,o
1
), (o
1
,o
2
), ... , (o
n−3
, o
n−2
),
(o
n−2
, o
n−1
) }. The probability of a couple (o
k−1
,o
k
)
to be an occurrence of the couple (C
i
,C
o
) is p(o
k−1
::
C
i
,o
k
:: C
o
) ≡ p(i,o). This means that ω
i
contains
p(i,o)×n occurrences of a couple (C
i
,C
o
). The prob-
ability of ω
i
will be roughly:
p(ω
i
) =
∏
i=0...n−1
(p(i,i+ 1)
p(i,i+1)×n
)
(9)
Denoting H the entropy function, we have then:
log(p(ω
i
))
= n×
∑
i=0,n−1
(p(i,i+ 1) × log(p(i,i+ 1)))
≡ n×
∑
i=0,n−1
H((i,i+ 1))
= n×
∑
i=0...n−1
(H(i) + H(i+ 1|i))
(10)
This means that the probability of a sequence is
linked with the size of the sequence and the con-
ditional entropy of the successive occurrences. The
term n×
∑
i=0...n−1
(H(i+ 1|i)) is concerned with the
P matrix of the Markov chain of ω
i
, that is to say
the probability of the series of relations M = {(C
i
7→
C
i+1
)}, i = 0... n−1. This leads to the following def-
initions:
Definition 3. The BJ-measure of a path M = {C
i
7→
C
i+1
}
i=0...n−1
exists if and only if, ∀(C
i
7→ C
i+1
) ⊆ M,
p(C
i+1
|C
i
) > p(C
i+1
).
Definition 4. When it exists, the BJ-measure of a path
M = {C
i
7→C
i+1
}
i=0...n−1
is the product of the number
of binary relations it contains with the sum of the BJ-
measure of each binary sequential relation C
i
7→ C
i+1
of M.
BJM(M) = BJM({C
i
7→ C
i+1
}
i=0...n−1
)
= n×
∑
i=0,...,n−1
BJM(C
i
7→ C
i+1
)
(11)
The quantity BJM(M) can then be interpreted as
an estimation of the quantity of information that flows
through the path M. The probability of an n-ary re-
lation M = {C
i
7→ C
i+1
}
i=0...n−1
is the probability
of the path (i,i + 1,... ,n) in the Markov chain X
corresponding to ω
i
and is given by the Chapmann-
Kolmogorov equation:
p(M) =
∏
i=0,n−1
p(C
i+1
|C
i
) (12)
By definition, the quantity P(M) decreases expo-
nentially with the number n of relations in M when
the quantity BJM(M) increases monotonically. The
idea is then to combine these quantities in order to
find a good tradeoff between the probability of a path
M and the quantity of information flowing through
it (cf. (Smyth and Goodman, 1992) for a similar
principle with the J-measure). Let us call L(M) =
P(M)×BJM(M) this quantity (Benayadi and Le Goc,
2007). The following demonstration shows that L(M)
is always limited by a convex function of the form
φ× log(
1
φ
) (Figure 5).
0.367
φ
×
φ
φ
1
log
0.367
φ
×
φ
φ
1
log
Figure 5: φ× log(
1
φ
) curve.
Demonstration 1. According to definition 2:
• ∀(C
i
7→ C
o
) ⊆ M, BJM(C
i
7→ C
o
) = α + β,
• α ≡ p(C
o
|C
i
) × log(
p(C
o
|C
i
)
p(C
o
)
), 0 < α ≤ log(
1
p(C
o
)
)
• β ≡
(1−p(C
o
|C
i
))
N(C)−1
× log(
(1−p(C
o
|C
i
))
1−p(C
o
)
), β < 0.
• So, ∀(C
i
7→ C
i+1
) ⊆ M,
BJM(C
i
7→ C
i+1
) ≤ α < log(
1
p(C
i+1
)
).
• Consequently:
BJM(M) ≤ n×
∑
i=0,n−1
log(
1
p(C
i+1
)
)
BJM(M) ≤ n× log(
1
∏
i=0,n−1
(p(C
i+1
))
)
(13)
• Rewriting p(C
i+1
|C
i
) ≡ k
i
× p(C
o
), k
i
> 1 being
a constant, the probability of the series of binary
relation of M becomes:
p(M) =
∏
i=0,n−1
p(C
i+1
|C
i
)
≡
∏
i=0,n−1
(k
i+1
) ×
∏
i=0,n−1
(p(C
i+1
))
≡ K ×
∏
i=0,n−1
(p(C
i+1
))
(14)
• Denoting φ ≡
∏
i=0,...,n−1
p(C
i+1
) and 0 < φ ≤
1, the function L(M) = p(M) × BJM(M) is
bounded:
L(M) = K × φ× log(
1
φ
) ≡ K × f(φ)
(15)
• f (φ) is a convex function that has one maximum:
∂f
∂φ
= 0 ⇔ log(
1
φ
) − 1 = 0
⇔ φ =
1
exp(1)
= 0.367
(16)
DISCOVERING EXPERT’S KNOWLEDGE FROM SEQUENCES OF DISCRETE EVENT CLASS OCCURRENCES
257
This leads to the following heuristic for pruning a
path M = {C
i
7→ C
i+1
}
i=0...n−1
when there is a sub-
path M
1
of M that maximize the quantity L:
Definition 5. Given a path M = {C
i
7→ C
i+1
}
i=0...n−1
,
M can be decomposed into tree series M
1
= {C
i
7→
C
i+1
}
i=0...n−k−1
, M
2
= {C
i
7→ C
i+1
}
i=0...n−k
and
M
3
= {C
i
7→ C
i+1
}
i=0...n−k+1
, k ≥ 1, so that:
L(M
1
) ≤ L(M
2
) > L(M
3
).
The function L(M) is an heuristic because there
is no guarantee that the first maximum is the global
maximum. This heuristic has been implemented in
the algorithm BJT4P meaning BJT for Pruning, and
the BJT4T algorithm has been modified to take into
account the condition of definition 1 so that the result-
ing trees contains branches with a no null BJ-measure.
Next section shows that this simple heuristic provides
operational results when used in a very complex real
world dynamic process: a Sachem monitored blast
furnace.
5 APPLICATION
Sachem is the name of the very large scale
knowledge-based system the Arcelor-Mittal Steel
group has developed at the end the 20th century to
help the operators to monitor, diagnose and control
the blast furnace, a very complex production process
(Le Goc, 2004; Le Goc et al., 2005)).
With a Sachem system, the blast furnace behav-
ior is described with a flow of occurrences of phe-
nomenon classes (i.e. a series of timed instances).
A phenomenon corresponds to the logical descrip-
tion of a type of physical or chemical transformation
that can occur in a blast furnace. A phenomenon is
represented with a class characterized by a name, an
identifier, a set of attributes and two times: the start
time and the end time of the phenomenon instance. A
phenomenon occurrence is then an instance of such
a class where the attributes and the times are valu-
ated by the perception function of a Sachem system.
A phenomenon occurrence is created when a behav-
ior corresponding to a particular phenomenon is rec-
ognized by Sachem (cf. (Le Goc, 2004) for exam-
ples). Sachem describes then the current behavior of
a blast furnace with a series of phenomenon occur-
rences. According to the Stochastic Approach frame-
work, when ordered by their start time, such a series is
a sequence of discrete event class occurrences where
the classes are the observed phenomena. The appli-
cation presented in this paper is concerned with the
omega variable that reveals the right or the wrong us-
age of the gas inside the blast furnace burden: any dis-
tance of the omega variable from its ideal value means
that the gas is not well used. This is a consequence of
a wrong management of the whole blast furnace. The
omega variable is a very abstract variable correspond-
ing roughly to the ratio of the number of carbon atoms
used to produce a ton of hot metal (the main blast fur-
nace output)with the number of iron (f
e
) atoms it con-
tains (the studied blast furnace produces 6,000 tons of
hot metal per day). When the omega variable is equal
to the ideal value, the blast furnace is perfectly ad-
justed: the right quantity of carbon atoms is provided
to the blast furnace to produce the required hot metal
quantity and every carbon atoms are used to only pro-
duce the f
e
atoms of the hot metal (no loss of energy).
The values of the omega variable over time are pro-
vided by a mathematical model (the MMHF model)
which is a set of 17 differential equations linking to-
gether 53 high level variables synthesizing the whole
the blast furnace behavior. This model aims at equi-
librating together a material balance and an energetic
balance that defines the function point of the blast fur-
nace.
FT
BDSS
TGS
ω
ω
ω
ω
FT
BDSS
TGS
ω
ω
ω
ω
Figure 6: Expert’s knowledge (1995).
In 1995, during the Sachem system design phase,
the Arcelor Mittal Steel group of experts defines in
a knowledge model the variables the modifications
of which cause the main modifications of the omega
variable (figure 6). These variables are the top gas
speed (TGS), the flam temperature (FT), the bur-
den permeability (BD) and the the size of the sinter
(SS) but through the burden permeability. Sachem
monitors the evolutions of these variables through a
specific set of phenomenon classes, but without any
knowledge about the causal relation between the vari-
ables TGS, FT, BD, SS and omega. Sachem marks
the observed modifications of the omega variable with
occurrences of the 1463 class corresponding to a gra-
dient of the form: omega(t) = α·t + β, α ≥ α
min
. The
studied sequence comes from Sachem at Fos-Sur-Mer
(France) from 08/01/2001 to 31/12/2001. It contains
7682 occurrences of 45 discrete event classes (i.e.
phenomena). The associated Markov chain is made of
45×45 = 2025 states. For the 1463 class linked to the
omega variable, the BJT4T algorithm is parameter-
ICEIS 2008 - International Conference on Enterprise Information Systems
258
ized to produce a tree of 5 classes depth and 20 classes
width, that is to say 20
5
= 3,200, 000 nodes. Such a
tree is very difficult to analyze handily. The BJT4P
algorithm implementing the L(M) heuristic described
in the preceding section produces a pruned tree con-
taining 195 nodes, that is to say a reduction factor of
more than 16,000. Parameterized with an anticipat-
ing ratio of 50%, the BJT4S algorithm produces the
signatures of Figure 7, where AR and CR mean re-
spectively Anticipating Rate and Cover Rate.
12171267
1718
1717
14641717
12561721
1463
1454
1216
14551267
1260
[0,35h51m6s]
[0,57h6m24s]
[0,92h0m0s]
[0,110h24m0s]
[0,132h25m30s]
[0,105h25m42s]
[0,47h14m38s]
[0,69h42m12s]
[0,103h52m56s]
[0,82h2m20s]
[0,101h5m26s]
[0,362h0m0s]
[0,445h39m48s]
1719
[0,103h52m56s]
[0,139h8m34s]
CR= 74%
AR= 62%
CR= 16%
AR= 66%
CR= 29%
AR= 152%
CR= 22%
AR= 98%
CR= 23%
AR= 139%
CR= 6%
AR= 81%
CR= 38%
AR= 71%
CR= 24%
AR= 88%
CR= 51%
AR= 118%
CR= 48%
AR= 95%
12171267
1718
1717
14641717
12561721
1463
1454
1216
14551267
1260
[0,35h51m6s]
[0,57h6m24s]
[0,92h0m0s]
[0,110h24m0s]
[0,132h25m30s]
[0,105h25m42s]
[0,47h14m38s]
[0,69h42m12s]
[0,103h52m56s]
[0,82h2m20s]
[0,101h5m26s]
[0,362h0m0s]
[0,445h39m48s]
1719
[0,103h52m56s]
[0,139h8m34s]
CR= 74%
AR= 62%
CR= 16%
AR= 66%
CR= 29%
AR= 152%
CR= 22%
AR= 98%
CR= 23%
AR= 139%
CR= 6%
AR= 81%
CR= 38%
AR= 71%
CR= 24%
AR= 88%
CR= 51%
AR= 118%
CR= 48%
AR= 95%
Figure 7: 1463 Class Signatures.
To compare this result with the a priori knowl-
edge of the experts in 1995 (figure 6), let us substi-
tutes the class with its associated variable (the omega
variable with the class 1463 for example) and trans-
form the signatures of Figure 7 in the graph of Fig-
ure 8 by merging the nodes having the same variable
name. Figure 8 contains then the relations between
the variables according to the Stochastic Approach.
The graph provided by the Expert’s in 1995 (figure
6) is included in the graph provided by the Stochastic
Approach using the BJ-measure (Figure 8). The only
difference is the direction of the relation between the
variables FT and BD. A discussion is then neces-
sary to define this difference because during the de-
velopment of Sachem, due to the rigor in the dating
method of phenomena, Sachem conclusions have lead
the experts to inverse their believes about the causal-
ity of the relation between some variables. Neverthe-
less, this result shows that when pruning the branches
bringing few information from a class to another, the
BJ-measure allows to consider only the branches with
a strong potentiality to be a signature: every signa-
tures of Figure 7 have a strong credibility according
to the laws governing the underlying process. It is to
note that the same result is observed on the Apache
system, a clone of Sachem design to monitor and di-
agnose a galvanization bath.
ω
ωω
ω
1463
1464
TGS
1454
1455
FT
1217
1216
BD
1256
1267
1260
SS
1717
1718
1721
ω
ωω
ω
1463
1464
TGS
1454
1455
FT
1217
1216
BD
1256
1267
1260
SS
1717
1718
1721
Figure 8: Variable relations (2007).
6 CONCLUSIONS
This paper proposes an adaptation of the J-measure
for pruning trees of abstract chronicle models pro-
duced according to the Stochastic Approach frame-
work: the BJ-measure. This framework provides a
global description of a set of sequences with a proba-
bility transition matrix of a Markov chain from which
the BJT4T algorithm deduces a tree of the most prob-
able abstract chronicle models. The BJ-measure al-
lows the definition of a heuristic for pruning these
trees with the aim of reducing the search space of po-
tential diagnosis rules.
This paper presents the results of the application
of this approach to a very complex real world applica-
tion, an Arcelor Mittal Steel blast furnace monitored
with a Sachem knowledge based system. The a pri-
ori expert’s knowledge about the causal relations be-
tween some blast furnace variables as formulated in
1995 has been discovered in 2007 with this approach
from a sequence of discrete event class generated by
Sachem in 2001.
Our currents works are concerned with the def-
inition of an heuristic for pruning a tree of abstract
chronicle models according to its width to improve
and generalize the usage of the BJ-measure in the
knowledge discovering process of the Stochastic Ap-
proach framework.
REFERENCES
Agrawal, R., Imielinski, T., and Swami, A. (1993). Min-
ing association rules between sets of items in large
databases. Proceedings of the 1993 ACM SIGMOD
International Conference on Management of Data,
pages 207–216.
Agrawal, R. and Srikant, R. (1995). Mining sequential pat-
terns. Proceedings of the 11th International Confer-
ence on Data Engineering (ICDE95), pages 3–14.
Bayardo, R. J. and Agrawal, R. (1999). Mining the most
DISCOVERING EXPERT’S KNOWLEDGE FROM SEQUENCES OF DISCRETE EVENT CLASS OCCURRENCES
259

interesting rules. In Proceedings of ACM KDD1999,
ACM Press, page 145154.
Benayadi, N. and Le Goc, M. (2007). Using an oriented j-
measure to prune chronicle models. To appear in the
proceedings of the 18th International Workshop on the
Principles of Diagnosis (DX07), Nashville, USA.
Blachman, N. (1968). The amount of information that y
gives about x. Information Theory, IEEE Transac-
tions, 14:27–31.
Bouch´e, P., Le Goc, M., and Giambiasi, N. (2005). Mod-
eling discrete event sequences for discovering diagno-
sis signatures. Proceedings of the Summer Computer
Simulation Conference (SCSC05) Philadelphia, USA.
Cauvin, S., Cordier, M.-O., Dousson, C., Laborie, P., L´evy,
F., Montmain, J., Montmain, M., Porcheron, M.,
Servet, I., and Trav´e, L. (1998). Monitoring and alarm
interpretation in in-dustrial environments. AI Commu-
nications ,IOS Press , 1998, pages 139–173.
Dousson, C. and Duong, T. V. (1999). Discovering chron-
icles with numerical time constraints from alarm logs
for monitoring dynamic systems. In D. Thomas, edi-
tor, Proceedings of the 16th International Joint Con-
ference on Artificial Intelligence (IJCAI-99), 1:620–
626.
Ghallab, M. (1996). On chronicles: Representation, on-line
recognition and learning. Proc. Principles of Knowl-
edge Representation and Reasoning, Aiello, Doyle
and Shapiro (Eds.) Morgan-Kauffman,, pages 597–
606.
Hanks, S. and Dermott, D. M. (1994). Modeling a dynamic
and uncertain world i: symbolic and probabilistic rea-
soning about change. Artificial Intelligence, pages 1–
55.
Hatonen, K., Klemettinen, M., Mannila, H., Ronkainen, P.,
and Toivonen, H. (1996a). Knowledge discovery from
telecommunication network alarm databases. In 12th
International Conference on Data Engineering (ICDE
’96). New Orleans, LA, pages 115–122.
Hatonen, K., Klemettinen, M., Mannila, H., Ronkainen, P.,
and Toivonen, H. (1996b). Tasa: Telecommunica-
tion alarm sequence analyzer, or how to enjoy faults
in your network. In IEEE Network Operations and
Management Symposium (NOMS ’96). Kyoto, Japan,
pages 520–529.
Hilderman, R. and Hamilton, H. (2001). Knowledge dis-
covery and measures of interest. Kluwer Academic
publishers.
Huynh, X.-H., Guillet, F., and Briand., H. (2005). Arqat:
An exploratory analysis tool for interestingness mea-
sures. In Proceedings of the 11th international sympo-
sium on Applied Stochastic Models and Data Analysis
ASMDA-2005, page 334344.
Jaroszewicz, S. and Simovici, D. A. (2001). A general
measure of rule interestingness. In Proceedings of
PKDD2001, Springer-Verlag, page 253265.
Le Goc, M. (2004). Sachem, a real time intelligent diagno-
sis system based on the discrete event paradigm. Sim-
ulation, The Society for Modeling and Simulation In-
ternational Ed., 80(11):591–617.
Le Goc, M. (2006). Notion d’observation pour le diagnostic
des processus dynamiques: Application `a Sachem et
`a la d´ecouverte de connaissances temporelles. Hdr,
Facult´e des Sciences et Techniques de Saint J´erˆome.
Le Goc, M., Bouch´e, P., and Giambiasi, N. (2005). Stochas-
tic modeling of continuous time discrete event se-
quence for diagnosis. 16th International Workshop on
Principles of Diagnosis (DX’05) Pacific Grove, Cali-
fornia, USA.
Liu, B., Hsu, W., Chen, S., and Ma, Y. (2000). Analyz-
ing the subjective interestingness of association rules.
IEEE Intelligent Systems, page 4755.
Mannila, H. (2002). Local and global methods in data min-
ing: Basic techniques and open problems. 9th Interna-
tional Colloquium on Automata, Languages and Pro-
gramming, Malaga, Spain,, 2380:57–68.
Mannila, H., Toivonen, H., and Verkamo, A. I. (1997). Dis-
covery of frequent episodes in event sequences. Data
Mining and Knowledge Discovery, pages 259–289.
Padmanabhan, B. and Tuzhilin, A. (1999). Unexpectedness
as a measure of interestingness in knowledge discov-
ery. Decision Support Systems, pages 303–318.
Roddick, J. and Spiliopoulou, M. (2002). A survey of tem-
poral knowledge discovery paradigms and methods.
IEEE Transactions on Knowledge and Data Engineer-
ing, 14:750–767.
Shannon, C. and Weaver, W. (1949). The mathematical the-
ory of communication. University of Illinois Press,
27:379–423.
Shore, J. and Johnson, R. (1980). Axiomatic derivation of
the principle of maximum entropy and the principle
of minimum cross-entropy. Information Theory, IEEE
Transactions, 26:26–37.
Smyth, P. and Goodman, R. M. (1992). An information
theoretic approach to rule induction from databases.
IEEE Transactions on Knowledge and Data Engineer-
ing 4, page 301316.
Tan, P.-N., Kumar, V., and Srivastava, J. (2004). Selecting
the right objective measure for association analysis.
Information Systems, 29(4):293–313.
Theil, H. (1970). On the estimation of relationships involv-
ing qualitative variables. American Journal of Sociol-
ogy, pages 103–154.
Vaillant, B., Lenca, P., and Lallich, S. (2004). A clustering
of interestingness measures. In Proceedings of the 7th
International Conference on Discovery Science, pages
290–297.
ICEIS 2008 - International Conference on Enterprise Information Systems
260
