CONGESTION CONTROL SYSTEM WITH PID CONTROLLER
USING FUZZY ADAPTATION MECHANISM
Magdalena Turowska
Institute of Computer Science and Engineering, Wroclaw University of Technology
Wyb. Wyspiańskiego 27, 50-370 Wroclaw, Poland
Keywords: Congestion control, fuzzy inference system, PID controller, adaptation mechanism.
Abstract: The congestion control in computer network is a problem of controlling a specific object such as a computer
network. The paper provides an adaptation mechanism designed to prevent unstable behavior of the system,
with fuzzy rules, and with an inference mechanism that identifies the possible sources of nonlinear behavior.
The adaptation mechanism can be designed to adjust PID controller tuning parameters when oscillatory
behavior is detected. Tests in nonlinear and uncertainty process are performed.
1 INTRODUCTION
The congestion control is essential for ensuring the
appropriate quality of service for network users.
This problem plays a significant role in designing
and using computer networks. At the same time, the
congestion control constitutes a current research
issue, with a constantly growing number of
publications (Imer and Basar 2001; Misra, Gong and
Towsley; Turowska 2004; 2007).
The paper provides an adaptation mechanism
designed to prevent unstable behavior, with fuzzy
rules, and with an inference mechanism that
identifies the possible sources of nonlinear behavior
of computer network. The adaptation mechanism
can be designed to adjust PID controller tuning
parameters when oscillatory behavior is detected.
2 MODEL OF THE CONTROL
SYSTEM
TCP congestion control dynamics with an AQM
(Active Queue Management) can be modelled as a
feedback system (Figure 1). This system consists of
a desired queue length at a router, denoted by
*
y ; a
queue length at a router as a controlled variable
y ; a
plant that represents a combination of subsystems
such as TCP sources, routers, and TCP receivers that
send, process, and receive TCP packets,
respectively; an AQM controller, which controls the
packet arrival rate to the router queue by generating
packet drop probability as a control signal
u ; and a
feedback signal
y (the queue length) used to obtain
the control error term
yy −=
*
ε .
Controller
u
*y
ε
y
+
-
Plant
Figure 1: A feedback control model of TCP/AQM.
In Misra, Gong and Towsley 2000 a dynamic
model for TCP congestion control, delays, and
queues is expressed by the transfer function:
sd
P
e
dss
sK
−
++
=
)1)(1(
)(
α
β
(1)
where
d
is the round-trip delay,
2
3
4N
C
=
β
,
N
Cd
2
2
= α
,
C
is the bottleneck link capacity, and
N
is the number of TCP connections.
To regulate the queue length at a router around a
desired value
*
y a controller having the ability to
predict and adjust control performance is required.
This can be achieved by using the PID controller
(Fan, Ren and Lin 2003). The transform function of
PID controller has a form
504
Turowska M. (2008).
CONGESTION CONTROL SYSTEM WITH PID CONTROLLER USING FUZZY ADAPTATION MECHANISM.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 504-507
DOI: 10.5220/0001701405040507
Copyright
c
 SciTePress

sk
s
k
ksK
D
I
PC
++=)(
. (2)
To tune parameters
P
k
,
I
k
, and
D
k
of the PID
controller we analyse the stability of the closed loop
system with the plant (1) and the controller (2).
Using frequency response techniques it can be
established that marginal stability is obtained when
1|)(| =
ω
iK
OL
and
π
ω
±
=)(arg iK
OL
where
)()()( sKsKsK
cPOL
=
is the open loop
transfer function. For the system (1), (2) the solution
for marginal stability is given by
1|
)1)(1(
))((
|
2
=
++
++
− di
DIP
e
dii
ikkik
ω
ωωα
ωωβ
(3)
and
π
ωωα
ωωβ
ω
±=
++
++
−
)
)1)(1(
))((
arg(
2
di
DIP
e
dii
ikkik
. (4)
If the controller tuning is fixed and the degrees
of freedom are granted to parameter
α
from (3) and
(4) we can calculate
u
α
and
u, α
ω
, the value of
parameter
α
that leads the closed loop response to
marginal stability and the frequency of such
oscillations. If similar analysis are performed,
granting degrees of freedom to
β
calculating its
frequency, and next to
d
, the set of values
u, α
ω
,
u, β
ω
and
ud ,
ω
will be obtained for a given
controller tuning. This frequencies can be called as
the characteristic ultimate frequencies for a given
process parameter.
The parameters that can be identified from the
observed oscillatory behavior of the system response
are the damped natural frequency,
ω
, and the
damping ratio,
ζ
. These parameters will indicate
how oscillatory the response is and what is cause of
such oscillation, and can be calculated from a
dynamic analysis of the closed-loop system
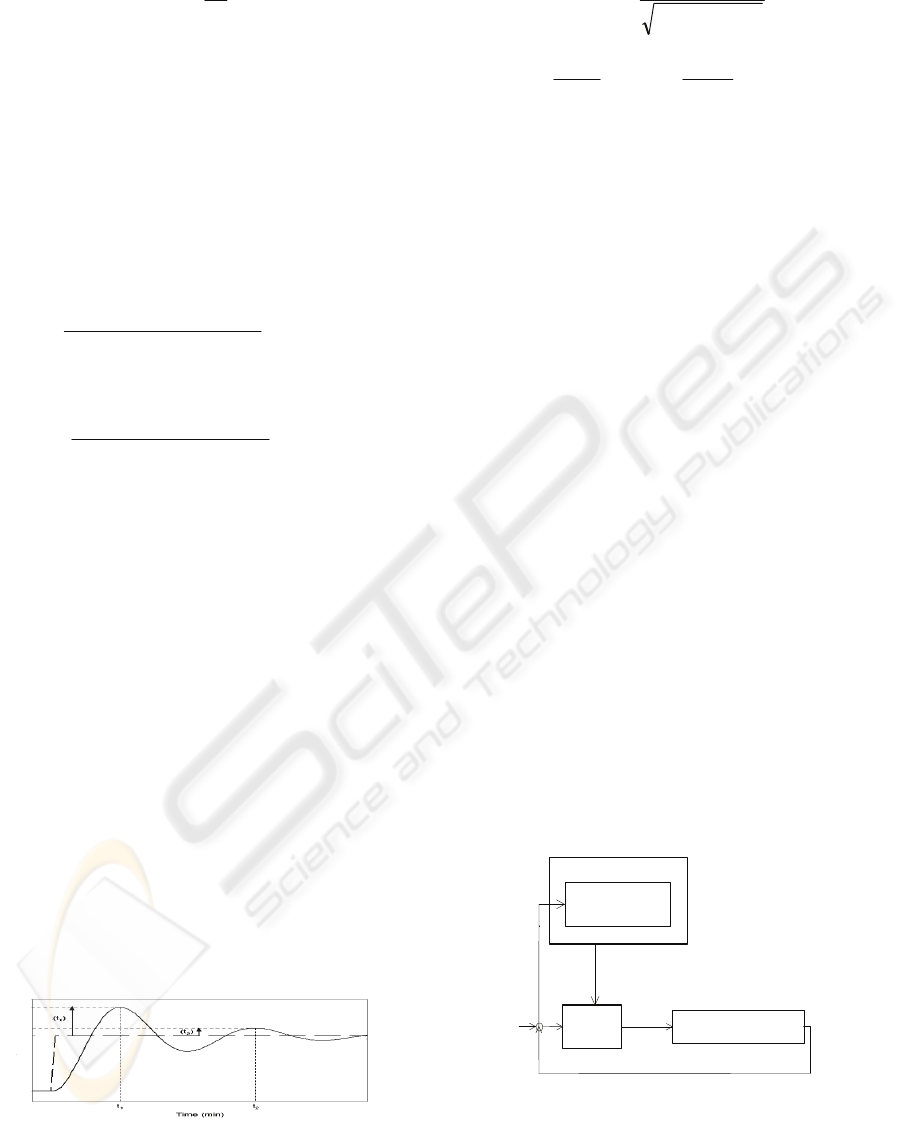
response, like the one presented in Figure 2.
Figure 2: A response of the system under consideration.
The damping ratio
ζ
can be calculated as
(Marlin, 2000):
)(ln4
)ln(
22
A
A
+
=
π
ζ
, (5)
where
)(
)(
1
2
tO
tO
A =
and
12
2
tt −
=
π
ω
.
By measuring
)(
1
tO
,
1
t
,
)(
2
tO
and
2
t
as indicated
in Figure 2 we can calculate
ω
and
ζ
.
An oscillatory behavior is obtained for
]1,1[
−
∈
ζ
. The damping ratio equal to 1 is a
critically damped system, with no oscillatory
behavior,
ζ
equal to 0.7071 is a system with
approximate 5% overshoot, which we will consider
an optimal response, 0 leads to a marginally stable
response (sinusoidal behavior), less than 0 leads to
unstable behavior.
3 FUZZY ADAPTATION
MECHANISM
When a PID controller operates with non-optimal
tuning and in nonlinear environment two different
behaviors can occur: slow compensation for
disturbances or setpoint changes, or presence of
undesired oscillatory behavior. The presence of such
oscillations is usually more damaging since not only
diminishes the computer network (the control
system) performance but also causes the network
degradation.
Additional information may be used to gradual
improving of basic control algorithm (PID). The
improving is needed in order to adapt the basic
control algorithm to the control plant. The structure
of the system with adaptation is presented in
Figure 3.
PID
u
*y
ε
y
+
-
control plant
adaptation mechanism
fuzzy inference
system
DIP
kkk ,,
Figure 3: Block diagram of the closed-loop system with
adaptation mechanism.
The proposed adaptation mechanism uses a two-
input-three-output fuzzy inference system. The input
linguistic variables are damping ratio and damped
O
O
*
y
CONGESTION CONTROL SYSTEM WITH PID CONTROLLER USING FUZZY ADAPTATION MECHANISM
505

natural frequency. The output linguistic variables are
the change factors
P
g
,
I
g
and
D
g
of control
algorithm (PID regulator). We have used triangular
shaped membership functions for damping ratio
ζ
and the damped natural frequency
ω
, and for the
change factors.
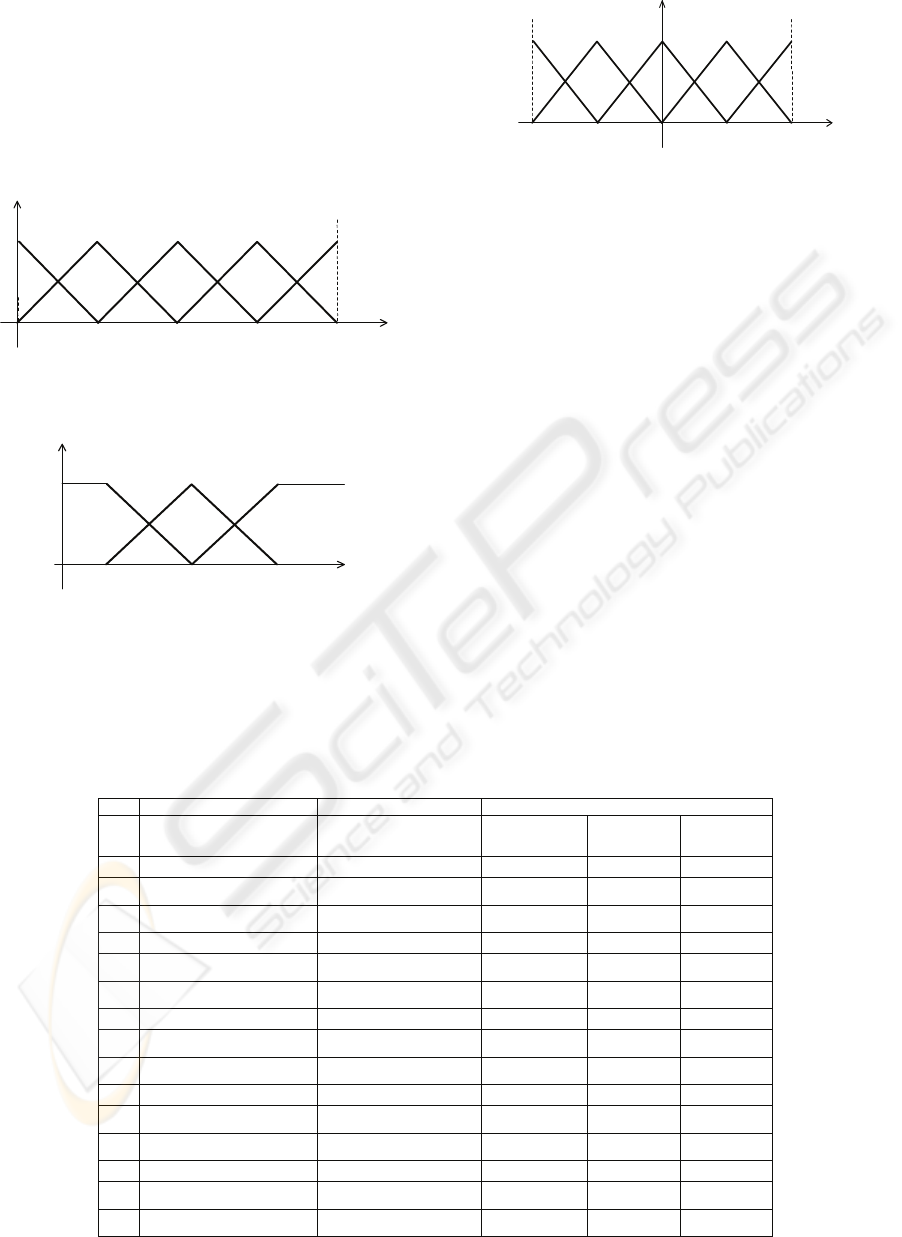
Figure 4, 5 and 6 show the membership
functions of the input and output variables.
very-slowslow
optimal
1
membership function
-1
fast
very-fast
ζ
0.707100.85
Figure 4: Membership function of the linguistic
representing the damping ratio
ζ
.
membership function
ω
u, α
ω
ud ,
ω
u, β
ω
related− α
related−d
0
related−
β
Figure 5: Membership function of the linguistic
representing the damped natural frequency
ω
.
big posi t ivesmall positive
zero
1
membership function
-1
small negati ve
big negative
change fact or
Figure 6: Membership function of the linguistic
representing the output variables
P
g
,
I
g
and
D
g
.
A fuzzy inference is designed to operate on
damping ratio
ζ
and the damped natural
frequency
ω
, and uses linguistic rules to determine
the change factors. The proposed rules are shown in
Table 1.
For the implementation of the fuzzy inference
system we have used the computationally simple and
most widely chosen methods: singleton
fuzzification, Mamdani’s product rule of
implication, and the centroid of area (CoA) method
of defuzzification.
Once the fuzzy inference system has calculated the
change factors, based on the nonlinear behavioral
pattern that was identified, such value is used to
obtain the new set of controller parameters
P
k
,
I
k
,
and
D
k
.
The new values of controller parameters are set as
)1(
, PprPP
gkk +=
,
)1(
, IprII
gkk +=
and
)1(
, DprDD
gkk
+
=
, where
prP
k
,
,
prI
k
,
,
prD
k
,
are the previous values of controller parameters.
Table 1: Fuzzy rules used in the inference system.
IF AND THEN
the damping ratio
ζ
the damped natural
frequency
ω
P
g
I
g
D
g
1 very fast
α
− related
BN Z Z
2 very fast
β
− related
BN BP SP
3 very fast
d
− related
BN BP BP
4 fast
α
− related
SN Z Z
5 fast
β
− related
SN SP Z
6 fast
d
− related
SN Z SP
7 optimal
α
− related
Z Z Z
8 optimal
β
− related
Z Z Z
9 optimal
d − related
Z Z Z
10 slow
α
− related
SP Z Z
11 slow
β
− related
SP
SN SN
12 slow
d
− related
SP
Z Z
13 very slow
α
− related
BP Z Z
14 very slow
β
− related
BP SN SN
15 very slow
d
− related
BP SN BN
ICEIS 2008 - International Conference on Enterprise Information Systems
506

4 SIMULATIONS RESULTS
In order to evaluate the performance of the fuzzy
adaptation mechanism under consideration we
carried out the number of simulation in Matlab 6.0
and Simulink 3.0. We compare the control
performance of the system that use the PID
controller and fuzzy adaptation mechanism with that
of the PID controller only. In the PID controller, we
use the parameters
P
k
,
I
k
, and
D
k
calculated in
Fan, Ren and Lin 2003.
We used the network topology shown in
Figure 7.
source 2
destination
router
source 1
source 3
60 Mb/s
60 Mb/s
60 Mb/s
100 Mb/s
Figure 7: Network topology used for the simulation.
The results of simulations for conventional PID
and fuzzy PID (PID with fuzzy adaptation)
algorithms are shown in Figures 8 and 9.
The goodput presented in Fig. 8 is the ratio of
the total number of nonduplicate packets received at
all destinations per unit time to link capacity. System
with fuzzy adaptation of PID achieves a higher
goodput than conventional PID.
Figure 8: Goodput versus simulation time for both fuzzy
PID and conventional PID.
As can be seen from Fig. 9 the queue length is
regulated around the target value 100 packets for
both fuzzy PID and PID algorithms. For
conventional PID we have observed the higher
magnitude of overshoots.
Figure 9: Queue length versus simulation time for both
fuzzy PID and conventional PID.
The performance specification of system with fuzzy
adaptation mechanism is better than the performance
of system with conventional PID controller.
5 CONCLUSIONS
This paper presents the problem of fuzzy adaptation
in the congestion control system with PID controller
in TCP network.
The fuzzy mechanism has been tested in
simulations. Simulation results show that the system
with the proposed fuzzy inference system has better
performance and queue length behavior than system
with the conventional PID. The future work can
include the design of mechanism, which can tune the
parameters of membership functions on line, using
measurements from the network, to obtain even
better behaviour.
REFERENCES
Fan, Y., Ren, F., Lin C., 2003. Design a PID Controller for
Active Queue Management, Proceedings of the Eight
IEEE International Symposium on Computers and
Communication, pp. 985-990.
Imer, O., Basar, T., 2001. Control of congestion in high
speed networks, Eur. J. Contr., 7, pp. 132-144.
Marlin, T., 2000. Process Control. Designing Processes
and and Control Systems for Dynamic Performance .
McGraw-Hill, New York, USA.
Misra, V., Gong, W., Towsley, D., 2000. Fluid-based
analysis of a network of AQM routers supporting TCP
flows with an application to RED, Proceedings of
ACM SIGCOMM, pp. 151-160.
Sanjuan, M., Kandel, A., Smith., C. A., 2006. Design and
implementation of a fuzzy supervisor for on-line
compensation of nonlinearities: An instability
avoidance module. Engineering Applications of
Artificial Intelligence, 19, pp. 323-333.
Turowska, M., 2004. Application of uncertain variables to
stability analysis and stabilization for ATM ABR
congestion control systems, Proceedings of the
International Conference on Enterprise Information
Systems. INSTICC Press, Porto, 2, pp. 523-526.
Turowska, M., 2007. Fuzzy congestion control in Internet,
Proceedings of the 16th International Conference on
Systems Science, Wroclaw, Poland, 2, pp. 347-354.
CONGESTION CONTROL SYSTEM WITH PID CONTROLLER USING FUZZY ADAPTATION MECHANISM
507