
OPTIMAL LAYOUT SELECTION USING PETRI NET IN AN
AUTOMATED ASSEMBLING SHOP
Iraj Mahdavi
1
, Mohammad Mahdi Paydar
1
, Babak Shirazi
1
and Magsud Solimanpur
2
1
Department of Industrial Engineering, Mazandaran University of Science & Technology, Babol, Iran
2
Urmia University, Urmia, Iran
Keywords: Petri net, Automated assembling shop, Production cycle time, WIP.
Abstract: Abstract In today's competitive manufacturing systems, it is crucial to respond quickly to the demand of
customers and to decrease total cost of production. To achieve higher performance of automated assembling
shop, it is needed to utilize methods to minimize production cycle time (makespan) and work-in-process
(WIP) in buffers. This paper intends to focus on the selection of optimal layout based on allocation of
machines to different locations as they can perform similar operations with different processing times. The
time Petri net (TPN) has been used to illustrate the applications of proposed model in case study.
1 INTRODUCTION
Layout designing have been extensively researched
in many manufacturing systems. Researches have
mainly concentrated on the important class of
systems called flow shops, in which components are
moved linearly through the system, and
manufacturing stations are totally dedicated (Adel
and Baz, 2004). Now a days, automatic tools such as
computer numerical control (CNC) machines and
different types of robots have been used in assembly
lines called automated assembling shop. Automated
assembling shop consists of several types of CNC
machines, robots, and automated guided vehicles
designed to produce a great variety of products in
multiple lines. Many products can be manufactured
and assembled in automated assembling shop. The
parts to be assembled are transferred by conveyors
and robots. Robots transfer the parts from the
conveyors to buffer. The main problem of designing
an automated assembling shop is to obtain the
minimum production cycle time and WIP (Hsieh et
al, 2007).
In the literature, this problem is most often
treated as a single objective problem and only the
capacity constraints of the assembly shop are
considered. For example, Boubekri and Nagaraj
(1993) developed an integrated approach for the
selection and design of assembly systems. A model
for evolutionary implementation of efficient
assembly systems was proposed by Rampersad
(1994, 1995). But very little has been reported on
the design of assembly systems and system layout.
Due to the discrete nature, Petri nets (PN) are
widely used for modeling manufacturing systems
(Park et al., 2001, Yan et al., 2003). Petri net is a
graphical and mathematical modeling tool for
describing and studying systems (Jehng, 2002). In
the early development of Petri nets (Petri, 1962) and
(Peterson, 1981), it was particularly concerned with
the description of the causal relationships between
events. Much of the early theory, notation, and
representation of Petri nets have been developed for
discrete event systems. (Ramchandani, 1974)
showed how Petri nets could be applied to the
modeling and analysis of systems of concurrent
components. There have been reports of Petri nets
applications in the representation, analysis and
control of flexible assembling system/ flexible
manufacturing system (Alla et al., 1984), (Cecil et
al., 1992), (Muro-Medrano et al., 1992), and
(Moore, 1996). Petri nets have been used to model
robotic or assembly processes so that a sequence of
operations is generated based on the Petri net model.
On the other hand, many attempts have also been
made to extend and modify conventional Petri nets
to enhance their modeling power for assembly
systems. This resulted in net variations such as
colored Petri nets, control nets, timed Petri nets, and
object Petri nets. This paper focuses on the layout
519
Mahdavi I., Mahdi Paydar M., Shirazi B. and Solimanpur M. (2008).
OPTIMAL LAYOUT SELECTION USING PETRI NET IN AN AUTOMATED ASSEMBLING SHOP.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 519-523
DOI: 10.5220/0001703905190523
Copyright
c
SciTePress

designing in automated assembling shops. Since
some machines can perform different operations in
different processing times, the machines are
allocated to different locations so that the total
production cycle time and WIP are minimized.
2 PETRI NET MODELING
A timed-PN is able to describe a time dependent
system. Two methods exist to model timing: either
timing associated with places (the PN is said to be
place-timed Petri net, or P-timed PN), or timing
associated with transitions (the PN is said to be
transition-timed Petri net, or T-timed PN). It also
can be shown that P-timed PNs and T-timed PNs are
equivalent, and it is possible to move from one
model to the another (Zhang et al., 2005).
This paper addresses a production system that
receives an order from customers. According to the
order, an initial layout and machine allocation of
production line is designed. The automated
assembling shop for this model consists of two
conveyor robots (R
'
, R
"
). There are nine machines
(M1, M2,..., M9), five work pieces (A, B, C, D, E)
and fourteen operations (OP
1,
OP
2
,..., OP
14
). We
consider five buffers in the layout such that their
amount of WIP is different. Figure 1 is a graphical
representation of material flow in the manufacturing
system based on the above information. The
machines M
2
, M
3
and M
8
can perform either of
operations OP
2
, OP
3
and OP
12
in different
processing times. The problem is to find the
optimum allocation of these machines for doing
these operations to minimize the total production
cycle time and WIP.
Figure 1: System configuration of automated assembeling
shop.
Figure 2 shows a specific allocation of these
machines in which operations OP
2
, OP
3
and OP
12
are performed by machines M
2
, M
3
and M
8
,
respectively.
Figure 2: The OPC of automated assembling shop.
In Figure 2, the Operation Process Chart (OPC) of
the manufacturing system is shown. The OPC is
used for showing the procedure through which work
pieces are assembled and all operations in the
process of manufacturing system. In OPC,
purchased work piece (work piece D) is connected
to the basic line (work piece C) by a horizontal line.
The operations that are connected to the basic line
by dash line (OP
7,
OP
8
) represent tool changing in
machine M
5
.
2.1 P-timed PN Model of Automated
Assembling Shop
For the PN model of automated assembling shop
shown in Figure 3. Place-timed Petri nets (P-timed
PN) are used to model the system, in which
transitions represent events and the places represent
states, or conditions.
Figure 3: The PN model of automated assembling shop.
ICEIS 2008 - International Conference on Enterprise Information Systems
520
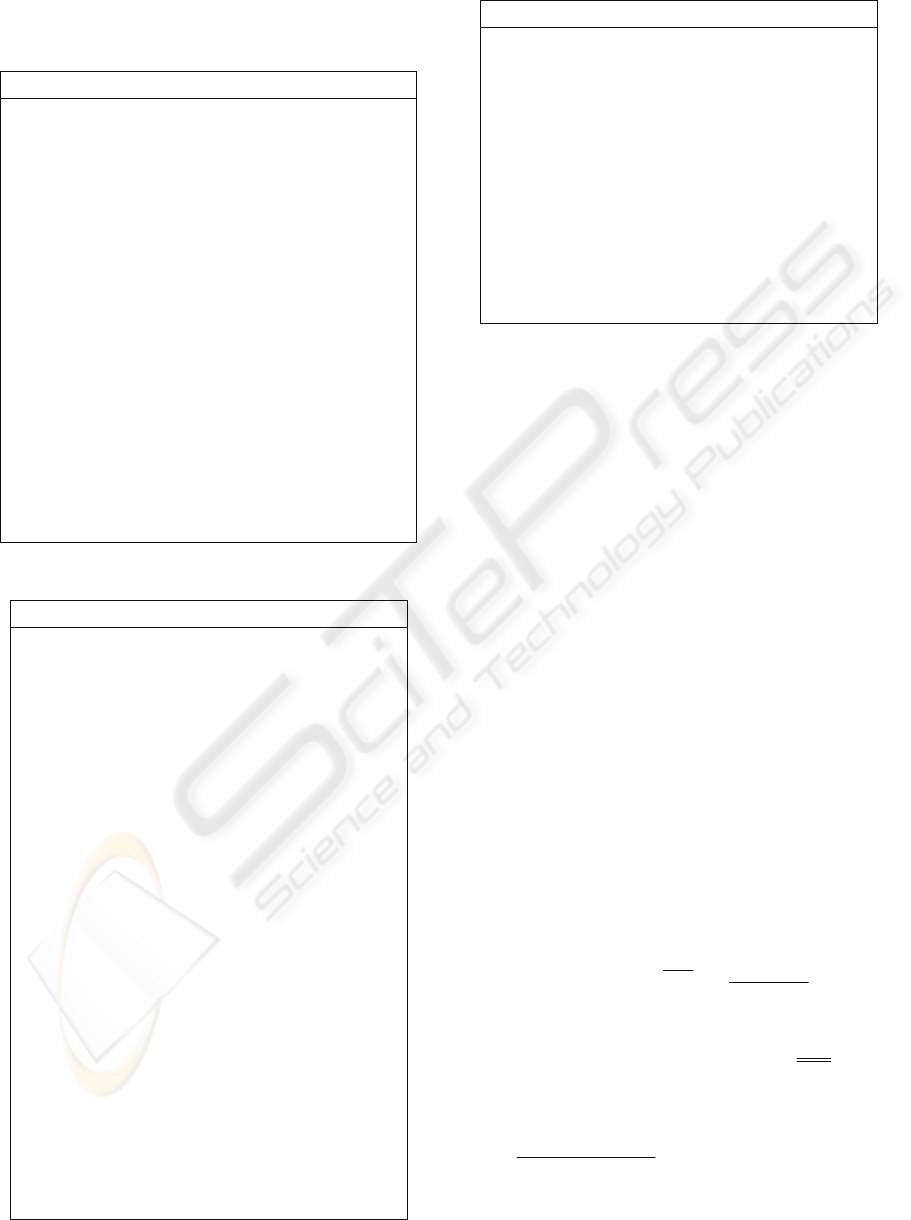
The role of transitions and places in the proposed
PN model are shown in Tables 1 and 2, respectivly.
Table 1: Role of transitions in the proposed PN model.
Transitions
t
1
: Operation OP
1
starts
t
2
: Operation OP
1
finishes
t
3
: Operation OP
2
starts
t
4
: Operation OP
2
finishes
t
5
: Operation OP
3
starts
t
6
: Operation OP
3
finishes
t
7
: Operation OP
4
starts
t
8
: Operation OP
4
finishes& Operation OP
5
starts
t
9
: Operation OP
5
finishes
t
10
: Operation OP
6
starts
t
11
: Operation OP
6
finishes& Operation OP
7
starts
t
12
: Operation OP
7
finishes& Operation OP
9
starts
t
13
: Operation OP
8
finishes
t
14
: Operation OP
9
finishes& Operation OP
8
starts
t
15
: Operation OP
10
starts
t
16
: Operation OP
10
finishes & Operation OP
11
starts
t
17
: Operation OP
12
starts
t
18
: Operation OP
12
finishes& Operation OP
13
starts
t
19
: Operation OP
13
finishes
t
20
: Operation OP
11
finishes& Operation OP
14
starts
t
21
: Operation OP
14
finishes
Table 2: Role of places in the proposed PN model.
Places
p
1
: Work piece A available
p
2
: Operation OP
1
p
3
: Machine M1 available
p
4
: Work piece A ready for the operation OP
2
p
5
: Buffer of work piece A available
p
6
: Operation OP
2
p
7
: Machine M2 available
p
8
: Work pieces A available to assemble
p
9
: Work piece B available
p
10
: Operation OP
3
p
11
: Machine M3 available
p
12
: Work piece A ready for the operation OP
4
p
13
: Buffer of work piece B available
p
14
: Operation OP
4
p
15
: Machine M4 available
p
16
: Operation OP
5
p
17
: Robot R
/
available
p
18
: Work piece B ready for the assemble
p
19
: Buffer of work piece B available
p
20
: Work piece C available
p
21
: Operation OP
6
p
22
: Operation OP
7
p
23
: Machine M5 available
p
24
: Operation OP
8
p
25
: Operation OP
9
p
26
: Work piece C ready for the operation OP
10
p
27
: Buffer of work piece C available
p
28
: Operation OP
10
Table 2: Role of places in the proposed PN model(cont).
Places
p
29
: Machine M6 available
p
30
: Work piece D available
p
31
: Operation OP
11
p
32
: Machine M7 available
p
33
: Work piece E available
p
34
: Operation OP
12
p
35
: Machine M8 available
p
36
: Robot R
//
available
p
37
: Operation OP
13
p
38
: Buffer of work piece E available
p
39
: Work piece E ready for to assemble
p
40
: Operation OP
14
p
41
: Machine M9 available
p
42
: Final product available
3 PROPOSED METHOD TO
SELECT OPTIMAL LAYOUT
The production cycle time is obtained by MATLAB
Petri net toolbox. The maximum WIP (WIP
max
) is
calculated according to the maximum number of
tokens in buffer places (p
4
, p
12
, p
18
, p
26
, p
39
). The
average work-in-process (WIP
average
) for each buffer
can be obtained as discussed below.
We define the following notation:
i : is the number of work pieces
()
1, 2,....,iN=
j : is the number of buffers
()
1, 2,....,jM=
t : is the discrete unit time
()
1, 2....,tT=
k : is the number of allocations
()
1, 2,...,kL=
Decision Variable:
1 If work piece is in buffer at time
0Otherwise
ijt
ijt
W
⎧
=
⎨
⎩
According to the notations, we obtain the WIP
average
of j
th
buffer for each state as given in equation (1).
()
()
11
NT
ijt
it
average
j
j
W
WIP WIP
T
==
==
∑∑
(1)
We calculate the average WIP of buffer j among all
the allocations as given in equation (2).
(
)
111
Average W IP within all allocations WIP
j
LNT
ijt
kit
k
W
TL
===
==
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
∑∑∑
(2)
OPTIMAL LAYOUT SELECTION USING PETRI NET IN AN AUTOMATED ASSEMBLING SHOP
521

For allocation k, we calculate the value
()
k
z
F
as a
decision criterion for selection of optimum
allocation as given in equation (3).
()
()
(
)
zxy
k
k
k
FFF=+ : (3)
where
()
()
(
)
2
1
2
111
11
1
M
xj
k
j
j
j
LNT
NT
ijt
ijt
M
kit
it k
j
j
FCWIPWIP
W
W
C
TTL
=
===
==
=
⎛⎞
=−=
⎜⎟
⎝⎠
⎛⎞
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎜⎟
−
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
∑∑∑
∑∑
∑
.
()
()
minyTk
k
FCTT=−
.
C
j
: is the cost coefficient of buffer j.
C
T
: is the cost coefficient of production cycle time.
1
1
M
jT
j
CC
=
+
=
∑
.
T
k
: is the makespan of allocation k.
min
T : is the minimum makespan among all the
allocations.
Finally, the allocation with minimum
F
z
is selected.
4 COMPUTATIONAL RESULTS
Assume that ten products are to be produced in the
manufacturing system discussed above. Table 3
shows six possible allocations of machines M
2
, M
3
and M
8
for doing operations OP
2
, OP
3
and OP
12
.
Table 3: Possible allocations of machines M
2
, M
3
and M
8
for operations OP
2
, OP
3
and OP
12
.
Operation
Allocation
OP
2
OP
3
OP
12
1 M
3
M
2
M
8
2 M
3
M
8
M
2
3 M
2
M
8
M
3
4 M
2
M
3
M
8
5 M
8
M
2
M
3
6 M
8
M
3
M
2
The simulation results of WIP in each buffer and the
production cycle time of each allocation have been
given in Tables 4 and 5, respectively.
As a managerial consideration, let us assume that
the cost coefficient value of production cycle time is
0.4, i.e. C
T
= 0.4, and the cost coefficient value of
each buffer is as shown in Table 6.
Table 4: The average and maximum WIP of each buffer in
different allocations.
Allocation
Buffe
r
1 2 3 4 5 6
WIP
ave
4.8 4.8 3.3 3.3 1.6 1.6
1
WIP
max
11 11 8 8 5 5
WIP
ave
3.4 3.7 3.1 1.7 1.7 0.7
2
WIP
max
7 8 7 4 5 2
WIP
ave
0 0 0.01 0.01 0.7 0.7
3
WIP
max
0 0 1 1 2 2
WIP
ave
1.6 1.6 0.3 0.3 0.1 0.8
4
WIP
max
3 3 1 1 1 1
WIP
ave
4.3 3.8 2.4 3.8 2.1 3.1
5
WIP
max
8 8 5 8 4 6
Table 5: The production cycle time of each allocation.
Allocation 1 2 3 4 5 6
Cycle time 155 155 116 116 116 116
Table 6: Cost coefficient value of each buffer.
Based on the computational results, the values of
functions
F
x
, F
y
and F
z
of each allocation are shown
in Table 7.
Table 7: The values of functions F
x
, F
y
and F
z
of each
allocation.
Allocation 1 2 3 4 5 6
(F
x
)
k
0.64 0.67 0.12 0.14 0.29 0.41
(F
y
)
k
15.6 15.6 0 0 0 0
(F
z
)
k
16.2 16.3 0.12 0.1 0.29 0.41
As seen in Table 7, the allocation 3 has resulted in
minimum
F
z
and therefore this layout is selected as
the optimum allocation of machines.
5 CONCLUSIONS
In this paper, the allocation of machines for doing
different operations in an automated assembling
shop has been discussed. The system features
identical multi-functional machines with different
processing times. A P-timed PN is applied for
modeling of the manufacturing system. The
proposed model is able to determine the average and
maximum WIP in different buffers as well as the
production cycle time associated with each
allocation pattern. The optimal layout is obtained
based on minimum WIP
average
and production cycle
time.
Buffer
1
2
3
4
5
C
j
0.08 0.1 0.16 0.21 0.05
ICEIS 2008 - International Conference on Enterprise Information Systems
522

REFERENCES
Adel, M., Baz, E.l., 2004. A genetic algorithm for facility
layout problems of different manufacturing
environments. Computers & Industrial Engineering,
(47)2-3, 233-246.
Alla, H., Ladet. P., Martinez, J., 1984. Silva SM.
Modeling and validation of complex systems by
colored Petri nets application to a flexible
manufacturing system. In: Rozenberg G, editor.
Advances in Petri Net, Lecture Notes in Computer
Science, Vol. 188. NY: Springer, 15–31.
Boubekri, N., Nagaraj, S., 1993. An integrated approach
for the selection and design of assembly systems.
Integrated Manuf Systems, 4(1), 11–7.
Cecil, J.A., Srihari, K., Emerson, C.R., 1992. A review of
Petri net applications in manufacturing. Int J Adv
Manuf Technol, 7,168–77.
Hsieh, Y.J., Chang, S. E., Chang, S.C., 2007. Design and
storage cycle time analysis for the automated storage
system with a conveyor and a rotary rack. Inter-
national Journal Production Research, January (2007).
Jehng, W.K., 2002. Petri net models applied to analyze
automatic sequential pressing system. Materials
Processing Technology, 120, 115-125.
Moore, K.E., Gupta, S.M., 1996. Petri net models of
flexible and automated manufacturing systems: a
survey. Int J Prod Res, 34(11), 3001–35.
Muro-Medrano, P.R., Joaquin, E., Jose, L.V., 1992. A
rule-Petri net integrated approach for modeling and
analysis of manufacturing systems, In: Gentina JC,
Tzafestas SG. Editors, Robotics and flexible
manufacturing systems, Amsterdam: Elsevier Science
Publishers (North-Holland), 349–58.
Park, E., Tilbury, D.M., Khargonekar, P.P., 2001. A
modeling and analysis methodology for modular logic
controllers of machining systems using Petri net, IEEE
Trans Robotics Automat, 5(2), 168–88.
Peterson, J.L., 1981. Petri Net Theory and the Modeling of
Systems. Prentice-hall, Englewood Cliffs, NJ.
Petri, C., 1962. Kommunikation Mit Automation. Thesis
(Ph.D), Dissertation University of Bonn, Bonn, West
Germany.
Ramchandani, C., 1974. Analysis of Asynchronous
Concurrent System by timed Petri nets, Doctoral
Dissertation, NIT, Cambridge, NA.
Rampersad, H.K., 1994. Integrated and simultaneous
design for robotic assembly. New York, Wiley.
Rampersad, H.K., 1995. A case studies in the design of
flexible assembly systems. Int J Flexible Manuf
Systems, 7(3), 255–86.
Yan, H.S., Wang, Z., Jiao, X.C., 2003. Modeling,
scheduling and simulation of product development
process by extended stochastic high-level evaluation
Petri nets. Robotics Comput Integr Manuf, 19, 329–42.
Zhang, W., Freiheit, T., Yang, H., 2005. Dynamic
scheduling in flexible assembly system based on
timed Petri nets model, Robotics and Computer-
Integrated Manufacturing, 550-558.
OPTIMAL LAYOUT SELECTION USING PETRI NET IN AN AUTOMATED ASSEMBLING SHOP
523
