
SOLVING THE UNIVERSITY COURSE TIMETABLING
PROBLEM BY HYPERCUBE FRAMEWORK FOR ACO
Jose Miguel Rubio L, Broderick Crawford L. and Franklin Johnson P.
Escuela de Ingenieria Informática, Pontificia Universidad Católica de Valparaíso, Valparaiso, Chile
Keywords: University Course Timetabling Problem, Ant Colony Optimization, Ant Systems.
Abstract: We present a resolution technique of the University Course Timetabling Problem (UCTP), this technique is
based in the implementation of Hypercube framework using the Max-Min Ant System. We show the
structure of the problem and the design of resolution using this framework. A simplification of the UCTP
problem is used, involving three types of hard restrictions and three types of soft restrictions. We solve
experimental instances and competition instances, the results are presented of comparative form to other
techniques. We present an appropriate construction graph and pheromone matrix representation. Finally the
conclusions are given.
1 INTRODUCTION
The Timetabling problems are faced periodically by
each school, college and university in the world. In a
basic problem, a set of events (particular classes,
conferences, classes, etc) must be assigned to a set
of hours of a way that all the students can attend all
of their respective events. With the reservation of
which restrictions of hard type which necessarily
they must be satisfied and soft restrictions exist that
deteriorate the quality of the generated schedule. Of
course, the difficulty of any particular case of the
UCTP (Cooper and Kingston, 1996) (ten Eikelder
and Willemen, 2001) depends on many factors and
in addition the assignment of rooms perceivably
makes the problem more difficult in general.
Many techniques have been used in the
resolution of this problem, among these we can find
evolutionary algorithms, simulated annealing, and
tabu-search. Other technique has presented good
results is the genetic algorithms (Burke, Newall and
Weare, 1996). But here specifically we represent the
resolution through the ant colony optimization
(ACO) and through the implementation of
Hypercube framework for Max-Min Ant System
(abbreviation in Spanish MTH-SHMM). We give a
representation for the problem, generating an
appropriate construction graph and the respective
pheromone matrix associated.
In the following sections we present the UCTP
problem, the problem design for Hypercube
framework, the instances of the problem used and
the results of the experimentation. Finally the
conclusions of the work.
2 UCTP DESCRIPTION
The problem timetabling considered to make this
study is similar to one presented initially by Paechter
in (Paechter, 2001). Timetabling of university
courses is a simplification of a typical problem
(Paechter, Rankin, Cumming and Fogarty, 1998). It
consists of a set of events E and must to be
scheduled in a set of timeslots T ={t
1
,…,t
k
} (k = 45,
they correspond to 5 days of 9 hours each), a set of
rooms R in which the events will have effect, a set
of students S who attend the events, and a set of
features F required by the events and satisfied by the
rooms. Each student attends a number of events and
each room has a maximum capacity. A feasible
timetable is one in which all the events have been
assigned a timeslot and a room so that the following
hard constraints are satisfied:
No student attends more than one event at the
same time;
The rooms must be big enough for all students
who attend a class and to satisfy all the
features required by the event;
Only one event is in each room at any
timeslot.
531
Miguel Rubio L J., Crawford L. B. and Johnson P. F. (2008).
SOLVING THE UNIVERSITY COURSE TIMETABLING PROBLEM BY HYPERCUBE FRAMEWORK FOR ACO.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 531-534
DOI: 10.5220/0001705505310534
Copyright
c
SciTePress
In short, All possible timetable generated is
penalized for each occurrence according to the
number of violations that exists of the soft constraint
of problem. Some of these restrictions appear next:
A student has a class in the last slot of the day;
A student has more than two classes in a row;
A student has exactly one class on a day.
Feasible solutions are always considered to be
superior to infeasible solutions, independently of the
numbers of soft constraint violations. In fact, in any
comparison, all infeasible solutions are to be
considered equally worthless. The objective is to
minimize the number of soft constraint violations in
a feasible solution.
3 DESIGN OF HYPERCUBE
FRAMEWORK SHMM FOR
TIMETABLING (MTH-SHMM)
3.1 Resolution Structure
Given the restrictions presented in the previous
section and the characteristics of problem, we can
now consider the option to design an effective
MTH-SHMM for the UCTP. We have to decide how
to transform the assignment problem (to assign
events to timeslots) into an optimal path problem
which the ants can solve (Blum, Dorigo, 2004). To
do this we must create an appropriate construction
graph for the ants to follow. We must then decide on
an appropriate pheromone matrix and heuristic
information to influence the paths that the ants will
take through the graph.
We present the principal elements used to
generate the UCTP solutions, presenting in Figure 1
these three elements.
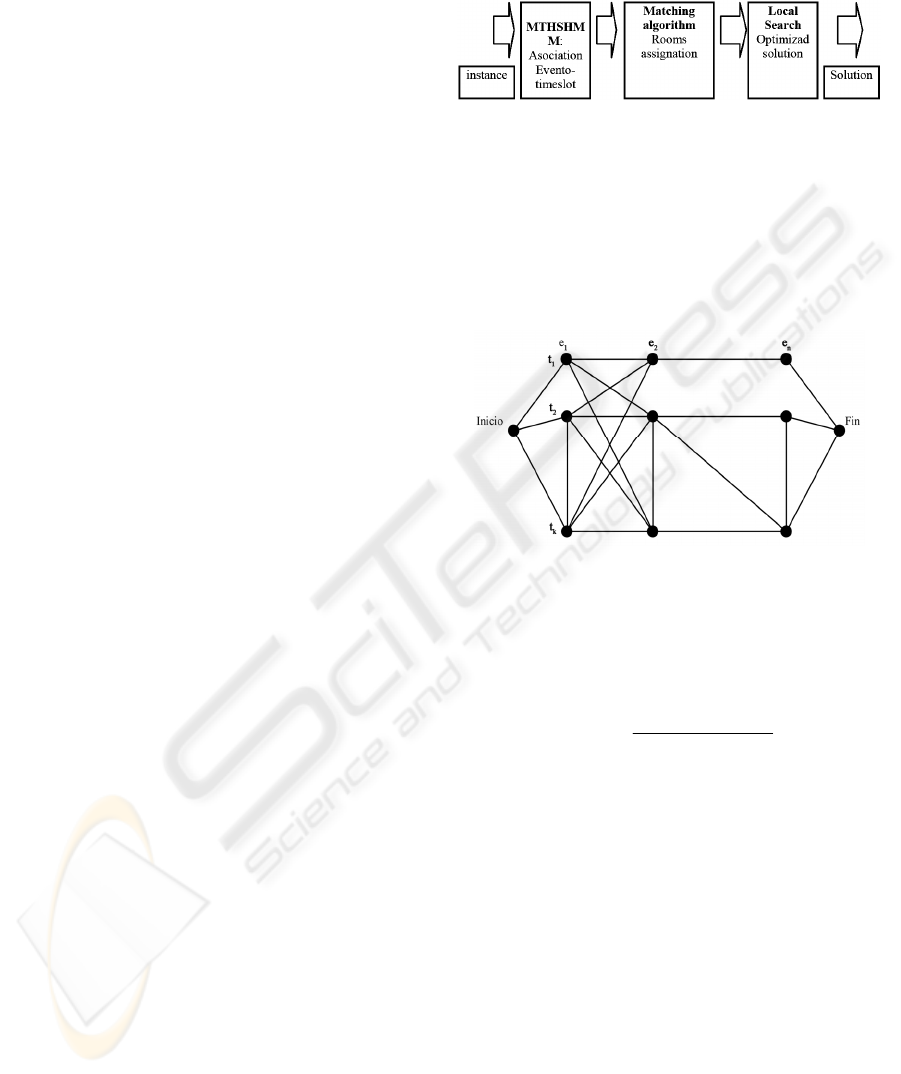
3.2 Construction Graph
One of the main elements of the ACO metaheurístic
is the power to model to the problem on construction
graph (Dorigo and Di Caro, 1999) (Blum, Dorigo
and Roli, 2001), that way a trajectory through the
graph represents a problem solution. In this
formulation of the UCTP it is required to assign each
one of │E│ events to │T│ timeslots. Where the
direct representation of the construction graph is
given by E × T; given this graph we can then
establish that the ants walk throughout a list of
events, choosing timeslot for each event. The ants
follow one list of events, and for each event and, the
ants decide timeslot t. each event at this single time
in timeslot, thus in each step an ant chooses any
possible transition as show the figure 2.
Figure 1: An instance of the problem is received like
input, this it happens through an association process event-
timeslot, assigns events to a timeslot, later a matching
algorithm ( Socha, 2003) is used for makes the assignation
from rooms to each one of events associated to timeslot. In
this point a solution is complete, but is low quality. Then a
local search algorithm (Rossi-Doria, Blue, Knowles and
Sampels, 2006) is applied that improves the quality of the
solution and gives like final result one optimal solution to
the UCTP.
Figure 2: Each ant follows a list of events, and for each
event e Є E, an ant chooses a timeslot t Є T.
The ants travel through the construction graph
selecting ways of probabilistically way. Using the
following function:
∑
∈
=
T
te
te
te
i
i
p
θ
α
α
θ
τ
τ
)(
)(
),(
),(
),(
(1)
3.3 The Pheromone Matrix
In search of a pheromone matrix we represented that
pheromones indicates the absolute position where
the events must be placed. With this representation
the pheromone matrix is given by τ (A
i
) = τ, i=1,…,
|E|, the pheromone does not depend on the partial
assignments A
i
. It can observe that in this case the
pheromone will be associated with nodes in the
construction graph rather than edges between the
nodes.
A disadvantage of this directs pheromone
representation is that the absolute position of events
in the timeslots it does not matter very much in
producing a good timetable. The relative placement
of events is more important. For example, given a
ICEIS 2008 - International Conference on Enterprise Information Systems
532

perfect timetable, it is usually possible to permute
many groups of timeslots without affecting the
quality of the timetable.
By other side, we defined that for the use of the
heuristic information η it must use a function that
calculates a weighted sum of several or all of the
soft and hard constrains in each assignation, which is
to incur very high computational cost stops this class
of problem (Socha, 2003). For this we will not use
this type of information to orient the route of the
ants.
4 EXPERIMENTATION
The framework is based in an algorithm in which
some modifications are made of presented in (Socha,
Knowles and Sampels, 2003) (Stützle and Hoos,
2000), it was implemented in C++ programming
language, under Linux system using GNU G++
compiler GCC 2.96. The behavior of Hypercube
framework Max-Min Ant System (MTH-MMAS)
was observed in the resolution of the UCTP. The
used instances appear below.
Instances 1: Instances of the UCTP are
structured using a generator described in
http://www.dcs.napier.ac.uk/~benp. This generator
allows generating classes of instances small,
medium, which reflect varied problems of
timetabling of several sizes.
Instances 2: In addition it was used a series of 20
instances created for International Timetabling
Competition, these instances are made with the same
generator used in instances 1.
The parameters study are made initially, to
evaluate the best values than must to assume these
parameters. The small (small1) instances was used
for using the MTH-MMAS without local search
making evaluations with different ants numbers m
and with different evaporations factors ρ, the
parameters of α = 1, number on attempts = 10 and a
maximum time by attempt = 90 seconds for all the
tests. The results are in the following table.
In the table it can observed the best results are
obtained using the parameter m=20 obtaining a
evaluation of 16 in 6.06 seconds. And for the case of
evaporation factor the best value is =0,5 in 8.1
seconds.
The values shown in the tables previously
presented they belong to a series of executions that
allow of experimental form to determine as are more
advisable parameters to use in the execution of the
algorithm of MTH-MMAS. This way we compared
the algorithm of the Max-Min Ant System with and
without Hypercube framework, in addition the local
search is included to increment the quality of the
solutions in different instances.
Table 1: It presents the best results obtained when proving
the instance small1.tim varying ants number m and
evaporation factor ρ.
Best solutions MTH-SHMM
m
Evaluation Tº seg.
ρ
Evaluation Tº seg.
5 17 6,79 0,2 15 7,11
10 16 7,46 0,5 13 8,1
20 16 6,06 0,8 17 6,79
4.1 Comparison with other Techniques
Here it present a comparative picture between the
solutions obtained for different instances for the
UCTP doing use of different techniques like
Simulated annealing, advanced search and simulated
annealing with local search. (Rossi-Doria, Blue,
Knowles and Sampels, 2006). The results obtained
for the competition instances appear below.
Table 2: It present the best results obtained when proving
the instances of the International Timetabling Competition
compared with other techniques.
Technique 1 2 3 4 5 6 7 8 9 10
SA 45 25 65 115 102 13 44 29 17 61
AS
257 112 266 441 299 209 99 194 175 308
SA-LS
211 128 213 408 312 169 281 214 164 222
MTH-
MMAS
270 193 294 586 406 221 305 244 201 358
Technique 11 12 13 14 15 16 17 18 19 20
SA
44 107 78 52 24 22 86 31 44 7
AS
273 242 364 156 95 171 148 117 414 113
SA-LS
196 282 315 345 185 185 409 153 281 106
MTH-MMAS
268 312 341 403 222 234 371 184 345 201
For these instances and compared with the
other solutions the MTH-MMAS it present two
characteristics to evaluate; first it has the capacity to
generate feasible solutions for these instances. These
instances are of great you make difficult since they
are for Timetabling competitions. Second the quality
of the generated solutions is of very low category
compared with the technique based on Simulated
Annealing, which has the best found historical
results for these instances, but in comparison with
the other instances do not present great difference.
These evaluations are not feasible in order to decide
if a technique is better than other, since the
differences in variable results can be for different
external variables.
SOLVING THE UNIVERSITY COURSE TIMETABLING PROBLEM BY HYPERCUBE FRAMEWORK FOR ACO
533

To continuation it presents the comparison for
the small and medium instances. We will compare
the algorithm of MTH-MMAS and the MMAS
pure with respect to Ant Colony System algorithm
of Krzysztof Socha (ACS) and to algorithm based on
random restart local search (RRLS).
As it is possible to observe, for these instances
in the MTH-MMAS present superiority in the
quality of the generated solutions (smaller VRS).
Always by on the quality the solutions generated
with the MMAS. We can say that the hypercube
framework it improves the quality of the ant
algorithm applied
Table 3: It present best results obtained when proving the
test instances small and medium.
Technique Small1 small2 small3 medium1 medium2
RRLS
11 8 11 199 202
ACS
1 3 1 195 184
MMAS
3 6 3 152 250
MTH-MMAS
0 4 1 138 186
5 CONCLUSIONS
A formal model was given to apply Hypercube
framework to solve the University course
timetabling problem (UCTP) making use of Max-
Min Ant System, was generated an efficient model
that solves instances of this problem creating good
construction graph of and expressing a good
pheromone matrix.
We presented the test result made for the Max-
Min Ant System making use of Hypercube
framework. We observed traverse of the given
results, that this propose framework is good means
of resolution of combinatorial problems and for the
case of the UCTP it presented good results for
instances of small and medium type. Although the
results were low quality for the instances of the
competition it emphasizes the fact that always it
generates solutions feasible and for instances of
normal difficulty of good evaluation, not obtain the
best results for this problem, but if it improves in
contrast with the Max-Min Ant System without
framework.
REFERENCES
T. B. Cooper and J. H. Kingston. The complexity of
timetable construction problems. In Proceedings of the
1st International Conference on Practice and Theory of
Automated Timetabling (PATAT 1995). 1996.
H. M. M. ten Eikelder and R. J. Willemen. Some
complexity aspects of secondary school timetabling
problems. In Proceedings of the 3rd International
Conference on Practice and Theory of Automated
Timetabling (PATAT 2000), 2001.
E. K. Burke, J. P. Newall, and R. F. Weare. A memetic
algorithm for university exam timetabling. In
Proceedings of the 1st International Conference on
Practice and Theory of Automated Timetabling
(PATAT 1995), 1996.
B. Paechter. Course timetabling. Evonet Summer School,
2001.
B. Paechter, R. C. Rankin, A. Cumming, and T. C.
Fogarty. Timetabling the classes of an entire
university with an evolutionary algorithm. (1998).
M. Dorigo and G. Di Caro. The Ant Colony Optimization
meta-heuristic. New Ideas in Optimization, 1999.
Christian Blum, Marco Dorigo, Andrea Roli, HC-ACO:
The Hyper-Cube Framework for Ant Colony
Optimization IEEE Transactions on Systems, Man
and Cybernetics B, 34(2), 1161 - 1172, 2001.
Krzysztof Socha, Max-Min Ant System for International
Timetabling Competition. (2003)
Krzysztof Socha, J. Knowles, y M. Sampels. Max-Min Ant
System for the University Course Timetabling
Problem.(2003)
http://www.dcs.napier.ac.uk/~benp
Thomas Stützle y H.H. Hoos, MAX-MIN Ant System.
Future Genetic Computing System. 2000.
Christian Blum, Marco Dorigo, The Hyper-Cube
Framework for Ant Colony. Optimization IEEE
Transactions on Systems, Man and Cybernetics B,
2004. HCF 2004.
Rossi-Doria, Blue, Knowles, Sampels, A local search for
timetabling problem.(2002)
ICEIS 2008 - International Conference on Enterprise Information Systems
534
