RELATING SYSTEM DYNAMICS AND

MULTIDIMENSIONAL DATA MODELS

A Metamodel based Language Mapping

Lars Burmester

Institute of Management Information Systems, Philipps-University Marburg

Universitaetsstrasse 24, Marburg, Germany

Matthias Goeken

Management Information Systems, Frankfurt School of Finance & Management

Sonnemannstrasse 9-11, Frankfurt (Main), Germany

Keywords: Metamodelling, Conceptual Modelling, System Dynamics, Multidimensional Modelling.

Abstract: System Dynamics (SD) is an approach with a long tradition used for modelling and simulation of complex

system. Early, a conceptual modelling language was applied to bridge the ‘linguistic gap’ between the natu-

ral language of the model users and the targeted simulation language. Despite the maturity of the modelling

approach, up to today no linguistic metamodel exists for the used language, resulting in non complying lan-

guage extensions and the lack of reasonable combination with other modelling languages, e.g. for use in

Business Intelligence (BI) systems. This paper aims at the development of a linguistic metamodel of the SD

modelling language. Further, by relating the elaborated SD metamodel with multidimensional data model-

ling, an approach for positioning SD in a modern BI context is shown.

1 INTRODUCTION

System Dynamics (SD) is a modelling approach

with a long tradition, reaching back to the beginning

of the 1960s (Forrester, 1964). Here, diagram lan-

guages were applied early to bridge the ‘linguistic

gap’ between the natural language of the model

users and the targeted simulation model language

(consisting of a set of differential equations).

Despite the maturity of this modelling approach,

up to today linguistic definition (linguistic meta-

model) exists for the used language. The conse-

quence is mainly twofold. At first, extensions to the

language which do not comply the rules of the defi-

nition could cause consistency problems in its appli-

cation. Secondly, the reasonable combination with

other modelling languages, e.g. for use in decision

support systems, is limited. Though, being widely

used for business planning issues SD lacks proper

integration into modern Business Intelligence (BI)

context. For example, though SD models are explic-

itly time variant, they are seldomly related to data

warehouse or OLAP concepts, although these are

time variant as well (Inmon, 2005).

This paper aims at the development of a linguis-

tic definition of the language used in SD modelling

in terms of a linguistic metamodel. Further, the

elaborated metamodel should be related to multidi-

mensional data modelling, to enhance the applica-

bility of SD in modern BI context. Note, that this

paper focuses solely on the conceptual properties of

the SD modelling language for reasons of brevity.

Hence, implementational and calculational aspects

remain – as far as possible – unconsidered.

The paper proceeds as follows. In section 2, the

SD metamodel is developed by introducing the main

concepts of the language, as well as their combina-

tion rules, followed by the specification of the

metamodel. In the following 3rd section, the SD

metamodel is related to multidimensional data mod-

elling. The paper closes with conclusions and pro-

jected further research opportunities.

295

Burmester L. and Goeken M. (2008).

RELATING SYSTEM DYNAMICS AND MULTIDIMENSIONAL DATA MODELS - A Metamodel based Language Mapping.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - ISAS, pages 295-299

DOI: 10.5220/0001707802950299

 SciTePress

2 SD METAMODEL

SD is an approach for modelling and simulation of

complex and dynamic (socio economical) systems.

Characteristic for SD is the emphasis on closed

cause and effect chains between system elements

which often lead to a counterintuitive behaviour of

the system (Forrester, 1969, p. 107 ff.). Through

simulation of the models, this counterintuitive be-

haviour can be revealed and taken into account for

possible decisions.

This section begins with an introduction to the

language concepts of the level/rate language. As

mentioned above, only the conceptual aspects of the

language should be considered, calculational and

implementational aspects must stand back. All ex-

planations refer to the type level of the language

which leads to a structural description of a model.

The following rationale refers to textual descrip-

tions of the level/rate language found in (Forrester,

1964, pp. 68-83; Forrester, 1972, pp. 140-145; Rob-

erts, 1981, pp. 19-20; Sterman, 2000, pp. 192-204.

2.1 Constructs

2.1.1 Node Types

Levels are containers, representing state values of

system elements. The value of a level changes over

time, being the accumulated difference between

inflows and outflows of content into, respectively

out of the level.

Rates control the flow between the levels of a

system, representing the activity inside a system.

The control of a flow is achieved via decision func-

tions which determine the amount of flow depending

on information about levels in the system.

Auxiliary variables do not belong to the original

concepts of the level/rate language. From a calcula-

tional point of view, auxiliary variables are equation

parts, unhinged from (comprehensive) rate equa-

tions. From a conceptual point of view, they are

informational concepts, having an independent

meaning. They influence the decision functions that

control the rates and are themselves influenced by

levels and / or other auxiliaries and constants (see

below). In sum, they are derivative concepts, intro-

duced for pragmatic reasons, for easing the commu-

nication and improving the clarity of the model.

Sources and sinks represent the boundaries of a

system model. Sources are the stocks from which a

flow coming from outside the model originates.

Respectively, sinks are the stocks taking flows

which leave the model.

Constants are state variables which do not or change

that slowly that they could be assumed constant for

the time scope of the model.

2.1.2 Edge Types

Flows are the edges connecting levels, representing

the inflow and outflow altering the level. Inflows are

pointing at the level, adding content to the level,

outflows are pointing away from the level, subtract-

ing content from the level.

Information links are immaterial and connect the

inputs for the decision function of a rate. Infor-

mation links may point to rates and auxiliary vari-

ables, but not to levels (may only be changed by

flows, see above), constants (do not change, see

above) and sources or sinks (beyond scope, see

above). However, information links may point away

from all element types (information take-off), except

sources or sinks (again: beyond scope).

2.2 Metamodel

The following section presents the metamodel of the

level/rate language. The reading order is from node

type to edge type. Additionally, the naming conven-

tion of the relationship types indicates the direction

of the edges, e.g. ‘Level precedes Flow’ describes a

flow edge, pointing away from a level node. A dia-

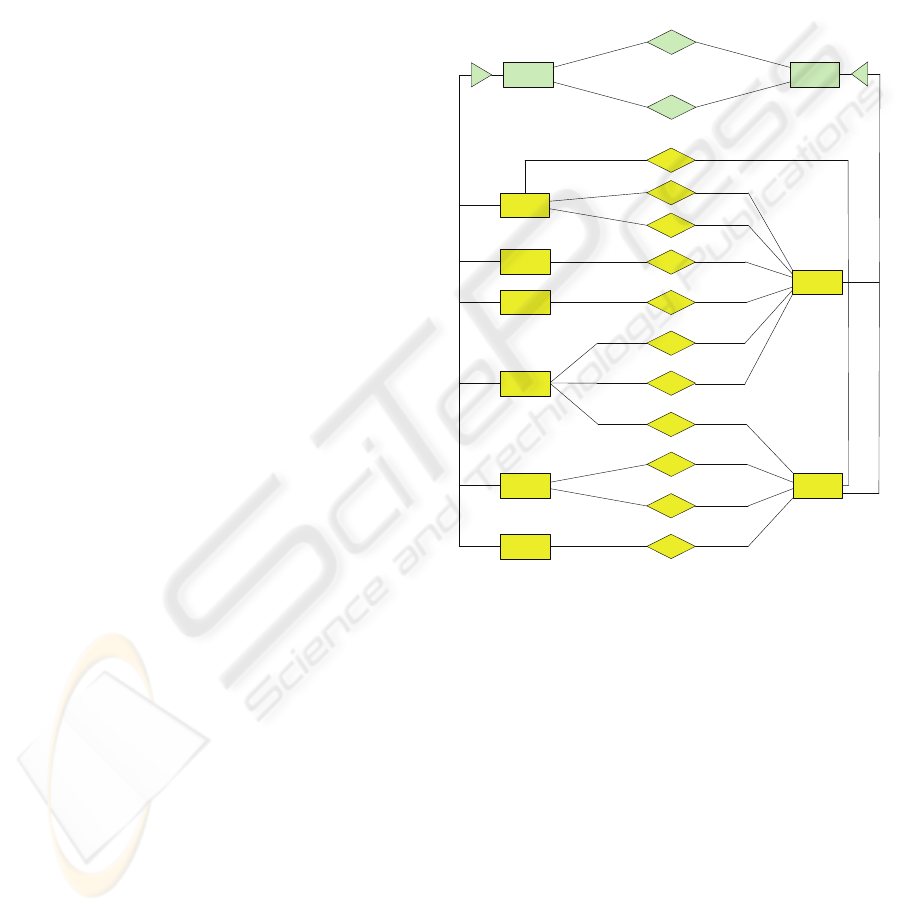
gram of the resulting metamodel is shown in Figure

Levels.

(1) Levels are connected to flows pointing at or

pointing away from the level. This relationship can

be represented as a level succeeding or preceding a

flow.

(2) Forrester states that ‘A level may have any

number of inflows and outflows’, (Forrester, 1964,

p. 68, Footnote 2) which results in cardinalities of

(0, 1) on the level side and (0, m) on the flow side.

(3) It is declared that a level can only be changed

by flows. In particular no causal link can point di-

rectly into a stock. However, it is possible that a

causal link can point away from a stock (stock pre-

cedes causal link; see below).

Rates.

(1) It is stated that rates define the flows between

the levels of a system. Provided that node types

cannot directly connect to other node types, an edge

type has to be the intermediate. Here, the flow type

is the intermediate between a rate and a level. Be-

cause a flow is controlled by exactly one rate, the

cardinalities are (1, 1) on both sides (rate and flow).

ICEIS 2008 - International Conference on Enterprise Information Systems

296

(2) Rates are determined by the levels of a sys-

tem. Additionally, rates underlie influences of other,

not yet specified concepts (see below).

Auxiliaries.

(1) From a calculational point of view, auxilia-

ries are parts of the decision functions of a rate.

They can be embedded (substituted) into the equa-

tions underlying the rates. From a conceptual point

of view, auxiliaries have an independent meaning.

They represent certain aspects of a rates decision

function that, for reasons of clarity, should be pre-

sented separately from the rates.

(2) Auxiliary variables are related to levels,

rates, constants and other auxiliaries. They connect

to these other constructs solely via information links.

Auxiliary variables are depending on levels, con-

stants and other auxiliaries which means that an

information link points from the related concept

towards the auxiliary (auxiliary succeeds informa-

tion link). The concepts influencing an auxiliary

precede an information link ({level | constant |

(other) auxiliary} precede information link precedes

auxiliary). As stated above, auxiliaries are part of

rates decision functions, directly or indirectly influ-

encing the rate of flow. A direct influence would be

modelled as an information link pointing towards the

rate (rate succeeds information link), an indirect

influence would be modelled as an information link

pointing towards another auxiliary (auxiliary pre-

cedes information link succeeds auxiliary).

The cardinalities of the listed relationships are as

follows:

- A constant (0, 1) precedes one to many

(1, m) information links.

- A level (0, 1) precedes zero to many (0, m)

information links.

- An auxiliary variable (0, 1) precedes one to

many (1, m) information links.

- An auxiliary variable (0, 1) succeeds zero

to many (0, m) information links.

- A rate (0, 1) succeeds one to many (0, m)

information links.

Constants. Constants influence rates directly or

indirectly via auxiliary variables, connecting to them

through information links (constant precedes

information link precedes {auxiliary | rate}).

Constants themselves do not change which means no

other concept influences (precedes) them. The

cardinalities for this relationship would be (0, 1) on

the constant side and (1, m) on the information link

side.

Sources and Sinks. Sources are stocks generating

flows from outside the models boundaries. Sinks are

stocks taking flows outside the models boundaries.

These facts could be modelled as source preceding a

flow, respectively a sink succeeding a flow. Since

the sources and sinks are not differentiated regarding

their contents, the cardinalities would be (0, 1) on

source and sink side and one to many (1, m) on the

flow side.

Figure 1 shows the abstract syntax of the

level/rate language. The node types and edge types

could be generalised into a more compact represen-

tation of the metamodel (see upper part of Figure 1).

Node-type

Edge-type

Precedes

Succeeds

d, t

Rate

Level

Precedes

Succeeds

0, 1

0, m

0, 1

0, m

Precedes

Succeeds

1, 1 1, 1

1, 1

Auxiliary

Information

Link

Precedes

Succeeds

0, 1

1, m

0, 1

0, m

Succeeds

0, 1

0, m

Constant

Precedes

0, 1 1, m

Sink

Source

Flow

Precedes

Succeeds

1, m

0, 1

Precedes

0, 1

0, m

Figure 1: Abstract syntax of the level/rate language.

3 SD MODELS IN OLAP

CONTEXT

In the following, the SD metamodel will be used for

positioning SD models in a modern BI context.

Core elements of state of the art BI solutions are

data warehouse systems, storing relevant data in

support of management decisions, and OLAP sys-

tems which process this data to multidimensional

information (Burmester & Goeken, 2006). Though,

there are some similarities between these systems

and SD models, little work is found relating these

concepts to one another. Golfarelli et al. propose the

use of SD models for conducting what-if analysis

and representing the results in OLAP context. How-

ever, the lack of semi-formal languages for specify-

RELATING SYSTEM DYNAMICS AND MULTIDIMENSIONAL DATA MODELS - A Metamodel based Language

Mapping

297

ing the requirements is pointed out as a research

issue (Golfarelli et al., 2006, S. 54). In the following,

a linguistic approach for relating SD and multidi-

mensional modelling is introduced.

To relate multidimensional and SD modelling,

the core constructs of the former should be briefly

introduced. Multidimensional data models consist of

quantifying and qualifying information concepts.

The quantifying concept, often referred to as meas-

ure, represents values of selected business objects

(e.g. turnover, sales etc.). Measures are qualified

through dimensions, describing them from selected

points of view (e.g. time, region, customer) leading

to concrete information (e.g. sales for December

2007 (time) in Germany (region) at ‘Mega Mart’

(customer)). Dimensions consist of nodes (in the

following called dimensional nodes) which are

regularly organised to hierarchies. The hierarchisa-

tion allows changing the level of detail a business

object is represented, adapting view complexity to

the actual information requirements. The multidi-

mensional approach, accompanied by the described

complexity adaption mechanism through hierarchi-

sation, allows users to visualise a comprehensive

picture of business objects.

For relating the approaches, the quantifying and

qualifying aspects of SD models must be identified.

However, this requires an extension of the scope of

considerations from solely static aspects of model

structure towards the dynamic results yielded by a

simulation of the model. During the simulation of

the model, the values of the variables are calculated,

depending on their interrelationships while the

simulation time advances. The result is a time series

for each variable representing the value of a variable

at a certain point of time. A model could be simu-

lated with different parameterisation, meaning that

the value of constants and initial values of variables

differ between two simulation runs. The result is

another set of time series which could be compared

to time series from previous simulation runs.

The sets of time series could already be regarded

as multidimensional information about the SD

model. The quantifying information within a model

are the variables changing during the simulation.

The values of these variables are obviously qualified

by a time dimension. Furthermore, the variables of a

SD model depend on a set of parameters defined at

the beginning of a simulation. These parameters also

qualify the values of the variables generated during

simulation, with each parameter constituting a di-

mension. The variation of a model parameter be-

tween simulation runs leads to a set of dimensional

nodes which should be hierarchised into a dimen-

sional hierarchy.

In terms of the metamodel the above described

could be formulated as follows. The node types

mentioned in section 2.1.1 can be specialised into

parameters of the model (qualifying information)

and variables (quantifying information). The pa-

rameters of a model are the constants and the initial

values of the variables. The variables of the model

are the levels, rates and auxiliary variables. Other

node type concepts (sinks, sources) remain uncon-

sidered because they cannot assume values.

The constructs of multidimensional models are

dimensional nodes, dimensions and measures. Di-

mensional nodes are part of a dimension which de-

scribes measures. The relationship between quanti-

fying measures and qualifying dimensions could be

reinterpreted as an OLAP Cube.

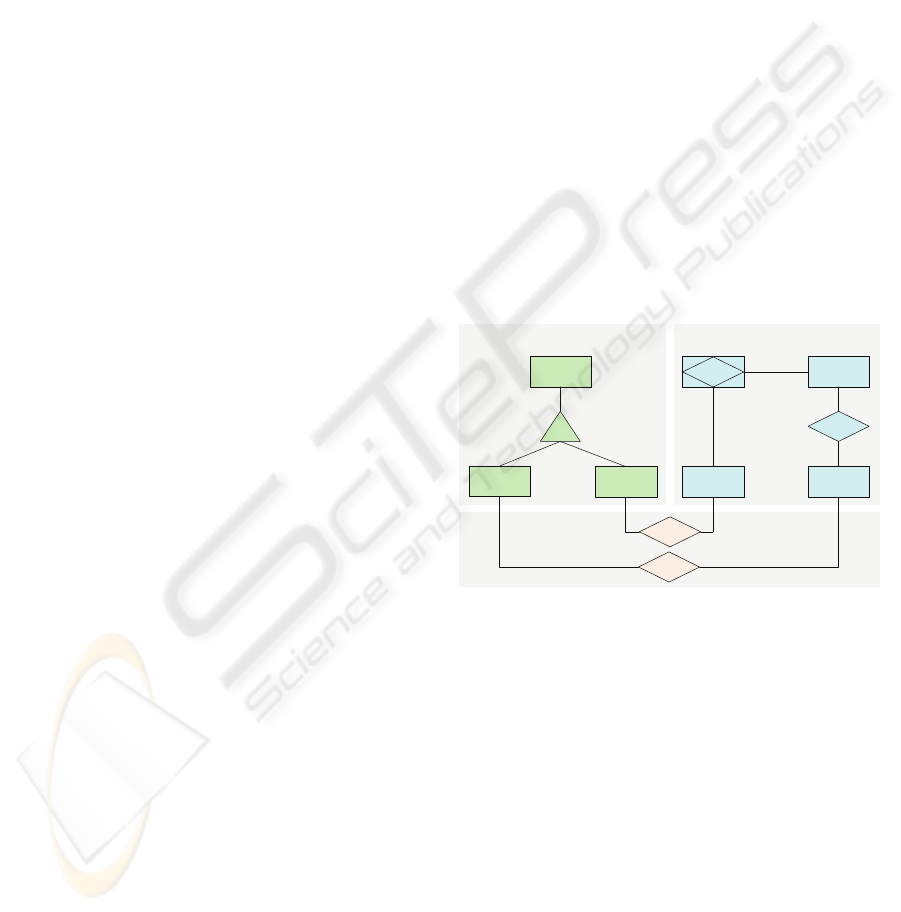
The resulting models and their correspondences

are depicted in figure 2. As stated above, parameters

of the SD model correspond to dimensional nodes

and variables of the SD model correspond to meas-

ures (diagrammed as dotted lines).

Multidimensional ModelingSystem Dynamics

Node-type

Parameter

Variable

d, t

Measure

OLAP Cube

Dimensional

Node

Dimension

part of

maps to

Figure 2: Mapping the SD metamodel to multidimensional

modelling.

4 CONCLUSIONS AND

PROJECTED NEED OF

FURTHER RESEARCH

In this paper we presented a metamodel of the SD

modelling language and showed a way of repre-

senting the simulation results in a multidimensional

manner. The combination of information enriching

multidimensionality and complexity reducing hier-

archisation can be considered state of the art for the

support of managerial work. The complementation

of this approach with a possibility to simulate com-

ICEIS 2008 - International Conference on Enterprise Information Systems

298

plex, dynamic and often counterintuitive system

behaviour augments management support.

Further research based on our findings could be

directed into three directions. From the viewpoint of

decision science it could be evaluated how far the

augmented information improve the quality of

managerial decisions.

From a practical point of view, the explanation

of a modelling language is not sufficient for practi-

cal applicability of the introduced ideas. Further

research should be pointed at introducing a way of

working with the language definitions and be aimed

towards a methodology (see also Golfarelli et al.,

2006 for a similar statement of research issues).

From a linguistic-theoretical point of view, an

ontological analysis of the modelling language and

the representational benefits of its extension could

be interesting (Wand & Weber, 1993, Rosemann &

Green, 2002)). During this analysis, the ontological

completeness (according to a reference ontology,

e.g. Bunge-Wand-Weber or Chisholm) would be

examined for the original language as well as for the

result of an extension. Further, hints for combination

of the level/rate language with other modelling lan-

guages to reduce the representational deficiencies

could be produced.

REFERENCES

Burmester, L., Goeken, M., 2006. Method for User

Oriented Modelling of Data Warehouse Systems. In Y.

Manolopoulos, J. Filipe, P. Constantopoulos & J.

Cordeiro (Eds.), Proceedings of the 8th International

Conference on Enterprise Information Systems,

Volume III.

Forrester, J., 1964. Industrial Dynamics. Cambridge,

Mass.: MIT Press, 4

edition.

Forrester, J., 1969. Urban dynamics. Cambridge, Mass.:

MIT Press.

Forrester, J., 1972. Grundsätze einer Systemtheorie:

(Principles of systems). Wiesbaden: Gabler.

Golfarelli, M., Rizzi, S., Proli, A., 2006. Designing What-

if Analysis: Towards a Methodology. In I. Song & P.

Vassiliadis (Eds.), Proceedings of the 9th

International Workshop on Data Warehousing and

OLAP (DOLAP 06) (pp. 51–58). New York: ACM.

Inmon, W. H., 2005. Building the data warehouse.

Indianapolis, Ind.: Wiley.

Roberts, E. B. 1981. System Dynamics - An Introduction.

In E. B. Roberts (Ed.), Managerial applications of

system dynamics (pp. 3–35). Cambridge, Mass.: MIT

Press.

Rosemann, M., & Green, P. 2002. Developing a meta

model for the Bunge-Wand-Weber ontological

constructs. Information Systems, 27(2), 75–91.

Sterman, J. D. 2000. Business dynamics: Systems thinking

and modeling for a complex world. Boston:

Irwin/McGraw-Hill.

Wand, Y., & Weber, R. 1993. On the ontological

expressiveness of information systems analysis and

design grammar. Journal of Information Systems, 7(3),

217–237.

RELATING SYSTEM DYNAMICS AND MULTIDIMENSIONAL DATA MODELS - A Metamodel based Language

Mapping

299