
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS
Rosa Matias
1
, João-Paulo Moura
2, 4
, Paulo Martins
2, 4
and Fátima Rodrigues
3, 4
1
Polytechnic Institute of Leiria, Morro do Lena - Alto Vieiro, Leiria, Portugal
2
Department of Engineer, University Of Trás-os-Montes e Alto Douro, Vila Real, Portugal
3
Department of Informatics, Porto Institute of Engineering, Porto, Portugal
4
Knowledge Engineering and Decision Support Research Center, 4200-072 Porto, Portugal
Keywords: Visual Data Mining, Spatial Clustering, Information Visualization.
Abstract: It is stated that a closer intervention of experts in knowledge discovery can complement and improve the
effectiveness of results. Normally, in data mining, automated methods display final results through
visualization methods. A more active intervention of experts on automated methods can bring enhancements
to the analysis; No meanwhile that approach raises questions about what is a relevant stopping stage. In this
work, efforts are made to couple automatic methods with visualization methods in the context of
partitioning algorithms applied to spatial data. A data mining workflow is presented with the following
concepts: data mining transaction, data mining save point and data mining snapshot. Moreover to display
results, novel visual metaphors are changed allowing a better exploration of clustering. In knowledge
discovery, experts validate final results; certainly it would be appropriate to them validate intermediate
results, avoiding, for instance, losing time, when in disagreement, starting it with new hypnoses or allow
data reduction by disable an intermediate cluster from the next stage.
1 INTRODUCTION
A geospatial dataset (in Geographic Information
Systems (GIS) a layer) is compounded by semantic
and spatial attributes and emulates the design of
some kind of phenomena that occurs in the surface
of the earth. An organization can collect many
geospatial datasets all large in volume and high-
dimensionality. Many factors contribute to the
accumulation of spatial data in organizations. For
instance, the mobility of people increases the
development of Location Based Applications that
monitors people and goods. Organizations always
have collected information with a geographic
component, for instance: addresses, phone numbers
and events (where did something happen). Also
disciplines related to earth sciences have a strong
spatial component.
The unprecedented large size and dimensionality
of existing datasets make the complex patterns that
potentially lurk in data hard to find (Guo, Peuquet,
& Gahegan, 2003). Spatial data has a complex and
specific nature bringing particular issues to the
discovery of hidden patterns – extracting knowledge
from spatial datasets is a multivariable, multilayer
and multi data type problem. No meanwhile, the
spatiality can enrich the analysis by bringing graphic
elements (like thematic maps).
There are three main approaches to extract
knowledge from geospatial datasets (Demsar, 2006):
(i) spatial data mining. Invent new spatially aware
data mining algorithms; (ii) spatial pre-processing.
Model spatial properties and relationships in pre-
processing followed by the application a common
data mining algorithm; and (iii) exploratory geo-
visualization. Apply visual data mining to spatial
data allowing the analyst, by visualization, to
interact directly, identify patterns, and draw
conclusions.
In this work the last approach is used. A
partitioning algorithm is chanced in order to display
intermediate results so that experts can interact more
deeply with the automatic method.
Only experts can interpret and validate the
results produced by clustering. The high
dimensionality and volume of datasets makes it
difficult to find the right clusters. Frequently, results
are in disagreement with specialists’ intuition (Guo,
78
Matias R., Moura J., Martins P. and Rodrigues F. (2008).
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 78-86
DOI: 10.5220/0001709400780086
Copyright
c
SciTePress

Gahegan, MacEachren, & Zhou, 2005) and (Nam,
Han, Mueller, Zelenyuk, & Imre, 2007).
The involvement of users (experts) in
intermediate stages allowing then to understand the
flow of the automatic process can bring interesting
results to the analysis, since, experts have a more
comprehensive view about attribute values and
attribute combination. In their knowledge domain
they are the better agents to explore attribute
combination. Moreover, different experts can have
different interests in the analysis. They can
formulate new hypotheses after exploring attributes
or attribute values, focus on one know pattern and
continue the process in order to make some
conclusions.
In this paper a semi-automatic approach to
cluster spatial data is presented. A partitioning
algorithm is monitored. Through visualization
experts can make conclusions observing both spatial
and non-spatial results produced in intermediate
stages of execution. They can, for instance, conclude
that a cluster has already been found. Because, in
knowledge discovery, results have the expert
validation, in this kind of system experts should also
validate, previous, intermediate results.
For instance, the expert detects that objects, of a
cluster, have similar geographic location and
confirms some logic in attribute combination. Then
he considers that a cluster has been found. In this
scenario, the implicated objects can be removed,
making the next stage, of the automatic method,
lighter.
Displaying intermediate results has a main
problem: when and how the automatic method
should be stopped. Moreover users should have an
interactive interface to allow a convenient
exploration of attribute combination (discovering
relevant values for cluster formation).
This paper pretends to answer the following
questions: (i) What is the workflow of semi-
automatic process?; (ii) What is a stopping
condition?; (iii) How to display and allow the
exploration of intermediate results produced by
spatial clusters?. This paper is organized as follow:
the next section makes an overview of spatial
clustering algorithms, visual data mining and related
work. In section 3 we propose an interaction model
for visual and spatial clustering. In section 4, as
prove of concepts a case of study is presented.
Finally we make some conclusions and point out
future work.
2 BACKGROUND CONCEPTS
In this work, our automation method, is a medoid
algorithm, namely, PAM (Partitioning around
Medoids) (Kaufman & Rousseeuw, 1990). It makes
an exhaustive search in order to produce effective
results. Commonly medoid algorithms are applied in
problems that process distances between geospatial
entities. For instance, discover the most central
points of a metropolitan region; discover the best
location for water pumps, in a city, with thousands
of buildings, (being the water pumps considerer the
medoids).
Visual data mining combines concepts from data
mining and information visualization, and integrates
algorithms with graphic elements enabling data
display and user interaction.
There are a large discrepancy between computers
and humans. Computers can automatically process
large amounts of data faster than humans but are
incapable of interpreting results. On the other hand
humans are able to interpret visual results
recognizing patterns more efficiently then computers
(Demsar, 2006), (Nam, Han, Mueller, Zelenyuk, &
Imre, 2007) and (Keim, 2002). The process of
clustering could be improved if both automated and
visual capabilities were more deeply integrated
enabling an additional active participation of experts
in the knowledge discovery process.
Next we make a closer look at PAM. Later we
make an overview of visual data mining. Finally, we
identify related work of relevance.
2.1 K-medoids Algorithms applied to
Spatial Data
Partitioning methods reallocate iteratively objects to
clusters in order to gradually improve the quality of
the final result. The more known partitioning
methods are: k-means, k-medoids and fuzzy
clustering. k-means and k-medoids find disjoint
clusters; in fuzzy clustering all objects have some
probability of belonging to all clusters. k-means and
k-medoids algorithms differ in their central object –
the first uses a gravitational point, the later a
representative object (medoid).
The most know k-medoids algorithms are:
Partition Around Medoids (PAM) (Kaufman &
Rousseeuw, 1990), Clustering Large Applications
(CLARA) (Kaufman & Rousseeuw, 1990) and
Clustering Large Applications Based in Randomized
Search (CLARANS) (Ng & Han, Efficient and
Effective Clustering Methods for Spatial Data
Mining, 1994).
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS
79

In PAM: First a proximity matrix is computed
storing the distance between all pairs of objects.
Normally the distance is the Euclidian and expresses
absolute differences in values of dimensions.
Second a first group of medoids are randomly
chosen. Third the distance of all objects to all
medoids is computed (cost matrix) and objects
(called non medoids) are associated to the closest
medoid. Fourth verify for each medoid if there is a
non medoid that produces a better cluster. If so, a
permutation must be done (non medoid is promoted
to medoid and the medoid passes to non medoid). A
new cost matrix is computed and non medoids are
reallocated again. The process continues until
permutations no longer exits.
Because of the exhaustive search PAM is
considered effective and efficient for small datasets.
To overcome PAM efficient problems CLARA and
CLARANS have been proposed. In CLARA, PAM
is applied to samples extracted from a dataset.
CLARANS is compared to a search in a graph where
each node represents a group of medoids; two nodes
are neighbors if they differ in one medoid and a
jump between two nodes is persecuted if a neighbor
of a node produces better clusters. CLARANS is
considered better than CLARA because the
randomize search is applied to all dataset being
independent of the quality of samples.
In partitioning methods, attributes are projected
in space and objects are represented in a plane by
points. Their distance mirrors their similarity. The
adaptation of traditional partitioning algorithms to
spatial data is trivial since spatial data is commonly
represented by points and distance is one of the most
important spatial relationships. Even though
particular changes in algorithms have happen
because of the spatial data types (beyond points
there are lines and polygons); and spatial
relationships (beyond distance there are direction or
topology). For instance particular algorithms
addresses: (i) spatial object heterogeneity.
Computing distances between points, lines and
polygons needs particular attention. Polygons have
irregular shape and occupy a region. The similarity
function can’t be computed using the Euclidian
distance and the irregularity of polygons has
computational costs. In (Ng & Han, CLARANS: A
Method for Clustering Objects for Spatial Data
Mining, 2002) three ways for computing polygons
distances are compared. They conclude that the best
way is to compute distances between polygons using
the closest points between polygons approximations
(ii) obstructions. When computing distances
between two spatial objects, others spatial objects
can obstruct the way, for example, two buildings can
be separated by a river being their distance
dependent on the location of the bridge. In (Wang &
Hamilton, 2005) and (Tung, Hou, & Han, 2001)
changes are made in PAM, CLARA and CLARANS
for dealing with obstruction; and (iii) roads and
paths. In the surface of the earth, human’s
movements are made using roads so, distances
between two spatial objects can be a function of the
distance within roads (Ibrahim, 2005).
2.2 Visual Data Mining: Architectures,
Visual Tools and Issues
Large datasets cause serious problems for
visualization techniques and these problems can be
divided in two groups (Guo, Gahegan, MacEachren,
& Zhou, 2005): (i) computational efficiency
problem (time needed to process the data); and (ii)
visual effectiveness problem (display of large
datasets makes patterns hard to find and perceive).
Software architectures that integrate visualization
in data mining can be classified as (Ankerst, 2000):
(i) visualization of final results. Helps interpret
results allowing their comparison and verification.
An algorithm extracts patterns from the data and
patterns are displayed for human observation. Based
on the interpretation, the user may want to return to
the data mining algorithm and run it again with
different input parameters (figure 1.a); (ii)
visualization of intermediate results. An algorithm
performs an analysis of the data but at some
intermediate step results graphically displayed. Then
the user retrieves interesting patterns and make
decisions about the next step (figure 1.b); and (iii)
visualization of data. Data is visualized
immediately without running a sophisticated
algorithm before. Users explore the dataset and can,
for instance, reduce data or attributes that are used as
input for algorithms (figure 1.c).
Visual data mining can bring greet enhacements
to the analysis, no meanwhile it is a challenge task,
since a multidimensional space has to be displayed
in a 2D screen. Furthermore human visual system
can´t process system simultaneously a large number
of graphic elements. Example of information
visualization techniques are scatter plots, histograms
and bar graphics.
ICEIS 2008 - International Conference on Enterprise Information Systems
80
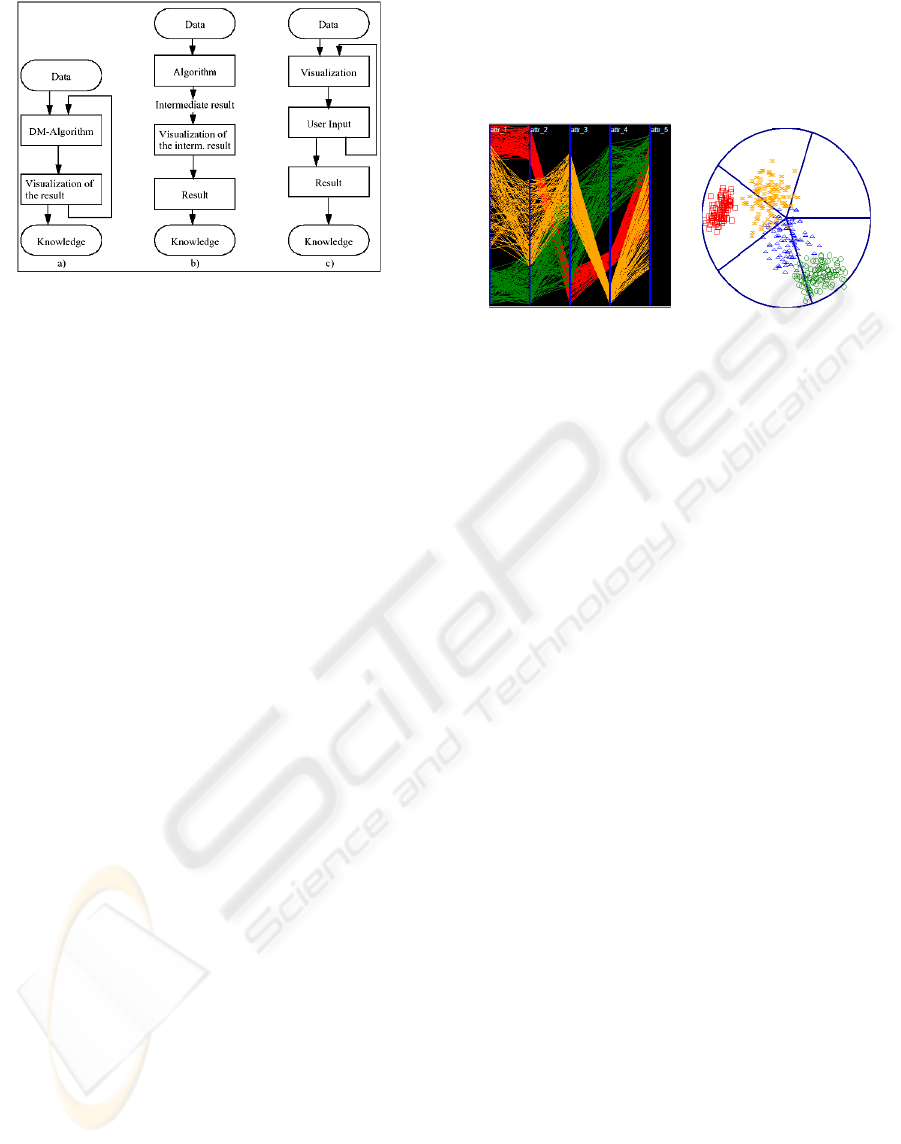
Figure 1: Architectures for Visual Data Mining.
Novel information visualization techniques have
been defined allowing a better exploration analysis
of large and multidimensional data sets. Most know
techniques are (Kantardzic, 2003): (i) Geometric
projection techniques. Projections for
multidimensional datasets; normally concerned with
the display of multidimensional spaces in a 2D
plane; (ii) Icon-based techniques. Display small
icons to represent attribute values; (iii) Pixel-
oriented techniques. Each object in the dataset is
represented by a pixel; and (iv) Hierarchical
techniques and graph. Information is displayed like
in a graph or hierarchy. Works like (keim 2002)
make an overview of these tecnhiques and tools.
Next we describe some visualization tools
related to this work. They are: (i) Parallel
Coordinate Plots (PCP) (Inselberg, 1985). The
objective is to represent a multivariable dataset in a
2D plane (like a screen of a computer). A backdrop
is drawn consisting of n equally spaced parallel lines
each one representing a dimension (figure 2.a)). For
each object a polyline is drawn and the position of
the vertex on the i-th axis corresponds to the i-th
coordinate of the object;
(ii) Radial Visualization (Hoffman, 1999). Its
goals are similar of PCP but the plane is represented
by a circle with axes equally spaced. The number of
axes is equall to the number of dimenions. An object
makes a physical strength in the i-th axe similar to
the i-th coordinate and a representative point is
drawn where the sum of all forces is zero (figure
2.b)). This tool enables an analysis of the efforts
made by dimensions. It is also a way to visually
display the structure or geometry of clusters; (iii)
Self Organized Maps (SOM) (Kohonen, 1990)
produces low dimension representation of training
samples while preserving the topological properties
of the input space. Useful to visualize, in a low
dimensional space, high dimensional data. It consists
in two steps. First a traning stage is made to build
the map with samples. Then a mapping stage is
performed to classify the input data. Each object is
represented by a vector with values from
dimensions. The object is associated to the cell with
the most similar vector
a)Parallel Coordinate Plot b) Radial Visualization
Figure 2: Example of geometric techniques.
2.3 Related Work
In (Nam, Han, Mueller, Zelenyuk, & Imre, 2007) a
visual tool, called cluster sculptor, is presented for
exploring large and high dimensional datasets. The
clustering engine implements a k-means algorithm.
Users are allowed to tune parameters interactively,
like: geometry, composition and spatial relations.
Their environment has tools for visually explore
hierarchical classifications by means of an
interactive dendrograma (operations like zoom,
merge and moving object between clusters).
In (Guo, Gahegan, MacEachren, & Zhou, 2005)
an integration of computational, visual and
cartographic methods is studied in order to visualize
multivariable spatial patterns. SOM is coupled with
a colour scheme to summarize a large amount of
data. Other novel visual data mining tool is PCP:
used to help interpreting multivariable patterns.
In (Demsar, 2006) investigates if combining
automated and visual data mining is suitable
approach for exploring geospatial data. The work
proves that novel visual elements, like snowflake
graphs, and SOM can be integrated with automatic
data mining algorithms like helping experts
investigate geodatasets.
In (Guo, Chen, MacEachren, & Liao, 2006)
present a novel geo-visual analytical strategy for
exploring and understanding spatial-temporal and
multivariable patterns. They also develop a
methodology to cluster, sort, and visualize large
datasets with spatial data allowing experts to
investigate large and complex patterns in spatial and
temporal dimensions.
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS
81

3 A MODEL FOR VISUAL AND
SPATIAL CLUSTERING
As already stated, in a spatial cluster there are
objects with both semantic and spatial attributes; it
means, that clustering can be applied in
miscellaneous approaches. We propose the
following approaches, to get spatial clusters: (i) non-
spatial oriented. Apply the algorithm only to
semantic attributes. The spatial attribute is displayed
in a thematic map (spatial object, of the same
cluster, are drawn with the same color). This
spatiality of clusters enables the identification of
regions with similar behaviors. Inside a spatial
cluster, objects can be near, spread all over the space
or have some pattern correlated with some
relationship with another geographic phenomenon;
(ii) spatial and semantic oriented. Apply
algorithms both to semantic and spatial attributes
(separately). A thematic map is generated with two
different iconographic elements: one for semantic
patterns and other with a spatial pattern; (iii) spatial
oriented. Apply the algorithm to the spatial
attribute. For instance, identify the most central
entities of a layer (e.g., in a large area, where are
urban centres?); and (iv) multi-spatial oriented.
Apply algorithms to different layers tracking spatial
relationships, like topology, distance and directions.
This approach avoids pre-processing relations
between layers, making it possible to parameterize
spatial relations on-the-fly.
In this work, we use the non-spatial oriented
approach, and implement a visual data mining
architecture based on the visualization of
intermediate results (as presented in figure 1.b). .
In the context, of intermediate results
visualization, we formulate the following questions:
What is a stopping condition? How to handle more
than one stopping condition? When visualization
should be persecuted? What visual elements should
be used? Which actions should be allowed?.
We make the following considerations: First
experts are responsible for specifying relevant stop
condition, since they have more experience and
intuition about datasets; Second there must be some
flexible but controlled form to specify those
stopping stages, protecting the automatic process
against meaningless setting; Third in algorithms an
unit of work should be enclosed, to watch and check
his state; Fourth, since there are a large numbers of
dimensions and objects users can configure many
stopping condition.
Next we make some definitions about concepts
for a spatial and visual data mining system. We call
the visual data mining workflow.
3.1 Visual Data Mining Workflow
In a semi-automated method a visual data mining
workflow is a group of visual data mining
transactions (one for every stop condition). A save
point detect a stop condition whose state can be
displayed through a visual snapshot. Next we make a
detail explanation of those concepts.
Definition 1. Unit of work. In medoid oriented
algorithms, a step is a unit of work that ends with
clustering (group of clusters) and has a timestamp.
The clustering state is measured computing: (i)
inter-cluster and intra-cluster similarities, for
instance, the number of objects, min, max and
average distance, distance between medoids,
cohesion and separation; (ii) is_link_pattern.
Intermediate patterns about values in dimensions
considerer relevant.
Definition 2. Visual save point. Happen when a
clustering has a state in agreement with a stop
condition, parameterized by experts. The automatic
method stops and gives rise to the visual method,
expressing the status of the current clustering.
Definition 3. Visual and spatial snapshot.
Graphic elements that express the state of a visual
save point and enables some level of interaction.
Definition 4. Visual data mining transaction. A
relevant condition. In the context of a visual data
mining workflow experts can configure many visual
data mining transactions (conditions). No meanwhile
the can be none or many save points.
Figure 3 shows the concepts associated to the
visual data mining workflow. The automated method
is coupled with the visual method.
Figure 3: Visual Data Mining Workflow.
How to stop the automatic method? We propose
three main parameterizations: (i) Using ‘must link’.
Subdivide into: Stop using semantic states – some
combination of values in a sub group of attributes;
ICEIS 2008 - International Conference on Enterprise Information Systems
82

Stop using spatial states – geographic objects can
have specific relationships with other geographic
layers. For instance, in urban crime experts can
declare that violent crimes happen near old buildings
(the system looks to the relationship, in each cluster,
between the location of crimes and old buildings);
(ii) stop with periodicity. Use a regular step
interval; and (iii) stop using similarities between
steps. Verify if a constant metric is present between
clustering (from step to step) – if so maybe a cluster
has already been found.
Figure 4 presents a diagram showing the
interaction between automated and visual methods.
Figure 4: Stopping the process.
3.2 Exploring Clusters
An abstraction of a cluster is made using an ellipse,
whose size, colour and position are in agreement
with properties of clusters. A thematic map is
generated by cluster (each cluster has a different
colour). If the dataset is large, instead of displaying
geographic objects, a geometric approximation can
be computed, for each cluster, allowing a more
suitable observation.
The visual elements for exploring clusters are: (i)
Cluster Abstraction. A group of ellipses represents
a group of clusters; (ii) Interactive PCP.
Understand the data distribution inside and between
clusters; and (iii) Interactive RV. Understand data
distribution and structure inside and between
clusters.
The interaction model has synchronized
granularity managed and controlled by a central
component (controls the parameterization of colours
and the display of clusters and attributes).
3.2.1 Visual Abstraction of Clusters
The ellipse is rendered on screen on a position
computed by the spring model stated in section 2.2.
The spring model enables the computation of central
points in screen using values of medoids. Figure 5a)
shows an ellipse where the number of axes is equal
to the number of attributes (four). In each axe the
strength is equal to the attribute value. Figure 5b)
shows the equilibrium point (central point).
Figure 5: Computing the screen central point of a cluster
using the medoid.
In equation 1, α represents an angle, β is the
angle step and
α
d is the value made, at α, by a
dimension d.
3.2.2 Interactive PCP
PCP is a component that projects the spectrum of
clusters through dimensions translating an n
dimension space in a 2D space. Using a colour
scheme is possible to distinguish clusters from each
other. By observing the map and the PCP users have
a legend for interpreting the projection of
dimensions in the map (Guo, Gahegan, MacEachren
& Zhou (2005)). No meanwhile, more can be done.
In this work, interactive exploration is improved by
allowing: (i) attribute reorder. The expert sets
relevant attributes side by side in order to compare
them and conclude, for instance, that in a cluster the
combination of some attribute values are correct; (ii)
attribute zooming. The expert makes a closer look
at some detail in a dimension in order to better
understand how values spread over the dimension. If
all clusters have a similar value in a dimension then
users can conclude that the dimension doesn’t have a
strong influence in the identification of clusters and
so can be removed in a subsequent step; (iii)
attribute hide. Similar to reorder but dimension
disappear from the component; (iv) cluster cut.
Turning clusters visible or invisible allowing a better
observation of one or some clusters; and (v)
attribute move. Automatic had-doc position
ordering by exchanging plane positions allowing the
observation of all possible combinations in
dimensions; (vi) store the picture. In a black box
execution, the current projection of clusters in PCP,
can be stored as an image in disk enabling a future
analysis; (vii) values cut. Using the mouse users can
draw a rectangle in order to watch, in the PCP, only
objects whose values are inside some selected area
excluding values that are not interesting; change
⎪
⎪
⎩
⎪
⎪
⎨
⎧
×=
×=
⇔=
∑
∑
∑
+=
+=
=
º360
º360
1
)(
)cos(
0
βαα
α
βαα
α
αω
αω
ω
dseny
dx
F
n
i
i
(1)
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS
83
layout. Experts can make a new thematic
parameterization of clusters changing colors, size of
lines.
3.2.3 Interactive RV
Interactive RV also projects an n dimensional space
in a 2D space. In this case, dimensions are axes of an
ellipse making it possible to observe the
combination of strengths made by dimensions
(higher or lower values). It uses colors and icons to
render clusters.
This component has the same operations with the
same meaning retracted in Interactive PVP, namely:
(i) attribute reorder; (ii) attribute zooming; (iii)
attribute hide; (iv) cluster cut; (v) attribute move;
(vi) store the picture; and (vii) values cut; (vii)
change the layout.
The image produced by this component makes it
possible to analyze the spatial structure of clusters in
a 2D space. Tracking intermediate stages by storing
images produced by this component enables a dipper
comprehension about how clusters are formed along
the time.
All actions in RV also have impact in the map and
the PCP. Also in the map an operation (topology,
distance, and direction) restricts the data that is
displayed in others components.
4 CASE OF STUDY:
ANALYSING AN URBAN
INFRASTRUCTURE
In order to identify the benefits of the described
concepts, a scenario related to an urban drainage
infrastructure, implemented in small urban areas, is
used for experiments. Users are allowed to identify
correlations inside a spatial cluster and between
spatial clusters. The approach is non-spatial
oriented. The spatial dataset has a geographic
attribute representing pieces of the network having
each the following semantic attributes:
Year: (<1975, [1980-1985], 1[987-1994], >1994).
Status: A classification of the actual situation of a
chunk (active, proposed, future).
Station: A classification of the type of station for
residual water treatment (ETAR, FOSSA)
Material: (Material, Class). A classification of
material used to build the network (GRES, PVC,
PVCC).
The algorithm PAM was changed stopping at
configured save points and displaying intermediate
results. The dataset has 400 objects and 4
dimensions. Results for four clusters are presented.
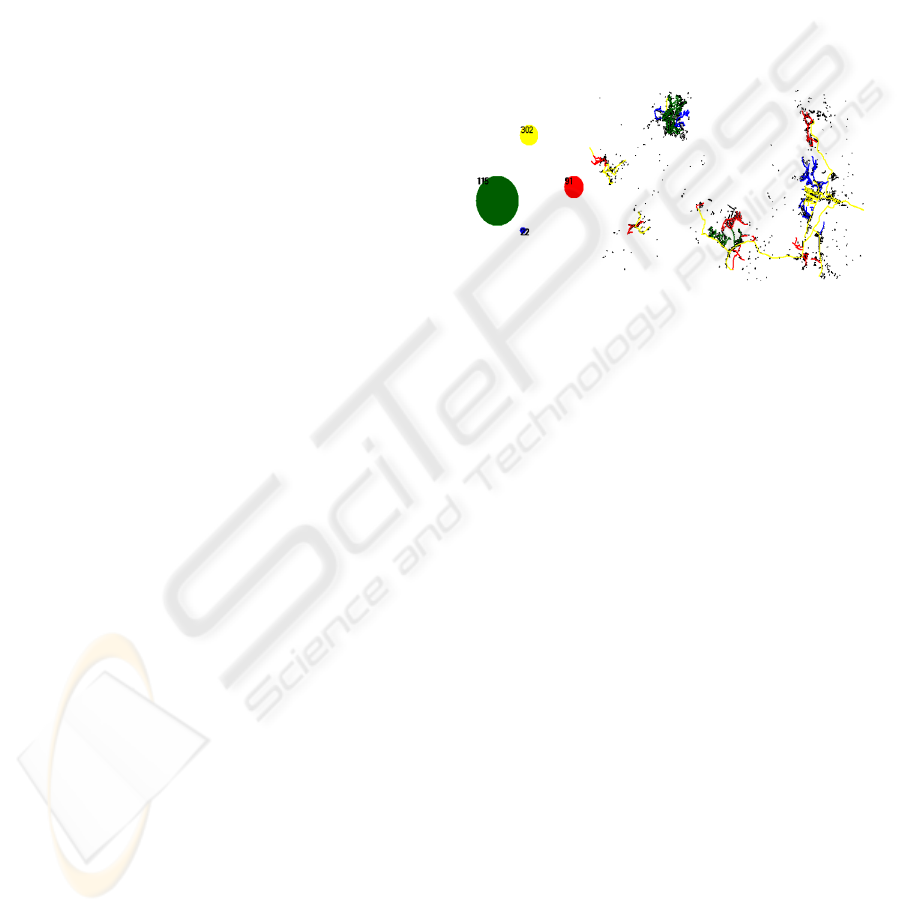
Figure 6 shows an image with spatial clusters
obtained after the application of the automatic
method. The size of ellipses expresses the amount of
objects allocated to clusters. In thematic maps, the
color used to paint a geographic object identifies his
cluster. In the ellipse a label identifies her medoid.
Figure 6: Visualization of spatial clusters.
The green cluster (115) is the largest, being their
spatial component concentrate in two areas; after
overlapping the map with a layer of buildings, it can
be pointed out that geographic objects are
concentrated in the middle of urban areas. The red
cluster (91) is located at non-dense regions (rural
regions). The yellow (302) cluster is associated to
the highest networks (the ones that are connecting
small rural regions). Finally, the blue cluster (91)
takes place in low concentrated regions.
After this visual interpretation, a closer look to
semantic attributes can be persecuted allowing the
interpretation of the semantic and spatial
correlations.
In figure 7 the interactive PCP and interactive RV
are displaying attributes and dimensions to users;
through a set of checkboxes is possible to execute on
the fly combinations of clusters with dimensions.
The image figure 7.a) shows that objects have very
similar values at adjacent dimensions like
tmanutencao and tmaterial since lines that connect
them are overlapped (yellow lines belong to the last
rendered cluster). This can have two meaning: (i)
dimensions do not contribute to cluster formation; or
(ii) small differences can be a factor to a cluster
formation if the others dimensions are more similar.
ICEIS 2008 - International Conference on Enterprise Information Systems
84
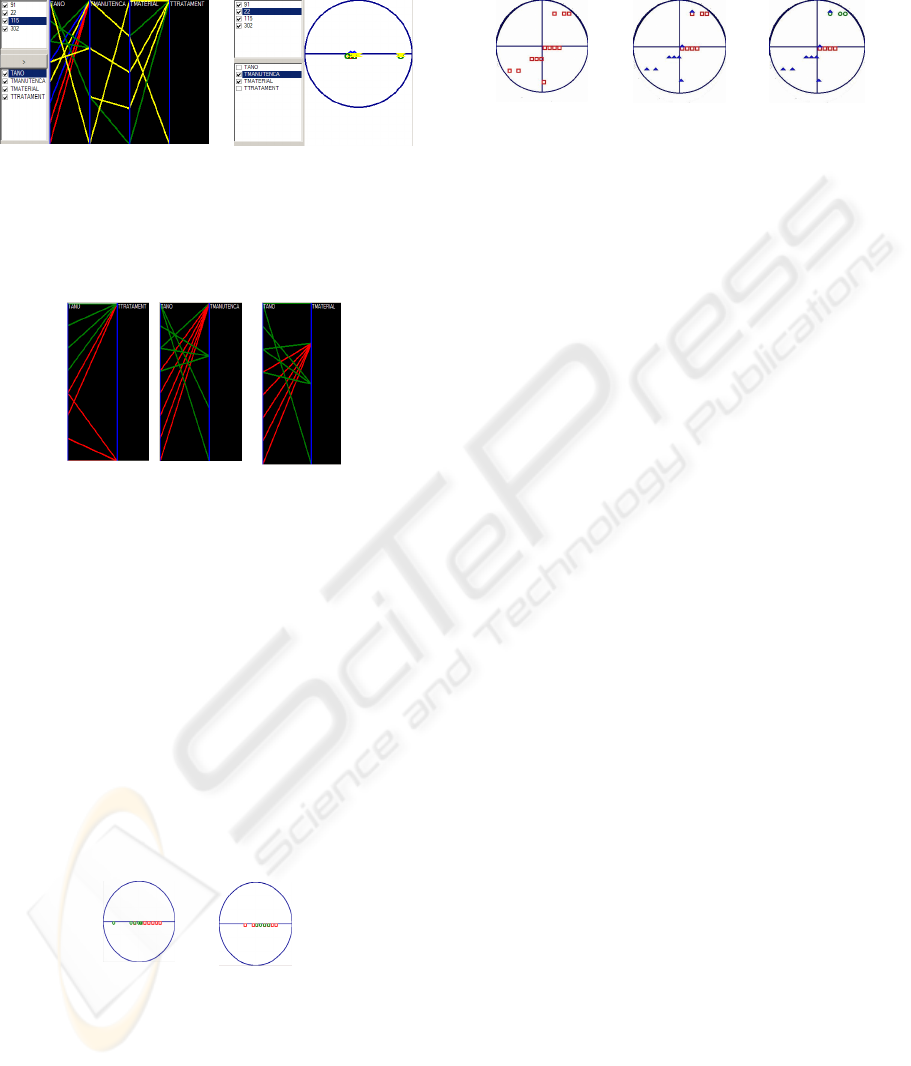
In figure7.b) RV confirms object similarity in the
two dimensions by showing that the distribution of
objects along those two dimensions is concentrated.
Figure 7: Interactive PCP and Interactive RV.
In figure 8 sample images of interactive PCP are
presented.
a) b)
c)
Figure 8: Visual combining of attributes.
The user performs a cluster cut selecting only the
two largest clusters (green and red), in order to
comprehend then. Then it performs attribute hide
in order to analyze the behaviour of the dimension
labeled tano. It can be pointed that the two clusters
have more similarities between labeled dimensions
tano and ttratamento (figure 8.a)).
Users can be confused about which pair of attributes
are more similar: (tano, tmanutencao) or (tano,
tmaterial). Using RV with only those dimensions
users can, for instance, conclude that the pair
(tano,tmaterial) is more dissimilar than (tano,
ttratamento) since, in the first pair, objects are
more spread over dimensions (figure 9).
a)
b)
Figure 9: Using the interactive RV to visually discover
similarities in dimension.
Figure 10 shows images about visual save points
related to a visual data mining transaction. It is
possible to observe the evolution of the clustering
process along the time and make some conclusions.
For instance, between save points 2 and 3 the
structure of a cluster (blue triangles) is maintained
which can mean that a cluster match has been
reached.
a) SavePoint 1
b) SavePoint 2
c) SavePoint 3
Figure 10: The evolution of a clustering process displayed
in RV and stored in disk.
In a large dataset, the process could be improved if a
prior cluster is found. Users are allowed to stop the
current automatic method and start it with a lower
number of objects, by eliminating the ones that
belongs to a validated cluster (data reduction) or
eliminating dimensions that do not make a strong
contribution to cluster discovery (dimension
reduction).
In a large dataset, experts can stop the current
automatic method and start it with a lower number
of objects, eliminating the ones that belong to valid
clusters already discovery.
5 CONCLUSIONS AND FUTURE
WORK
In this work a visual data mining system is presented
allowing some degree of interaction with
intermediate stages of automatic methods. The
concept of spatial data mining transaction is defined
has a group of visual save points that are in
agreement with a user stop condition. In a visual
save point a visual snapshot is generated showing
result of intermediate steps. In it experts can
conclude that a cluster as been found by exploring
attribute values combination. For that visual data
mining tools like PCP and RV are implement with
new operations allowing better attribute exploration
(like reorder, zooming, hide). Future work will be
done at the automatic method level by trying to
improve the interaction with clustering enabling a
more suitable way of attribute and data reduction.
REFERENCES
Ankerst, M. (2000). Visual Data Mining (PhD Thesis).
Munich: Institute of Computer Science, University of
Munich.
a) Interactive PCP (all
dimensions and attributes)
b) Interactive RV (only
some dimensions)
SEMI-AUTOMATIC PARTITIONING BY VISUAL SNAPSHOPTS
85

Demsar, U. (2006). Data Mining of Geospatial Data:
Combining Visual and Automatic Methods.
Stockholm: Royal Institute of Technology (KTH).
desJardins, M., MacGlashan, J., & Ferraioli, J. (2007 ).
Interactive Visual Clustering. Proceedings of the 12th
international conference on Intelligent user interfaces
(pp. 361 - 364 ). Honolulu, Hawaii, USA : ACM Press
Gahegan, M., & Brodaric, B. (2002). Computational and
Visual Support for Geographical Knowledge
Construction: Filling in the gaps between exploration
and explanation. Advances in Spatial Data Handling,
Proceedings of the 10th International Symposium on
Spatial Data Handling.
Guo, D., Chen, J., MacEachren, A. M., & Liao, K. (2006).
A Visual Inquiry System for Space-Time and
Multivariable Patterns (VIS-STAMP). Transactions on
Visualization and Computer Graphics , 12 (6), 1461-
1474.
Guo, D., Gahegan, M., MacEachren, A. M., & Zhou, B.
(2005). Multivariate Analysis and Geovisualization
with Integrated Geographic Knowledge Discovery
Approach. Cartography and Geographic Information
Science , 32 (2), 113-132.
Guo, D., Peuquet, D. J., & Gahegan, M. (2003). ICEAGE:
Interactive Clustering and Exploration of Large and
High-Dimensional Geodata. GeoInformatica (pp. 229-
253). The Nertherlands: Kluwer Academic Publishers.
Hoffman, P. (1999). Table Visualization: A Formal Model
and Its Applications (PhD Thesis). Lowell LA, USA:
University of Massachusetts Lowell.
Ibrahim, L. F. (2005). Using Clustering Algorithm CWSP-
PAM for Rural Network Planning. Third International
Conference on Information Technology and
Applications (ICITA'05) (pp. 280-283). Sydney: IEEE
Computer Society.
Imrich, P., Mueller, K., Mugno, R., Imre, D., Zelenyuk,
A., & Zhu, W. (2002). interactive Poster:Visual Data
Mining with the Interactive Dendogram. Information
Visualization Symposium.
Inselberg, A. (1985). The plane with parallel coordinates.
Visual Computer , 1 (4), 69-81.
Jiang, B. (2004). Spatial Clustering for Mining Knowledge
in Support of Generalization Process in GIS. ICA
Workshop on Generalisation and Multiple
Representation. Leicester, United Kingdom.
Kaufman, L., & Rousseeuw, P. (1990). Finding Groups in
Data: An Introduction to Cluster Analysis. John Wiley
& Sons.
Kantardzic, M. (2003). Data Mining: Concepts, Models,
Methods, and Algorithms. Danvers, MA, USA: John
Wiley & Sons.
Keim, D. A. (2002). Information Visualization and Visual
Data Mining. IEEE Transactions on Visualization and
Computer Graphics , 100-1007.
Kriegel, H.-P., Kunath, P., Pfeifle, M., & Renz, M. (2006).
ViEWNet: Visual Exploration of Region-Wide Traffic
Networks. Data Engineering, 2006. ICDE '06.
Proceedings of the 22nd International Conference on
(pp. 166-166). Atlanta, USA: IEEE Computer Society.
Koua, E. L., MacEachren, A., & Kraak, M.-J. (2006).
Evaluting the usability of visualization methods in an
exploratory geovisualization environment.
International Journal of Geographical Information
Science , 20 (4), 425-448.
Liu, W., Seto, K. C., & Sun, Z. (2005). Urbanization
Prediction with ART-MMAP Neural Network Based
Spatial-Temporal Data Mining Method. 5th
International Symposium Remote Sensing of Urban
Area (URS 2005), XXXVI. Tempe, AZ, USA.
May, M., & Savinov, A. (2004). SPIN! AN ENTERPRISE
ARCHITECTURE FOR DATA MINING AND
VISUAL ANALYSIS OF SPATIAL DATA. In B.
Kovalerchuk, & J. Schwing, Visual and Spatial
Analysis (pp. 293-317). Dordrecht, The Nertherlands:
Springer.
Nam, E. J., Han, Y., Mueller, K., Zelenyuk, A., & Imre, D.
(2007). ClusterScultor: A Visual analytics Tool for
High-Dimensional Data. IEEE Symposium on Visual
Analytics Science and Technology 2007 . Sacramento,
CA.
Ng, R. T., & Han, J. (2002). CLARANS: A Method for
Clustering Objects for Spatial Data Mining. IEEE
Transaction on Knowledge and Data Enginnering , 14
(5), 1003-1016.
Ng, R. T., & Han, J. (1994). Efficient and Effective
Clustering Methods for Spatial Data Mining. 20th
VLDB Conference. Santiago, Chile.
Schulz, H.-J., Nocke, T., & Schumann, H. (2006). A
Framework of Visual Data Mining of Structures. 29th
Australasian Computer Science Conference (pp. 157-
166). Hobart, Australia: Australian Computer Society,
Inc.
Tung, A. K., Hou, J., & Han, J. (2001). Spatial Clustering
in the Presence of Obstacles. 17th International
Conference on Data Engineering (ICDE'01).
washington, DC, USA: IEEE Computer Society.
Torun, A., & Duzgun, S. (2006). Using Spatial Data
Mining Techniques to Reveal Vulnerability of People
and Places Due to Oil Transportation and Accidents: A
Case Study of Istanbul Strait. Proceedings of the
ISPRS Vienna 2006 Symposium, (pp. 43-48). Vienna.
Wan, L.-H., Li, Y.-J., Liu, W.-Y., & Zhang, D.-Y. (2005).
Application and Study of Spatial Cluster and
Customer Partitioning. Fourth International
Conference on Machine Learning and Cybernetics (pp.
1701-1706). Guangzhou: IEEE.
Wang, X., & Hamilton, H. (2005). Clustering Spatial Data
in the Presence of Obstacles. International Journal on
Artificial Intelligence , 14, 177-198.
Zhang, X., Wang, J., & Wu, F. (2006). Spatial Clustering
with Obstacles Constraints Based on Genetic
Algorithms and K-Medoid. IJCSNS International
Journal of Computer Science and Network Security , 6
(10), 109-114.
ICEIS 2008 - International Conference on Enterprise Information Systems
86
