A PARTIAL-VIEW COOPERATION FRAMEWORK BASED ON THE
SOCIOLOGY OF ORGANIZED ACTION
Carmen Lucia Ruybal dos Santos
IEAV/CTA, S. J. Campos, SP, Brazil
Sandra Sandri
IIIA/CSIC, Bellaterra, Spain
Christophe Sibertin-Blanc
IRIT, Universit
´
e Toulouse 1, Toulouse, France
Keywords:
Organization, cooperation, sociology.
Abstract:
In this work, we address the extension of the modeling of a fragment of the Sociology of Organized Action,
making it possible to deal with a hierarchy of resources in an organization, allowing each of its members to
have his own view of the organization.
1 INTRODUCTION
In this paper we are interested in social games, in-
spired by a sociology theory called the Sociology
of Organized Action (SOA). This theory, initiated in
(Crozier, 1964), parts from the notion of bounded ra-
tionality due to March and Simon (Simon, 1996) and
extracts practical consequences from it (Crozier and
Friedberg, 1995).
SOA addresses social organizations or, more gen-
erally, Systems of Concrete Actions (SCA), that inter-
act with an environment, pursue some goals, and in-
clude some means, resources and tools, that are man-
aged and used by the members of the organization ac-
cording to some rules. Any such organization features
regulation phenomena that ensure its relative stability
and the balance of social relationships. This regula-
tion is enacted by the organization members, and SOA
intends to explain how and why social actors behave
as they do.
SOA assumes that each actor behaves strategically
although he has only bounded rationality capabilities.
According to SOA, the behaviour of a member of
an organization is fully explained neither by the for-
mal rules and norms of the organization, nor by each
member individual particularities resulting from his
nature and life history. Social actors have a strategic
behaviour, i.e., they perform actions with the inten-
tion to achieve some goals, and each actor aims, as
a meta-objective, at having enough power to preserve
or increase the autonomy and capacity of action he
needs in order to achieve his own goals.
The power of an actor results from, and is exerted
through, the mastering of uncertainty zones (UZ),
which are the resources that are needed by other ac-
tors for their actions. The actor (or group of actors) in
control of an uncertainty zone sets its exchange rules,
that establish how well other actors can access and
use this particular resource. UZs are thus the means
through which the power relationships are established
among social actors, and a balance results from the
fact that each actor both controls some UZs and de-
pends on some others.
SOA was formalized in (Sibertin-Blanc et al.,
2006), and is employed in the interactive environment
SocLab (available at sourceforge.net), which allows
the user to edit the structure of a SCA, to analyze
the properties of this structure and to simulate the be-
haviour of the social actors (Mailliard et al., 2003).
This formalization was transposed to the fuzzy set-
ting in (Sandri and Sibertin-Blanc, 2007a).
In this paper, we extend the original formalization
of SOA given in (Sibertin-Blanc et al., 2006) by mak-
ing it possible to assemble the resources of an orga-
nization in a hierarchy, so that we may consider re-
sources that are the synthesis of lower levels ones. In
553
Lucia Ruybal dos Santos C., Sandri S. and Sibertin-Blanc C. (2008).
A PARTIAL-VIEW COOPERATION FRAMEWORK BASED ON THE SOCIOLOGY OF ORGANIZED ACTION.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 553-558
DOI: 10.5220/0001711705530558
Copyright
c
 SciTePress

this way, each member of the organization may have
his own representation of the resources that are the
basis of his relationships with others. This makes it
possible to describe how a resource impacts the au-
tonomy of an actor in a more general way.
2 FORMALIZATION OF A
FRAGMENT OF SOA
In the following, we briefly describe the basic social
game formalization, as given in (Sibertin-Blanc et al.,
2006).
Within an organization, the actors are the active
entities that process the inputs and produce the out-
put and, by doing so, adapt their behaviours to the
behaviour of the other actors. On the other hand, the
resources (the UZs in SOA) are the means necessary
for the actors to properly behave and to reach not only
their own goals but also those of the organization. In
this formalization, every resource is mastered by a
single actor and every actor is assumed to master at
least one resource.
The state property of a resource characterizes how
this resource is managed by its controller, usually
rather to his own advantage or to that of a few cho-
sen actors. The characterization of how important a
resource is to an actor is done by allowing each actor
to distribute a limited amount of stakes among the re-
sources in the game. The amount of stakes an actor
puts on a resource is determined by how intensely he
needs this resource to reach his goals, in other words,
he puts more stakes on the resources he depends most.
When an actor depends on a resource, the effect
function determines the impact of the actual state of
the resource on his action capability. As a result, each
actor both controls some others, by means of the re-
sources he controls, and depends on others, by the re-
sources he needs. The overall state of an organiza-
tion is characterized by the composition of the states
of the resources it contains, and this characterizes the
behaviour of each actor with regard to others.
Let R be a set of resources, let stake(a,r) denote
the amount of stakes an actor a puts on resource r and
let e f f ect
r
(a,s
r
) denote the impact an actor a suffers
when resource r is in state s
r
. The global capacity of
action of actor a when the organization is in state s is
defined in this formalization as
payo f f (a,s) =
∑
r∈R
stake(a,r) ∗ e f f ect
r
(a,s
r
).
Within this setting, the actors of an organization coor-
dinate their respective behaviours while playing the so
called social game. An action of actor a on a resource
r that he controls is a move act
a
[r] to be applied to
the current state s
r
of r. A step of the game occurs
when each actor a has chosen a move act
a
[r
i
] for each
resource r
i
that he controls, and the game then goes
from state (s
r
1
,s
r
2
,...,s
r
M
) to state (s
0
r
1
,s
0
r
2
,...,s
0
r
M
),
where s
0
r
i
= s
r
i
+ act
a
[r
i
].
The game is repeated until it becomes stabilized,
or stationary: each actor has a satisfying payoff and
plays the null action, i.e., he no longer changes the
state of the resources he controls. Such a state of the
game is considered a social equilibrium, a regulated
situation that is satisfying and accepted by all the ac-
tors in the game. This state depends on the strategy
of each actor, i.e. how he adapts his behaviour (by
changing the state of the resources he controls) ac-
cording to the payoff he receives from others. In most
human organizations, social games are positive sum
games: each actor obtains some gain from being co-
operative, because others will also be cooperative in
return. Thus, typical social equilibria are Pareto max-
ima: any increase in an actor’s satisfaction would en-
tail a decrease of the satisfaction of another actor, and
thus produce a situation that would not be accepted
by all the actors.
3 THE EXTENDED
FRAMEWORK
The formalization of the coordination among the ac-
tors of an organization as shown above has some lim-
itations that do not allow it to handle some complex
organizations.
There exist cases in which the actors that are mem-
bers of an organization have different views on the set
of resources handled in that organization. Some ac-
tors may view a set of several resources as a single one
because they are unable to identify or to distinguish
the elements of such a compound resource, whereas
others may view each of those resources individually.
Also, a resource may be a substitute for another
one (having a good access to a resource makes it need-
less to have a good access to the other one), two re-
sources may be complementary (good access to one
resource is useful only if it goes together with a good
access to the other one), or they may have interactions
of some kind (if there is a good access to r
1
then r
2
is more important than r
3
, and the converse holds in
case of a bad access to r
1
). Moreover, these interac-
tions among resources may be different for different
actors.
The additive way used to compute the payoff of
actors as given in Section 2 is very restrictive; there,
the impact that the state of a resource has on an ac-
ICEIS 2008 - International Conference on Enterprise Information Systems
554

tor is independent on the state of any other resource.
Also, the stakes that the actors distribute on the re-
sources, that models the importance a resource has to
an actor, have to be precisely quantified.
Here we extend that formalization so that these
limitations can be overcome and a larger set of sit-
uations can be dealt with:
1. The control of a resource may be shared by sev-
eral actors; in such a case, each of these actors
contributes to the definition of the state of this re-
source according to his amount of control.
2. A resource may be composed of a set of resources.
3. The resources are no longer considered as being
independent: the actual effect of a resource on one
actor may depend on the state of another resource.
4. The payoffs may be calculated differently for each
actor.
5. Each actor is allowed to be imprecise in the way
he distributes the stakes on the resources that are
important to him.
3.1 Formalization of the Extended
Framework
We propose to formalize a social game in the follow-
ing way:
• A = {a
1
,...,a
N
} is a set of social actors.
• R = {r
1
,...,r
M
} is a set of resources, each of
which needed and controlled by some actors in
A (not necessarily the same ones). The state of a
resource r
i
at a given moment is given by variable
s
i
, that takes values in the interval [−1,1]; S de-
notes the set of state variables, and thus | S |=| R |.
The overall state of the game is defined by the
state of all the resources, described by a vector
s = (s
1
,s
2
,...,s
M
) ∈ [−1,1]
M
.
• R
◦
⊆ P(R) is the complete set of resources needed
to model a game, and an element r ∈ R
◦
is either
an elementary resource (a singleton) or a com-
pound resource.
• Function controls : A × R
◦
→ [0, 1] defines the
amount of control the actors exert on the resources
and is such that ∀r ∈ R
◦
,
∑
a∈A
controls(a,r) = 1
and ∀a ∈ A,∃r ∈ R
◦
,controls(a,r) > 0.
• Function impacts : R
◦
× A → {T,F} states
whether the state of resource r ∈ R
◦
has a direct
impact on an actor a ∈ A; when actor a depends
directly on resource r we have impacts(r,a) = T .
• The perception of an actor a on the state of a
resource r ∈ R
◦
at a given moment is denoted
by s
∗
a,r
. Each actor only perceives the resources
he depends on, i.e. s
∗
a,r
is defined only when
impacts(r, a) = T . The value of s
∗
a,r
is obtained
by means of a function of the state of r ∈ R when
r is a singleton, and as a function of the states of
the elementary resources composing r ∈ R
◦
, oth-
erwise.
• Function stake : A × R
◦
→ I
[0,10]
, where I
[0,10]
is
the set of intervals [a,b] ⊆ R such that 0 ≤ a ≤ b ≤
10, expresses how important it is for an actor to
access a resource, be it elementary or compound
1
.
Each actor has the same amount of stake points to
distribute among the resources he depends on di-
rectly and restrictions should be imposed to guar-
antee this constraint (see 4.3 for an example). For
a resource r ∈ R
◦
, stake(a,r) = [0,0] = 0 means
that a has no need for r, whereas stake(a,r) =
[10,10] = 10 means that r is the unique resource
needed by a. We have impacts(r, a) = T iff
stake(a,r) > 0.
• The payoff of each actor depends on his percep-
tion of states of the resources that have impact on
him, and can be calculated as in (Sibertin-Blanc
et al., 2006) or in a fuzzy framework as in (Sandri
and Sibertin-Blanc, 2007a).
3.2 Playing the Social Game in the
Extended Framework
The action of an actor a contributes to the modifica-
tion of the state of each resource r ∈ R
◦
according to
the amount of his control on r, given by controls(a,r).
The action of actor a is a vector act
a
with as many
positions as the number of resources he has some
control on, i.e. the size of act
a
is given by | {r ∈
R
◦
| controls(a,r) > 0} |. When a resource r is in
state s
r
and the actors with some control on r, col-
lected in A(r) = {a ∈ A | controls(a,r) > 0}, perform
their actions, the resulting state s
0
is computed by the
application of a function, that takes into account s
r
,
{act
a
[r] | a ∈ A(r)}, and {controls(a,r) | a ∈ A(r)}.
The payo f f of an actor a is computed taking into
account the states of the resources actor a depends on,
i.e. the resources in {r | impacts(r,a) = T }.
Thanks to the consideration of compound re-
sources, an actor can view a set of elementary re-
sources as a single compound resource r, and the the
specification of a function to calculate s
∗
a,r
allows us
to deal with any interaction among these resources.
1
The total amount of stakes to be distributed is fixed on
10 in accordance to previous works, but any other positive
value could be used.
A PARTIAL-VIEW COOPERATION FRAMEWORK BASED ON THE SOCIOLOGY OF ORGANIZED ACTION
555

Thus there is no longer a drawback to compute
the payo f f of an actor in a way that assumes that the
involved resources are independent: all interactions
are encapsulated into compound resources. Notice
that these interactions can be specific for each actor,
since it is possible to define two compound resources
r, q ∈ R
◦
such that r ∩ q 6=
/
0.
4 TREATMENT OF EXAMPLES
In the following we consider three examples of or-
ganizations to illustrate our framework. The third ex-
ample, Trouville, is a classical example from strategic
analysis taken from (Smets, 2004).
4.1 Two Clerks and One Boss
In an office, two clerks (C
1
and C
2
) work under a boss
(B). The boss controls 3 resources; the work hours of
the clerks (h) on any given day and the premium each
clerk receives at the end of the month on top of the
salary (p
1
and p
2
). Each clerk controls the amount of
work he does during the day (w
1
and w
2
). The boss
depends on resource w, the composition of resources
w
1
and w
2
, clerk C
1
depends on p
1
and h and clerk C
2
depends on p
2
and h.
Everyday, the clerks take documents from the in
pile
2
that have to be processed during that day. After
a clerk finishes with a document, he signs it, lays it on
the out pile and takes a new one from the in pile. The
boss does not verify every day which clerk did what
during that particular day, although the signature on
each document is verified before the end of the month.
When the boss sees that the in pile is empty, it is up
to him to give the clerks the rest of the day off.
Figure 1 illustrates the case. The set of actors
is given by A = {B,C
1
,C
2
}, and the set of elemen-
tary and compound resources are respectively given
by R = {p
1
, p
2
,h,w
1
,w
2
} and R
c
= {{w
1
,w
2
}} =
{w}. In the figure, the edges from an actor a to
a resource r ∈ R ∪ R
c
stands for controls(a,r) > 0,
whereas the edges from a resource to an actor rep-
resents impacts(r, a) = T . We assume that each re-
source r controlled somewhat by an actor a has an
impact on a but we chose not to represent that impact
explicitly in the figure.
The set of state variables, resulting from ac-
tions taken by the controllers of each resource, is
given by S = {s
p
1
,s
p
2
,s
h
,s
w
1
,s
w
2
}. The set of
2
We consider here that the amount of work on the in pile
on any given day is set by an actor that is not relevant for
the relations between the boss and the clerks under him.
Figure 1: Structure of an organization with two clerks and
one boss.
states perceived by the actors is given by S
∗
=
{s
∗
C
1
,h
,s
∗
C
2
,h
,s
∗
C
1
,p
1
,s
∗
C
2
,p
2
,s
∗
B,w
}, which we simplify to
S
∗
= {s
∗
1h
,s
∗
2h
,s
∗
1p
,s
∗
2p
,s
∗
Bw
}.
The actors may perceive the state of the resources
in various ways. For example, we could have s
∗
1h
=
s
∗
2h
= s
h
, s
∗
1p
= s
p
1
and s
∗
2p
= s
p
2
. In this case, the
state of elementary resources perceived by the ac-
tors are the same as the states of the resources them-
selves. In what regards compound resources, the per-
ception of an actor is always a function of the state
of the elementary resources composing it. The per-
ception of the boss in relation to the work done by
the clerks at the end of a day could be given for in-
stance by s
∗
Bw
= (s
w
1
+ s
w
2
)/2. The payoffs of the
actors are calculated using the perceived state of the
resources they depend upon. An example of payoff
is for instance payo f f (C
1
) = 10 × min(s
∗
1h
,s
∗
1p
) and
payo f f (C
2
) = 10 × max(s
∗
2h
,s
∗
2p
). Note that due to
the way they aggregate their perception of reality, C
1
is more pessimistic and is less satisfied than C
2
even
when the they receive the same premium and leave at
the same time.
4.2 Two Bosses and One Clerk
In an office, a clerk (C) works under two bosses (B
1
and B
2
). The clerk controls the amount of work he
does during the day (w). Each boss controls one re-
source individually: the workload each one of them
assigns to the clerk (l
1
and l
2
). The total workload
of the clerk is represented by compound resource l, a
composition of l
1
and l
2
. The bosses control together
the job stability of the clerk ( j). The bosses set the
state of resources l
1
and l
2
independently (with the
proviso that each one has a maximum workload to as-
sign), whereas the state of resource j is set by them
by common accord. In Figure 2 we illustrate the ex-
ample; note that in the figure we do not represent ex-
plicitly the edge from an actor to any of the resources
he somewhat controls.
Given that j is controlled conjointly, to facili-
tate visualization, we created a dummy node in the
graph to represent their agreement. The edges be-
tween nodes B
1
and B
2
and the dummy node are la-
ICEIS 2008 - International Conference on Enterprise Information Systems
556

Figure 2: Structure of an organization with two bosses and
one clerk.
beled with the amount of control of the secretary’s
job stability as set by each boss. Here we have
weight .7 for B
1
and .3 for B
2
, and thus boss B
1
has
a stronger influence on the state of j than B
2
. Let
us suppose that the value of the state of j is calcu-
lated with the weighted arithmetic means. In this case,
we would obtain s
0
j
= s
j
+controls(B
1
, j)×act
B
1
[ j]+
controls(B
2
, j) × act
B
2
[ j] = s
j
+ .7 × act
B
1
[ j] + .3 ×
act
B
2
[ j].
Contrary to the case of compound resources, here
we do not create a formal “compound actor”. Actu-
ally, we could represent this situation using two ex-
tra resources, j
1
and j
2
, each of which controlled by
one the bosses. However, here we want to make a
difference between an independent control of com-
pound resources, as shown in Figure 1 where w
1
and
w
2
compose w, and a control by agreement as shown
in Figure 2.
4.3 Trouville
Travel-tours is a tour operator that has two agencies,
TRO1 and TRO2, in Trouville. The directors of TRO1
and TRO2 have a secretary, Agn
´
es, who works for
both of them. She works half a day in each agency,
what obliges her to move between the two jobs every-
day, and her contract has to be extended every month
as her position is not a stable one.
Lately, the results of TRO1 have increased,
whereas the ones of TRO2 have stagnated, or even
decreased. The regional director decides to reward
TRO1 for its merits and proposes to regularize the sit-
uation of Agn
´
es and to affect her exclusively to TRO1.
However, both Agn
´
es and Paul (the director of
TRO1), vigorously refuse the proposal, which seems
counterintuitive: Agn
´
es would hold a permanent po-
sition and would not have to split her work and time
in two parts, whereas Paul would have a full-time sec-
retary at his disposal in TRO1. A strategic analysis,
by identifying the uncertainty zones, shows that both
Paul and Agn
´
es are rationally right to be opposed to
this organizational change, because it would decrease
their respective power.
Figure 3: The structure of the Travel-Tours example.
Indeed, a more attentive analysis of the case re-
veals that TRO2 is more inventive than TRO1 in de-
signing travel packages, while TRO1 includes a very
efficient commercial staff; being aware of the TRO2
agency’s activity, the secretary provides information
to the director so that TRO1 takes full advantage of
finalizing TRO2’s ideas. On the other hand, for per-
sonal reasons, to get a steady job is not one of Agn
´
es’
short-time objectives. Moreover, she greatly appreci-
ates that none of the directors has the possibility to
exert a precise control on her work.
Thus the situation shift would increase the control
of the director on the secretary’s activities (something
she does not want), and the director would lose the in-
formation given by the secretary on TRO2 (something
he does not want).
In previous works, we modeled this example con-
sidering only two actors, Paul and Agn
´
es (Sandri and
Sibertin-Blanc, 2007a) (Sandri and Sibertin-Blanc,
2007b). Here we modify slightly this setting to in-
clude a new actor, the director of TRO2. He is
not aware that Agn
´
es is taking information from his
agency to give to TRO1, and is basically interested
that she continues to work to TRO2 and that she ac-
complishes the tasks he assigns her.
Here we implement the example using three ac-
tors A = {D
1
,D
2
,S}, where D
1
and D
2
stand for
the directors of TRO1 and TRO2, respectively, and
S for the secretary. We have five simple resources
R = {i,l
1
,l
2
, j
1
, j
2
}, where i stands for the informa-
tion provided by the secretary, l
1
and l
2
represent the
workload set by each director to the secretary, and j
1
and j
2
stand for the job stability set by each director to
the secretary. We also have two compound resources,
l = {l
1
,l
2
} and j = { j
1
, j
2
}, that stand for the total
workload and job stability of the secretary. In Fig-
ure 3 we illustrate the example (the edges between an
actor to the resources he controls are omitted).
The stakes that each actor places on the resources
are illustrated in Figure 4. There exists a labeled edge
between each actor and a resource that has any im-
pact on him (including those he somewhat controls);
the thin dotted ones represent those he has absolutely
no control on. The larger dotted edges connect a com-
A PARTIAL-VIEW COOPERATION FRAMEWORK BASED ON THE SOCIOLOGY OF ORGANIZED ACTION
557

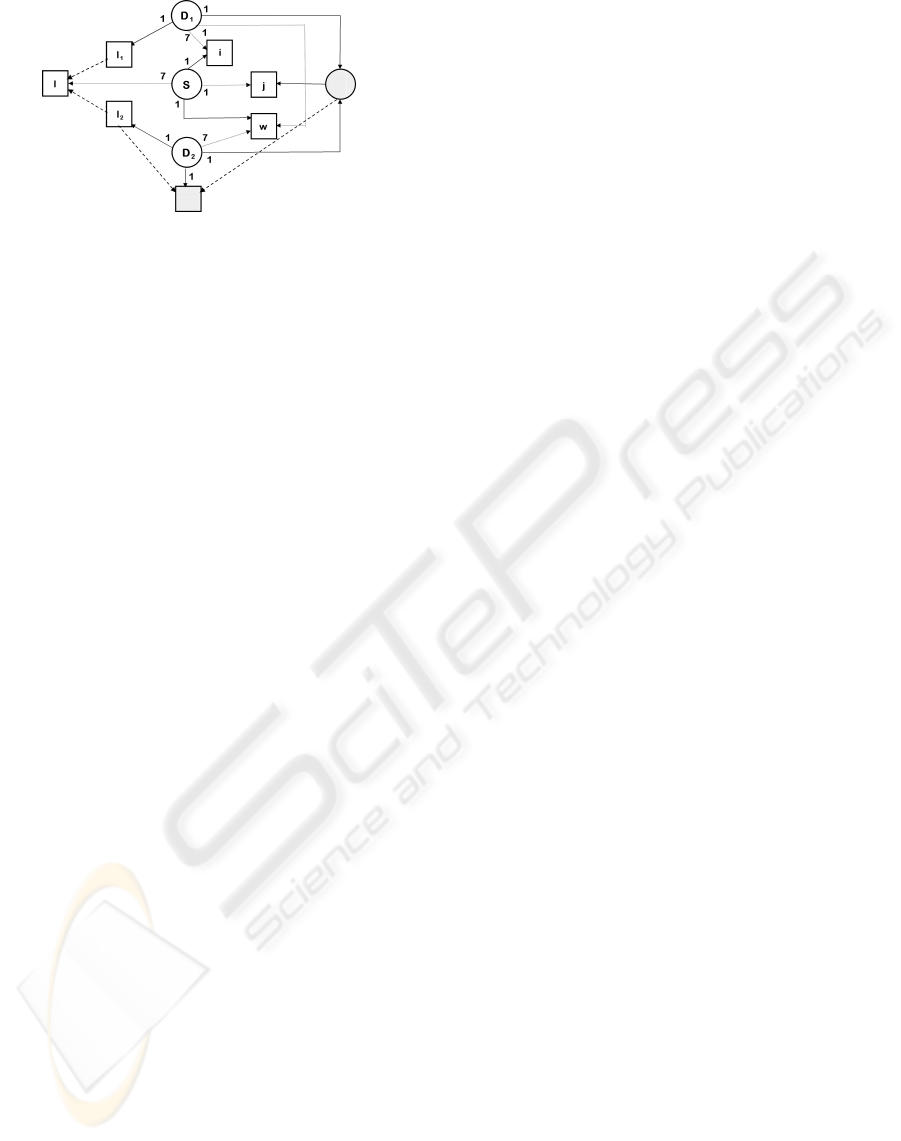
Figure 4: Stakes assignment in Travel-Tours example.
pound resource to its components.
The values were assigned considering the actors’
attitudes. The more the secretary gives information
from TRO2 to TRO1, the best it is for its director, who
uses it to improve the activity of TRO1 agency, but
the worse it can be for herself if someone from TRO2
discovers that she provides information to TRO1.
The director of TRO1 puts a high stake on the in-
formation resource (as far as the social game is re-
stricted to his relations with the secretary) because
bringing this information is the most important con-
tribution of the secretary to the agency, whereas giv-
ing or not the information does not have a high effect
on her. Similar considerations explain the values he
assigns to the stability of the job and control of work
resources. The director of TRO2 cares a little for both
the secretary’s job stability and content, but cannot
be bothered to completely distinguish the individual
value of these resources to him up to a point. Here
we modeled D
2
’s attitudes as stake(D
2
, j) = [a
j
,b
j
] =
[1,2] = [a
l
,b
l
] = stake(D
2
,l), and created a dummy
compound resource to represent that the constraint
that, according to D
2
, the total amount of stakes for
the secretary’s job taken as a whole adds up to 3, i.e.
a
j
+b
l
= a
l
+b
j
. Thus, the secretary’s job situation is
not so important to the director as the amount of work
she does (which gets 7 stakes).
The stakes can be used to calculate payoffs but
also to model concepts such as the autonomy and sub-
ordination of an actor (Sibertin-Blanc et al., 2006).
The first (respec. the second) concept is modeled as
the sum of the stakes an actor puts on resources he
controls (respec. does not control); together, the au-
tonomy and the subordination of an actor add up to
10. Here these concepts have to be extended to han-
dle stake intervals and shared control. Let the min-
imal subordination (respec. minimal autonomy) be
the sum of stakes an actor places on resources he has
absolutely no control upon (respec. he certainly has
absolute control upon). Then the pair (autonomy, sub-
ordination) are respectively given as ([1,2],[8,9]) for
D
1
, by ([1,3],[7,9]) for D
2
and by ([2,2],[8,8]) =
(2,8) for S.
5 CONCLUSIONS
We presented a cooperation framework based on the
Sociology of Organized Action, that makes it possi-
ble to model the different views actors may have on
the resources of an organization, and that allows a re-
source to be controlled by more than one actor.
We intend to use it to model problems in crisis
management, in which an actor has a partial rep-
resentation of a crisis, focusing on the aspects that
are important to solve his part of the problem; less
important aspects are not perceived accurately, but
through a general framework. As future work we
intend to incorporate the notion of time in our frame-
work, to make it closer to reality, since the actors
usually receive information at different times during
a crisis and their vision may not be synchronized.
ACKNOWLEDGEMENTS
This work was partially supported by the Span-
ish Project Autonomic Electronic Institutions (TIN-
2006-15662-C02-01 ) and by the Generalitat de
Catalunya under grant 2005-SGR-00093.
REFERENCES
Crozier, M. (1964). The Bureaucratic Phenomenon. Univ.
of Chicago Press.
Crozier, M. and Friedberg, E. (1995). Organizations and
collective action: our contribution to organizational
analysis. In S.B. Bacharrach, P. Gagliardi and B.
Mundel (Eds), Studies of Organizations in the Euro-
pean Tradition. Jay-Press.
Mailliard, M., Audras, S., and Marina, C. (2003). Multia-
gents systems based on classifiers for the simulation
of concrete action systems. In Proc. EUMAS’03. Ox-
ford University (UK).
Sandri, S. and Sibertin-Blanc (2007a). Transposing the so-
ciology of organized action into a fuzzy environment.
In Proc. ECSQARU’07. Hammamet (Tu), pp. 791–
802.
Sandri, S. and Sibertin-Blanc, C. (2007b). A fuzzy rule-
based modeling of the sociology of organized action.
In Proc. CCIA’07. S.J. de L
´
oria (An), pp. 281–290.
Sibertin-Blanc, C., Amblard, F., and Mailliard, M. (2006).
A coordination framework based on the sociology of
organized action. In Coordination, Organizations, In-
stitutions and Norms in Multi-Agent Systems. Olivier
Boissier, J. Padget, V. Dignum, G. Lindemann (Eds.).
Springer Verlag, LNCS 3913, pp. 3–17.
Simon, H. (1996). The sciences of the artificial. MIT Press,
3rd edition.
Smets, P. (2004). L’agence travel-tours. In
http://homepages.ulb.ac.be/ psmets1/travel.pdf.
ICEIS 2008 - International Conference on Enterprise Information Systems
558