A STUDY OF THE SPATIAL REPRESENTATION IN

MULTIDIMENSIONAL MODELS

Concepción M. Gascueña

Department of Computing, Carlos III de Madrid University, Avd. University 30, 28911 Leganés, Spain

Rafael Guadalupe

Department of Topographic, Politécnica de Madrid University, Carretera de Valencia Km7, 28031 Madrid, Spain

Keywords: Data Structures, Databases, Database Theory, Multidimensional Databases, Spatial Granularity Semantics,

Spatio-Temporal Multigranularity Semantics, Databases and Information Systems Integration.

Abstract: In this work, we do an analysis on the different models proposed to model Multidimensional Databases

MDB, and Spatial Databases SD. We analyze the basic and advanced rules that the conceptual

multidimensional models should to support, according sort criterion exposed for some authors. As result of

this study, we propose to add new rules to gather the spatial and temporal semantics. Are analyzed some of

models more relevant, and a comparative table is presented, where the advantages of the model called

FactEntity FE, with respect to the other examined modes, to collect multidimensional and spatial semantics,

is obvious. We emphasizing on the novel contributions of FE model and shortcomings of the rest of seen

models. We besides show a formalization of the FE model with a metamodel made up with the extended ER

model, where the semantics of FE model is representing. Finally, an example of application clarifies our

exposure.

1 INTRODUCTION

The Decision Support Systems and the Geographic

Information Systems GIS, use the Data Warehouses

or Multidimensional Databases MDB. The GIS

locates spatial data on the Earth’s surface and

studies its evolution through time. The

Multidimensional databases MDB, allow the storing

of data in a special way to study these from different

perspectives or dimensions and with different detail

levels or granularities. The most proposals to model

MDB reuse the models of operational databases DB,

as the Entity Relation ER, or the Unified Modelling

Language UML, although they are not appropriating

to model these databases, since, they were conceived

for other purposes. We believe as the authors in

(Golfarelli, 1998), (Torlone, 2003), (Kimball, 1996)

, that traditional conceptual models are not able to

express all the semantics of the MDB, and we too

are in agreement with (Piattini, 2006), which speak

on the immaturity of multidimensional technologies.

In addition, the GIS, require models that support

the process of reasoning about space, and that allow

us to gather spatial data in different scales

connected, as is commented in (William, 2006). For

all above, we believe that specific models, that can

to collect the multidimensional semantics and spatial

semantics, are needs.

In this work, we are going to study on the one

hand, the proposals that are to model MDB; and on

the other hand, the proposals that are to include the

space in the DB in general. In addition, we do a

comparative study on several of more relevant

models, to analyze how they to deal the spatio-

temporal multigranularities. We stress the proposal

in (Gascueña, 08), where the model called

FactEntity FE, is presented, which permit us to

collect multidimensional and spatial semantics. The

FE model allows treating the different types of

spatial granularity, Semantic and Geometric, which

in the study of (Gascueña, 08), are distinguished.

This model supports related spatial, temporal and

thematic granularities interacting between them.

None of the models studied collect previous

characteristics.

339

M. Gascueña C. and Guadalupe R. (2008).

A STUDY OF THE SPATIAL REPRESENTATION IN MULTIDIMENSIONAL MODELS.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - DISI, pages 339-348

DOI: 10.5220/0001715503390348

 SciTePress

This paper is structuring, as follows: Section 2

includes a extend study on related works in

multidimensional and spatial semantics and in

addition, the rules provided by some authors, as

necessary to the conceptual multidimensional MD,

models, along other new rules, are exposed. Besides,

a comparative table, between some more relevant

model and the FE model, is showing. In Section 3,

we present briefly the FE model, which include

graphical representation and a Metamodel. The

Section 4 includes an illustrative example. In section

5, some conclusions and future work are given.

2 RELATED WORK

Most of the models proposed to design MDB from a

conceptual approach, are basing on concepts

modelled from traditional DB and present extensions

to the ER model such as in (Sapia, 1999). Other

models, (Malinowski, 2004a) and (Golfarelli, 1998),

adopt the starting point of an ER model providing

guidelines for its transformation into a

multidimensional MD model. In the StarER model

(Tryfona, 1999) , there is a proposal to use the Star

multidimensional model together with an extension

of the ER model. Other authors such as (Lujan-

Mora, 2006) and (Abello, 2006) present extensions

to the UML model. Although researchers such as

(Torlone, 2003) and (Kimball, 1996) consider, as we

do, that the traditional data models are not adapted

to represent the special semantics of MDB. Some

classifications of the most important characteristics

that must be gathered in a conceptual MD model, are

shown in (Torlone, 2003), (Abello, 2000),

(Malinowski, 2004a), and (Lujan-Mora, 2006). The

authors in (Abello, 2000), propose to design the

conceptual phase in three levels of detail increasing

in complexity; with this design approach, a model

called YAM2 presenting in (Abello, 2002), and

(Abello, 2006), which uses an extension of UML

model. The model in (Torlone, 2003) is presenting

from a conceptual point of view and it specifies the

basic and advanced characteristics that an ideal

conceptual MD model would have. In (Lujan-Mora,

2006) the cardinalities in the hierarchies are

considering and classified with concepts such as

strictness and completeness; in addition, the additive

of measures and the representation of some

aggregation operators are exposed; they use the

language Object Constraint Language (OCL) to

specify constraints. A classification of the different

hierarchies (with regard to the cardinality between

the different hierarchical levels) that must support a

model is presenting in (Malinowski, 2004a). This

work is completing in (Malinowski, 2005), where it

is defining as transforming these hierarchies into the

logical model under the relational paradigm.

2.1 Space and Time in MDMs

Three types of space dimensions (depending on

whether the space elements are included in all, some

or none of the levels of the dimensional hierarchies)

and two types of measures (space or numerical

measures) are distinguishing in (Stefanovic, 2000).

In (Malinowski, 2004a) the inclusion of the spatial

data at a level of a hierarchy or as measures is

proposing, though they do not include the spatial

granularity. In (Malinowski, 2005), the same authors

present a classification of the space hierarchies

following the criteria set in (Malinowski, 2004a),

(with regard to the cardinality). A study is presenting

on the temporality of the data at column and row

level in (Malinowski, 2006). None of the previous

works contemplates spatio-temporal

multigranularity. In (Gascueña, 2006) is studied the

multigranularity of the spatial data from a logical

approach. In (Gascueña, 2005) is detailed a

comparative view of how to deal the spatio-temporal

multigranularity with two different logical models:

Object Oriented (OO) and Multidimensional. In

(Gascueña, 2008) is presented the specific

FactEntity multidimensional model, from a

conceptual approach, which gather the spatio-

temporal multigranularities. In addition, these

authors make up a study on how to represent the

spatial granularity in a MDB, and distinguish

between Semantic and Geometric granularities.

2.2 Space and Time in OO Models

The treatment of the multigranularity in OO models

exists, as in the work of (Camossi, 2003) that

extends Object Data Management Group (ODMG),

for the inclusion of this concept in its model called

Spatio Temporal ODMG (T_ODMG). The

ST_ODMG model supports the handling of entities

with a spatial extension that changes their position

on temporary maps. It provides a frame for mapping

the movement of a moving spatial entity through a

geographic area, where the spatial objects can be

expressing at different levels of detail.

In (Khatri,

2006) a study on the spatio-temporal granularities by

means of ontology is carrying out. They propose to

model it in two phases: first, by using a conventional

conceptual ER model, without considering spatial or

temporal aspects, it would model “what”. In the

ICEIS 2008 - International Conference on Enterprise Information Systems

340

second phase, it completes with notations or labels

that gather the associated semantics of time and

space, “when and where”, as well as the movement

of the spatial objects, although they only handle one

granularity for each spatial data. In (Parent, 1999) it

shows the MADS model as an extension of the ER

model, although it uses elements OO and some

authors present it as a hybrid between OO and ER. It

uses complex structures and abstract types of data to

support the definition of domains associated with

space and time over object and relations. But none

of the proposed models above distinguish, between

Semantic and Geometric spatial granularities, as we

do.

2.3 Multi-representation

In reference (Parent, 2006) an extension to the MAD

model is added to handle multiple resolutions in the

geographic databases. It presents four orthogonal

dimensions in order to model: data structures, space,

time and representation. It distinguishes two

approaches to support multiple spatial resolutions.

The multi-resolution approach only stores the data of

the upper level of resolution, delegating the

simplification and space generalization to the

databases system. The multi-representational

approach stores the data at different levels of

resolution and allows the objects to have multiple

geometries. In (Bedard, 1999) and (Borges, 2001)

objects with different interpretations and scales are

defined. In (Timpf, 1999) series of maps, are used

and handle with hierarchies. In (Jones, 1996) objects

with different representations (multi-scale) are

associated. In (Sell, 1998) the objects at different

levels of detail are organized, such as stratified

maps. In (Bedard, 2002) the concept of “VUEL”

(View Element) and new definitions of multi-

representation are introduced with four dimensions:

semantics, graphic, geometry and associated scale. It

proposes to model the space using the expressivity

of the MD models, where the spatial data is dealt

with in the table of facts and the dimensions are

marking the different semantics of multi-

representation, although it is not a MD

multidimensional. The Geo_Frame-T model

(Vargas, 2001) uses the OO paradigm and an

extension of UML model, and introduces a set of

temporal and space stereotypes to describe the

elements and the class diagram. The Temporal

Spatial ER STER, model is presented in (Tryfona,

2003) as an extension of the ER model maintaining

the concepts used in ER and including sets of spatial

entities. In (Le, 2005) space and temporal data

models for Temporal GIS is proposed. The

integration of multiple representations is basing on

common spatial and temporal reference systems. It

uses layers to keep the spatial data, one layer for

each space representation in a determined time. For

the evolution through time, it uses a layer for each

spatial element and every moment of time. It

distinguishes between temporal representations

based on characteristics and data models based on

layers. It uses the map itself with different thematic

data in the time interval itself.

None of these models support multidimensional

concepts, for this reason they are not adapted to

model the multidimensional semantic; in addition

neither do they distinguish between Semantic and

Geometric spatial granularities. The study done in

(Gascueña, 2008) separate the way of divide a space

of interest for semantic qualities; and the way to

store this space by geometries in a DB; and in

addition, the way of represent this space in a

computer, when it is recovered from a DB.

This section has carried out the study of data

models from the focus of MDB and from the focus

of DB in general. It has verified that a great effort

have been made, to gather the space and temporal

characteristics of the data in traditional models. But,

there are not specific approaches for the MD models

that gather the spatio-temporal multigranularities

considered in (Gascueña, 2008), only the FE model

define their own constructors to gather the specific

multidimensional and spatio-temporal semantics,

which justifies our proposal to use the FE model.

2.4 Rules to the MD models

The authors in (Blaschaka, 98), (Pedersen, 00),

(Torlone, 01), (Abello, 00), (Abello, 02),

(Malinowski, 04a), propose the basic and advanced

rules that the conceptual MD models must comply.

We look these in Tables 1, 2, 3 and 4.

Table 1: Basic rules according to (Pedersen, 2000),

(Blaschaka, 1998), (Torlone, 2001).

Explicit separation of structure and content

Explicit notions of dimension and data cube

Explicit hierarchies in dimensions

Multiple hierarchies in each dimension

Level attributes

Measures sets

Symmetric treatment of dimensions and measures

Explicit separation of structure and content

Explicit notions of dimension and data cube

Explicit hierarchies in dimensions

Multiple hierarchies in each dimension

Level attributes

Measures sets

Symmetric treatment of dimensions and measures

A STUDY OF THE SPATIAL REPRESENTATION IN MULTIDIMENSIONAL MODELS

341

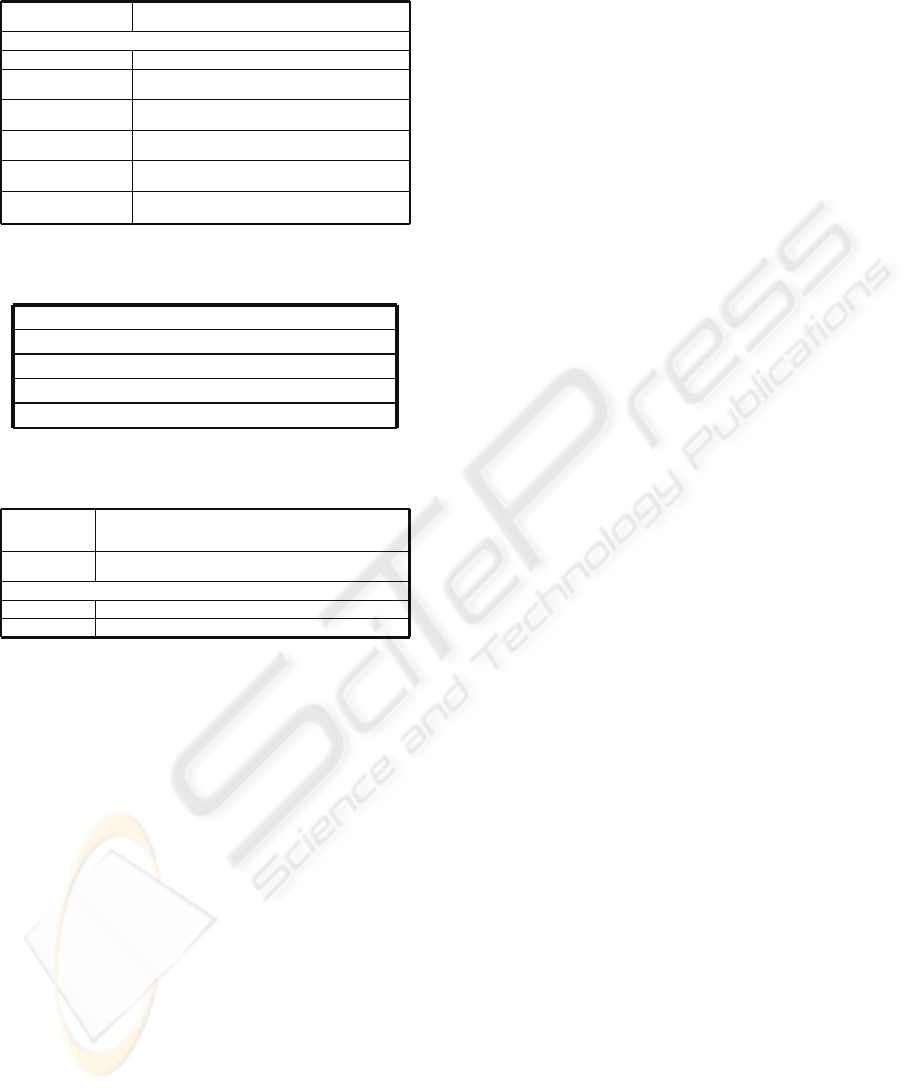
Table 2: Advanced characteristics proposal for (Torlone,

2001).

Support for semantic

aggregations

The FE model include explicit specification over as to make up

the aggregation

Support for non standard aggregations of facts

Non-strict hierarchies Relationship (N:M) between parent/child levels of dimensions

Non-onto hierarchies

Parent level without representation in child level. We control this

whit the cardinalities (1,1)Æ (0,n)

Non covering hierarchies

Child level without representation in inmediate superior parent

level. We control this whit the cardinalities (0,1)Æ (1,n)

Many relationships between

facts and dimensions

We think that it is not semantically correct, though our model

allows its representation

Handling change and time

The FE model incorporates: Temporal factEntity, Temporal level

and Temporal attribute

Handling vagueness

The FE model allow us to include all the semantic necessary for

what this problem to be known and controlled.

Support for semantic

aggregations

The FE model include explicit specification over as to make up

the aggregation

Support for non standard aggregations of facts

Non-strict hierarchies Relationship (N:M) between parent/child levels of dimensions

Non-onto hierarchies

Parent level without representation in child level. We control this

whit the cardinalities (1,1)Æ (0,n)

Non covering hierarchies

Child level without representation in inmediate superior parent

level. We control this whit the cardinalities (0,1)Æ (1,n)

Many relationships between

facts and dimensions

We think that it is not semantically correct, though our model

allows its representation

Handling change and time

The FE model incorporates: Temporal factEntity, Temporal level

and Temporal attribute

Handling vagueness

The FE model allow us to include all the semantic necessary for

what this problem to be known and controlled.

Table 3: Characteristics proposed for (Abello, 2000),

(Abello, 2002).

It allows us to see several fact in a scheme

Identification of facts

Mathematical constructs used for operations

Elements over which operations are defined

User defined aggregation functions

It allows us to see several fact in a scheme

Identification of facts

Mathematical constructs used for operations

Elements over which operations are defined

User defined aggregation functions

Table 4: Characteristics proposed for (Malinowski,

2004b).

Symmetrical

hierarchy

For each member m of a level there at least a member m’ of the inferior

level and for each member m’ of a level there only a member m of the

superior level. Cardinality (1,1) Æ (1,n) parent/child

Multiple alternative

hierarchies

Several non-exclusive simple hierarchies sharing some levels but with the

same analysis criterion.

Parallel hierarchies: A dimension has several hierarchies but with different analysis criterion

Dependent Different hierarchies sharing some levels

Independent Different hierarchies do not sharing levels.

Symmetrical

hierarchy

For each member m of a level there at least a member m’ of the inferior

level and for each member m’ of a level there only a member m of the

superior level. Cardinality (1,1) Æ (1,n) parent/child

Multiple alternative

hierarchies

Several non-exclusive simple hierarchies sharing some levels but with the

same analysis criterion.

Parallel hierarchies: A dimension has several hierarchies but with different analysis criterion

Dependent Different hierarchies sharing some levels

Independent Different hierarchies do not sharing levels.

We also added the following rules, to gather the

spatial component:

Spatial Multigranularity (it is support for the

multi-representation): Semantic and Geometric

granularities.

Temporal Multigranularity into different

structures: factEntity, hierarchical level, attribute.

Spatio-Temporal Multigranularity is the

possibility to represent on the scheme different

granularities related and interacting. The FE model

in (Gascuenña, 2008) supports all the previous

characteristic.

2.5 A View Comparative between some

Models

Table 5 shows a comparison between some of the

most outstanding models. We observe that in

(Trifona, 2003), (Golfarelli, 1998), (Sapia, 1999),

(Abello, 2006), and (Torlone, 2001), they do not

support all the multidimensional hierarchies

proposed in for (Ma&Zi, 2004b), this work does the

classification of hierarchies with regard to the

cardinalities. Only the FE model in (Gascueña,

2008) supports the temporal multigranularities in all

the structures as factEntity, hierarchical level, and

attribute.

The Semantic and Geometric spatial granularities are

not defined and therefore do not supports, for any

models excepting the FE model, although some

authors as (Parent, 2005), (Khatri, 2006), (Trifona,

2003), (Malinowski, 2004a) consider the spatial

granularity of different way as we do. The models

(Trifona, 1999a), (Sapia, 1999a), (Torlone, 2001)

not representing multiple facts in the scheme. The

explicit aggregation of measures, that is, the explicit

representation of the functions that are applied to

each measure fact, when the granularities change, is

partially gathered in (Tryfona, 2003), (Lujan-Mora,

2006), (Golfarelli, 1998), (Sapia, 1999a), (Abello,

2006), and is not gathered in (Torlone, 2001), and

(Malinowski, 2004a), the FE model in (Gascueña,

2008) gathers totally this characteristic. In addition,

any of the models studied, except (Gascueña, 2008),

represent the spatial conversion functions that are to

apply when a spatial element changes to a coarser

granularity. In conclusion, only the FE model

supports completely all the characteristics shown in

Table 5, from a conceptual multidimensional

approach.

3 FACTENTITY MODEL

A multidimensional model allows us to study certain

facts under the perspective of certain dimensions and

with different levels of detail or granularities. We

show briefly The FE model, for more details see

(Gascueña, 2008).

3.1 Spatial Characteristics

We define a Spatial data type as an abstract data

type that contains an identifier, a unit of

measurement within a given reference system, a

geometry of representation associated with this unit,

and a dimension associated with this geometry.

Points associated to kilometers are examples of

geometrics associated to units in a reference system.

See table 6.

ICEIS 2008 - International Conference on Enterprise Information Systems

342

Table 5: Comparing models.

Y = yes NT = no otallly N = no L = logical C = conceptual OO = object oriented R = relational

- = the script means that the model does not contemplate that characteristic

Y = yes NT = no otallly N = no L = logical C = conceptual OO = object oriented R = relational

- = the script means that the model does not contemplate that characteristic

[Parent,05] MADS C E/R&UML OO N - NT NT - - -

[Khatri,06] DISTILL CE/RRN-NTNT---

[Tryfona,03] STER CE/RRN-NTNT---

[Tryfona,99] StarER C E/R R Y NT NT N N NT N

[Luján-Mora,06]

MDLujan-Mora

C UML OO Y Y NT N Y NT N

[Golfarelli,98b] DF C E/R R Y NT NT N Y NT N

[Sapia,99a] M/ER C E/R R Y NT NT N N NT N

[Abelló,06] YAM2 CUMLOOYNTNTNYNTN

[Torlone,01]

MDTorlone

C - RYNTNTNNNN

[Malinowski,04a]

SpatialMultiDiER

C E/R RYYNTNYNN

[Gascueña, 08]

FactEntity

C--R/&

YYYYYYY

Enfoque

Extension

Paradigm

Multidimensional

Hierarchies

(cardinality)

Temporal

Multigranularity

Spatial

Multigranularity:

Geometric/Seman.

Multi Facts

Explicity

Agregation of

Measures

Function to change

the Granularity

[Parent,05] MADS C E/R&UML OO N - NT NT - - -

[Khatri,06] DISTILL CE/RRN-NTNT---

[Tryfona,03] STER CE/RRN-NTNT---

[Tryfona,99] StarER C E/R R Y NT NT N N NT N

[Luján-Mora,06]

MDLujan-Mora

C UML OO Y Y NT N Y NT N

[Golfarelli,98b] DF C E/R R Y NT NT N Y NT N

[Sapia,99a] M/ER C E/R R Y NT NT N N NT N

[Abelló,06] YAM2 CUMLOOYNTNTNYNTN

[Torlone,01]

MDTorlone

C - RYNTNTNNNN

[Malinowski,04a]

SpatialMultiDiER

C E/R RYYNTNYNN

[Gascueña, 08]

FactEntity

C--R/&

YYYYYYY

[Parent,05] MADS C E/R&UML OO N - NT NT - - -

[Khatri,06] DISTILL CE/RRN-NTNT---

[Tryfona,03] STER CE/RRN-NTNT---

[Tryfona,99] StarER C E/R R Y NT NT N N NT N

[Luján-Mora,06]

MDLujan-Mora

C UML OO Y Y NT N Y NT N

[Golfarelli,98b] DF C E/R R Y NT NT N Y NT N

[Sapia,99a] M/ER C E/R R Y NT NT N N NT N

[Abelló,06] YAM2 CUMLOOYNTNTNYNTN

[Torlone,01]

MDTorlone

C - RYNTNTNNNN

[Malinowski,04a]

SpatialMultiDiER

C E/R RYYNTNYNN

[Gascueña, 08]

FactEntity

C--R/&

YYYYYYY

C E/R&UML OO N - NT NT - - -

[Khatri,06] DISTILL CE/RRN-NTNT---

[Tryfona,03] STER CE/RRN-NTNT---

[Tryfona,99] StarER C E/R R Y NT NT N N NT N

[Luján-Mora,06]

MDLujan-Mora

C UML OO Y Y NT N Y NT N

[Golfarelli,98b] DF C E/R R Y NT NT N Y NT N

[Sapia,99a] M/ER C E/R R Y NT NT N N NT N

[Abelló,06] YAM2 CUMLOOYNTNTNYNTN

[Torlone,01]

MDTorlone

C - RYNTNTNNNN

[Malinowski,04a]

SpatialMultiDiER

C E/R RYYNTNYNN

[Gascueña, 08]

FactEntity

C--R/&

YYYYYYY

Enfoque

Extension

Paradigm

Multidimensional

Hierarchies

(cardinality)

Temporal

Multigranularity

Spatial

Multigranularity:

Geometric/Seman.

Multi Facts

Explicity

Agregation of

Measures

Function to change

the Granularity

Table 6: Spatial data and topological relations.

Cros Point and LinePoint

Cross Line and LineLine

Cross Surface and LineSurface

Topological RelationshipaSapatial Data Type

Cros Point and LinePoint

Cross Line and LineLine

Cross Surface and LineSurface

Topological RelationshipaSapatial Data Type

Spatial granularity is the chosen detail level to

analyse the spatial data. We distinguish two types

Semantic and Geometric granularities. The Semantic

spatial granularity considers space divided by

means of a semantic characteristic; for example

political limits countries, etc. In Table 7, we can see

some spatial functions used when the Semantic

granularity changes. A set of Semantic

granularities enables us to consider the space

divided as bigger or smaller units that are “part-of”

a total, where, each part is considered a unique

spatial element.

Table 7: Spatial functions.

User Defined

Median, most frequent, rank,… Required new calculations using

the data of the leaf level

Holistic

Average, Variance, Standard deviation,… Need an additional

treatment for reusing the values

Algebraic

Sum, Min, Max,… Reuse aggregates of a lower level of a

hierarchy in order to calculate the aggregates for higher level

Distributive

User Defined

Median, most frequent, rank,… Required new calculations using

the data of the leaf level

Holistic

Average, Variance, Standard deviation,… Need an additional

treatment for reusing the values

Algebraic

Sum, Min, Max,… Reuse aggregates of a lower level of a

hierarchy in order to calculate the aggregates for higher level

Distributive

A Geometric spatial granularity is defining as

the unit of measurement, in a space reference

system, associated with geometry of representation.

A set of Geometric spatial granularities allow

representing the same spatial data in different forms

and size in a moment of time. In table 8, we can see

some functions used when the Geometric spatial

granularity changes the other greater one.

Table 8: Spatial conversion functions (Berloto, 1998).

It contracts an open line, endpoints included, to a pointl_contr

It contracts a simple connect region and its boundary to a pointr_contr

Absorption operations ….

Merge, functions …….

It reduces a region and its boundary lines to a liner_thinning

Contract functions

It contracts an open line, endpoints included, to a pointl_contr

It contracts a simple connect region and its boundary to a pointr_contr

Absorption operations ….

Merge, functions …….

It reduces a region and its boundary lines to a liner_thinning

Contract functions

3.2 Temporal Characteristics

The FE model, allows representing temporal

characteristics on different structures as factEntity,

hierarchical level, and attribute; which we called

Temporal FactEntity; Temporal Level and Temporal

Attribute respectively. We consider the temporal

characteristics called: Type of Time, Evolution and

Granularity. The Type of time: (TT) represents the

Transaction Time, (VT) represents the Valid Time

and (TVT) represents the combination of both. The

Evolution considers Specific evolution and

Historical evolution, the former only gathers the

new values, and the moment in which a change has

happened; the latter keeps all the values and

moments in which the changes have happened. A

A STUDY OF THE SPATIAL REPRESENTATION IN MULTIDIMENSIONAL MODELS

343

Granularity is one partition of a time domain chosen

to represent an event, and is the maximum update

frequency of an object or element.

3.3 Multigranularity Characteristics

We define the spatial multi-granularity as a spatial

characteristic that allows us to represent a space of

interest with different Semantic granularities, where

each Semantic granularity can have one or several

Geometric granularities different. The temporal

multi-granularity is a characteristic that allows us to

represent the changes of an element or group in

different temporal granularities. The spatio-temporal

multi-granularity allows us to represent a spatial

data with both: spatial multi-granularity and

temporal multi-granularity.

3.4 Elements

The FE model has two main concepts: dimension

and factEntities.

A factEntity contains only a fact, which is the

object of study and focus of analysis. A fact makes

up one or various measures. The dimensions are the

different perspectives under which we wish to

observe this fact. The FE model, allows an explicit

representation on the schema, of the functions that

are apply on hierarchical levels and measures when

is executed the Rollup, i.e, (the granularities

change). We see the graphical representation in

Figure1.

The FE model introduces the concept of

factEntity. A factEntity allows representing a fact

(by means of its measures) and its dimensions

associated. We distinguish two types of factEntities:

Basic and Virtual.

A Basic factEntity, is made up of basic data (the

identifiers of each leaf level of all dimensions and

basic measures); The Virtual factEntities are made

up of the “evolution” of basic data, when is done the

Rollup on one or various dimensions. Thus, a

Virtual factEntity contains the unfolded data of

some dimensions and derived measures. The derived

measures are the result of applying aggregation

functions on the measures of the basic factEntity.

See, Table 7 and Table 9.

Table 9: Spatial Functions.

User Defined

Equi-partition, nearest-neighbor indexHolistic

Center of n geometric points, center of gravityAlgebraic

Convex hull, geometric union, geometric intersectionDistributive

User Defined

Equi-partition, nearest-neighbor indexHolistic

Center of n geometric points, center of gravityAlgebraic

Convex hull, geometric union, geometric intersectionDistributive

The spatial data are relevant to this work when

they are included in a factEntity and they are

representative of dimensions or measures. The FE

model considers three types of hierarchies,

according to the implication that has the

“navigation” between its levels, on the basic

measures; these are Dynamic, Static and Hybrid. In

Dynamic hierarchy, the navigation between its

different levels implies changes in basic measures,

are suitable to represent the granularities of the

thematic dimensions, and the semantic granularities

of spatial data. In Static hierarchy, the navigation

between its different levels does not imply changes

in basic measures, and are appropriate to represent

the different geometric granularities of spatial data.

The Hybrid hierarchy is composed of a mixture of

the two previous types and allows us to represent a

spatial data with different and interrelated Semantic

and Geometric spatial granularities.

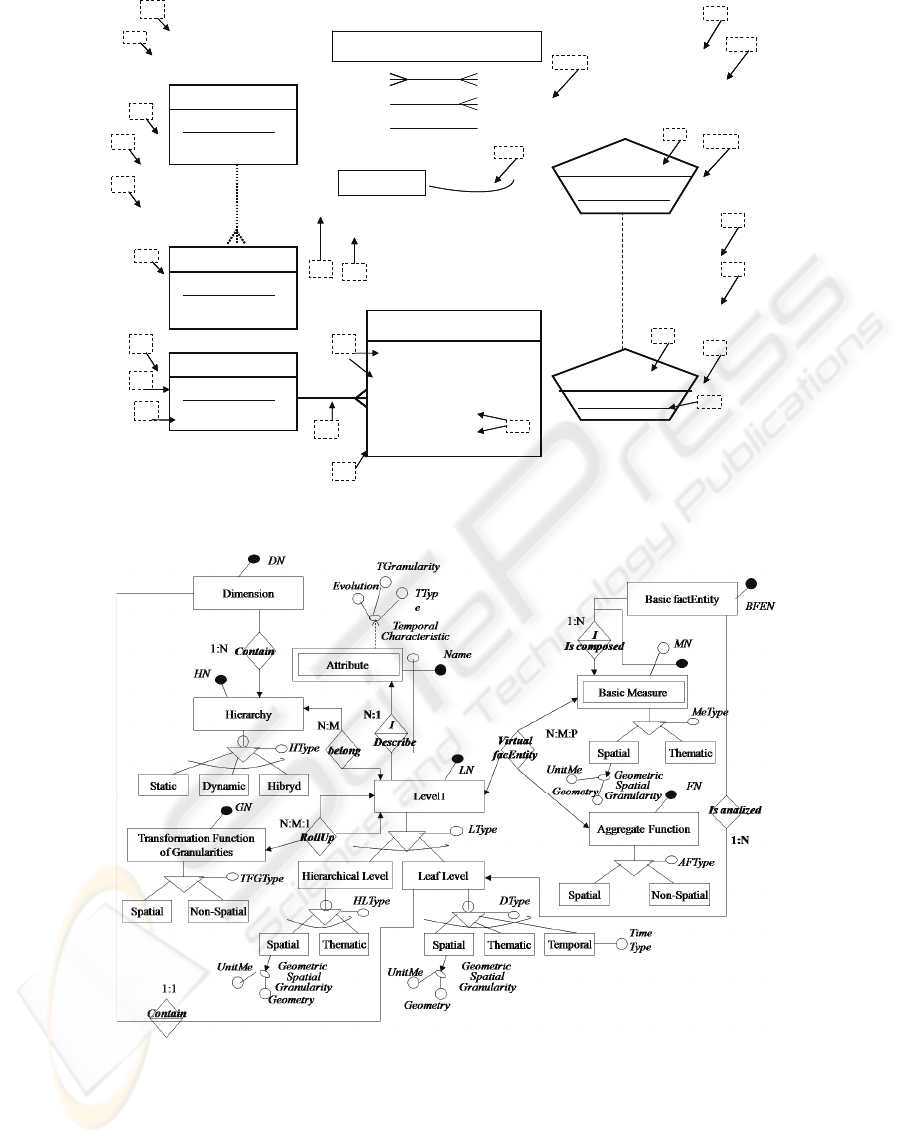
3.5 Graphical Presentation

The FE model proposes constructors to gather the

semantics of the multidimensional data models and

the spatio-temporal multigranularity. See Table 10,

and Figure 1.

Table 10: Explanations of FE model constructors.

p) Functions to reach a coarser granularity

between levels

m) Cardinalities: minimum and maximum

number of members related between two

consecutive levels

k) Basic FactEntity

h) Secondary attribute

e.2) Geometric spatial granularity

c) Leaf levela) Dimension name b) Hierarchy name

d) Level of Dynamic

Hierarchy

e.1) Level of Static Hierarchy

different from leaf level

f) Parent-child relation g) Primary attribute

i) Temporal attribute j) Attribute with historical evo lution

l.1) Basic Measures l.2) Primary attribute

n) Exclusivity

o) Functions applied on the

measures when Rollup is done

p) Functions to reach a coarser granularity

between levels

m) Cardinalities: minimum and maximum

number of members related between two

consecutive levels

k) Basic FactEntity

h) Secondary attribute

e.2) Geometric spatial granularity

c) Leaf levela) Dimension name b) Hierarchy name

d) Level of Dynamic

Hierarchy

e.1) Level of Static Hierarchy

different from leaf level

f) Parent-child relation g) Primary attribute

i) Temporal attribute j) Attribute with historical evo lution

l.1) Basic Measures l.2) Primary attribute

n) Exclusivity

o) Functions applied on the

measures when Rollup is done

3.6 A Metamodel of FE Model

We present the formalization of FE model with a

Metamodel made up with the extended ER model,

which represent the semantic of constructor of FE

model. See Figure 2.

4 EXAMPLE OF APPLICATION

We want to study “the evolution of riverbeds and

plots within a geographic area and in addition the

percentage of pollution that have these zones. These

data are analyzing each year. The rivers each five

years and the plot each two years, are checked.

Besides we desire have a history on the number of

inhabitants for Village, these data are gathering

once month. See Figure 3.

ICEIS 2008 - International Conference on Enterprise Information Systems

344

Leaf Level

Primary attribute/s

Secondary attribute

Conversion Function 1(Spatial data)

Granularity n Geometry n

Granularity 1 Geometry 1

Conversion Function n(Spatial data)

Basic FactEntity

Primary attribute (Dimension1)

-------------

Primary attribute (Dimensionn)

Basic Measure 1

…………

Basic Measure n

Leaf level

Primary attribute/s

Secondary attribute

Level L

Primary attribute/s

Secondary attribute

Level L

j+1

NameH Dynamic Hierarchy

NameH Static Hierarchy

NameD Dimension

Aggregate Function (Basic Measure n)

Binary Relationships

Tematic Level

Spatial Level

Cardinalities: 0,1; 0,n; 1,1; 1,n;

(0, n)/ (0, n)

Temporal attribute: Name(Granularty,Type)

Temporal Attribute with historical evolution:

<Name(Granularty,Type)>

Exclusivity

Primary attribute/s

Aggregate Function (Basic Measure1)

--------------- ------------

l.1

(0, 1)/ (1, 1)

(0, n)/ (1, n)

(0, 1)/ (1, 1)

l.2

Leaf Level

Primary attribute/s

Secondary attribute

Primary attribute/s

Secondary attribute

Conversion Function 1(Spatial data)

Granularity n Geometry n

Granularity 1 Geometry 1

Conversion Function n(Spatial data)

Basic FactEntity

Primary attribute (Dimension1)

-------------

Primary attribute (Dimensionn)

Basic Measure 1

…………

Basic Measure n

Leaf level

Primary attribute/s

Secondary attribute

Level L

Primary attribute/s

Secondary attribute

Primary attribute/s

Secondary attribute

Level L

Primary attribute/s

Secondary attribute

Level L

j+1

Primary attribute/s

Secondary attribute

Primary attribute/s

Secondary attribute

Level L

j+1

NameH Dynamic Hierarchy

NameH Static Hierarchy

NameD Dimension

Aggregate Function (Basic Measure n)

Binary Relationships

Tematic Level

Spatial Level

Cardinalities: 0,1; 0,n; 1,1; 1,n;

(0, n)/ (0, n)

Temporal attribute: Name(Granularty,Type)

Temporal Attribute with historical evolution:

<Name(Granularty,Type)>

Exclusivity

Primary attribute/s

Aggregate Function (Basic Measure1)

--------------- ------------

e1e1

l.1

e2e2

(0, 1)/ (1, 1)

(0, n)/ (1, n)

(0, 1)/ (1, 1)

l.2

Figure 1: Notations to FE Conceptual Multidimensional Model.

Figure 2: Metamodel of FE model, made up with the ER model.

This is an example with temporal characteristic

in factEntity, hierarchical level, and attribute and

multiple spatial and temporal granularities

interacting.

5 CONCLUSIONS

This work has presented a study on the one of some

models proposed to model multidimensional

databases, and on the other one, of models that

includes spatial data. We have also seen that most

A STUDY OF THE SPATIAL REPRESENTATION IN MULTIDIMENSIONAL MODELS

345

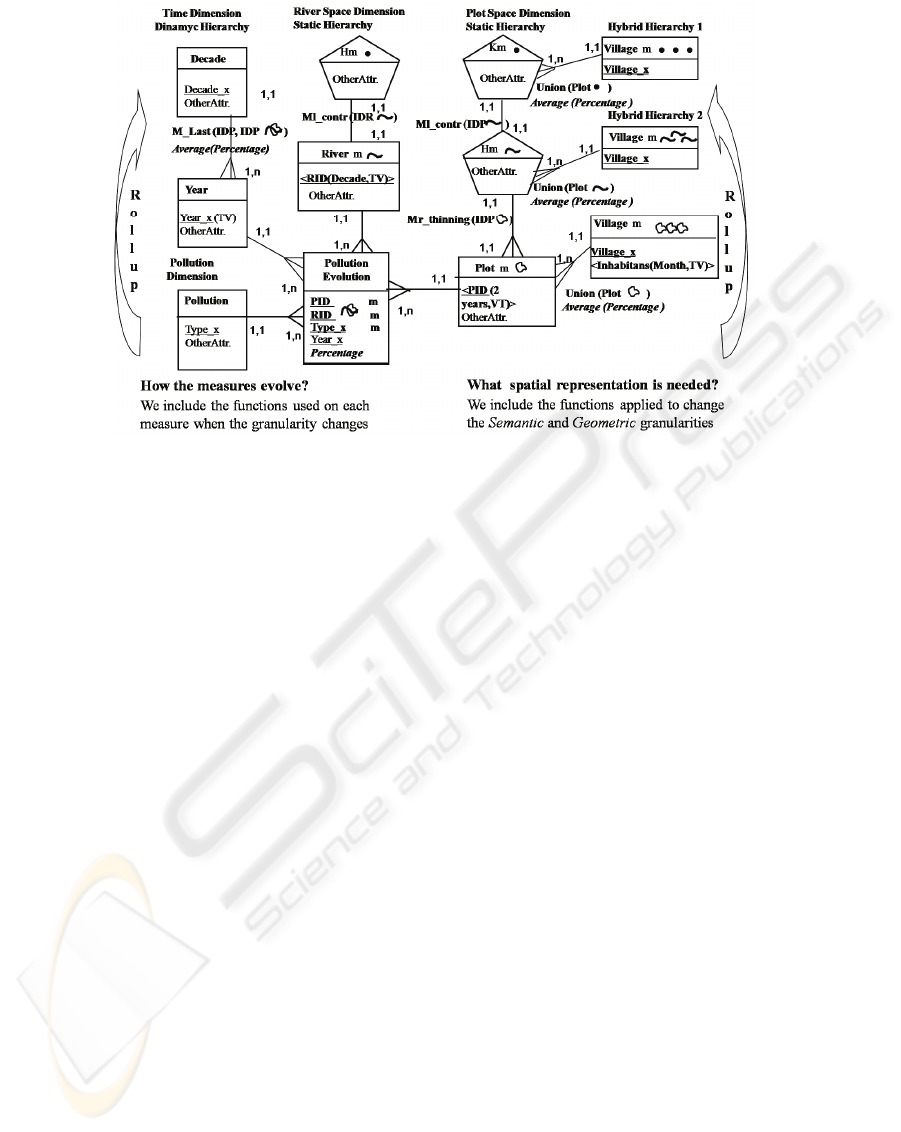
Figure 3: Example with different and related Spatial and Temporal granularities.

models reuse the conventional models of database

design, to deal these two semantics. However, we

have shown that they are fully adequate to pick up

spatial and multidimensional semantics. In addition,

we have proved that the analyzed models not reflect

these two semantics together. We have made up a

comparison between some more relevant models and

the FE model proposed in our previous works, and

we are shown that the models studied are not gather

the multidimensional and spatial characteristics as

the FE model does, highlighting the Semantic and

Geometric spatial granularities, these, are not

distinguished by neither of analyzed models. We

emphasize on the novel contributions of our FE

model to handle the spatial component and

shortcomings of the rest of model compared. We

have propose to add into the characteristics that a

conceptual multidimensional model should to

gather, some rules as need to handle spatial

characteristic as are the spatial and temporal

multigranularities. We analyze how to divide a space

of interest for semantic characteristics and as to

represent this in a database, with different form and

size. In addition, we have presented a Metamodel

that gather the semantic of the FE model, made up

with the ER model. Finally, we analyze an example

of application where we expose explicitly how to

represent the Semantic and Geometric spatial

granularities interrelated, using as framework the FE

model.

We emphasize on the utility of that the

models support the spatio-temporal

multigranularities semantics, as the FE model does.

In the near future, we make up the formal definition

of FE model with logical formulas and BNF

grammars. We intend to study specific constraints

for space and time in order to maintain the

consistency between all objects of the database. We

are considering making up a case tool that support

the FE model and enable us to transform our

conceptual model into models that are closer to the

implementation of databases.

ACKNOWLEDGEMENTS

We are grateful ICEIS 2008 Conferences for its

kindness and the reviewer of this paper for their

recommendations.

REFERENCES

Abello A., Samos J., Saltor F., 2000. A Data Warehouse

Multidimensional Models Classification. Technical

Report LSI-2000-6. (Universidad de Granada).

Abelló A., Samos J., Saltor F., 2002. YAM2 (Yet Another

Multidimensional Model): An extension of UML. In

Proc. of the Int. DB Engineering and Application

Symposium, pp. 172-181.

Abelló A., Samos J., Saltor F., 2006. YAM2, a

multidimensional conceptual model extending UML.

Information Systems, Vol. 31, No. 6. pp. 541-567.

Blaschaka M., Sapia C., Höfling G., Dintel B., 1998.

Finding your way through multidimensional data

models. In 9th Int. Conf. on Database and Expert

ICEIS 2008 - International Conference on Enterprise Information Systems

346

Systems Applicactions (DEXA). Lecture Notes in

Computer Science 1460, Springer-Verlag, pag 198-

203.

Bedard Y., 1999. Visual modeling of spatial databases:

towards spatial PVL and UML. Geomantic 53 (2),

169-186.

Bedard Y., Bernier E., 2002. Supporting Multiple

Representations with Spatial Databases Views

Management and the concept of VUEL. Proc. of the

Joint Workshop on Multi-Scale Representations of

Spatial Data, ISPRS.

Berloto M., 1998. Geometric Modeling of Spatial Entities

at Multiple Levels of Resolution. PhD Thesis, Uni.

degli Studi di Genova.

Bettini, C., Jajodia, S. & Wang, S., 2000. Time

Granularities in Databases, Data Mining and Temporal

Reasoning. Ed. Springer-Verlag, New York, Inc.

Secaucus, NJ, USA.

Borges, K. A. V., Davis Jr C.A., Laender A. H. F. 2001.

OMT-G: An object-oriented data model for

geographic applications. Geo Informatics 5 (3), 221-

260.

Camossi, E., Bertolotto M., Bertino E., Guerrini G., ,

2003. ST_ODMG: A Multigranular Spatiotemporal

Extension of ODMG Model. Technical Report DISI-

TR-03-09, Università degli Studi di Genova.

Camossi E., Bertolotto M., Bertino E., Guerrini G., 2003.

A Multigranular Spactiotemporal Data Model. Proc.

of the 11th ACM international symposium, Advances

in GIS, pp: 94-101. New Orleans. USA.

Gascueña C. M., Moreno L., Cuadra D., 2005. Dos

Perspectivas para la Representación de la Multi-

Granularidad en Bases de Datos Espacio-Temporales.

IADIS 2005 conferences.

Gascueña C. M., Cuadra D., Martínez P., 2006. A

Multidimensional Approach to the Representation of

the Spatiotemporal Multigranularity. Proc. of the 8th

International Conference on Enterprise Information

Systems, ICEIS 2006.Cyprus.

Gascueña C. M., Guadalupe Rafael, 2008. Some Types of

Spatio-Temporal Granularities in a Conceptual

Multidimensional Model. 7th International

Conference , APLIMAT Bratislava, Slovak.

Gascueña C. M., Guadalupe Rafael, 2008. Some Types of

Spatio-Temporal Granularities in a Conceptual

Multidimensional Model. Aplimat -Journal of Applied

Mathematics, volume 1 (2008), number 2, pag: 215-

216.

Golfarelli M., Mario D., Rizzi S., 1998. The dimensional

fact model: a conceptual model for data warehouses.

(IJCIS) 7 (2–3) pp: 215–247.

Jones C.B., Kidner D.B., Luo L.Q., Bundy G.L., Ware

J.M., 1996. Databases design for a multi-scale spatial

information system. Int. J., GIS 10 (8) pg 901-920,.

Khatri V., Ram S., Snodgrass R. T.,. 2006. On

Augmenting database design-support environments to

capture the geo-spatio-temporal data semantics, 2004,

Publisher Elsevier Science Ltd, Volume 31, Issue 2

2006, Pages: 98 - 133.

Kimball R., 1996. The Data Warehouse Toolkit. John

Wiley&Sons Ed.

Le, Y., 2005. A prototype temporal GIS for multiple

spatio-temporal representations. Cartography and GIS

Science, 32(4), 315-329.

Luján-Mora S., Trujillo J., Song Il- Yeol., 2006. A UML

profile for multidimensional modeling in data

warehouses. DKE, 59(3), p. 725–769.

Malinowski, E. and Zimanyi, E., 2004. Representing

Spatiality in a Conceptual Multidimensional Model.

Proc. of the 12th annual ACM international workshop

on GIS. Washington, DC, USA.

Malinowski E., Zimanyi E. , 2004. OLAP hierarchies: A

conceptual perspective. In Proc. of the 16th Int. Conf.

on Advanced Information Systems Engineering, pages

477-49.

Malinowski E., Zimanyi E., 2005. Spatial Hierarchies and

Topological Relationships in the Spatial MultiDimER

model. Lecture Notes in Computer Science, page 17,

Volume 3567.

Malinowski E., Zimanyi E., 2006. Inclusion of Time-

Varying Measures in Temporal Data Warehouses

dimensions. Proc. of 8th International Conference on

Enterprise Information Systems, Paphos, Cyprus.

Malinowski E., Zimanyi E., 2006. A Conceptual Solution

for Representing Time in Data Warehouse

Dimensions. Proc. of 3rd Asia-Pacific (APCCM2006),

Hobart, Australia.

Parent C., Spaccapietra S., Zimanyi E., 1999. Spatio-

temporal conceptual models: Data

structures+space+time. Proc. of 7th ACM Symposium

on Advances in Geographic Information Systems,

Kansas City, USA, pp.

Parent C., Spaccapietra S., Zimanyi E., 2005. The

MurMur project: Modeling and querying multi-

representation spatio-temporal databases, in press

Elsevier ltd.

Parent C., Spaccapietra S., Zimanyi E., 2006. The

MurMur project: Modeling and querying multi-

representation spatio-temporal databases. Information

Systems, Volume 31, Issue 8, Pages 733-769.

Pedersen T., 2000. Aspects of Data Modeling and Query

Processing for Complex Multidimensional Data. PhD

thesis, Faculty of Engineering & Science, Aalborg

University.

Piattini Mario G., Esperanza Marcos, Coral Calero, Belén

Vela, Tecnología y Diseño de Bases de Datos,

Editorial: Ra-Ma 2006.

Sapia C., Blaschka M., Höfling G., Dinter B., 1999.

Extending the E/R Model for the Multidimensional

Paradigm. Advances in DB Technologies. LNCS Vol

1552, Springer-Verlag.

Stefanovic, N. Han, J. and Koperski, K., 2000. Object-

based selective materialization for efficient

implementation of spatial data cubes. IEEE Trans. on

Knowledge and Data Engineering, 12(6):938-958.

Stell J., Worboys M., 1998. Stratified map spaces: a

formal basic for multi-resolution spatial databases.

Proc. of the 8

International Symposium on Spatial

Data Handling, SDH’98 pag 180-189.

A STUDY OF THE SPATIAL REPRESENTATION IN MULTIDIMENSIONAL MODELS

347

Timpf S., 1999. Abstraction, level of detail, and

hierarchies in map series. International Conference on

Spatial Information Theory, COSIT’99, LNCS 1661,

pp. 125-140.

Torlone R., 2001. Conceptual Multidimensional Models.

In Rafanelli ed., pages 69-90.

Torlone R. 2003. Conceptual Multidimensional Models. In

Multidimensional databases: problems and solutions,

Idea Group Publishing, Hershey, PA, pages 69-90,

USA,

Tryfona N., Busborg F., Borch J. , , 1999. StarER: A

Conceptual Model for Data Warehouse Design. In

Proc. of the 2nd ACM Int. Workshop on DW and

OLAP, pp. 3-8.

Tryfona, N., Price, R., & Jensen, C. S., . 2003. Conceptual

Models for Spatio-temporal Applications. In M.

Koubarakis et al. (Eds.), Spatio-Temporal DB: The

CHOROCHRONOS Approach (pp. 79-116). Berlin,

Heidelberg.

Vargas da Rocha L., Edelweiss L. V., Iochpe C. , 2001.

GeoFrame-T: A temporal conceptual framework for

data modeling. Proceedings of the ninth ACM

international symposium on Advances in GIS, Atlanta,

GA, USA.

William A. Mackaness., 2006. Automated Cartography in

a Busch of Ghosts. Cartography and GIS Science,

Volume 33, Nº 4.

ICEIS 2008 - International Conference on Enterprise Information Systems

348