A DECISION SUPPORT SYSTEM FOR INTEGRATED

ASSEMBLY AND DISASSEMBLY PLANNING USING A GA

APPROACH

Yuan-Jye Tseng, Hsiao-Ting Kao and Feng-Yi Huang

Department of Industrial Engineering and Management, Yuan Ze University

135 Yuan-Tung Road, Chung-Li, Taoyuan 320, Taiwan

Keywords: Decision support system, Product life cycle management, Assembly planning; Disassembly planning.

Abstract: In a decision support system for a complete product life cycle management, both assembly planning and

disassembly planning need to be considered for producing an assembled product. To produce an assembled

product, an assembly planning scheme is required to generate a proper assembly sequence with which the

components can be grouped and fixed to construct a final product. At the end of the product life cycle, a

disassembly planning scheme is performed to generate a disassembly sequence to disassemble and recycle

the product. In this research, a new decision support system for a complete product life cycle management

by integrating assembly and disassembly planning is presented. First, the spatial relationships of the

components and the precedence of the assembly and disassembly operations are analyzed. Second, a

genetic algorithm approach is applied to evaluate the integrated assembly and disassembly costs to find the

good assembly sequences and disassembly sequences. A cost function by integrating the assembly costs

and disassembly costs is formulated and used as an objective function. An example product is demonstrated

and discussed. The test result shows that the decision support system is feasible and effective for

integrating assembly and disassembly planning with a complete product life cycle management.

1 INTRODUCTION

In a complete product life cycle management system

of an assembled product, both an assembly sequence

and a disassembly sequence are required. An

assembly sequence is required to produce a new

product by applying a series of assembly operations

on a group of components at the start of the life

cycle. A disassembly sequence is needed to

decompose the product into disposable or recyclable

parts or components by applying a series of

disassembly operations at the end of the life cycle.

The main purpose of assembly planning (assembly

sequence planning) is to arrange a proper assembly

sequence with which the components can be

grouped and fixed together to build a final product.

The assembly sequence can be defined as an ordered

sequence of assembly operations required to produce

a product. On the other hand, the purpose of

disassembly planning (disassembly sequence

planning) is to arrange a disassembly sequence with

an ordered disassembly operations for disassemble a

product. Therefore, in a decision support system for

a complete product life cycle management, both the

assembly planning and disassembly planning need to

be considered and integrated.

In the traditional way, the assembly planning

models and the disassembly planning models are

performed as two independent tasks. As a result, the

two planning models are executed separated without

interaction. Therefore, a good assembly sequence

may sometimes contradict the considerations in the

disassembly planning model. In addition, a good

disassembly sequence may not support the

requirements in the corresponding assembly

planning model. Given a set of components, a good

assembly sequence can be planned by considering

the contact and spatial relationships between the

components. A series of assembly operations need

to be determined by analyzing the contact and

spatial relationships between components. Once the

assembly operations are determined, the assembly

operations need to be ordered in sequence by

evaluating the required cost objective in the

assembly planning model. In the traditional

planning scheme, the cost objective considers only

348

Tseng Y., Kao H. and Huang F. (2008).

A DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY PLANNING USING A GA APPROACH.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 348-355

DOI: 10.5220/0001717203480355

 SciTePress

the assembly costs occurred in the assembly

planning scheme.

Traditionally, the assembly sequence is

determined by evaluating the assembly cost

objective. In this case, although a low assembly cost

can be achieved, it may cost more to disassemble the

product at the end of the product life cycle. The key

issue is that an assembly operation with a low cost

may not correspond to a disassembly operation with

the same low cost. In some cases, if a relatively low

cost is used for fixing the two specific components,

it may require a higher cost to perform the

corresponding disassembly operation for separating

the two components. As a result, an assembly

sequence with a low cost may result in a

disassembly sequence with a high cost for the same

product at the end of the product life cycle.

Therefore, a complete decision support system

must include both assembly planning and

disassembly planning. To deal with the special

characteristics of a complete product life cycle,

organizing and sequencing of assembly and

disassembly operations must be considered

concurrently in order to generate an integrated

sequence.

In the related research for assembly planning, it

can be summarized that assembly planning can be

performed in three stages: (1) assembly modelling

and representation, (2) assembly sequence

generation, and (3) assembly evaluation and

optimization. A recent review can be found in

Abdullah et al. (2003). The previous research in

assembly planning can be classified into three

categories. The first category uses rules or

knowledge bases to perform generation of different

assembly sequences such as developed in DeFazio

and Whitney (1987), Heemskerk and Van Luttervelt

(1989), Ye and Urzi (1996), and Swaminathan and

Barber (1996). The second category presents

automatic generation of feasible assembly

sequences using graph representation forms

including the research presented in de Mello and

Sanderson (1991), Santochi and Dini (1992), Lin

and Chang (1993), and Choi et al (1998). The third

category focuses on assembly analysis and

evaluation for searching the better or the optimal

assembly sequence. The research in this class

includes de Mello and Sanderson (1991), Ben-

Arieh, and Kramer (1994), Laperriere and

ElMaraghy (1996), Gottipolu and Ghosh (1997),

Tseng and Liou (2000), and Chen et al. (2004).

With a given set of components, sequencing a

given set of components may become a

combinatorial problem with an explosive number of

potential sequences. From a mathematical point of

view, this is an NP-hard problem with the number of

assembly and disassembly sequences proportional to

the factorial of number of components. From the

solution aspect, genetic algorithms (GAs) have been

proven to be effective and efficient in solving NP-

hard problems such as TSP (traveling salesman

problem). In the research by De Lit et al. (2001),

Chen et al. (2002), Marian et al. (2003), Li et al.

(2003), and Smith (2004), GA method has been

applied to find solutions in assembly planning

models.

In this research, a decision support system for a

complete life cycle management by integrating

assembly and disassembly planning is presented.

First, two graph-based models called assembly

precedence diagram and disassembly precedence

diagram are presented to represent the spatial

relationships of the components and the associated

precedence relationships of assembly and

disassembly operations. Next, two precedence

matrices called assembly precedence matrix and

disassembly precedence matrix are built for

checking the feasible sequences. Finally, several

operation cost functions are developed to evaluate

the costs of the integrated assembly and disassembly

sequences. A method using the genetic algorithm

(GA) approach is developed for finding the solutions

with an objective of minimizing the costs.

In this paper, section 2 presents the graph-based

representation models for integrating assembly and

disassembly planning. Section 3 discusses the cost

functions for evaluating the sequences. Section 4

presents a GA method for finding the solutions.

Section 5 discusses the test results with an example.

Finally, section 6 concludes this study.

2 REPRESENTATION MODELS

The input of the decision support system includes

the definitions of the components, the spatial

relationships of the components, the available

assembly and disassembly operations, and the

associated assembly and disassembly costs. Two

graph-based models are presented to represent the

integrated assembly and disassembly sequences.

The graph-based models can be summarized as

follows.

(1) Assembly precedence diagram (APD),

(2) Disassembly precedence diagram (DPD).

An assembly precedence diagram (APD) is a

directed graph showing the precedence of the

components and the associated assembly operations

(Lin and Chang, 1993). In this research, the concept

of APD is applied to represent the spatial

connectivity relationship and precedence between

A DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY PLANNING USING A GA

APPROACH

349

two components. To assemble a group of

components with collision-free assembly operations,

a proper precedence is specified in the APD. In this

research, the concept is expanded for use in

disassembly planning by defining the disassembly

precedence diagram (DPD). An example product A

is shown in Figure 1. The APD and DPD of the

product A are shown in Figure 2 and Figure 3.

In order to analyze and evaluate the feasible

sequences, the two graph-based models of APD and

DPD are transformed into two matrix forms. The

concept of matrix form has been introduced by

Santochi and Dini (1992) for representing the

precedence relationship between a pair of

components. In this research, the two new matrices

forms, assembly precedence matrix (APM) and

disassembly precedence matrix (DPM), are

developed for integrated assembly planning and

disassembly planning. The two matrix models for

the example product A is shown as follows.

APM =

⎥

⎦

⎤

⎢

⎣

⎡

nnnn

j-nj-j-

ppp

MMM

2221

12111

DPM =

⎥

⎦

⎤

⎢

⎣

⎡

nnnn

j-nj-j-

ppp

MMM

2221

12111

where p

and p

are components,

a value of p

= 0 represents that there is no

precedence between two components p

and p

a value of p

= 1 represents that there is

precedence between two components p

and p

Figure 1: Graphical illustration of the example product A.

Figure 2: The assembly precedence diagram APD of the

example product A.

Figure 3: The disassembly precedence diagram DPD of

the example product A.

3 COST FUNCTIONS

In the presented decision support system, the related

assembly and disassembly costs are identified and

modelled. The operation cost functions (OCFs)

define the operation costs required in an integrated

assembly and disassembly sequence. The operation

cost functions include two types of costs, assembly

costs and disassembly costs. A cost function by

integrating the assembly costs and disassembly costs

is formulated and used as an objective function. The

assembly costs include assembly operation cost,

assembly instability cost, assembly accessibility

cost, assembly tool setup cost, and assembly weight

effect cost. The disassembly costs include

disassembly operation cost, disassembly instability

cost, disassembly accessibility cost, disassembly tool

setup cost, and disassembly weight effect cost.

The cost items are described as follows.

(1) Assembly operation cost (ACC): To complete

the assembly operations, proper operation cost

is required. The assembly operation cost is the

basic operational cost for performing an

assembly operation.

(2) Disassembly operation cost (DCC): To

complete the disassembly operations, proper

operation cost is required. The disassembly

operation cost is the basic operational cost for

performing a disassembly operation.

(3) Assembly instability cost (SC): The instability

cost is used to describe the cost for maintaining

ICEIS 2008 - International Conference on Enterprise Information Systems

350

the stability of the components and the

assembled product in the assembly operations.

(4) Disassembly instability cost (USC): instability

cost is used to describe the cost for maintaining

the stability of the product and the

disassembled components in the disassembly

operations.

(5) Assembly and disassembly accessibility cost

(ADC and DDC): The accessibility cost is used

to describe the degree of difficulty in accessing

the parts to complete the assembly operations

(ADC) or disassembly operations (DDC).

(6) Assembly and disassembly tool setup cost

(ATC and DTC): To perform the assembly

operations, proper tools and tool setups are

required (ATC). To perform the disassembly

operations, proper tools and tool setups are

required (DTC).

(7) Assembly and disassembly weight effect cost

(WAI and WDI): To complete the assembly

operations and the disassembly operations, the

components and subassemblies need to be

moved to different orientations or different

positions. Therefore, proper weight effect cost

for moving and handling needs to be defined

for assembly operations (WAI) and disassembly

operations (WDI).

The value of each of the cost functions is

measured on a consistent scale with proper

weighting factors. Given a feasible sequence and the

associated assembly and disassembly information,

the required cost values can be calculated and

evaluated with a consistent unit in dollars. In

practice, the data of each cost function can be

evaluated and recorded according to the information

and the formulations set by the manufacturing plant.

The numerical data of each cost item can be

recorded in a knowledge base and can be checked

using a table format in the process for evaluating a

feasible sequence. The summation of the cost items

is performed using a consistent cost scale. The total

cost function (TC) is the sum of all the operation

cost functions and can be described using the

following equation:

TC = (ACC+SC+ADC+ATC+WAI) +

(DCC+USC+DDC+DTC+WDI ) (1)

4 SOLUTION USING GENETIC

ALGORITHM

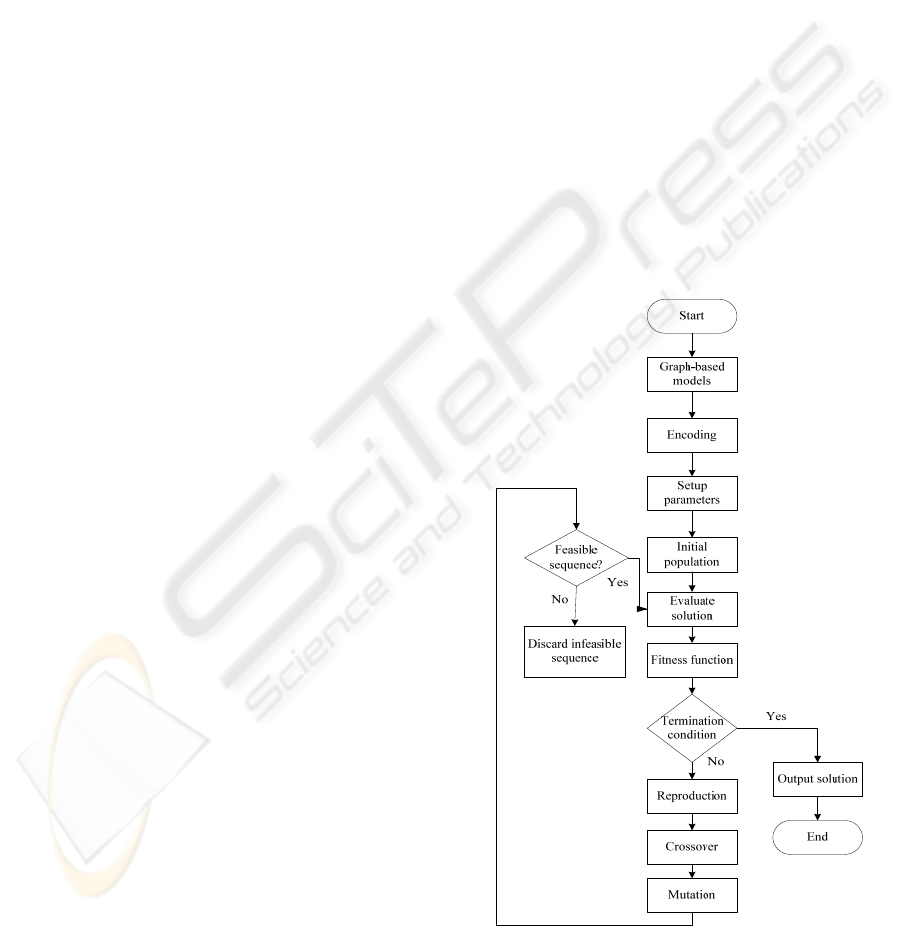
4.1 Overall Flow

In the decision support system, the GA approach is

applied to evaluate costs of the integrated sequences

and find the good solutions. The input includes the

definitions of the product and components and the

APD, DPD, APM, and DPM information. The

overall flow of the GA method is illustrated in

Figure 4. First, a new encoding scheme is

developed for representing the integrated assembly

and disassembly sequence. The ordered list of

components is encoded as a chromosome. The

fitness function is defined using the total cost (TC)

of the operation cost functions (OCF). To run the

GA method, an initial population is given first. The

operators of genetic algorithms are performed to

find the solutions. The output sequence is

represented using the ordered components and

operations. The final output of the decision support

system represents the integrated assembly and

disassembly sequence for producing the product.

The GA starts with an initial population and the

population evolves at each generation. An

evaluation is performed to find the chromosome

with a high fitness value to replace the chromosome

with a low fitness value.

Figure 4: The overall flowchart of the GA method.

A DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY PLANNING USING A GA

APPROACH

351

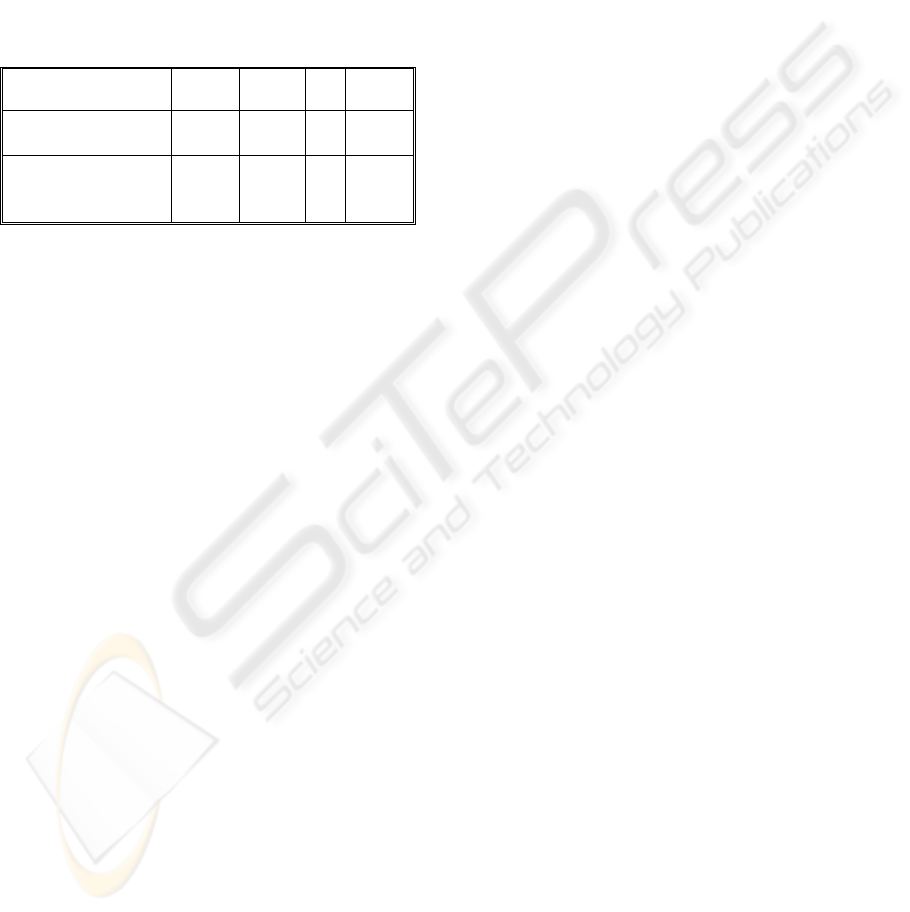
4.2 Encoding

In the GA method, a sequence represented by an

ordered list of components and operations and is

used in the chromosome encoding format. In the

genetic algorithm approach, the populations are

represented by the codes of chromosomes. The

format of the encoded chromosome is shown in

Table 1.

Table 1: The encoding format of a chromosome

representation of an integrated assembly and disassembly

sequence.

Component Name

1 2

…

Operation Number

(OP)

OP(1) OP(2)

…

OP(n)

Operation Type:

Assembly (A)

Disassembly (D)

A A

…

Component name denotes the name of a

component. The operation number is an indexed

number of the operation performed on the

component. The operation type includes assembly

operation (A) and disassembly operation (D). The

encoded chromosome represents a list of sequenced

components. The validity of a chromosome for

representing a feasible sequence can be checked

from the APD and APM for assembly sequences,

and DPD and DPM for disassembly sequences.

4.3 Setup Parameters and Fitness

Functions

The parameters used in the genetic algorithms are

defined as follows.

(1) P

Size

: the population size defining the number of

chromosomes in the populations, with a setup

value of 10,

(2) C

Method

: the crossover method, partially mapped

crossover, cycle crossover, and order

crossover can be applied,

(3) C

Rate

: the crossover rate, with an initial value of

0.7,

(4) M

Rate

: the mutation rate, with an initial value of

0.3,

(5) G

Number

: the generation number representing the

condition that the computation stops, with a

setup value of 100.

The fitness function is used to evaluate the

chromosomes and to make choices leading to a good

solution. The decision making of a good solution is

made according to the fitness function. The fitness

function of the integrated assembly and machining

sequences can be derived from the OCF. The fitness

function fit(i) can be defined as follows. The

objective is to find a good sequence by minimizing

the OCF. In the GA method, a chromosome with a

lowest fitness value is chosen to the next generation.

fit(i) = OCF(i), (2)

fit(i): the fitness function value of chromosome i,

OCF(i): the operation cost of chromosome i.

4.4 Solution with GA Method

The step-by-step GA method for finding solutions is

described as follows.

Step 1. Initialization.

(1) Define the chromosome representation

format.

(2) Encode the chromosome.

(3) Determine the population size, the

probability for crossover, the

probability for mutation.

Step 2. Initial population.

(1) Initialize the chromosome index

number i = 1.

(2) Generate a feasible sequence from the

APD.

(3) Encode the ordered entities to model a

chromosome i.

(4) i = i + 1, until i > P

Size

Step 3. Evaluation of fitness function value.

The objective of fitness function can be

represented as shown in formulation (2).

The fitness function value is calculated for

each feasible sequence.

Step 4. Reproduction.

In reproduction operator, the fitness value of

a chromosome is used for making decision

for copying to the next generation. The

fitness value of each chromosome and the

total fitness of the population are calculated.

The reproduction probability for each

chromosome and the cumulative

reproduction probability for each

chromosome are calculated. The best

chromosome with the lowest fitness value is

chosen to the next generation.

Step 5. Crossover.

Crossover combines the elements from two

parent solutions to create new solutions. The

crossover operator is performed by splitting,

exchanging, and recombining the elements

from two parent chromosomes to create new

solutions in the next generation. Based on

different splitting, exchanging, and

ICEIS 2008 - International Conference on Enterprise Information Systems

352

recombining methods, different types of

crossover methods can be used.

Step 6. Mutation.

Mutation operator is used to increase the

population variety by randomly selecting

and replacing elements between two

chromosomes. In the exchanging method,

two elements in the two selected

chromosomes are chosen randomly and

exchanged. In the inserting method, an

element is chosen randomly and shifted a

random number of ordered positions to the

right or to the left. In this step, the

reciprocal exchange mutation is used. The

mutation number can be calculated as

Number

) = (M

Rate

) × (P

Size

Step 7. Evaluation of the solution.

By checking the APM and the DPM, if a

solution is not feasible, then it will be

discarded. If a sequence is not feasible, the

ordered operations of components will be

changed to a feasible sequence without

violating the precedence. The feasible

solutions and the fitness values are collected

and recorded.

Step 8. Termination condition.

Repeat step 3 to step 7 and C

Time

+1,

If (C

Time

Number

), the computation stops.

Step 9. Output solution with the best fitness value.

The evolution stops when the generation

number

Number

is reached. Finally, the

method outputs the solution with the best

fitness value.

5 IMPLEMENTATION AND TEST

RESULTS

In the presented decision support system, the models

were implemented and tested by developing

software on a personal computer. The input data

includes the product definition, the component

definition, the assembly operations and disassembly

operations information, and the cost information.

With the given product and component

definition, the geometric data is processed to

generate spatial and contact information between the

components. With the spatial and contact

information between components, the corresponding

APD and DPD and can be build. The matrix forms

APM and DPM can be calculated from the APD and

DPD.

Using the constructed graph-based models and

matrix forms, the feasibility of the integrated

assembly and disassembly sequences can be

examined. Next, the GA method is applied to find

the solutions. The example product A is illustrated

and discussed in this section. The example product

A is shown in Figure 1. There are 7 components, a,

b, c, d, e, f, and g. The APD and DPD is shown in

Figure 2 and Figure 3. The APM and DPM for the

example product A is shown in the following forms.

PM =

⎥

⎦

⎤

⎢

⎣

⎡

0100001

0000001

0000011

0000111

0000011

0000001

0000000

gfedcba

DPM

⎥

⎦

⎤

⎢

⎣

⎡

0000000

1000000

0000000

0001000

1011100

1111110

gfedcba

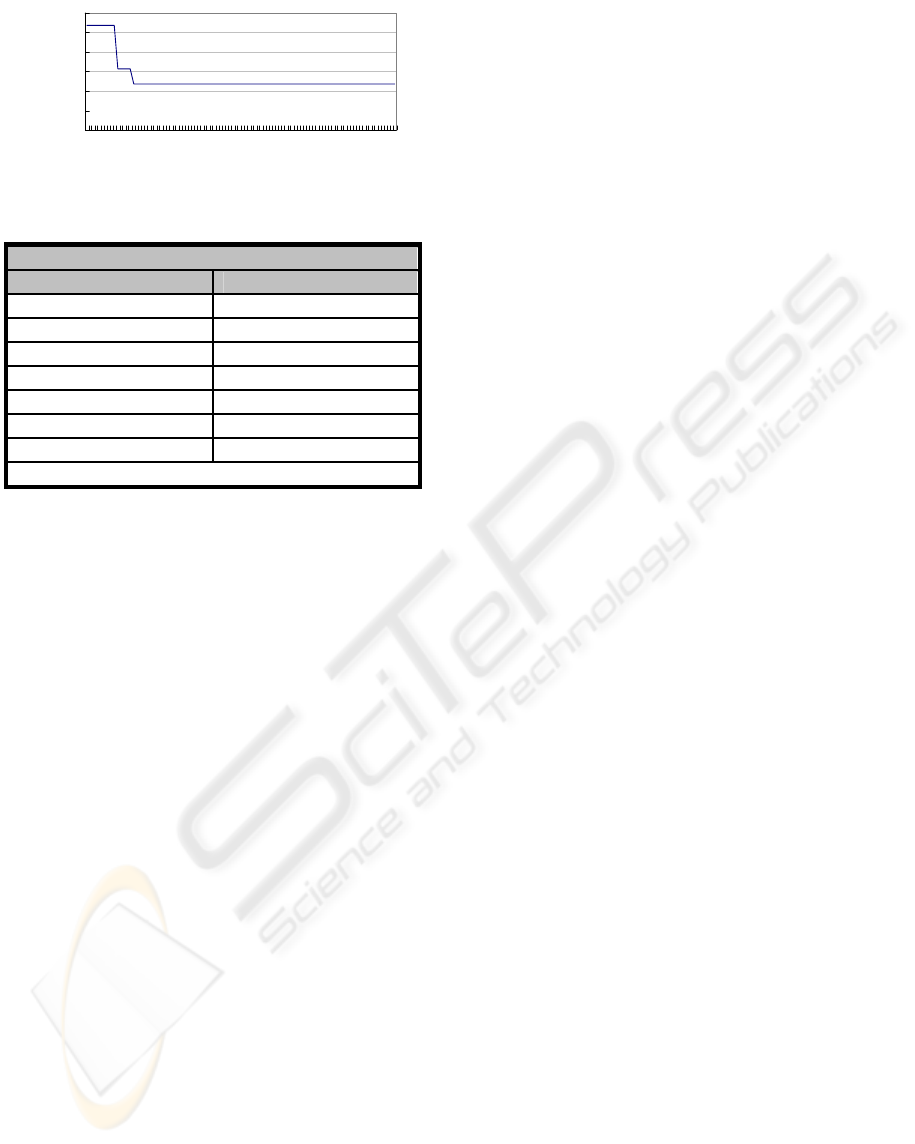
Finally, the GA algorithm is applied for finding

solutions. The test result of the GA method is

shown in Figure 5. Figure 5 shows that the

computation converges after 15 generations with the

near optimized low cost of $369.701. The solution

of the integrated assembly and disassembly

sequence is shown in Figure 6. Figure 6 describes

that the 7 components can be assembled and

disassembled with the described integrated assembly

and disassembly sequences with a near optimized

low cost. The For example, in the integrated

sequence 1, a→b→f→c→d→g→e represents the

assembly sequence, and g→e→d→c→f→b→a

represents the disassembly sequence.

It is observed that the combinatorial number of

sequences increases as the component number

grows. A larger number of components of the

product may lead to a longer computational time. It

can be concluded in general, if the component

number grows, the advantage of the GA method may

be highlighted with a comparatively shorter

computational time. Although the presented

methods can be useful for generating and evaluating

feasible sequences with good solutions, much

remains to be done to manage complicated products

with a large number of components.

A DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY PLANNING USING A GA

APPROACH

353

392

394

396

398

400

402

404

1 9 17 25 33 41 49 57 65 73 81 89 97

世代數

Figure 5: The test result of the GA method.

Integrated sequences

Assembly sequence Disassembly sequence

a→b→f→c→d→g→e g→e→d→c→f→b→a

a→b→e→f→c→d→g g→e→d→c→b→f→a

a→b→e→f→c→d→g g→d→c→e→f→b→a

a→b→e→f→c→d→g g→d→c→f→e→b→a

a→b→e→c→f→d→g g→e→d→c→f→b→a

a→b→e→f→c→d→g g→d→e→c→f→b→a

Cost = 194.64 Cost = 202.061

Integrated cost = 369.701

Figure 6: The test results of the integrated assembly and

disassembly sequences with the GA method.

6 CONCLUSIONS

In a complete decision support system for product

life cycle management of assembled products, both

the assembly and disassembly sequences need to be

planned. In a complete product life cycle of a

product, an assembly sequence is required to

produce a new product at the start and a disassembly

sequence is needed at the end to decompose and

recycle the product. In this research, the assembly

planning model and the disassembly planning model

are integrated to generated integrated assembly and

disassembly sequences. First, an assembly

precedence diagram (APD) and a disassembly

precedence diagram (DPD) are built by analyzing

the spatial relationships of the components and the

operations. The precedence relationships are

represented as assembly precedence matrix (APM)

and disassembly precedence matrix (DPM) for

checking feasibility of the generated sequences.

Second, a solution method using a GA approach is

applied to search for the good assembly sequence

and disassembly sequence. A cost function by

integrating the assembly costs and disassembly costs

is formulated. Example products are modeled and

tested. The final output of the decision support

system presents solutions of assembly sequences

and disassembly sequences. The test results show

that the GA method converges within a small

number of generations with a near optimized low

cost. It can be generally concluded that the

developed model in the decision support system is

feasible and effective for integrating assembly

planning and disassembly planning. The decision

support system is capable of finding complete

assembly and disassembly sequences with a near

optimized low cost. Further research should be

concerned with different genetic operators.

Moreover, more detailed assembly and disassembly

decision support factors and other related cost

functions can be further explored.

REFERENCES

Abdullah, T. A., Popplewell, K., and Page, C. J. (2003). A

review of the support tools for the process of assembly

method selection and assembly planning, International

Journal of Production Research, 41(11), pp. 2391–

2410.

Ben-Arieh, D., and Kramer, B. (1994). Computer-aided

process planning for assembly: generation of assembly

operations sequence, International Journal of

Production Research, 32(3), pp. 643-656.

Chen, R. S., Lu, K.-Y. , and Tai, P. H. (2004). Optimizing

assembly planning through a three-stage integrated

approach, International Journal of Production

Economics, 88, pp. 243-256.

Chen, S.-F., Liu, Y. (2001). The application of multi-level

genetic algorithms in assembly planning, Journal of

Industrial Technology, 17(4), pp. 1–9.

Chen, R.-S., Lu, K.-Y., and Yu, S.-C. (2002). A hybrid

genetic algorithm approach on multi-objective of

assembly planning problem, Engineering Applications

of Artificial Intelligence, 15, pp. 447–457.

Choi, C. K., Zha, X. F., NG, T. L. and Lau, W. S. (1998).

On the automatic generation of product assembly

sequences, International Journal of Production

Research, 36, pp. 617-633.

De Fazio, T. L., and Whitney, D. E. (1987). Simplified

generation of all mechanical assembly Sequences,

IEEE Journal of Robotics and Automation, Vol. RA-3,

No. 6, pp. 640-658.

De Lit, P., Latinne, P., Rekiek, B., and Delchambre, A.

(2001). Assembly planning with an ordering generic

algorithm, International Journal of Production

Research, 39(16), pp. 3623-3640.

Goldberg, D. E. (1989). Genetic algorithms in search,

optimization, and machine learning, Addison-Wesley,

Reading, MA.

Gottipolu, R. B., and Ghosh, K. (1997). Representation

and selection of assembly sequences in computer-

aided assembly process planning, International

Journal of Production Research, 35(12), pp. 3447-

3465.

Generation number

Cost

ICEIS 2008 - International Conference on Enterprise Information Systems

354

Heemskerk, D. J. M., and Van Luttervelt, C. A. (1989).

The use of heuristics in assembly sequence planning,

Annals of the CIRP, 38(1), pp. 37-40.

Homem de Mello, L. S., and Sanderson, A. C. (1991).

Two criteria for the selection of assembly plans:

maximizing the flexibility of sequencing the assembly

tasks and minimizing the assembly time through

parallel execution of assembly tasks, IEEE

Transactions on Robotics and Automation, 7(5), pp.

626-633.

Laperriere, L., and ElMaraghy, H. A. (1996). GAPP: A

Generative Assembly Process Planner, Journal of

Manufacturing Systems, 15(4), pp. 282-293.

Lazzerini, B., Marcelloni, F. (2000). A genetic algorithm

for generating optimal assembly plans, Artificial

Intelligence in Engineering, 14, pp. 319–329.

Li, J. R., Khoo, L. P., and Tor, S. B. (2003). A Tabu-

enhanced genetic algorithm approach for assembly

process planning, Journal of Intelligent

Manufacturing, 14(2), pp. 197-208.

Lin, A. C., and Chang, T. C. (1993). An integrated

approach to automated assembly planning for three-

dimensional mechanical products, International

Journal of Production Research, 31(5), pp. 1201-

1227.

Marian R. M. , Luong, L. H. S., and Abhary, K. (2003).

Assembly sequence planning and optimization using

genetic algorithms, Applied Soft Computing, 2/3F, pp.

223–253.

Santochi, M., and Dini, G. (1992). Computer-aided

planning of assembly operations: the selection of

assembly sequences, Robotics and Computer-

Integrated Manufacturing, 9(6), pp. 439-446.

Smith, S. S.-F. (2004). Using multiple genetic operators to

reduce premature convergence in genetic assembly

planning, Computers in Industry, 54, pp. 35–49.

Swaminathan, A., and Barber, K. S. (1996). An

Experience-based Assembly Sequence Planner for

Mechanical Assemblies, IEEE Transaction on

Robotics and Automation, 12(2), pp. 252-267.

Tseng, Y.-J., and Liou, L.-C. (2000). Integrating assembly

and machining planning using graph-based

representation models, International Journal of

Production Research, Vol. 38(12), pp. 2619-2641.

Tseng, Y-J, Lin, C-H, and Lin, Y-H. (2006). Integrated

assembly and machining planning for electronic

products using a genetic algorithm approach,

International Journal of Advanced Manufacturing

Technology, DOI 10.1007/s00170-006-0815-9,

Published online 17 November 2006.

Ye, N., and Urzi, D. A. (1996). Heuristic rules and

strategies of assembly planning: experiment and

implications in the design of assembly decision

support system, International Journal of Production

Research, 34(8), pp. 2211-2228.

A DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY PLANNING USING A GA

APPROACH

355