TOWARD A HYBRID ALGORITHM
FOR WORKFLOW GRAPH STRUCTURAL VERIFICATION
Fod´e Tour´e
1
, Karim Ba¨ına
1
and Walid Gaaloul
2
1
ENSIAS, Universit´e Mohammed V-Souissi, BP 713 Agdal, Rabat, Morocco
2
DERI-NUIG, IDA Business Park, Galway, Ireland
Keywords:
Business processes, business process validation, workflow structural checking, graph reduction, graph traver-
sal.
Abstract:
Appropriate definition, analysis, checking and improvement of business process models are indispensable
before their deployment within workflow management systems. In this paper, we focus on business process
model verification that insures business process structural correctness. Our proposal consist in a new hybrid
algorithm of workflow graph structural validation combining graph reduction and traversal mechanisms. Our
algorithm will be discussed and compared to existing workflow structural checking approaches.
1 INTRODUCTION
A process model is the formal definition of a busi-
ness process. The objective of a model is to produce
high-level specifications of workflows, independently
of workflow management system. Consequently, the
processes must be correctly modeled before they are
implemented as workflows.The invalid processes de-
ployment can lead processes-based applications to
states of incoherence and can even provoke very criti-
cal breakdowns without the slightest possibility of re-
sumption from where the interest of the validation of
the models of processes
There are several aspects in a process model includ-
ing the structure, the dataflow, the roles, the applica-
tion interface, the temporal constraints and others. In
a practical way and taking into account the life cycle
of a process (Sadiq et al., 2004), the process model
validation can be divided into three steps: structural
validation, contextual validation and pragmatic vali-
dation (Figure 1).
The structural validation (aka verification) consists
first in syntactic checking of the model by taking into
account the modeling language then in the basic mod-
els various combinations validation and possibly to
correct the model structure. The contextual validation
is not only interested in the internal structure of nodes
but also in their production influence on the neigh-
boring nodes behavior. The pragmatic validation is
interested in the checking of the re-usability of a valid
model in new run-time contexts.
Figure 1: Process life cycle and process of validation steps.
Process structure is the most important and pri-
mary aspect of a process model. It builds the base
to capture other aspects of the workflow needs. It is
why, in the suite of this paper, we will essentially be
interested in the structural validation.
Our paper is structured as follows: section 2 intro-
duces concept definitions, section 3 details our work-
flow verification algorithm, section 4 studies related
works, section 5 brings discussion elements, and sec-
tion 6 concludes.
2 CONCEPT DEFINITIONS
Workflow specifications use graphic objects. Most of
workflow management systems use a proprietary lan-
guage. However, Workflow Management Coalition
(W fMC) has developed a standard process definition
language and an interface specification which could
be used to transfer process models between products.
In this language, the processes are modeled by using
two object types: node and flow.
442
Touré F., Bäına K. and Gaaloul W. (2008).
TOWARD A HYBRID ALGORITHM FOR WORKFLOW GRAPH STRUCTURAL VERIFICATION.
In Proceedings of the Tenth International Conference on Enterprise Infor mation Systems - ISAS, pages 442-447
DOI: 10.5220/0001722404420447
Copyright
c
 SciTePress

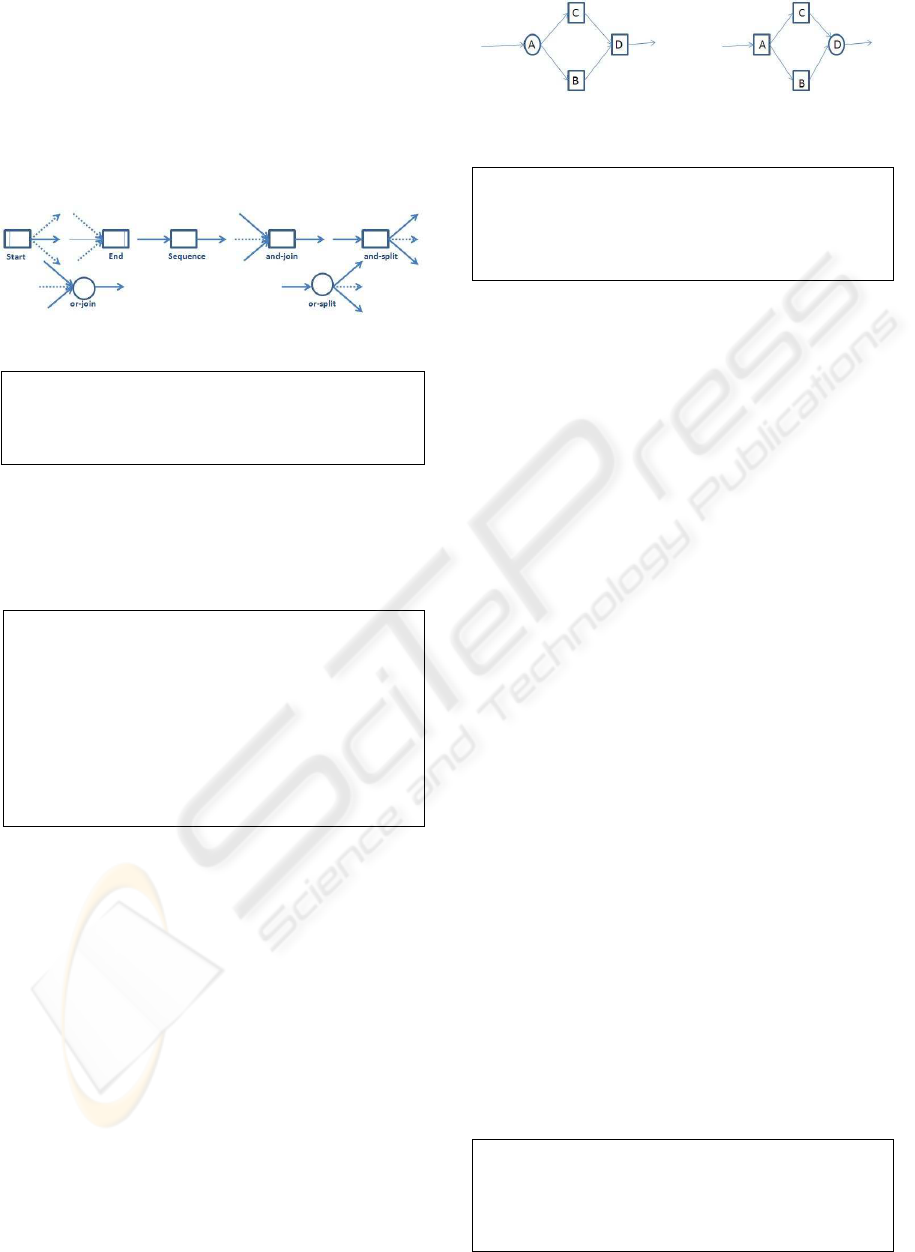
The node is classified in two categories: task and con-
dition. A task, graphically represented by a rectangle,
represents the work to be made to realize some ob-
jectives. A condition, graphically represented by a
circle, is used to build choice structures. A flow links
two nodes in graph and is graphically represented by
an arrow. Syntactically and in a basic way, objects
model have to verify following rules (Figure 2):
Figure 2: Process model objects syntactic rule.
Definition 2.1 (Structural validation). Structural validation
is all techniques used to identify objects incorrect combina-
tions, means allowing to avoid them or possibly to correct
them to increase the pre-execution reliability of a process.
A Directed Acyclic Graph (DAG) can contain two
types of structural conflict: deadlock (definition 2.2)
and lack of synchronization(definition 2.3)(Sadiq and
Orlowska, 1999; van der Aalst et al., 2002; Lin et al.,
2002)
Definition 2.2 (Process graph with deadlock). A process
graph contains a deadlock if it produces an instance sub-
graph which contains on the same path the following regu-
lar pattern (
or-split)t
∗
(and-join) where t is a task and t∗ a
path containing a sequence (eventually empty) of tasks.
Definition 2.3 (Process graph with lack of synchroniza-
tion). A process graph contains a lack of synchronization
if it produces an instance subgraph which contains on the
same path the following regular pattern (
and-split)t
∗
(or-
join) where t is a task.
As reduction goal is to delete valid structures to
verify graph correctness, the graph transformation by
introducing new objects or exchanging nodes order,
does not constitute a reduction rule because graph in-
tegrity is not respected.
The figure 7 is a graph which cannot be reduced by
the four first rules R
1
...R
4
of (Sadiq and Orlowska,
2000) thus, it is a split-join graph.
3 OUR WORKFLOW
VERIFICATION ALGORITHM
3.1 Algorithm Principle
Studying all publications around around structural
conflicts in workflow graph, we easily realize that in
Figure 3: Graph with dead-
lock.
Figure 4: Graph with lack
of synchronization.
Definition 2.4 (Workflow graph reduction). Workflow
graph reduction consists in deleting correct structures in
graph by respecting nodes Scheduling and making sure that
this deletion does not introduce new conflict or does not
delete existing conflict.
a process graph, any structural conflict is concerned
by a join node. Therefore, to detect a conflict in a
process graph, it is sufficient to localize split-join in-
correct combinations. However, this localization can
be very complex when we pass in the scale (graph is
too big), so it is important to reduce the size of the
graph according to the definition 2.4, while preserv-
ing nodes order.
Our approach consists in graph reducing at first then
in localizing incorrect combinations in graph by graph
traversal. For that purpose, we use seven rules
(R
1
...R
7
) of which four (R
1
...R
4
) of Sadiq-Orlowska
algorithm (Sadiq and Orlowska, 2000). As Sadiq-
Orlowska algorithm fifth rule applies to a split-join
graph particular case on four level and as the iden-
tification of the whole structure is very complicated,
we replaced it by the rules R
5
. . .R
7
which insure the
split-join graph correctness in a general way.
R
1
- Terminal Reduction Rule (Sadiq and Or-
lowska, 2000): the terminal reduction rule deletes
process graph beginning task and end task if the num-
ber of transitions attached to them is equal to one. The
beginning (respectively end) task deletion condition
implies that it is neither and-split nor or-split (is nei-
ther or-join nor and-join).
R
2
- Sequential Reduction Rule (Sadiq and Or-
lowska, 2000): If the current node forms a sequen-
tial structure, that means, if it has exactly one incom-
ing flow and one outgoing flow, the sequential rule
deletes the current node of the graph and deletes its
outgoing transition (the deleted node incoming tran-
sition will point to this last one outgoing node. G
Definition 2.5 (split-join graph). A split-join is graph that
contains only combinations of
split-join with split (respec-
tively
join) adjacent of different type. That kind of graphs is
irreducible by the four first rules of (Sadiq and Orlowska,
2000).
TOWARD A HYBRID ALGORITHM FOR WORKFLOW GRAPH STRUCTURAL VERIFICATION
443

Definition 2.6 (Correct join node). In a split-join graph,
a
join node which is not involved in a structural conflict is
correct.
Definition 2.7 (First level join Node). In a
split-join graph,
a first level
join node is a join node which has no other join
node as predecessor.
is a graph where f
1
(n
1
, n), f
2
(n, n
2
) ∈ F
2
⇒
R
2
G ::=
G
′
(N \ {n}, F ∪ { f(n
1
, n
2
)} \ { f
1
, f
2
})).
R
3
- Adjacent Reduction Rule (Sadiq and Or-
lowska, 2000): The adjacent reduction rule targets
two components types . If the current node is not
deleted neither according to the terminal reduction
rule nor the sequential reduction rule, it means that
it forms a structure (i) split or (ii) join.
(i) split structures fusion : If the current node
forms a split structure and has a single in-
coming transition and if the current node is
of the same type as its predecessors node, the
rule moves the current node outgoing tran-
sitions to the predecessors node and deletes
the current node (and-split associativity and
or-split associativity): ∀n
1
, n
2
, n
3
∈ N, (or-
split(or-split(n
1
, n
2
),n
3
)⇒
R
3
or-split(n
1
, n
2
, n
3
))
et (and-split(and-split(n
1
, n
2
),n
3
)⇒
R
3
and-
split(n
1
, n
2
, n
3
)) ;
(ii) join structures fusion : Otherwise if the cur-
rent node forms a join structure and has a
single outgoing transition and if the current
node is of the same type as its successors
node, the rule moves the current node incom-
ing transitions to the successors node and deletes
the current node (and-join associativity and or-
join associativity) : ∀n
1
, n
2
, n
3
∈ N, (or-join(or-
join(n
1
, n
2
),n
3
)⇒
R
3
or-join(n
1
, n
2
, n
3
)) et (and-
join(and-join(n
1
, n
2
),n
3
)⇒
R
3
and-join(n
1
, n
2
, n
3
));
R
4
- Closed Reduction Rule (Sadiq and Orlowska,
2000): Sequential and adjacent reduction rules ap-
plication introduce generally process graph deforma-
tions. Nodes of the same type can have more than one
transition between them (process graph becomes thus
not elementary). The closed reduction rule deletes all
transitions between such nodes except only one. G is
a graph where f
1
(n
1
, n
2
), f
2
(n
1
, n
2
) ∈ F
2
⇒
R
4
G ::=
G
′
(N, F \ { f
2
})
After application of previous rules, we obtain ei-
ther (1) an empty graph, or (2) a split-join graph. In
the first case, the original graph is without structural
conflict. In the second case (figure 7), next rules con-
sist in traversing the R
1
. . .R
4
resulting reduced pro-
cess graph seeking for not correct join nodes (as stated
in definition 2.6).
R
5
- Combination (split-join) Valid Rule:
1 For every join node, find the first split S
0
common
to all paths leading to the join node considered;
2 If current join node is of or-join type, to state that
the split-join combination is valid, it is necessary
to make sure that, according to S
0
outgoing transi-
tions activation, only one of the join node incom-
ing transitions is activated. Otherwise there is lack
of synchronization conflict.
3 If current join node is of and-join type, to state that
the split-join combination is valid, it is necessary
to make sure that, according to S
0
outgoing tran-
sitions activation, all incoming transitions of join
node are activated. Otherwise there is deadlock
conflict.
R
6
- Validation by Extension Rule: In a split-join
graph, the correctness of a join node, which has as pre-
decessors only correct join nodes, depends on the ac-
tivation of these last ones. Any and-join node, which
has as predecessors only correct join nodes, is cor-
rect if these nodes are simultaneously active. On the
other hand, any or-join node, which has as predeces-
sors only correct join nodes, is correct if it is always
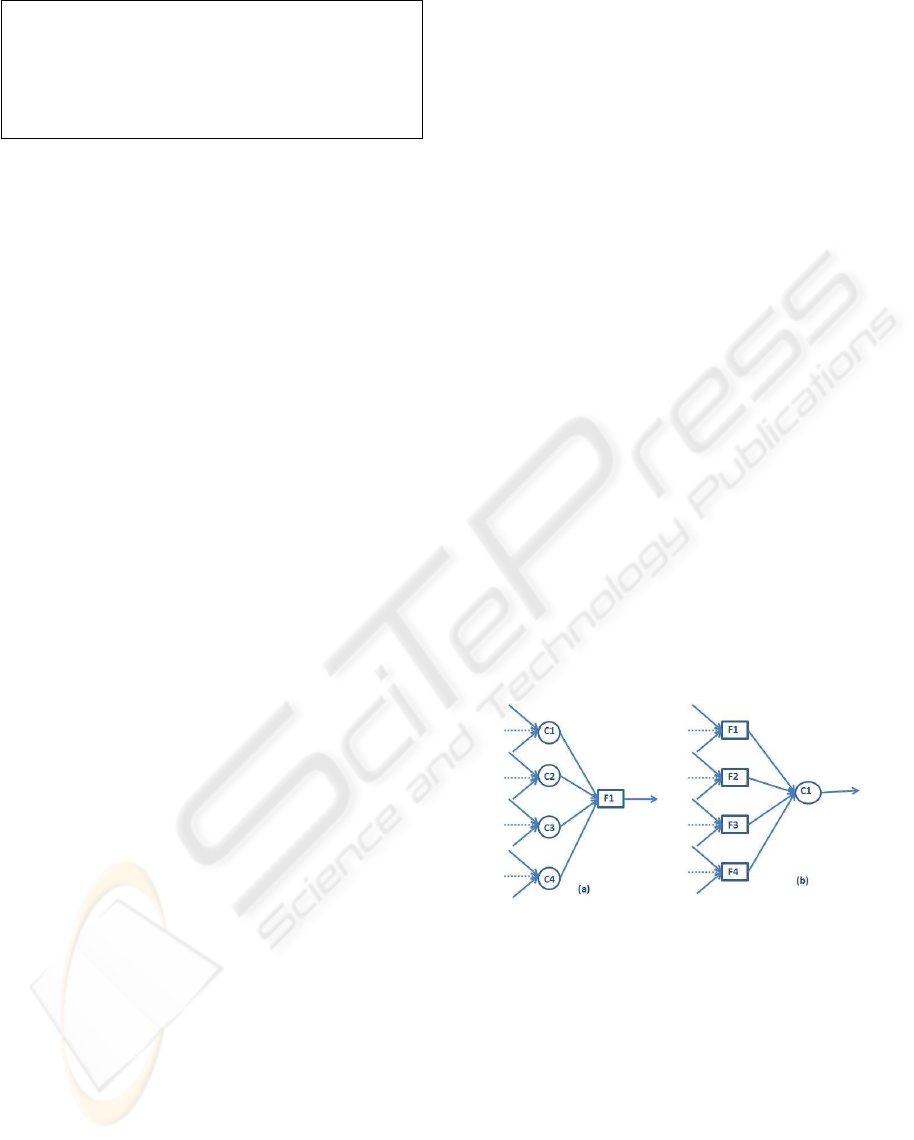
only one of these nodes that is active. In the figure 5
Figure 5: Validation by extension.
(a) F1 is correct if C1, C2, C3 and C4 are correct and
simultaneously active. On the other hand, in the fig-
ure 5 (b), if F1, F2, F3 and F4 are correct and active
simultaneously,C1 is not correct.
R
7
- Semi-validation by Extension Rule: In a
split-join graph, the correctness of a join node, which
has as predecessors correct join nodes and split nodes,
depends on the considered join node nature and the
activation or no of incoming flow from split nodes in
relation to the correct join nodes. In a model looking
like the figure 6 if the node B is correct, according
to the nature of the join node C, the correctness of C
ICEIS 2008 - International Conference on Enterprise Information Systems
444

Figure 6: Validation by semi-extension.
depends on the way of incoming transition activating
from the node A in relation to the node B. For the fig-
ure 6 particular case, node C is correct if nodes A and
B are not activated simultaneously. To verify the cor-
rectness in similar case, we are not obliged to make a
graph traversal, we use only the relation enter A, the
split S
0
of B and join node C nature.
3.2 Our Algorithm
Require: G respecting the preconditions (hypotheses)
Ensure: Reduce(G) =true iff G is valid ; false else
G
′
←− G
lastsize ←− size[G
′
] + 1
while (lastsize > size[G
′
]) do
lastsize ←− size[G
′
]
Pass 1 : apply to G
′
terminal reduction rule (R
1
), then
sequential reduction rule (R
2
), then adjacent reduction
rule (R
3
).
if (lastsize < size[G
′
]) then
Pass 2 : apply to G
′
closed reduction rule (R
4
).
end if
end while
if (graph G
′
is empty) then
% the original graph G is valid
return true 
else
% the original graph G
′
is a split-join graph
G” ←− G
′
% rules R
5
, R
6
, R
7
application
Seek all join nodes N j of the graph G”
for all N j do
if first level(N j) then
Pass 3 : apply to G” the rule(R
5
).
Find the first Split S
0
common to all paths lead-
ing to the considered join node N j;
According to the activation of S
0
outgoing flows;
if correct(N j) then
% correct split-join combination
else
% The graph G contains a structural conflict
return false 
end if
else
apply to G” the rule(R
6
).
if correct(N j) then
% correct split-join combination
else
% The graph G contains a structural conflict
return false 
end if
else
apply to G” the rule(R
7
).
if correct(N j) then
% correct split-join combination
else
% The graph G contains a structural conflict
return false 
end if
else
Find the first Split S
0
common to all paths lead-
ing to the considered join node N j;
According to the activation of S
0
outgoing flows;
if correct(N j) then
% correct split-join combination
else
% The graph G contains a structural conflict
return false 
end if
end if
end for
% the original graph G is valid
return true 
end if
3.3 Application Example
In this section, we are going to apply our algorithm
to a process model. For that purpose, we choose a
model proposed by (Lin et al., 2002) as counter ex-
ample to prove that the Sadiq-Orlowska algorithm is
not complete.
Figure 7: split-join graph (Lin et al., 2002).
The figure 7 (Lin et al., 2002) shows an irreducible
model by the four first rules of Sadiq-Orlowska algo-
rithm (Sadiq and Orlowska, 2000) thus, it is a split-
join graph. Our algorithm rules R
5
, R
6
, R
7
application
on this model is presented in the table 1 below.
Our algorithm application on the figure 7 model
shows that this last one is without structural conflict
because all join nodes are correct (definition 2.6). It is
important to note that in our algorithm, the rule (R
5
)
is effectively applied only for first level join nodes.
Thus, for a higher level join node, the verification is
insured by rules R
6
, R
7
. In other words, we make the
(split-join) graph partial traversal only to verify the
correctnessof first level join nodes. For the remainder,
we study lower level join nodes behavior.
TOWARD A HYBRID ALGORITHM FOR WORKFLOW GRAPH STRUCTURAL VERIFICATION
445

Table 1: Our algorithm application on figure7 graph.
Join
Node
Split
S
0
Traversal Stat Obs
M1
(or)
C1
(or)
C1→F1→C2→F4→M1
C1→F2→M1
one active flow on
two
correct
R
5
M2
(or)
C1
(or)
C1→F1→C2→F4→M2
C1→F2→C3→F5→M2
C1→F2→C3→F6→M2
one active flow on
three
correct
R
5
M3
(or)
C1
(or)
C1→F1→C2→F3→M3
C1→F1→C2→F4→M3
C1→F2→C3→F5→M3
one active flow on
three
correct
R
5
M4
(or)
C1
(or)
C1→F1→M4
C1→F2→C3→F5→M4
one active flow on
two
correct
R
5
S1
(and)
correct(M1)=true ; cor-
rect(M2)=true
Two active flows on
two
correct
R
6
S2
(and)
correct(M3)=true ; cor-
rect(M4)=true
Two active flows on
two
correct
R
6
M5
(or)
C1
(or)
correct(S1)=true
C1→F1→C2→F3→M5
one active flow on
two
correct
R
7
M6
(or)
C1
(or)
correct(S2)=true
C1→F2→C3→F6→M6
one active flow on
two
correct
R
7
S3
(and)
correct(M5)=true ; cor-
rect(M6)=true
Two active flows on
two
correct
R
6
4 STATE OF THE ART
As we exposed it in section 2, a process graph con-
tains two structural conflict: deadlock and lack of
synchronization (Sadiq and Orlowska, 2000). In the
goal to verify or to assure the correctness of a process
model, several propositions were made among oth-
ers: reduction-basedalgorithms (Sadiq and Orlowska,
2000; Lin et al., 2002), graph-traversal-based algo-
rithm (Perumal and Mahanti, 2005; Perumal and Ma-
hanti, 2007), approach of transformation of not valid
model in valid model (Liu and Kumar, 2005) and ap-
proach of model conversion in Petri net (van der Aalst
et al., 2002). As our approach does not concern this
last point, we are not going to present it in this paper.
Sadiq-Orlowska Algorithm. This algorithm con-
sists in deleting of all certainly correct structures in
a workflow graph. The process of reduction reduces
finally a structurally correct workflow graph in an
empty graph. On the other hand, a workflow graph
with structural conflict is not completely reduced.
The process of reduction uses five reduction rules
- terminal, sequential, adjacent, closed and over-
lapped - as long as they are capable to reduce the
graph. These reduction rules are applied by visiting
all graph nodes and verifying if a reduction rule can
be applied.
The complexity of the algorithm worst cases is
O((size(G))
2
) where size(G) = |N| + |F| (Sadiq and
Orlowska, 1999).
Lin-Zhao-Li-Chen Algorithm. By using figure 7
model, Lin-Zhao-Li-Chen demonstrated that Sadiq-
Orlowska algorithm is limited because he cannot re-
duce, in empty graph, models which are neverthe-
less correct (what we called split-join graph). So,
Lin-Zhao-Li-Chen algorithm is an improvement of
Sadiq-Orlowska. This algorithm is based on seven
reduction rules of which the four first of Sadiq-
Orlowska algorithm: terminal, sequential, adja-
cent, closed, choice-convergence, synchronizer-
convergence, merge-fork (Lin et al., 2002). Its theo-
retical complexity is O(|N| + |F|)
2
.|N|
2
) where |N| is
the number of nodes and |F| is the number of transi-
tions (flow).
Mahanti-Sinnakkrishnan Algorithm. This algo-
rithm uses properties and methods of the algorithms
”Traversal in depth” (Depth-First Search: DFS) and
AO∗ to create and verify a workflow graph various
instance subgraphs. The properties of the algorithm
AO∗ are used to choose only select instance subgraphs
in a way that verifying this subset of instance sub-
graphs is equivalent to the verification of the com-
plete workflow graph. In this algorithm, the structural
conflicts are identified after two Traversals in depth
of every instance subgraph by using the operations:
Create-Instance-Subgraph(CIS) and Verify-Instance-
Subgraph (VIS). Its complexity, according to them, is
O(|F|
2
) where |F| is the number of transitions (flow)
(Perumal and Mahanti, 2005).
5 DISCUSSION
Our algorithm interest compared to the reduction ex-
plains itself by the fact that it is complete and sim-
pler. It verifies any acyclic workflow graph without
transformingit. Compared to our algorithm, Mahanti-
Sinnakkrishnan algorithm is less efficient because it
makes useless traversals. In our approach, the reduc-
tion is applied when it is necessary ”to simplify” the
graph and the search is applied in a partial and lo-
calized way. Thus, the hybridization gathers the best
both graph traversal and reduction. In the aim of as-
suring a good understanding of the of this paper, it is
necessary to define certain properties.
Property 5.1 (Termination). an algorithm terminates if
it doesn’t lead to an abnormal break during its execution.
Property 5.2 (Correctness). a correct algorithm must
answer, after termination, by the affirmative or the negative
according to the result of the execution.
Property 5.3 (Completeness). an algorithm is complete
if it verifies the structural correctness of any graph.
Property 5.4 (Transformation). an algorithm trans-
forms a graph if, during verification, it changes nodes order
or introduces new node into the graph.
ICEIS 2008 - International Conference on Enterprise Information Systems
446

Table 2: Workflow verification algorithms Comparison.
Completeness Transformation Complexity
Sadiq-Orlowska No No O((|N| + |F|)
2
)
Lin-Zhao-Li-Chen Yes Yes O((|N| + |F|)
2
.|N|
2
)
Mahanti-Sinnakkrishnan Yes No O(|F|
2
)
Tour
´
e-Ba
¨
ına Yes No O(|K|
2
+ |F
′
|
2
)
Taking into account properties above and what is
exposed higher in this paper, we can affirm that (1) for
termination, our algorithm finishes by convergence
of the reduction and the traversal; (2) for correctness,
our algorithm answers YES when it is correct and NO
otherwise; (3) for completeness, our algorithm ver-
ifies the correctness of any graph, same complexes;
and (4) for transformation, our algorithm does not
transform the graph because it does not change nodes
order and does not introduce new node. Our algo-
rithm begins with the application of the four first rules
R
1
...R
4
reduce graph size. This choice takes into ac-
count the fact that if the workflow graph G
i
is the
graph obtained after application of i iterations of the
rules R
1
to R
4
on G, then: reduction rules do not pro-
duce structural conflicts, that means, if G
i
is correct
then G
i+1
is correct; reduction rules do not delete
structural conflicts, that means, if G
i
is incorrect then
G
i+1
is incorrect; and, If the application of rules R
1
to R
4
cannot reduce G to an empty graph then G
i
has
to be a graph split-join otherwise G will always be re-
duced to an empty graph. In case where graph is not
completely reducible, the rule R
5
allows to verify the
correctness of first level join nodes by making a partial
and localized traversal of the graph. For others join
nodes, we apply rules R
6
, R
7
or a simple deduction by
using predecessors correct join nodes behavior.
Algorithm complexity is O((|N| + |F|)
2
) where |N| +
|F| represents the number of nodes and transition in
the workflow graph (Sadiq and Orlowska, 2000), in
case the graph is completely reducible by rules R
1
to
R
4
. The average case complexity is much lower in
O((|N| + |F|)
2
), since the first iterations reduce radi-
cally workflow graph size.
In case where the graph is not reducible (split-join
graph), the worse case is that R
5
is the only applica-
ble rule to verify join nodes correctness. In that case,
we would be obliged to traverse the entire new graph.
But, as this case does not exist in a split-join graph
then our algorithm complexity is theoretically lower
than that of the graph traversal in depth algorithm.
Thus more efficient with a complexity O(|F
′
|
2
) where
|F
′
| is the number of transition between join first level
nodes and their split S
0
. In the final, in the worst
of the cases, reduction O(|K|
2
) + traversal O(|F
′
|
2
)
gives an algorithm in O(|K|
2
+ |F
′
|
2
) where |K| is the
number of reducible node and transition and |F
′
| is
the number of transition between first level join nodes
and their split S
0
. Table 2 compares verification algo-
rithms according to defined properties.
6 CONCLUSIONS
Through this paper you discovered a new effective
and complete algorithm that verifies the structural
correctness of any acyclic workflow graph by hy-
bridizing the graph reduction and traversal. In our
perspective, we work on our algorithm application for
cyclic workflow graphs structural verification through
a workflow graph structural verification tool.
REFERENCES
Lin, H., Zhao, Z., Li, H., and Chen, Z. (2002). A novel
graph reduction algorithm to identify structural con-
flicts. In HICSS, page 289.
Liu, R. and Kumar, A. (2005). An analysis and taxonomy
of unstructured workflows. In Business Process Man-
agement, pages 268–284.
Perumal, S. and Mahanti, A. (2005). A graph-search based
algorithm for verifying workflow graphs. In DEXA
Workshops, pages 992–996. IEEE Computer Society.
Perumal, S. and Mahanti, A. (2007). Applying graph search
techniques for workflow verification. In HICSS,
page 48.
Sadiq, S., Orlowska, M., Sadiq, W., and Foulger, C.
(2004). Data flow and validation in workflow mod-
elling. In ADC ’04: Proceedings of the 15th Aus-
tralasian database conference, pages 207–214, Dar-
linghurst, Australia, Australia. Australian Computer
Society, Inc.
Sadiq, W. and Orlowska, M. E. (1999). Applying graph re-
duction techniques for identifying structural conflicts
in process models. In CAiSE, pages 195–209.
Sadiq, W. and Orlowska, M. E. (2000). Analyzing process
models using graph reduction techniques. Inf. Syst.,
25(2):117–134.
van der Aalst, W. M. P., Hirnschall, A., and Verbeek, H. M.
W. E. (2002). An alternative way to analyze workflow
graphs. In CAiSE, pages 535–552.
TOWARD A HYBRID ALGORITHM FOR WORKFLOW GRAPH STRUCTURAL VERIFICATION
447