
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE
SEARCHING
Exemplieied by CT Data of Patient
Jyhjeng Deng
Industrial Engineering & Technology Management Department, DaYeh University
112 Shan-Jeau Rd., Da-Tsuen, Chang-Hua, Taiwan
Keywords: Correspondence Analysis, Fisher’s linear Discriminant function, multivariate categorical data, parallel
coordinate plots.
Abstract: In the process of searching classification rules for multivariate categorical data, it is crucial to find a quick
start to locate the combination of levels of input and response variables which can contribute to the most
correct classification rate for the response variable. Fisher’s linear discriminant function is proposed to
select some important input-variable candidates; then, correspondence analysis is used to ascertain that the
level of candidates is closely related to the appropriate level of response variable. The closest linkage
between input variable and response variables is chosen as the rule for each input-variable candidate. The
algorithm is applied to the hospital data of patients whose CT scan diagnosis awaits a decision. The result
shows that my algorithm is not only quicker than an exhaustive search but the result is also identical to the
optimum solution by exhaustive search in terms of the correct classification rate. The correct classification
rate is about 80%. Finally, two parallel coordinate plots of the 20% mistakenly classified data and the
corresponding correctly classified data are compared, showing their mutual confounding and explaining
why the correct classification rate cannot be further improved.
1 INTRODUCTION
Patients sent to the emergency unit of a hospital
need immediate care to save their life. To attend to
patients in an appropriate manner, correct treatment
is crucial, leading to the issue of making a correct
diagnosis. In this investigation a data set on 959
patients sent to a local hospital within a certain
period of time for emergency care is collected. The
on duty physicians face the decision whether the
patients need head-computed tomography (HCT),
more commonly known as computed axial
tomography (CAT or CT scan). Since each patient
differs, a rule based on the physical characteristics
(such as blood pressure, breath, mental status, and
triage level, etc.) of the patient should be formulated
to help the physician make an appropriate decision
on the need for HCT. The first 80% (767) of the
original data is used as a training set to establish the
rule; whereas, the second 20% (192) is used as test
data to demonstrate the effectiveness of the rule.
The data set contains seven independent
variables, A1-A7 (such as sex, age, triage level,
mental status, breathing rate, diastolic blood
pressure and pulse rate) and one response variable,
HCT (D). The medical data are further classified by
the physician as in the contingency table shown in
Table 1 in Appendix A. Note that D has two
meanings: (1) the response variable of the HCT,
being the highest standard determined by the on-
duty physician, and (2) the result determined by the
classification rule. At first the double meaning might
be somewhat confusing, but it eliminates the need to
define another variable, as should be clear from the
context as this report proceeds.
A simple and direct way to solve the problem is
enumeration, an exhaustive method. In the single-
variable rule search, there will be
2
p
ways to
classifiy a categorical input variable with p levels
into a response variable of 2 levels . For example, to
find the best rule for variable A3 (with three levels)
which will provide the most correct classification via
HCT (with two levels), the correct rate for the
following six rules must be computed: (A3=1, D=1),
(A3=1, D=2), (A3=2, D=1), (A3=2, D=2), (A3=3,
D=1), (A3=3, D=2). Since there are seven
278
Deng J. (2008).
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE SEARCHING - Exemplieied by CT Data of Patient.
In Proceedings of the Tenth International Conference on Enterprise Information Systems, pages 278-286
DOI: 10.5220/0001723702780286
Copyright
c
SciTePress

independent variables and each is classified as 2, 5,
3, 4, 3, 3 and 4 levels, 2*(2+5+3+4+3+3+4)=48
rules need to be evaulated. The classification rule
(A3=1, D=1) means that if the patient’s triage level
is 1, he/she needs to have the HCT. This decision is
applied to the training data; however, it may be
incorrect according to the criterion of response
variable D. Thus, a correct rate can be calculated,
and the highest correct rate chosen. In this case,
when dealing with only one independent variable,
the obtained rule is applied to the test data set to
determine whether this rule can render a similar
correct classification rate. This type of selection
procedure can be applied to the two independent
variables. When variable
1
x has
1
l levels and
variable
2
x has
2
l levels, then there are 2
12
ll
rules to be evaluated. In this case study, there will be
2*(2*5+2*3+2*4+2*3+2*3+2*4+5*3+5*4
+5*3+5*3+5*4+4*3+4*3+4*4+3*3+3*4+3*4)= 404
rules altogether. Clearly, evaluating each in
succession is very time consuming; therefore, a
faster, more reliable method should be sought. For
this purpose, two multivariate techniques are used to
solve the problem in sequence. First, Fisher’s linear
discriminant function is built and important input
variables selected. By following the correspondence
analysis, the level from the input variable closest to
the level of the response variable can be selected as
the classification rule. For example, variable triage
(A3) is considered to be one of the most important
of the seven independent variables. Then, a
Euclidean distance can be derived between the level
of independent variable A3 and the level of decision
variable D. The shortest distance between them is
chosen as the classification rule for input variable
A3. By extending the aforementioned procedure for
a single variable to two variables, a combination of
composite rules to determine the optimum correct
classification rate can be established, in this case
about 80%. Finally, two parallel coordinate plots of
the 20% mistakenly classified data and the
corresponding correctly classified data are compared,
showing their mutual confounding and explaining
why the correct classification rate cannot be further
improved. Although Fisher’s linear discriminant
function and correspondence analysis are two well
known techniques in multivariate analysis, using
them together to find the classification rule for
multivariate categorical data is unusual. Fisher’s
function is mostly used to classify multivariate
continuous data into various categories. In the
literature, one can find its application to face
detection (
Yang, Kriegman and Ahuja, 2001) and its
combination with linear programming (
Lam and Moy,
2003). Used to detect the root of two categorical
variables. Correspondence analysis can be used in
the ecological study of animal populations (
Allombert,
Gaston and Martin, 2005
).
2 FISHER’S LINEAR
DISCRIMINAT FUNCTION
Suppose that there is a sample data set X of
multivariate variable
x composed of samples
j
X
with sample size of
j
n , 1, 2, ,j J= L , from
J
populations. To obtain the optimum classification
rule for multivariate sample
X , Fisher suggests
finding the linear combination of
T
ax which
maximizes the ratio of between-group-sum of
squares to the within-group-sum of squares (Hardle
and Simar, 2003),
T
T
aBa
aWa
, (1)
where
B is the between-group-sum of squares,
defined as (Johnson and Wichern, 2003)
()()
1
J
T
ii i
i
B nx x x x
=
=−−
∑
; (2)
whereas,
W is the within-group-sum of squares,
defined as
()()
11
i
n
J
T
ijiiji
ij
Wxxxx
==
=−−
∑∑
. (3)
Note that
ij
x represents the
th
j sample from
population
i ;
i
x , the sample mean of population i ;
x
, the grand average of the total samples. The
solution of vector
a is found in Theorem 1 (Hardle
and Simar, 2003).
Theorem 1. The vector
a that maximizes (1) is the
eigenvector of
1
WB
−
corresponding to the largest
eigenvalue.
Now, the pertinent discrimination rule is as follows:
Classify
x into group j where
T
j
ax is closest to
T
ax. When J =2 is grouped, the discriminant rule
is computed as follows: The corresponding
eigenvector in Theorem 1 is
1
12
()aW x x
−
=−.
The corresponding discriminant rule is
M
279
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE SEARCHING - Exemplieied by CT Data of Patient

()
()
1
2
if 0
if 0
T
T
xaxx
xaxx
→Π − >
→Π − ≤
, (4)
where
i
Π represents population i .
Note that all the data are not assumed to be normal;
the only assumption is that they are real numbers.
After this short introduction to Fisher’s linear
discriminant function, the focus is now directed
toward its application to the hospital data. To sketch
the eight variables of 767 data set, parallel
coordinate plots are used. The result is shown in
Appendix B. Since variable A1 is nominal and the
analysis in Appendix B indicates that variable A1
has no strong correlation with variable D. Fisher’s
linear discriminant function with input variables
(A2-A7) is found. Vector
a is [0.00023445, -
0.00079367, 0.00062467, 0.0020182, -2.9766e-06, -
0.00035162]
T
; the grand average
x
is [3.4433,
1.7901, 1.1917, 1.9974, 2.9126, 2.3051], the values
in
a and
x
corresponding to variables A2-A7.
Then, the number of individuals coming from
j
Π
,
which have been classified into
i
Π by
ij
n , are
denoted. By applying the discriminant rule in Eq. (1)
to the test data set, one has
12
n =0 and
21
n =48, the
correct classification rate being 0.75. By examining
the magnitude of the coefficients in
a , it is clear
that the three most important variables are A5
(breathing), A3 (triage) and A4 (mental state);
whereas, the least important is A6 (blood pressure).
Thus, the correlation between the level of these
variables and the CT level is investigated and the
closest relationship between them in terms of the
Euclidean distance searched. The closest is chosen
as the rule to classify the patients who need HCT. A
detailed explanation follows.
3 CORRESPONDENCE
ANALYSIS
The aim of correspondence analysis is to develop
simple indices showing relationships between the
rows and columns of a contingency table, wherein
row and column represents one category of the
corresponding variables. The entry
ij
x
in table
Χ
(with dimension (nxp)) represents the number of
observations in a sample which simultaneously fall
in the i
th
row category and the j
th
column category,
for
1, 2, ,in= L and 1, 2, ,
j
p
=
L . Then the
association between the row and column categories
can be measured by an
2
χ
-test statistic defined as
()
2
2
11
/ ,
p
n
ij ij ij
ij
x
EE
χ
==
=−
∑∑
(5)
where
..
..
ij
ij
x
x
E
x
= with
.i
x
represents the sum in
the i
th
row;
.
j
x
, the sum in the j
th
column; and
.. .
1
n
i
i
x
x
=
=
∑
, the grand total. Under the hypothesis of
independence,
2
χ
has an
2
(1)( 1)np
χ
−−
distribution. If
the test statistic
2
χ
is significant at the 5% level,
investigating the special reasons for the departure
from independence is worthwhile. To extract the
elements of dependence, the principle of
correspondence analysis (CorrAna) is brought into
play. The CorrAna procedure first determines the
SVD (singular value decomposition) of matrix
C
(nxp) with elements (Hardle and Simar, 2003)
(
)
1/2
/
ij ij ij ij
cxEE=− . (6)
When assuming that the rank of
C is
R
, the SVD
of
C yields
T
C
=
ΓΛΔ , (7)
where
Γ
contains the eigenvectors
k
γ
(nx1) of
T
CC ,
Δ
the eigenvectors
k
δ
(px1) of
T
CC
where
k
=
1,2,…,R and
()
1/2 1/ 2
1
diag , ,
R
λλ
Λ= L
(where diag represents the diagonal matrix) with
12 R
λ
λλ
≥≥≥L (the eigenvalues of
T
CC ). By
defining the matrices
A (nxn) and
B
(pxp) as
(
)
()
..
diag and diag
ij
A
xB x==, (8)
one can calculate
k
r (nx1) and
k
s (px1),
1, 2, ,kR
=
L as
1/ 2
1/ 2
,
,
kk k
kk k
rA
sB
λ
γ
λ
δ
−
−
=
=
(9)
where point vectors [
1
r ,
2
r ] and [
1
s ,
2
s ] are
plotted onto a two-dimensional graph, called biplot,
with n points in point vector [
1
r ,
2
r ] representing
the n rows and p points in [
1
s ,
2
s ] representing the
p columns. Thus, the entire contingency table can be
simplified as n+p points on the 2D graph. The
ICEIS 2008 - International Conference on Enterprise Information Systems
280
relationship between n points [
1
r ,
2
r ] and p points
[
1
s ,
2
s ] explains why rows and columns are not
independent.
Now, the correspondence analysis (CorrAna) is
applied to the contingency table of variables A5 and
D as an illustration, shown in Table 1.
Table 1: Contingency table of variables A5 and D for 767
Data.
HCT (D)
1 2
Breath
(A5)
<10/min 1 4
10~24/min 249 510
>24/min 3 0
The corresponding
R of
C
for Table 1 is 1;
moreover, vector
1
r =[-0.2762, -0.0038143, 1.4253]
and vector
1
s =[0.13109, -0.064523]. Since R =1,
there are no
2
r and
2
s . A zero vector is substituted
for
2
r and
2
s to make a 2D biplot, shown in Fig. 1.
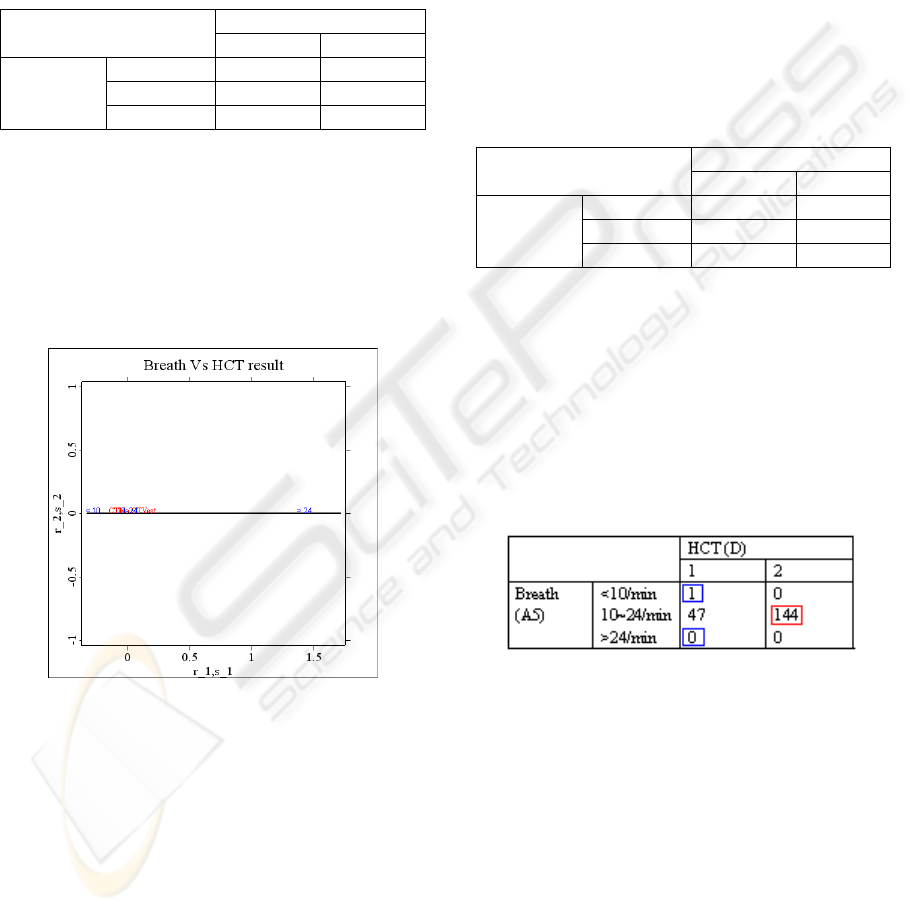
Figure 1: Biplot of variables A5 and D.
Note that the two levels of response variable D
(CTYes corresponding to HCT [D=1] and CTNo,
HCT [D=2]), are close to the second level of
independent variable A5. Examining the value of
1
r
(representing A5) and
1
s (representing D), one may
clearly observe that HCT (D=2) is closer to (A5=2)
than HCT (D=1). The value of HCT (D=2) in Figure
1 is -0.064523, being the second value in
1
s ; the
value of (A5=2), -0.0038143, being the second value
in
1
r ; the value of HCT (D=1), 0.13109, being the
first value in
1
s . The rule is then derived as if
(A5=2); therefore, HCT should not be administered.
Thus when the breathing level is normal, the patient
does not need HCT. By applying this rule to the
remaining test data, one has
12
n =0 and
21
n =47, the
correct rate being 0.75521. Table 1 clearly indicates
that the rule is optimum; hence, any other rule will
yield a worse correct rate. The effectiveness of
applying this rule to the test data can be clearly
observed by scrutinizing the contingency table of
variables A5 and D for the test data set, shown in
Table 2.
Table 2: Contingency table of variables A5 and D for 192
Data.
HCT (D)
1 2
Breath
(A5)
<10/min 1 0
10~24/min 47 144
>24/min 0 0
The rule can be applied to Table 2 to obtain Figure 2,
where the correct result from the main rule (if
[A5=2] then do not administer HCT) is marked in
red; whereas, the correct result from the congruent
rule (if [A5≠ 2] then administer HCT) is marked
in blue. The correct rate is (1+0+144)/192=0.75521.
No other classification rule will result in a better
correct rate.
Figure 2: Classification rule with contingency table.
By applying the same procedure to the contingency
tables of variables A3 and D, and A4 and D, the
correct rates of 0.70312 and 0.72396, respectively,
are obtained. The rules derived are if (A3=1), then
HCT (D=1); and if (A4=2), then HCT (D=1),
respectively. These values indicate that when the
triage level is 1, the patient needs HCT; and when
the mental status is ‘to call’, HCT, respectively. The
corresponding biplots are shown in Figures 3 and 4.
For the sake of analytical completeness, the
contingency tables of variables A1-A7 vs D for both
the training and the test data sets are listed in
Appendix C.
M
281
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE SEARCHING - Exemplieied by CT Data of Patient

Figure 3: Biplot of variables A3 and D.
Figure 4: Biplot of variables A4 and D.
From the data reported in Appendix C and previous
results, one may assert that analysis by Fisher’s
linear discriminant function and CorrAna provides a
quick start for identifying the important input
variables for searching the classification rule. In this
case the important input variables are A3, A4 and
A5, being in agreement with the Chi-squares test on
the contingency table shown in Appendix C.
Furthermore, the rule provided by CorrAna is in
very strong agreement with the exhaustive search,
with only a small difference in the rule for A4. The
rules by CorrAna for each important variable are: if
A3=1 then D=1; if A4=2, then D=1; if A5=2 then
D=2. These rules differ from the ones obtained by
exhaustive search only in variable A4, where if
A4=1 then D=2; however, there is no difference in
the correct classification rate.
The optimum correct classification rate by the
single-variable classification rule is 0.75521,
provided by the rule of input variable A5, where if
(A5=2) then D=2. Further research is needed to find
composite classification rules for two variables
which, perhaps, would render a higher correct rate.
The result of two-variable classification is explained
below and listed in the combination of composite
rules.
4 OPTIMUM RULE OF
COMBINATION FOR TWO
VARIABLES
Following the previous arguments, the combination
rule for two variables is straightforward. For the
sake of simplicity, only the procedure for finding the
optimum correct rate is illustrated. Variables A3 and
A4 are used to form a new variable, A9, where
A9=(A3-1)*4+A4. (10)
Here A9, A3 and A4, in addition to designating
the composite variable name, triage and mental
status, also represent the level of the corresponding
variables. Since the level of variable A3 is three and
that of A4 is 4, the level of A9 indicates the
combination level of A3 and A4, as shown in
equation (10). For example, when A9=9 the equation
denotes that A3=3 and A4=1. Theoretically, the total
level of A9 is 12; however, in this case study it is
only 10 because levels 11 and 12 of A9 are missing.
Therefore, the frequencies of (A3=3 and A4=3) and
(A3=3 and A4=4) are zero with regard to both levels
of HCT response variable (D). Applying CorrAna to
A9 with regard to response D, the biplot shown in
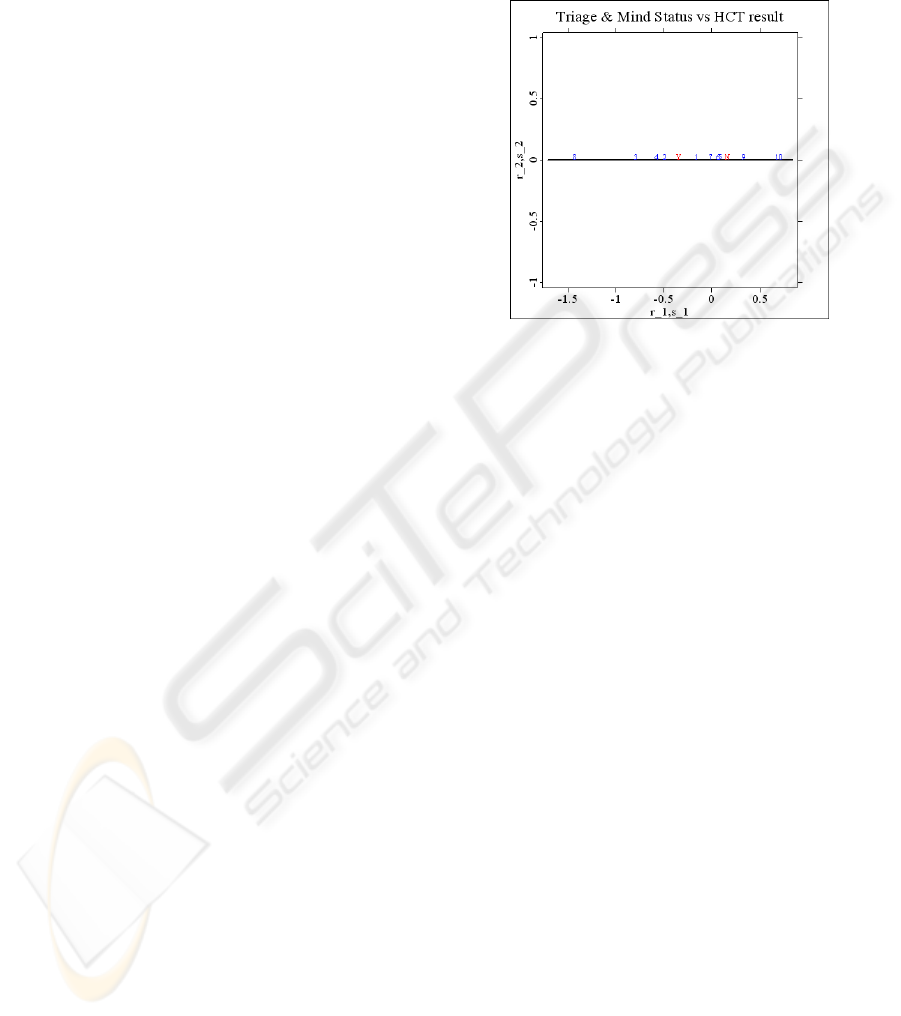
Figure 5 is obtained.
For a clearer display, the labels of the levels of
response D are changed from ‘CTYes’ and ‘CTNo’
to ‘Y’ and ‘N’. It is clear from Figure 5 that levels 8,
3, 4 and 2 are located to the left of ‘Y’ and levels 10
and 9 to the right of ‘N’; whereas, the other levels
remain between ‘Y’ and ‘N.’ Thus, it can be said
that when (A3=2 and A4=4) or (A3=1 and A4=3 or
4 or 2), then one should judge D=1; whereas, when
(A3=3 and A4=2) or (A3=3 and A4=1), then D=2.
Therefore, when the triage level is 2 and the mental
status level is a coma, or when the triage level is 1
and the mental status is unclear, one should judge
HCT to be necessary. In such cases, the patients are
in serious conditions; thus, administering HCT is
appropriate and useful in diagnosing the root
problem. However, when patient is in a level 3 triage
and the mental status is clear or one capable of
responding to a verbal stimulus, HCT is unnecessary.
Note that in these two cases, the patients are in better
condition, but that many patients do not fall into
either of these stated categories. To overcome this
ICEIS 2008 - International Conference on Enterprise Information Systems
282
problem, the single rule of ( if A5=2, D=2 )is
applied to the remainder.
It is worth noting that the single variable rule, the
shortest Euclidean distance between the levels of the
independent and the response variables is chosen as
the classification rule; whereas, in the two-variable
rule, the levels of the composite formed by the two
variables on each side of the response variable is
chosen as the composite rule. These principles are
true because in the single-variable case, once the
main classification rule has been set, its complement
(congruent) is automatically determined. For
example, in the case of A5 and D, as shown in
Figure 2, once the main rule, if (A5=2) then D=2, is
set, its complement, if (A5 ≠ 2) then D=1, is
automatically determined. Note that (A5≠ 2) means
that (A5=1 or 3). Therefore, once the destiny of
(A5=2) is determined as D=2, the other choices of
A5 have a pre-determined result. Thus, a reasonable
choice for the classification rule can be based on the
shortest linkage between the levels from the
independent and the response variables.
If the same argument is followed in the two-
variable case, then there is only one level in the
composite variable A9 which can be associated with
one of the two levels of D. The other values of A9
will be assigned with the alternative value of D, a
procedure which does not make good sense since the
other values are not necessarily exclusive with the
chosen value in the main rule. To clarify this point,
an illustrative example is given as follows. If the
shortest distance between level 5 of A9 and level 2
of D is chosen as the classification rule, then by the
same argument in single-variable, level 5 of A9
should be associated with level 2 of D and other
values (these include level 9, of course) of A9
should be with level 1 of D. However, Figure 5
clearly shows that level 9 of A9 should be associated
with level 2 of D since it is closely associated with
level 2 of D by the interpretation of correspondence
analysis (Hardle and Simar, 2003). Thus, the only
reasonable classification rule is to divide the levels
of the composite variable into three regions with the
levels of D as the demarcation points. With the
levels in the middle region undecided, the levels in
the left region are associated with the left
demarcation point; whereas, the levels in the right
region are assigned to the right extremity. Note also
that the levels in the middle region can be classified
later by the rule derived from the single variable.
The optimum correct classification rate by these
two-variable classification rules in addition to the
single rule is 0.76562, with
12
n =2 and
21
n =43. A
slightly better result is achieved than from the single
variable rule where the correct classification rate is
0.75521, with
12
n =0 and
21
n =47.
Figure 5: Biplot of variables A9 and D.
By examining the two misclassifications of
12
n ,
one finds an additional rule to eliminate
12
n : When
(A3=1, A4>=3, A6=3) then D=2. This means that
when the triage level is 1, the mental status is ‘to
pain’ or ‘coma’, and the diastolic blood pressure is
above 110 mm Hg (very serious high blood
pressure), the patient should not be administered
HCT because the situation is probably too dangerous.
This is a special provision under the rule of stating
that when (A3=1, A4>=3) then D=1, thereby
indicating the importance of abnormally high
diastolic blood pressure, a strong indicator to
overrule the HCT decision under serious health
conditions.
At this point, the correct classification rate is
0.77604, with
12
n =0 and
21
n =43. Note that
21
n
means the number of misclassified members,
thereby these members are treated as not
administering HCT (D=2) when in fact they need for
administering HCT (D=1). Misclassifying D=1 as
D=2 is more serious than that of D=2 as D=1 since
the penalty for the former error is life or death;
whereas, the consequence of the latter is merely a
waste of CT resource utilization. Note that of 192
patients only 48 patients were classified as D=1;
moreover, of these 48, the classification was correct
only five times. Since correct classification rate for
the 48 patients was very low, it is worthwhile to
investigate why
21
n cannot be reduced. By
examining the sorted data of
21
n =43, one notices
M
283
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE SEARCHING - Exemplieied by CT Data of Patient

that the age factor has been overlooked. When
considering the age factor (A2), a new rule is
formulated to reduce
21
n : when (A2=5, A3=1,
A6=3) then D=1. This means that when the patient’s
age is above 65 years, the triage level is 1, and the
diastolic blood pressure is above 110 mm Hg, the
patient should be administered HCT. When this rule
is applied in addition to the previous composite rules,
the correct classification rate is increased to 0.79167,
with
12
n =1 and
21
n =39. The result of
12
n =1 is an
exception to the previous rule. Apparently, nothing
can be done to further reduce the
21
n . The parallel
coordinate plot (PCP) of seven variables (A1-A7)
for the data of
21
n =39 is shown in Figure 6.
Figure 6: Parallel coordinate plots of 39 hospital data.
Several points are noteworthy. First, in comparison
with Figure B1, Figure 6 has only one colour (black)
since the data of
21
n =39 are members of D=1 only.
Second, there is no connection between variables A3
through A6, thereby, indicating that the levels of A4
and A5 are of single value. Indeed, A4=1 and A5=2,
thus indicating that patients having a clear mental
status and a normal breathing rate are easily
misclassified as not needing HCT, an understandable
error. Third, there are four age levels (2-5) instead of
the five in the original setting. Each age level is
connected with two triage levels except for age level
2 of which is connected to only triage level 2. In
comparison with the PCP in Figure B1, the pattern
in Figure 6 is quite different, wherein each age level
is connected to almost every triage level. Fourth, the
diastolic blood pressure is shown only for levels 2
and 3, thereby indicating that none of the patients
has normal blood pressure. Moreover, the pulse
levels are at 1-3, thus indicating that none of the
patients has an unusually high pulse rate (greater
than 120/min). Furthermore, there is no connection
between A6=2 and A7=1, thereby indicating that no
patient has blood pressure in the range of 80 to 110
mm Hg and a pulse rate lower than 60/min.
After a close examination of the sorted 39 data
sets, another rule is discovered: if (A2=5, A3=1,
A4=1) then (D=1). This rule indicates that when the
patient is very old (more than 65 years) and has a
triage level of 1 and a clear mental status, HCT
should be administered. This rule will reduce one
mistake in
21
n , thereby rendering the correct
classification rate of 0.79688 with
12
n =1 and
21
n =38, the optimum discoverable solution. The
PCP of the
21
n =38 data set is shown in Figure 7.
When comparing Figures 6 and 7, one notices that
the line connecting the normalized value of A2=1 to
A3=0 in Figure 6 has been deleted from Figure 7.
There is no observable distinction between D=1
from 38 patients and D=2 from 122 patients,
extracted from 144 data sets, wherein D=2 in the test
data has the response variable D=2 with A2>1 and
A4=1 and A5=2 and A6>1 and A7<4. The
aforementioned conditions set for D=2 are exactly
the same as for the 38 sets except for D=1. The PCP
of the 122 sets is shown in Figure 8. When
comparing Figures 7 and 8, it is clear that if the line
segments in each Figure are treated as elements in a
set, then Figure 7 can be regarded as contained in
Figure 8 in terms of the set concept, thereby
demonstrating that since the 38 sets are prominently
involved with the corresponding 122 sets, the two
cannot be separated by any rule. For the sake of
completeness, part of the XploRe (Hardle, Klinke
and Muller, 2000) code is listed to illustrate the
formulation of the composite rule in Appendix D.
The self-explanatory code is similar to the c code.
Figure 7: Parallel coordinate plots of 38 hospital data.
ICEIS 2008 - International Conference on Enterprise Information Systems
284

Figure 8: Parallel coordinate plots of 122 hospital data.
5 CONCLUSIONS
Two multivariate techniques have been proposed to
clarify patients sent to an emergency room to wait
for a decision on the administration of HCT. The
959 data set were segmented into two portions, a
767 training data set and a 192 test data set, after
which Fisher’s linear discriminant function was used
to find linear rule vector
a . Since classification
using rule vector
a in equation (4) is not practical
for on-duty physicians, three important variables,
such as triage (A3), mental status (A4) and breathing
rate (A5), were chosen on the basis of the magnitude
of the coefficients of
a . Next, correspondence
analysis was used to determine the simple
classification rule most suitable for each variable to
classify the need for administering HCT. The simple
classification rule has the format of (if A5=x then
D=y)where x and y are the levels of the input (A5)
and output (D) variables, respectively. The selection
of the rule is based on the shortest Euclidean
distance between the levels of the input variable
(e.g., A5) and response variable D located on the x-
axis of a biplot. The case study demonstrated that
output from the joint effort of the multivariate
technique coincided with the exhaustive search, a
promising result. The optimum correct rate is only
0.75521 with
12
n =0 and
21
n =47 for the rule of (if
A5=2 the D=2), meaning that if the patient’s
breathing rate lies within the normal range of
10~24/min, HCT is not needed.
The extension of a single-variable classification
rule to a two-variable one is straightforward, yet
requiring a small modification for choosing the rule.
First, a composite variable (e.g., A9) is formed by a
linear combination of the two variables based on
equation (10) so that each combination of the levels
from the two maps into an integer level of the
composite variable. Then typical CorrAna is applied
to the contingency table formed by variables A9 and
D, wherein a biplot is produced with points
representing both the levels of the composite
variable and response variable D. By taking the two
points of the levels of D as the demarcation points,
the x-axis can be cut into three regions: one to the
left of the left extremity, the second between the
demarcations, and the third to the right of the right
extremity. Moreover, the levels in the left regions
are assigned to the level of D at the left demarcation
point, the levels in the right regions to the level of D
at the right demarcation point, and the levels of the
composite variable between to the level of D on the
basis of the optimum classification rule from the
single variable. The two variables selected are triage
(A3) and mental status (A4), which render the
highest correct classification rate among all
combinations of two variables. The rules state that
when (A3=2 and A4=4) or (A3=1 and A4=3 or 4 or
2) D=1; whereas, when (A3=3 and A4=2) or (A3=3
and A4=1), D=2. Thus, the correct classification rate
is 0.76562 with
12
n =2 and
21
n =43.
The correct classification rate can be further
increased by examining the structure of the sorted
but misclassified items in the test data set. The
formulation of the composite rule for the case study
is listed in Appendix D, with the correct
classification rate of 0.79688 with
12
n =1 and
21
n =38. The composite rules may be generally
summarized as (1) when the triage level is 2 and the
mental status is a coma, or when the triage level is 1
and the mental status is unclear, HCT should be
administered, and (2) when the patient is in level 3
of triage and the mental status is one capable of
responding to a verbal stimulus, HCT is unnecessary.
Exceptional rules should be applied to patients older
than 65 years (A2) and those with high diastolic
blood pressure (A6). For example, (1) when the
triage level is 1, the mental status is ‘to pain’ or
‘coma’, and the diastolic blood pressure is above
110 mm Hg (seriously high), the patient should not
be administered HCT; (2) when the patient’s age is
older than 65 years, the triage level is 1, and the
diastolic blood pressure is above 110 mm Hg, the
patient must be administered HCT. It is noteworthy
that the variables of sex (A1) and pulse rate (A7) are
not considered in the composite rules.
M
285
MULTIVARIATE TECHNIQUE FOR CLASSIFICATION RULE SEARCHING - Exemplieied by CT Data of Patient

To show why the correct classification rate cannot
be increased, two parallel coordinate plots of
the
21
n =38 data set being in D=1 and the
corresponding 122 data set being in D=2 were
compared. The two data sets had the same domains
for variables A1-A7. The comparison indicated that
since both are prominently involved (highly similar),
they cannot be separated by any rule. Thus, no
improvement can be made in the correct
classification rate.
ACKNOWLEDGEMENTS
I grateful thank my colleague Prof. Paul Chen for
both encouraging me to pursue this research and
generally sharing his hospital data. I also express
appreciation to Dr. Cheryl Rutlede, Department of
English, DaYeh University, for her editorial
assistance.
REFERENCES
Yang, M., Kriegman, D and Ahuja, N., 2001, Face
Detection Using Multimodal Density Models,
Computer Vision and Image Understanding 84, 264–
284.
Lam, K. and Moy, J., 2003, A piecewise linear
programming approach to the two-group discriminant
problem
–
an adaptation to Fisher’s linear
discriminant function model, European Journal of
Operational Research 145, 471– 481.
Allombert, S., Gaston, A. and Martin, J., 2005, A natural
experiment on the impact of overabundant deer on
songbird populations, Biological Conservation 126,
1– 13.
Hardle, W. and Simar L., 2003. Applied Multivariate
Statistical Analysis, Springer. Berlin.
Johnson R. and Wichern D., 2002, Applied Multivariate
Statistical Analysis, Prentice Hall. 5
th
, NJ, USA.
Hardle, W., Klinke, S. and Muller M., 2000. XploRe
Learning Guide, Springer. Berlin.
ICEIS 2008 - International Conference on Enterprise Information Systems
286
